如何求出不规则图形的面积

丁雪洁

生活中常常需要估计各种不规则图形的面积，如何才能更好地求出不规则图形的面积？可以尝试用以下几种方法。

【方法一】选用合适单位，数方格估算面积

1.提出问题

教师出示一片真实的树叶，并提问：“你们能想办法求出这一叶片的面积吗？”

2.动手操作

教师为学生提供树叶剪贴片、大小为1 dm?和1 cm?的透明方格塑料片等工具，让学生选择合适的方法测量面积。

3.讨论交流

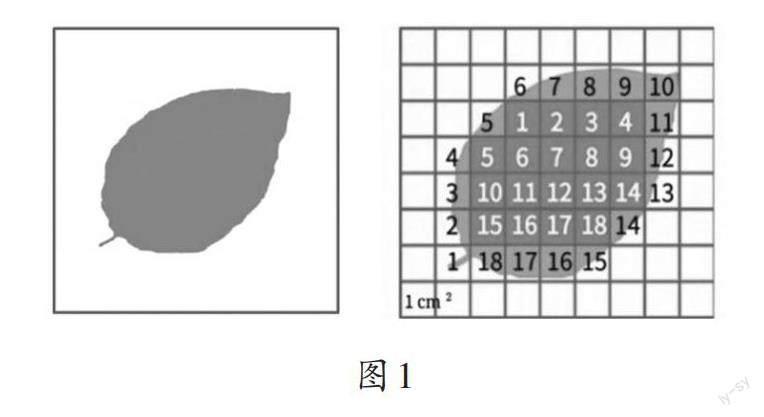
（1）为什么选择1 cm?的方格塑料片进行测量？（如图1）

（2）为什么大家得到的测量结果不同？

4.方法优化

先让学生汇报数方格的方法，然后全班讨论用什么方法比较合理。

（1）区间法：满格的有18格，即为18 cm?；包含图形的总格子有36格，即为36 cm?。叶片的面积在18 cm?至36 cm?之间。

（2）折中法：不满一格的均按半格算，有18个不满一格的格子，即为9 cm?，加上满格的18cm?，叶片的面积大约为27 cm?。

（3）舍小法：不满半格的有7格，舍去；满半格或超过半格的按一格算。叶片的面积大约为29 cm?。

（4）凑整法：超过半格和不满半格的可合并为一格，剩余接近半格的合一格，叶片的面积大约为28 cm?。

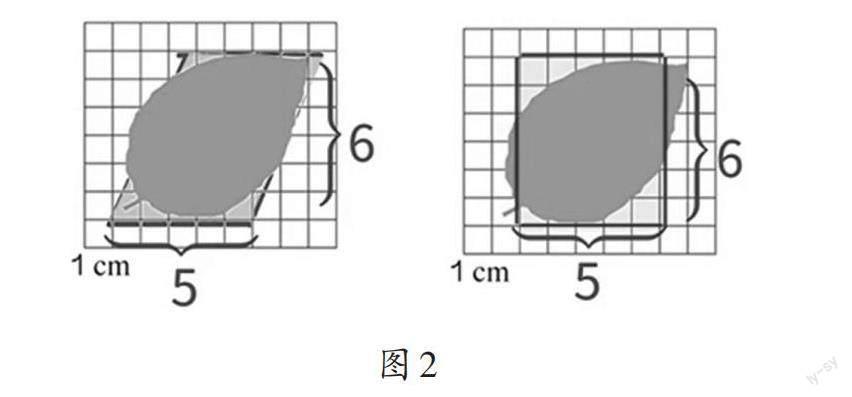
【方法二】运用化曲为直，用图形计算公式计算面积

1.想象转化

教师提问：“观察叶片，它最像我们学过的哪个图形？”

2.公式计算

根据平行四边形面积公式计算叶片的面积（如图2）。

3.讨论交流

还可以把叶片看成什么图形来计算面积？

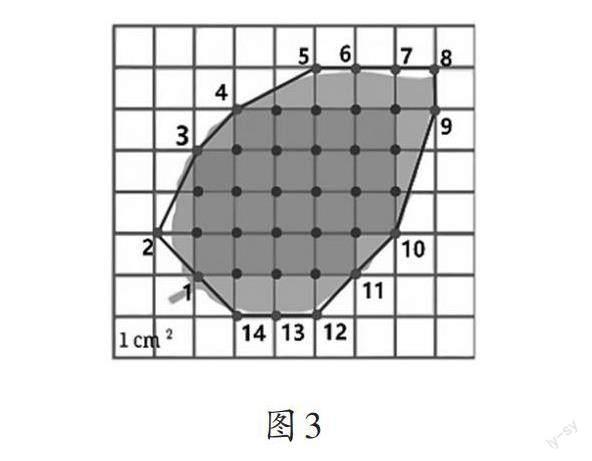
【方法三】活用皮克定理，用格点法计算面积

1.寻找格点

让学生在方格纸上摆放叶片，并描出外围格点（如图3）。

2.连接格点

引导学生将外围格点用线段连接起来，并数出边界（外围）格点数和图形内格点数。

3.公式计算

格点图形的面积=边界格点数÷2+内部格点数-1，即面积为14÷2+23-1=29（cm2）。

【方法四】巧用數学实验，用天平称量面积

1.引发讨论

教师提供天平、磁性纸板、剪刀等学习工具。请四人小组讨论：如何称出叶片的面积？

2. 头脑风暴

引导学生思考：已知1张面积为10 cm?的磁性纸板的质量，你能求出任意质量的磁性纸板的面积吗？让学生初步感悟“面积称量法”。

3.称量实验

（1）将10张磁性纸板叠在一起，在最上面的磁性纸板上描出叶片轮廓，剪下10张叶片大小的磁性纸板（下文简称“叶片纸板”）。

（2）用天平称出10张叶片纸板的质量。

（3）剪出10 cm?的磁性纸板并称出质量。

（4）根据“1张叶片的面积=10张叶片纸板的质量÷10张1 cm?（10 cm?）磁性纸板的质量”算出结果。

以上教学运用数方格、图形计算公式、格点计算、称量实验等方法求不规则图形的面积，不仅能提高学生解决实际问题的能力，还能培养学生的量感、推理意识和创新能力。

（安徽省淮北市第一实验小学）