学习材料多向关联 核心任务分层进阶

陈霞

【摘   要】单元复习课对学生构建系统的认知结构、发展数学思维能力起着重要的作用。在“表内乘法（二）”的单元复习中，教师结合教材分时段编排的特征，依据低年级学生的认知特点，通过“单元整体解读，聚焦本质关联；把握学情特征，多维材料提升；设置核心任务，思维分项进阶”的教学策略，促进学生综合素养的提升。

【关键词】核心内容；多向关联；分层进阶

“表内乘法（二）”是人教版教材二年级上册的学习内容。在学习这一内容之前，学生已经初步认识了乘法，会归纳乘法口诀，并熟练地掌握了2～6的乘法口诀，会用乘法口诀计算乘法。本单元内容既是前面已经学过的乘法口诀知识的拓展和延伸，也是后面学习表内除法和多位数乘除法的基础。通过单元复习课对本单元内容进行复习，不仅能帮助学生巩固已有知识，还能为后续的学习打下基础。

低年级单元复习课的内容基础性强，但知识点之间缺乏联系。为此，教师可基于低年级学生的认知特点，开发多向关联的学习材料，并通过设置核心任务，使学生实现数学思维的进阶。

一、单元整体解读，聚焦本质关联

设置单元核心任务需先提炼单元核心内容，从整体视角明晰复习单元的主题，把握单元中的核心内容及关键要素，梳理前面已经学过的知识和后续将要学习的相关知识。乘法是相同加数求和的简便运算。从同数连加到乘法算式的学习过程，可以“求几个几的和”为乘法概念及乘法口诀教学的核心内容，然后通过横向对应单元内容、纵向关联后续相关知识，明确单元复习的主题。

从横向看，由于乘法口诀的学习容量较大，故教材在编排时分为“表内乘法（一）”和“表内乘法（二）”两个单元进行教学：“表内乘法（一）”单元包含乘法的意义和2～6的乘法口诀，“表内乘法（二）”单元包含7～9的乘法口诀及解决简单的实际问题。复习“表内乘法（二）”单元时，要与“表内乘法（一）”单元的内容进行关联，以乘法意义为统领，兼顾2～6的乘法口诀，重点巩固7～9的乘法口诀。

从纵向看，在二年级的“表内乘法”和四年级的“乘法的意义”之间，教材还安排了“表内除法”“多位数乘一位数”“多位数乘两位数”等内容。其中，乘法口诀表压缩了乘法计算的过程，而对“乘法的意义”的理解则始终渗透在整个学习过程中。

小学阶段的数学运算结构主要是加法结构和乘法结构，而乘法结构是在加法结构的基础上产生的更高的认知结构。乘法结构的教学大致包括以下三类：每份数与份数相乘、“长×宽”的面积模型、“倍”的数学模型。这三类内容在教学中彼此独立，但数学本质是相同的。这也从另一方面说明，乘法意义的学习影响着学生对倍的认识和对长方形的面积的理解。

二、把握学情特征，多维材料提升

单元复习课的学习材料不仅要关联数学本质，还要关注学情及学生的认知特点。教师要在核心任务驱动下，选取简约、有整体性且具有多点结构、多向关联的学习材料。

（一）多关联学习材料促建构

前测题1：用“四六二十四”这句口诀能表示哪些选项？（提供文字描述、图式表示、连加算式、乘法算式、乘加乘减算式和实际问题6个选项）

从测试结果看，大多数学生选择“4个6相加”和“6个4相加”这类用文字描述的表征方式，而选择用乘加乘减或实际问题表征的人数占比较少。可见，学生的思维水平多数仅停留在“单点结构”水平。因此，单元复习课的重点应是帮助学生由“单点结构”水平走向“多点结构”水平，教学时须强调乘法的意义、乘法口诀、乘加乘减及用口诀解决实际问题等多向关联。

教师可以预设“口诀二八十六表示什么”“哪些问题可以用口诀三七二十一来解决”两类学习材料，串联沟通单元内容，以多形式进行关联，帮助学生形成认知结构，拓展知识内涵。教师要让学生在多元表征中，通过沟通、对比和抽象，概括出文字、算式、图式表征之间的本质联系，以多向关联的结构化材料，加深学生对乘法意义和口诀含义的理解，再现乘法口诀的建构过程。

（二）多维度学习材料促提升

易错点是单元复习课选择学习材料时的关注点之一。“数的运算”主题的单元复习须夯实用乘法口诀进行速算的能力，但不能平均用力，而是要重点关注45句口诀在学习和应用上的差异点，做到查漏补缺、熟练掌握技能。

在“表内乘法（二）”单元的学习中，学生容易混淆“七八五十六”和“六九五十四”、“七九六十三”和“八八六十四”等几组乘法口诀，即积较大且乘数比较接近的口诀。同时，学生在后续“用乘法口诀求商”时，计算“16÷8=2”的正确率要比“16÷2=8”的正确率高。这是因为人教版教材的乘法口诀按“小九九”编排，口诀“二八十六”编排在《8的乘法口诀》的教学内容中，所以16与8的关联程度要比16与2的关联程度高。因此，从学生的认知角度而言，教师应在“表内乘法（二）”的单元复习中引入“大九九”的乘法口诀表，完善学生的认知结构，凸显乘法口诀之间的关联。

基于此，教师设计了“大九九”乘法口诀表作为多维度学习材料，引导学生在规律的探索中，强化对乘法口诀的理解，寻找乘法口诀之间的关系，熟练掌握用口诀求积。再将乘法口诀转化成81个方格图，通过图式互译渗透乘法口诀与面积模型之间的联系。这样的学习材料新颖有趣，既能减少乘法口诀记忆的枯燥，又能加深学生对乘法的意义的理解。

三、设置核心任务，思维分项进阶

根据教材解读和学情分析的结果，核心任务的设计要围绕单元核心内容展开，并以此为教学主线，引导学生深度学习。核心任务既可以是一组分层递进的任务群，也可以是任务反馈中的分层推进，旨在引发学生的主动思考与自主建构，发展学生的数学思维。

（一）多元表征，意义关联

教师出示口诀“二八十六”。

◇任務一：请你画一画或写一写，尽可能多地表示这句乘法口诀的含义。

在教学反馈中，教师先呈现实物图式和加法算式，通过横向和纵向观察对比，得到2个8相加、8个2相加的意义。接着抽象成乘法算式2×8=16或8×2=16，复习乘法算式中各部分的名称。最后鼓励学生创编一个可以用“2×8=16”解决的实际问题（如图1）。

这样的任务设计引入了多向关联的结构化材料，加深了学生对乘法的意义和乘法口诀含义的理解，再现了乘法口诀的建构过程。

（二）完善认知，查漏补缺

教师出示“9×9”的方格表，要求学生将算式2×8=16填入相应位置。

◇任务二：填补乘法表，思考下列问题。

（1）算式2×8=16上下左右的方格中分别填什么乘法算式？这些乘法算式与2×8=16有什么关系？

（2）填一填与2×8=16同一横行和同一竖列的乘法算式（如图2），你发现了什么？

（3）快速填写其他乘法算式。想一想，可能会在哪些乘法算式的口诀上出错？

上述任务引导学生在分层完善“大九九”乘法表的过程中复习乘法口诀，认识相邻乘法口诀之间的关系，寻找容易混淆的口诀，拓展乘法的意义。

（三）任务进阶，以形解数

教师出示“大九九”乘法表，让学生结合图形的特征背诵乘法口诀，理解乘法的意义，通过乘法口诀与图式表征之间的互相转化，分项推进教学，渗透面积模型的含义，实现学生数学思维的进阶。

◇任务三：根据图中的乘法算式，你想到了什么乘法口诀？

子任务1：结合“大九九”乘法表复习乘法口诀的含义。

（1）教师在九九乘法表中呈现一个大长方形（如图3），提出问题：“根据这个长方形能够列出哪几道乘法算式？”引导学生通过观察得到“2个7相加”或“7个2相加”，对应乘法口诀“二七十四”，列出乘法算式2×7=14和7×2=14。再依次呈现多个不同的长方形，强调图、算式和口诀的对应。

（2）教师呈现三个相同大小的长方形（如图4），引导学生一组一组地观察，得到“3个9是27”，用乘法口诀“三九二十七”表示。

（3）教师呈现几组数量相同、形状不同的图形（如图5），引导学生寻找对应的乘法口诀，得出这几组图形可以用乘法口诀“三九二十七”表示。

上述任务引导学生通过看图找乘法口诀，说乘法口诀想象图，建立“图”和“式”的关系。教师使用的学习材料从一个长方形图进阶到多组相同的长方形图，再到多组不规则图形，引导学生从“一个一个数”发展到“一群一群数”，对乘法口诀建构新的认识。

子任务2：利用图形变式拓展乘法的意义。

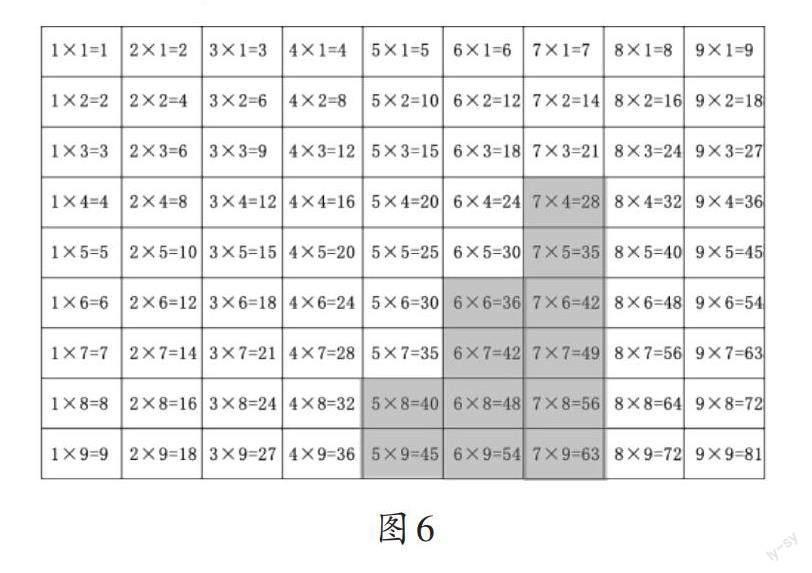
（1）教师依次呈现数量是2个、4个和6个等差摆放的组合图形（如图6），引导学生思考这些图形如何用乘法口诀来表示，从而将移多补少的方法应用于同数连加，使学生对乘法的意义的理解更深入。

（2）教师呈现有重叠的组合图形（如图7），让学生尝试用乘法口诀进行表示，引发学生的认知冲突，引导学生根据图形特点，从重叠部分入手进行思考，得到可以用2×9-1或2×8+1来表示，从而理解乘加和乘减的运算顺序和本质意义。

子任务3：结合算式特点经历“大九九”乘法表的简化过程。

（1）教师以问题“为什么我们学习的乘法口诀表没有81句呢”为引领，引导学生发现有两个乘法算式对应同一句口诀，如计算5×7和7×5这两个乘法算式都用到了“五七三十五”这句口诀，所以将两个算式合并，呈现对应的乘法口诀。依次类推，让学生经历将“大九九”乘法口诀表简化成“小九九”乘法口诀表的过程（如图8）。

（2）为进一步引导学生理解同数相乘的算式，理解为什么这些乘法口诀只能对应一个乘法算式，教师借助面积模型对这些同数相乘的口诀和算式进行表征，引导学生发现对应的图形正好是正方形，从而渗透正方形边的特征及面积计算的特殊性（如圖9）。

（四）分层反馈，突破难点

乘法运算的意义是解决问题的基础。依据乘法运算意义解决现实情境中的问题，可以帮助学生更好地寻找数量关系，发展学生解决问题的能力。

◇任务四：运用乘法口诀“三七二十一”解决问题。

教师呈现6个现实情境问题（如图10），让学生判断这些问题是否可以用乘法口诀“三七二十一”解决。反馈时，教师需要按照学生的认知循序推进。

（1）区别加法模型与乘法模型。对比①和②，让学生结合图式理解“（    ）和（    ）相加”与“（    ）个（    ）相加”的不同意义，借助直观图式查漏补缺，帮助学生建构系统化的知识体系。

（2）在计算⑥号问题时，引导学生借助移多补少的方法，用口诀“四七二十八”计算出2019年2月一共有28天，积累生活经验。

（3）沟通④号算式3×6+3和算式3×7，帮助学生理解乘法算式和乘加、乘减算式两者关联的本质是乘法的意义；基于此，在解决⑤号问题时，引导学生从不同的角度思考，选择3×8-3、3×6+3和3×7等算式解决问题。

（4）反馈⑤号问题，将乘法口诀与生活情境建立联系，引导学生创造性地解决问题，发展学生的高阶思维。

总之，单元复习课的教学设计需要凸显以学为本，关注学生的知识基础与学习能力，关注学生对学习内容的深层次理解，重视完善学生的认知结构，促进学生形成数学思维，发展学生的核心素养。

参考文献：

［1］邵汉民，钱亚芳，陈芳.小学数学整体设计的思与行：小学乘法教学［M］.上海：上海教育出版社，2022.

［2］张优幼.关注“粗心”背后的事实：“用乘法口诀求商”的后测和前测［J］.中小学数学（小学版），2010（1/2）：12-13.

［3］刘丽娟.经历过程   自主建构：二年级上册“表内乘法”教材解析与教学建议［J］.小学数学教育，2015（7/8）：28-32.

［4］肖淑芬.丰富复习课功能，始于教学目标的全面定位［J］.小学教学研究，2012（1）：45-47.

（浙江省台州市椒江区中山小学杨司校区）