基于稀疏表示的数据无失真压缩模型构建

孙壮

（曲阜师范大学，山东济宁 272000）

在数据分析研究过程中，数据压缩是一个基础问题。一方面，数据压缩能够减小存储空间，降低传输成本；另一方面，数据压缩可以降低数据挖掘复杂度，并且可以保障数据内容的完整性与精确性。在常规的数据应用场景中，通信传输容量存在限制，对原始数据进行压缩是保障有效传输的关键手段之一[1-2]。数据压缩需要满足下述需求：一是保留原始数据局部、全局特征，并可以通过某种手段还原原始数据；二是数据压缩运算不能够过于繁琐、复杂，保障压缩、解压与随机访问速度。就现有研究成果来看，已有数据压缩模型由于应用方法自身缺陷，致使压缩后数据容易出现失真现象，影响原始数据的精确性，故提出基于稀疏表示的数据无失真压缩模型构建方法。

1 数据无失真压缩模型构建研究

1.1 数据稀疏表示

为了避免数据压缩出现失真现象，基于超完备字典学习方法稀疏表示数据，简化数据的结构，为后续数据缺失填补奠定坚实的基础。

超完备字典学习方法主要应用于数据稀疏表示基函数获取阶段，通过系数与稀疏表示基函数使得原始数据特征不改变[3]。设定超完备字典为L∈Rm×n，数据样本集合为，其对应的稀疏表示系数向量集合为。其中，m为数据样本总数量，n为稀疏表示系数总数量，则超完备字典学习原理表达式为：

以式（1）确定的超完备字典学习过程为基础，制定超完备字典学习[4-5]具体步骤，具体如下所示：

步骤1：超完备字典初始化。基于给定的过完备字典或者数据样本对字典进行初始化处理；

步骤2：稀疏编码。以步骤1 初始化后的字典L为基础，基于正交匹配追踪算法求解每一个数据样本ai对应的稀疏系数向量bi。

步骤3：超完备字典更新。以步骤2 计算的稀疏系数向量bi为依据，对超完备字典L进行更新处理。依据上述步骤对L中所有原子进行逐列更新，从而产生新的超完备字典。

步骤4：数据稀疏表示。将采集的数据y输入至更新后的超完备字典中，获取稀疏系数[6]向量{b1,b2,…,bi,…,bn}，则数据稀疏表示为：

根据上述过程完成数据的稀疏表示，并制定超完备字典的更新方式，以此来保障稀疏系数向量获取的精准度，为最终数据压缩的实现提供便利。

1.2 数据聚类处理

以稀疏表示后的数据为基础，计算数据之间的相似度，应用谱聚类算法[7-8]聚类数据，以此降低数据压缩的运算量。

采用自身乘以自身转置的方式，将数据稀疏系数向量转化为n×n方阵，以此为基础，计算任意两个数据yi与yj之间的相似度函数，表达式为：

式中，ηij为数据yi与yj之间的相似度函数；为稀疏系数方阵的相似权重。

以谱聚类算法为手段，获取ηij对应的对角矩阵U与拉普拉斯矩阵V[9-10]，对拉普拉斯矩阵V进行求解，获取多个特征向量，并对其进行降序排列，通过标准化处理，获得向量S=[s1,s2,…,sk]，sk代表第k个拉普拉斯矩阵V特征向量[11-12]。以向量S的行向量si为聚类中心，以数据与聚类中心si之间的欧氏距离为依据，划分数据类别，具体规则如下式所示：

式中，dij为聚类中心si与数据yj的欧氏距离；γ′为欧氏距离的辅助计算参数；ε0为误差项；d*为聚类欧氏距离阈值。当dij≤d*时，将数据归到ci类；当dij>d*时，将数据归到其他类。

依据上述规则遍历全部数据，直至聚类结束为止，获得数据聚类结果为{c1,c2,…,cp}，为最终的数据压缩提供依据。

1.3 数据缺失填补

在数据稀疏表示与聚类处理过程中，容易出现数据丢失现象，造成数据缺失，影响数据的最终压缩与应用。因此，此研究应用SoftImpute 算法[13]填补缺失数据，为后续无失真压缩的实现做好准备。

数据缺失填补程序如图1 所示。

如图1 所示，采用Lasso 优化求解来估计缺失数据，表达式为：

将式（5）估计的缺失数据填补到数据缺失位置，即可完成数据的缺失填补，为数据的完整性提供保障。

1.4 数据无失真压缩

以缺失填补后的数据聚类集合C={c1,c2,…,cp}为基础，应用k-means 算法[16]对数据进行无失真压缩，为数据的应用提供便利。

基于PredZip 算法的数据无失真压缩框架如图2所示。

图2 数据无失真压缩框架图

数据无失真压缩主要划分为两个阶段，分别为算术编码阶段与概率预测阶段。对数据进行独立编码，编码后数据向量只有一个维度的值为1，其余值均为0，例如00000001、01000000 等。概率预测阶段主要是对数据概率分布数值进行预测，以此来保障压缩数据的准确性。

上述过程实现了数据的无失真压缩，节省了存储空间，为管理人员提供更简便的数据支撑。

2 实验与结果分析

选取基于分布式压缩感知和边缘计算的配电网电能质量数据压缩存储方法与基于变形场测量数据主元压缩的模型参量反求方法作为对比模型，设计数据无失真压缩对比实验，以此来验证构建模型数据压缩性能。

2.1 实验数据准备

选取某公司财务管理系统财务数据作为实验对象，由于财务数据体量较大，若直接对其进行应用，会造成实验过程较长，运算量过大等缺陷，也会导致实验结论的偏差。因此，在公司财务管理系统中随机选取1 100 MB 财务数据作为实验数据，将其随机划分为10 个实验组别，为后续实验的进行提供便利。实验组别如表1 所示。

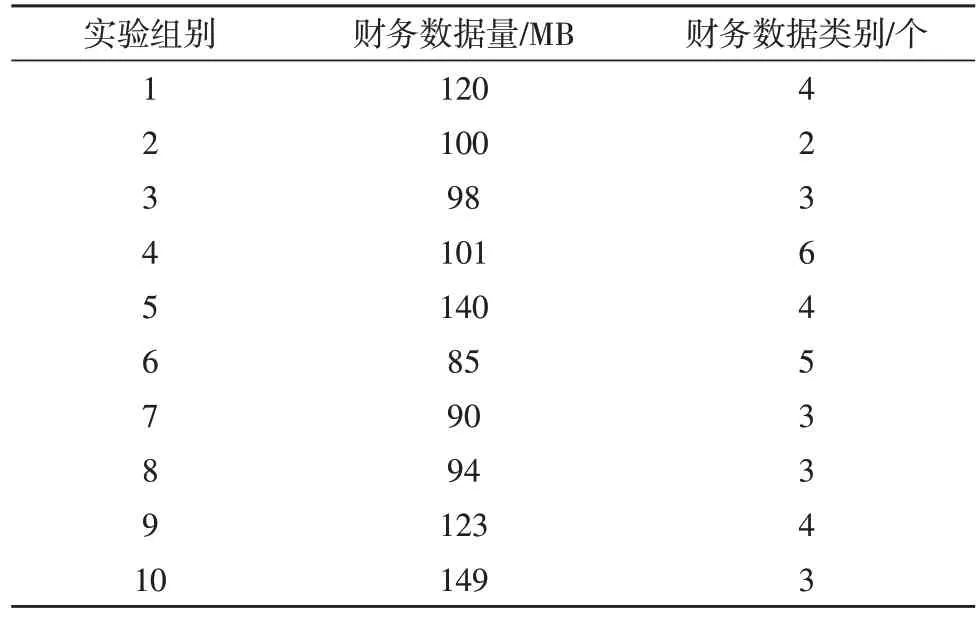
表1 实验组别

如表1 所示，划分的10 个实验组别中，财务数据量与财务数据类别具有较大的差别，表明每个组别的实验工况存在一定的差异，符合数据压缩模型应用性能测试需求。

2.2 评价指标选取

为了直观显示构建模型的应用性能，选取压缩增益、压缩比与压缩失真率作为评价指标进行测试。常规情况下，压缩增益数值越大，压缩比与压缩失真率数值越小，表明数据压缩性能越好；反之，压缩增益数值越小，压缩比与压缩失真率数值越大，表明数据压缩性能越差。

2.3 实验结果分析

以上述准备的实验数据选取的评价指标为基础，进行财务数据压缩实验，记录实验数据，计算评价指标数值，具体如图3 所示。

图3 评价指标数据图

如图3(a)数据所示，相较于两种对比模型，应用构建模型获得的财务数据压缩增益数值更大，最大值为18.8；如图3(b)数据所示，相较于两种对比模型，应用构建模型获得的财务数据压缩比数值更小，最小值为0.1；如图3(c)数据所示，相较于两种对比模型，应用构建模型获得的财务数据压缩失真率数值更小，最小值为0.5%，充分证实了构建模型数据压缩性能更佳。

3 结束语

财务数据是企业运营管理的主要依据，也是重要决策制定的关键因素。但是，随着信息化水平的提升，企业财务数据数量呈现暴增趋势，为财务数据存储、应用带来了极大的挑战。很多企业由于存储空间不足，删除较为久远的财务数据，待需要时无从取证。由此可见，如何对财务数据进行无失真压缩处理是保障企业可持续发展的关键手段，故提出基于稀疏表示的数据无失真压缩模型构建研究。实验数据表明，构建模型大幅度提升了数据压缩增益，降低了数据压缩比与压缩失真率，能够为财务数据处理提供更有效的模型支撑，也为相关研究提供一定的借鉴。