变刚度层压板的轨迹规划算法研究

方宜武，于鹏飞，徐庶，田琪，谢文雅，王忠

（中国电子科技南湖研究院 先进算法实验室，浙江嘉兴 314001）

0 引言

在复合材料自动铺丝和/或连续纤维3D打印中，可实现单向纤维的曲线铺放，使铺放角度在同一铺层之内连续变化，从而提高可设计性，使增强结构性能或减轻结构质量成为可能[1-3]。带有连续变化纤维角度铺层的复合材料被称为变刚度复合材料层压板（Variable Stiffness Composite Laminates）[4-5]，不断变化的纤维取向使每层的刚度在不同空间位置各不相同。设计者借此调整层压板内在载荷分布，提高结构有效性[5-6]。Waldhart[1]对变刚度层压板进行了理论与仿真分析，Kim等[2]完成对连续纤维复合材料层压板的制造与验证，Lopes等[3]验证了变刚度层压板在压缩屈曲和首层破坏模式下的性能优势，Gürdal[5-6]等将变角度铺层应用到实际中，杨竣博[7]完成了对变角度层压板参数化定义并研究其在不同轴压载荷下的力学性能，但所有这些研究中涉及到变刚度层压板具体轨迹规划算法的不多。

基于上述研究背景，首先定义变角度铺层的基准参考路径，然后通过“移动”基准参考路径得到其他路径，进而得到整个变角度铺层纤维角度的变化规律。基准轨迹的描述形式有很多种，线性函数法因其最具代表性和简洁性而被广泛采用[7]，其他路径可通过平移动轨迹和平行轨迹获得[1]。本文采用线性函数法描述基准轨迹，采用平移动轨迹和平行移动轨迹得到剩余轨迹，并分别得到各自的算法，该算法可扩展应用至任意变化角度。

1 变角度轨迹算法

1.1 变角度基准轨迹描述

变角度层压板的轨迹示意如图1所示。若用线性函数Y=F（X）=φ〈T0|T1〉表示旋转坐标系XOY中的纤维角度变化规律[1]，由旋转坐标轴的性质，纤维轨迹在坐标系xoy中的线性表达式为：

图1 变角度轨迹示意图

轨迹上的点P（x, y）处轨迹方向与x轴的夹角公式为

式（1）、式（2）中X= x·cos φ+y·sin φ。

1.2 变角度基准轨迹算法

复杂三维外形的零件CAD可通过网格化处理进行编程计算[8-9]，对于二维平板，仅通过沿x方向的步长λ便可描述轨迹点Pi（xi，yi）和它的上一轨迹点Pi-1（xi-1，yi-1）的关系。如图2所示，铺放起始点P0坐标和起始铺放方向v0已知，用θ（xi，yi）表示点Pi（xi，yi）处铺放（轨迹）方向与x轴的夹角，简记为θi。用Δθi表示点Pi（xi，yi）处相对于上一铺放点Pi-1（xi-1，yi-1）的偏转角度若给定各轨迹点间的步长λi，可求出系列铺放点{P0，P1，P2，…，Pi-1，Pi}的坐标：

图2 基准轨迹算法示意图

对于采用步长λi计算的轨迹规划而言，特别是轨迹曲率变化较大时，步长划分的结果决定了算法的精度和效率。即轨迹线曲率改变较大时，铺丝头旋转角度变化大，为保证轨迹线的精准度并防止因铺丝头旋转过大而引起纤维拉伸，步长应较小。理想轨迹点的疏密程度应与其曲率变化程度正相关，这就要求步长大小与曲线曲率变化程度负相关。

如图2所示，当轨迹点取至点Pi（xi，yi）并求取下一轨迹点。

步骤1：利用式（2）计算点Pi处的轨迹角度θi；

步骤2：输入步长λi，利用式（3）计算点Pi+1坐标（xi+1，yi+1）；

步骤3：按前2步求取下一轨迹点Pi+2，直至模型边界。

1.3 平移轨迹算法

平行轨迹算法即将基准铺放轨迹沿某一方向移动一定距离得到其相邻的铺放轨迹，以图3为例将轨迹线{P0，P1，P2，…，Pi-1，Pi}沿与x轴夹角为α方向移动全丝束宽度w，得到轨迹线{Q0，Q1，Q2，…，Qi-1，Qi}；令di=PiQi=（xQi-xi，yQi-yi），使得di×vi恒正或恒负，可保证每次平移方向的一致性。平移轨迹点Qi（xQi，yQi）的求解方程见式（4）：

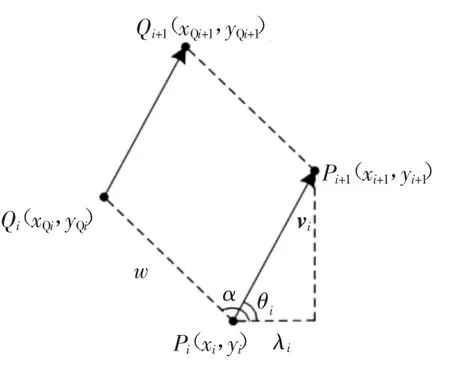
图3 平行轨迹算法示意图

得到轨迹线{Q0，Q1，Q2，…，Qi-1，Qi}后，按照上述方法将其沿某一方向平移，得到剩余的系列平移轨迹线覆满铺放面。

如图3所示，当轨迹点取至点Pi（xi，yi）时，平移轨迹求取过程如下。

步骤1：利用式（4）计算点Qi的坐标；

步骤2：至下一点Pi+1处按第1步利用式（4）计算点Qi+1的坐标，直至模型边界。

1.4 平行轨迹算法

以图4为例，将基准轨迹上的轨迹点{P0，P1，P2，…，Pi-1，Pi}各自沿其法线方向{n0，n1，n2，…，ni-1，ni}移动全丝束带宽w，得到系列轨迹点{Q0，Q1，Q2，…，Qi-1，Qi}，通过拟合这些轨迹点得到平行于基准轨迹的铺放轨迹线。以Ni表示垂直于轨迹Pi处轨迹线vi的方向，则轨迹Pi处的法线方向为ni=Ni+Ni-1；令di=PiQi=（xQi-xi，yQi-yi），使得di×vi恒正或恒负，可保证每次求取平行轨迹点方向的一致性。轨迹点Qi（xQi，yQi）的求解方程见式（5）：

图4 平行轨迹算法示意图

得到第一条平行轨迹线后，按照上述方法将其各铺放点沿其铺放方向的法线方向移动，得到下一条轨迹的铺放点并拟合得到其他平行轨迹线，直至覆满铺放面。

如图4所示，当轨迹点取至点Pi（xi，yi）时，平行轨迹求取过程如下：

步骤1：计算点Pi-1处的轨迹方向vi-1、点Pi处的轨迹方向vi；

步骤2：计算轨迹方向vi-1、vi的法向向量Ni-1、Ni；

步骤3：利用式（5）计算点Qi的坐标；

步骤4：按前3步在下一轨迹点Pi+1处求取其对应的平行轨迹点Qi+1，直至模型边界。

1.5 任意角度变化的轨迹点算法

在变刚度层压板铺放中，如图5所示，对已求解出上一轨迹点（或给定铺放起始点）Pi-1以及铺放至上一轨迹点的方向（或起始铺放方向）vi-1，当在下一轨迹点偏转任意角度Δθi时，轨迹点Pi的求解方程为：

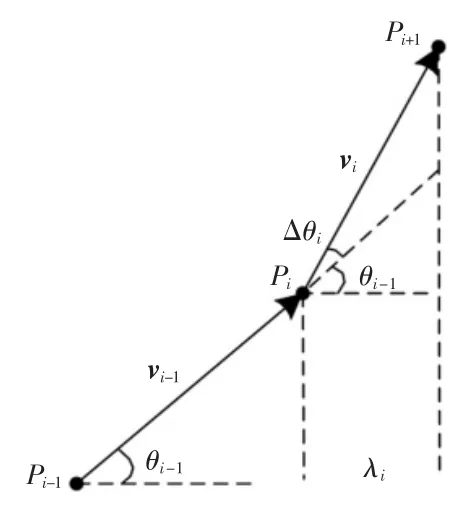
图5 变化任意角度的轨迹点算法示意图

任意变化角度的轨迹点求取过程如下：

步骤1：计算点Pi-1处的轨迹方向vi-1、输入步长λi和预设的偏转角度Δθi；

步骤2：利用式（5）计算点Pi的坐标；

步骤3：按前2步求解下一轨迹点Pi+1直至模型边界。

2 算法实现与实际样件试验验证

2.1 算法实现

为实现变刚度层压板算法，基于VC++平台开发了算法程序，算法以600 mm×600 mm平板为例，分别对0〈0|15〉基准线及其平移轨迹和平行轨迹、任意变角度轨迹及其平移轨迹和平行轨迹进行计算，将所得轨迹点导入三维建模软件CATIA并插值绘制其轨迹线，结果如图6、图7所示。从图6、图7可以看出，轨迹线符合理论公式的计算，表明本文上述算法的正确性和合理性。

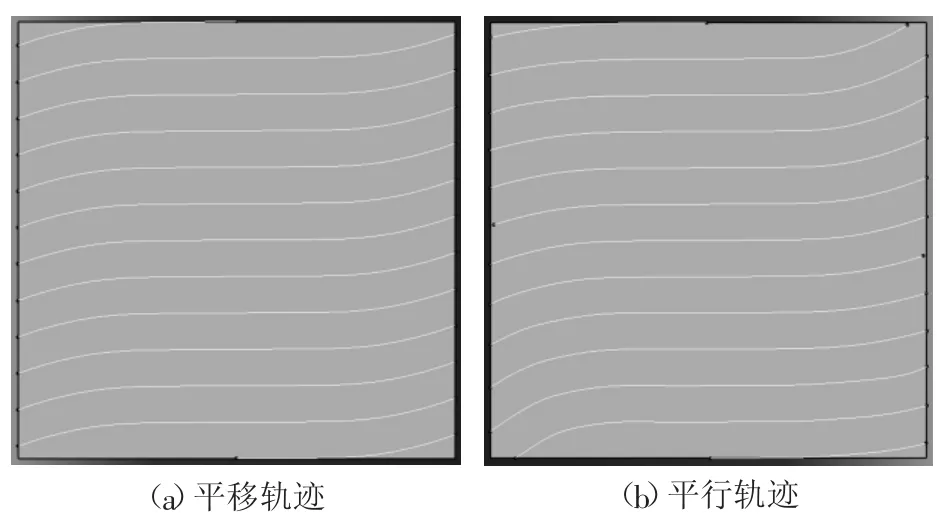
图6 0〈0|15〉基准轨迹的平移轨迹和平行轨迹

图7 任意基准轨迹的平移轨迹和平行轨迹

2.2 实际样件试验验证

为了验证试验实际效果，对无人机机身复杂连接结构进行连续纤维3D打印完成试验验证，效果如图8所示。由此可见，基准轨迹、平移轨迹和平行轨迹对应的连续纤维分布合理，验证了算法的实际应用可行性。

图8 无人机机身结构3D打印验证

3 结语

1）根据变角度轨迹的曲率变化设定步长，保证算法的精准度和效率；

2）提出变刚度层压板中变角度轨迹线性函数的基准轨迹、平移轨迹和平行轨迹，以及变化任意角度轨迹规划算法的数学原理，求解其变角度轨迹；

3）基于VC++平台编程实现算法，并按求解结果绘制轨迹线，验证了变角度算法的正确性和合理性，简化了编程难度、提高了计算效率，可作为变刚度层压板的模拟、编程、制造及其工程应用的技术支撑；

4）对无人机机身复杂连接结构进行连续纤维3D打印完成试验验证，完成对基准轨迹、平移轨迹和平行轨迹对应的连续纤维打印，分布合理，验证了算法的实际应用可行性。