某对数周期天线的橡胶阻尼减振优化分析与应用

阳丁，黄福清，尹本浩

（中国电子科技集团公司第二十九研究所，成都 610036）

0 引言

对数周期天线是由多个平行排列的对称振子按照结构周期率构成[1]，通常为悬臂结构，整体耐振动能力较差。解决对数周期天线振动安全性问题的基本手段无非有两种：一是加强对数周期天线结构的强度设计[2]；二是为对数周期天线添加减振措施。本文通过第二种方式解决对数周期天线的振动安全性问题。

减振技术已经大量应用于工程实践，根据是否需要外部能量输入可简单分为被动减振和主动减振，本文研究的橡胶阻尼减振技术属于被动减振。通常为振动敏感的对象添加减振器来实现被动减振。减振器通常具有储能和耗能两个部分功能，其中储能部分功能主要由减振器的刚度特性来体现，耗能部分功能主要由减振器的阻尼特性来体现。减振设计的主要工作便是为需要减振的对象匹配刚度合适、阻尼性能优越的减振器。

阻尼是振动系统耗能能力的体现，是材料或结构在承受周期应变时以热量方式消耗机械能的本领，其在振动系统中能有效地将振动幅值逐渐减小，起到抑制振动、降低噪声，以及避免系统因振动而产生结构疲劳损坏失效等作用[3]。按照阻尼产生的机理，阻尼通常可分为黏弹性阻尼、结构阻尼、流体阻尼和其他阻尼。为研究阻尼特性，针对不同阻尼，对应有相应的理论阻尼模型。本文涉及到的橡胶材料是常见的黏弹性阻尼材料，用黏弹性阻尼模型表示较为准确，如果较少考虑材料的温变特性和频变特性，也可用结构阻尼中的材料阻尼模型近似代替。

橡胶阻尼减振技术已经在航空航天、造船行业、汽车行业等有着较大范围的应用[4]。橡胶阻尼减振相关的力学模型研究日益深化[5]，其模型参数实验确认技术日渐成熟[6]，其工程数值仿真模拟与应用也愈加精确[7]。

可用于橡胶阻尼减振仿真计算的流行CAE软件主要有：NASTRN、ADINA、ANSYS、SAP2000等。ANSYS是一款功能强大、计算方便、图文输出、数据准确的有限元分析软件，其在推出Workbench平台后，为生产一线的工程师提供了更加人性化和高效的数值仿真计算环境。本文采用ANSYS软件进行计算，考虑的正是其工程实践上手容易。

目前，针对橡胶阻尼减振技术在电子技术领域的应用通常集中在数值模型的准确性研究、数值模型的温变和频变特性的拟合特性研究、不同阻尼数值模型的适应性研究等较为理论的问题研究上。对于一线工程师，需要解决大量的实际工程问题，需要的是对工程问题能有效处理的理论和简洁表达方法、大型实际模型的流程化仿真与验证、仿真与实物验证的对比及相互修正等。本文正是借助对某对数周期天线的橡胶阻尼减振优化分析与应用实践，逐步剖析该过程的一些重点问题。

1 某对数周期天线结构及振动问题

某对数周期天线结构如图1所示，该天线主要由馈电电缆、馈电后臂、振子片、底板、射频头、转接架、对外安装板、紧固件及加固件组成。天线主体安装到转接架上，最终通过对外安装板边沿的10个通孔安装到外部系统上。从图1中还可看到，天线结构类似于一个悬臂结构，受限于电气性能、对外装机条件和质量因素，该天线本体的结构进一步加强较为困难。

图1 某对数周期天线构成图

该天线通过周边孔安装到振动台面上做扫频耐久振动实验，振动的实验图谱如图2所示，实验等级：C级，实验方向：X、Y、Z三个轴向，实验时间：15 min循环1次，循环8次。该天线在实验过程中发生故障，故障点如图3中红圈所示，断裂主要发生在馈电电缆与馈电后臂的连接点、馈电电缆壳体、振子片的中部和振子片底部。

图2 振动实验图谱

图3 断裂故障点

2 问题描述涉及到的基本原理

2.1 振动基本原理及阻尼简介

通常涉及到的振动问题皆为多自由度振动问题，其控制方程如式（1），所有振动问题都集中在求解此控制方程上[8]。

式中：M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，x为位移向量，F为激励向量。

假设阻尼矩阵可以解耦成质量矩阵与刚度矩阵的组合，式（1）的求解便可转化为求解式（1）的特征值方程和求解特殊解问题，即将该振动系统假设为线性系统进行求解。通常激励向量中的单个激励力可通过傅里叶变换，分解为多个正弦激励的线性组合，式（1）的特征解通常可表示为

式中：xi为i自由度位移，Ai为i自由度幅值，ω为频率，φ为相角。

多自由度振动系统对应有多阶模态自然频率ω，设ωi及A（i）分别表示多自由度系统的第i个模态自然频率和模态向量，它们满足系统特征值方程：

把原始碳布进行适当的电化学处理，有效的改变了碳布表面的官能团，将其从疏水性变成亲水性，并增加了碳布表面的粗糙程度，进而增强了活性材料与导电碳布集流体之间的界面作用力。导电碳布将活性材料进行了有效分散，保证了活性材料的导电性，又防止其颗粒的逐渐长大。组装成的超级电容器不但具有柔性的功能，而且具有高的功率密度，可以点亮LED灯3 min。该工作发表在能源材料领域的国际顶级学术期刊Advanced Energy Materials 上[20]。

式中：k为正则化处理后的刚度矩阵，m为正则化处理后的质量矩阵。

系统的特征值问题可综合成：

式中，A为正则化模态矩阵，由正则化模态向量组成。

所有类型的阻尼反映在控制方程式（1）中的阻尼矩阵C中，通常橡胶材料的阻尼性能由其材料阻尼性能决定。在黏弹性阻尼情况下，材料的耗损因子等于材料阻尼比的2倍[3]，通常给定的是材料的耗损因子，在应用于有限元计算时，可据此计算得到对应的材料阻尼比。

2.2 振动图谱转化为有限元分析边界条件

图2所示的双振幅正弦振动图谱需要转化为有限元分析中的边界条件。由第1节内容可知，天线通过10个通孔对外安装，则可以用这10个通孔作为边界，按照图谱添加对应的位移激励。正弦振动的响应加速度可通过式（2）求导得到：

式中，f为频率。

通过式（5）可计算得到图2振动图谱中2000 Hz处振幅大小为8.7×10-4mm。图谱中双振幅值除以2得到对应的正弦振动幅值。

2.3 ANSYS阻尼表达及适用分析

ANSYS动力学分析中可以指定五种形式的阻尼：瑞利阻尼、和材料相关的阻尼、恒定的阻尼比、振型阻尼和单元阻尼。可以在分析中指定多种形式的阻尼，ANSYS按所指定的阻尼之和形成阻尼矩阵C。

在ANSYS动力学计算过程中，采用完全法和模态叠加法定义的阻尼不同，其中完全法使用的是节点坐标，模态叠加法使用的是总体坐标（如式（3）所示正则化坐标）。特别地，在模态叠加法中，每个模态产生有效阻尼比，而不像完全法计算整个阻尼矩阵C。

式中：α为常值质量阻尼，β为常值刚度阻尼，ξ为常值阻尼比为第i个模态的常值阻尼比，ξj为第j个材料的阻尼系数。

式中：Nm为模态总阶数为第j个材料的应变能，kj为第j个材料的刚度矩阵。

ANSYS动力学分析采用完全法时，某个材料阻尼代表了该材料的一个刚度矩阵乘子，类似于瑞利阻尼中的BETAD系数，而在模态叠加法中材料阻尼类似于与频率无关的常值阻尼，使用式（7）和式（8）来计算系统的每个模态的常值阻尼比。因此，在以模态叠加法为基础的谐响应分析、瞬态分析和谱分析中任何阻尼均会转换为模态的常值阻尼比，而忽略掉每种特殊阻尼对系统的独立作用。因此涉及到对数周期天线正弦扫频响应分析时，如要考虑橡胶减振器的材料阻尼的影响，就必须采用完全法。如在ANSYS软件模态叠加法中添加材料阻尼参与计算，系统便会弹出警告：材料阻尼已被忽略。

3 某对数周期天线的减振优化

3.1 对数周期天线振动仿真分析

对数周期天线在没有进行橡胶阻尼减振优化时模型如图1所示，针对该天线在ANSYS中建立有限元模型，其涉及到的材料力学参数如表1所示，并按照图2所示振动图谱添加激励边界条件，进行5～2000 Hz的谐响应分析。

表1 结构材料力学性能参数

对数周期天线在ANSYS中Z轴激励谐响应分析下，在激励频率范围内的最大应力结果如图4所示，天线的馈电电缆内导体、天线的振子片及电缆外壳所受应力大幅超过了对应材料的屈服强度，印证了图2所示断裂故障的产生。其余轴向的谐响应分析在后续对比分析中给出对应结果，这里不再赘述。

图4 对数周期天线Z轴谐响应分析结果（Pa）

3.2 对数周期天线橡胶阻尼减振分析

为对数周期天线设计橡胶阻尼减振件，并采用原位替换的方式，添加到对数周期天线结构中，如图5所示，4个橡胶减振器通过减振过渡板转接到转接架上。橡胶减振器的材料参数如表1所示，选用的橡胶材料的耗损因子为0.8，则在ANSYS材料参数中设置Constant Damping Coefficient参数值为0.4。

图5 某对数周期天线添加橡胶阻尼减振优化构件

对数周期天线通过橡胶阻尼减振优化后，按照图2所示振动图谱进行谐响应分析，Z轴激励时，在激励频率范围内的最大应力分析结果如图6所示。从图6中可以看出，经过橡胶阻尼减振优化后，应力降低到了屈服强度以内，天线不会发生断裂。

图6 对数周期天线橡胶阻尼减振后Z轴分析结果（Pa）

3.3 对比分析

在ANSYS中对数周期天线3个轴向按照如图2所示图谱添加边界条件，进行谐响应分析，对比橡胶阻尼减振优化前与优化后的最大应力数据结果如图7所示，对比结果表明，进行橡胶阻尼减振优化后，天线的最大应力减小约50%，所有故障点附近应力均降到了材料许用应力范围内。如图8所示，在Z轴激励情况下馈电电缆与馈电后壁连接处的应力在整个振动频率范围内幅值优化超过60%。综上所述，对某对数周期天线进行橡胶阻尼减振优化有效。

图7 优化前与优化后故障点应力最大响应幅值

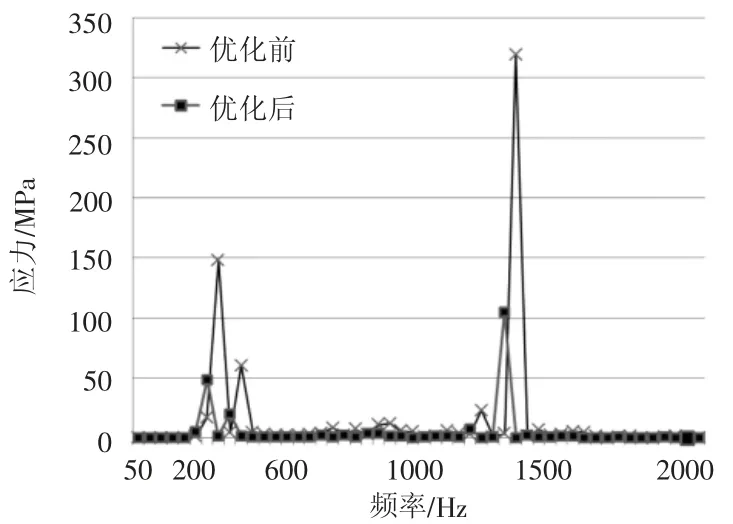
图8 Z轴激励优化前与优化后馈电点应力响应

4 试验验证

为复现在没有进行橡胶阻尼减振优化前的对数周期天线故障情况，对原天线进行了多次振动实验（如图9左），多个实物的振动实验表明，天线断裂不是个案，断裂故障点反复出现在图3所示的位置。

图9 天线的振动验证试验

为进一步验证进行橡胶阻尼减振优化后的对数周期天线能否满足振动耐久试验条件要求，对优化后的天线实物（如图9右）按照图2所示图谱分别进行X、Y、Z三个方向的振动试验，实验结果表明，天线结构完好，满足了环境试验条件要求，最终验证了对该天线的橡胶阻尼减振优化合理可行。

5 结语

为解决某对数周期天线结构的振动安全性问题，本文采用仿真和试验手段对其进行了研究。本文首先介绍了某对数周期天线的振动故障情况，列出了故障点发生位置，并补充了振动实验参数；然后论述了振动故障问题中涉及到的一些振动基本原理、振动图谱的计算、正弦扫频分析在ANSYS中表示方法和注意事项；随后对原天线进行了有限元仿真，复现了故障问题的发生；进一步对橡胶阻尼减振优化后的天线进行了有限元分析，并通过对比分析优化前后的结果，在数值仿真下验证了减振优化的可行性；最后，利用未优化的实物振动实验复现了故障点，并对橡胶阻尼减振优化后的天线完成三个轴向的耐久振动验证工作，最终验证了橡胶阻尼减振优化合理可行。

本文对阻尼减振进行了基本认识，说明了阻尼在ANSYS动力学计算中的表示方法，特别说明了阻尼在ANSYS以模态为基础的动力学分析中的计算原理，并形成对工程师的建议：在处理材料阻尼等问题时推荐采用完全法进行求解。本文能帮助工程师对工程样机如何做谐响应分析有一个基本的流程认识：从振动图谱的基本计算和认识，到ANSYS软件的边界条件和基本参数的确定，最后到分析结果与实验结果的印证。因此本文对工程师完善阻尼减振的认识、振动仿真计算和工程实践具有一定的参考价值。

本文对橡胶阻尼减振优化分析及应用问题上的研究偏工程领域较多，理论体系还不甚严密，还有一些问题有待进一步研究：1）在ANSYS中有更为专业的阻尼单元可以用来模拟阻尼特性，并能严格地描述阻尼的频率或温度变化特性；2）橡胶的阻尼参数还需要实验校核和验证；3）为更好地研究阻尼对响应的减幅作用，可将双振幅图谱转化为时域激励边界，对系统进行瞬态动力学分析，使得结果更为详细、直观和准确等。