广义整体最小二乘粗差探测的三维坐标转换方法

申仲舒,项谦和,董思学,韦天赦

(1.浙江省测绘科学技术研究院,浙江 杭州 311122; 2.中国地质大学(武汉),湖北 武汉 430074;3. 中国煤炭地质总局浙江煤炭地质局,浙江 杭州 310021)

在大地测量、摄影测量和计算机视觉等领域,三维坐标变换是将观测数据从原始坐标系转换至目标系统的常用方法。三维坐标转换最重要的步骤是确定7个转换参数(1个尺度比参数、3个平移参数和3个旋转角参数)。当旋转角足够小且尺度比接近1时,三维坐标转换数学模型可以简化为著名的布尔莎模型,通常用线性Gauss-Markov(GM)模型来描述。然而,实际中旋转参数和尺度参数可能是任意的,因此,一些研究采用最小二乘法求解非线性系统[1-2]。

由于实际中原始坐标通常也是观测所得,矩阵系数中的某些元素不可避免地会受随机误差的影响。因此,转换模型不能用GM模型描述,此时应引入变量误差(EIV)模型[3]。EIV模型的参数估计方法首先由文献[4]在数值分析领域提出,并命名为TLS,此后,又提出了许多算法,尤其是WTLS算法[5-6]。从应用的角度看,TLS的研究已经被引用到许多实际的问题中,如直线拟合、坐标转换、GNSS单点定位、遥感影像配准。近年来,TLS方法被用来解决三维坐标转换问题(任意旋转参数和尺度参数)已经成了研究热点[2,7]。

上述的TLS算法只有在原始坐标和目标坐标中仅包含偶然误差时适用。然而,如果观测值受到粗差污染,用这些方法获取的转换参数也会受到不利影响甚至严重失真。目前,对于TLS解法的粗差处理问题也有一些研究[1]。然而,由于标准EIV模型形式上的限制,所有的这些方法在大旋转角和任意尺度比的三维坐标转换问题中不适用[8-10]。

本文将三维坐标转换数学模型抽象为非线性EIV模型,并对Amiri-Simkooei and Jazaeri[11]的思路进行推广,将数据探测法拓展至该模型中。首先,利用Euler-Lagrange方法推导出非线性EIV模型的GTLS解。然后,将其等价转化为经典最小二乘问题,分别在方差分量已知和未知方差的条件下,基于经典最小二乘理论,构造两类数据探测的检验统计量。最后,采用试验数据对三维基准转换新算法的粗差探测性能进行验证[7]。

1 非线性EIV模型的WTLS和数据探测算法

1.1 非线性EIV模型的GTLS解法

三维坐标转换数学模型公式为

(1)

转换公式可写为非线性EIV模型的形式

L-eL=f(a-e1,ξ)=φ(e1,ξ)

(2)

式中,f和φ都是n×1维的抽象向量函数;a和L分别代表在原始和目标系统中m×1维和n×1维的观测向量;e1和eL分别为a和L的随机误差向量;ξ为一个j×1维的未知参数向量。

相应的随机模型为

(3)

其中

(4)

式中,Q为粗差向量e的正定协因数阵;QLL和Qaa分别为eL和e1的协因数阵;QLa和QaL为eL和e1之间的相关协因数阵;σ02为方差分量。上述模型的估计准则为

eTQ-1e=min

(5)

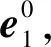
(6)

其中

(7)

A和B需要在迭代过程中不断更新。以此构造拉格朗日目标函数为

(8)

式中,λ为拉格朗日乘子的n×1维向量。利用Euler-Lagrange必要条件可解出

(9)

(10)

(11)

式中,“～”和“＾ ”分别表示预测值和评估值。

从式(9)可以得到误差向量

(12)

(13)

(14)

将式(12)代入式(11)

(15)

其中

QT=GQGT=QLL+QLaBT+BQaL+BQaaBT

(16)

将式(15)代入式(10),可以获得δξ的表达式

(17)

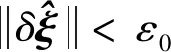
1.2 GTLS算法重构

式(6)可以写成如下形式

l=Aδξ+el

(18)

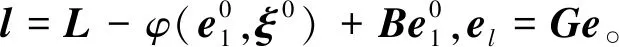
将Ql作为l的协因数阵,两边对式(18)取方差

(19)

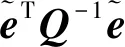
(20)

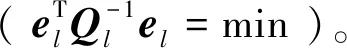
(21)

基于上述证明,非线性EIV模型可以利用经典最小二乘理论知识。误差向量el估计为

(22)

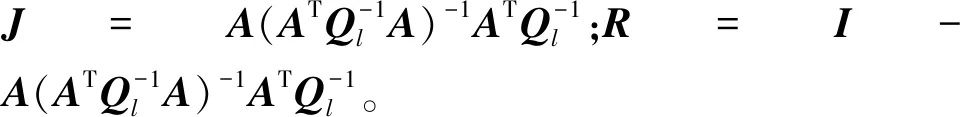
因此式(13)、式(14)可写成如下形式

(23)

(24)

此外,估计参数的后验方差因子和协方差矩阵可估计为

(25)

(26)

由于非线性EIV模型的GTLS估计是一个非线性问题,其参数估计及其精度评估是有偏差的。尽管在实践中偏差可能很小,为了获得偏差的影响,可以参考文献[5]提供的方法,此方法已应用于标准EIV模型和约束TLS问题。

1.3 数据探测算法应用于非线性EIV模型

如果观测数据受粗差污染,参数估值将不可靠。可在方差分量已知和未知的情况下,分别采用正态检验和t检验来检测和消除粗差[12]。当方差分量已知时,第i个观测方程的检测统计量为

(27)

当方差分量未知时,第i个观测方程的检测统计量为

(28)

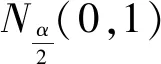
基于局部敏感性分析,可将这两种检验统计量推导出来。在相关观测数据的情况下,它们对检测粗差更为敏感[11]。

在出现多个粗差的情况下,应持续实施探测过程,这个过程叫作“数据探测”。当单位权方差分量已知时,如果

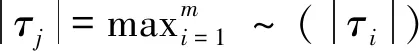
(29)

或单位权方差分量未知时,

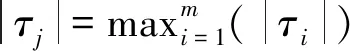
(30)

即消除观测方程。如果满足以上等式,则证明相应的观测方程中存在粗差。粗差可能在观测向量L或向量a中,甚至在两者中。应将标记的观测方程从方程表中删除,然后调整剩余的数据,重复执行此过程,直至所有统计检验都被接受。

2 数据探测算法在三维坐标转换中的应用

在三维坐标转换算法的应用中,需要确定矩阵A和B的具体表达式。

假设共有k个公共点,则相应维数分别为m=n=3k和t=7。

对于第i个公共点

(31)

(32)

其中

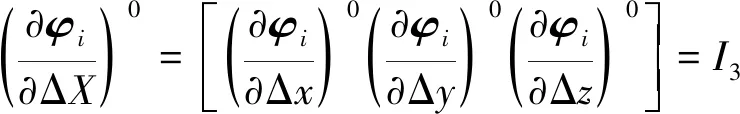
(33)

(34)

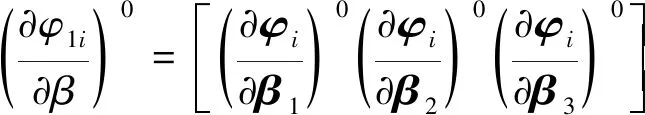
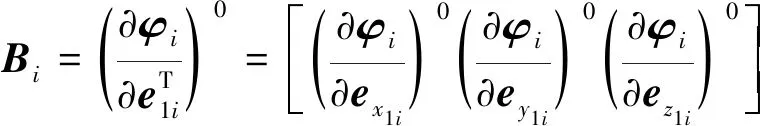
=-μ0·M0

(35)

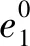
(36)

(37)

通过将每个点的相应表达式组合在一起,得到矩阵A和B为

(38)

3 试验分析

假设有36个点分布在一个空间域中。已知源坐标系(a系统)和目标坐标系(b系统)中每个点的实际坐标。从系统a转换到系统b的7个参数如下:Δx=1000, Δy=1000, Δz=1000,μ=1.5,β1=1.0 rad,β2=1.5 rad,β3=-0.5 rad。

本文将26个点作为公共点,其余10个点是检核点。根据已知的协方差矩阵,每次模拟均会产生相关随机误差。在含有随机误差的坐标中引入5个粗差,其大小介于(-30,-5)和(5,30)倍的先验标准差之间,位置随机产生,反复进行500次模拟。

设计以下3种计算方案来求解转换参数:①在引入粗差之前,对非线性EIV模型进行了GTLS估计,并在引入粗差之后进行了以下两种方案;②非线性EIV模型的GTLS解法;③非线性EIV模型的数据探测算法,由于方差分量已知,本方案中采用正态分布检验(α=0.05)。

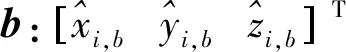
(39)

总中误差为

(40)

上述方案的统计结果见表1,包含σx、σy、σz和σp的平均值和最大值,此外,图1为方案2和方案3的试验对比结果。

表1 不同转换方案中误差统计 m

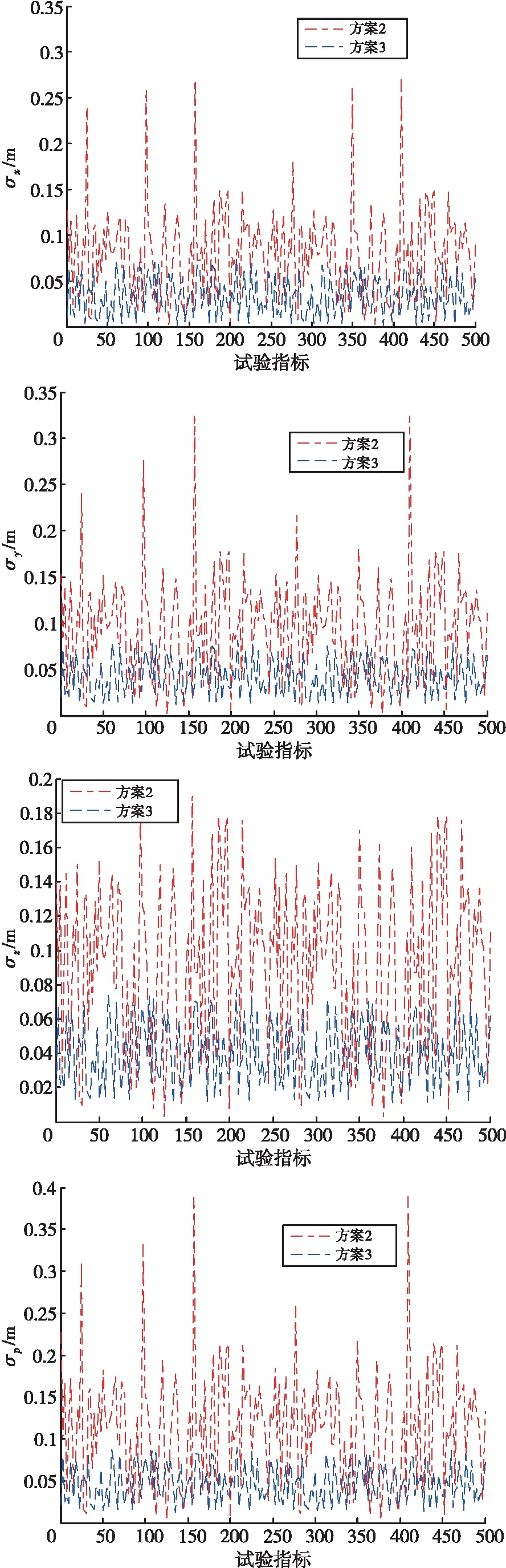
图1 转换方案2和3的试验结果对比

(1)当粗差引入前,GTLS估计(方案1)得到了3种方案之间的最优转换参数。

(2)引入粗差后,GTLS(方案2)得到的转换参数严重失真,因此,在模拟过程中,方案2中存在许多大的均方根误差,此外,σx、σy、σz和σp的对应平均值均增加了约3倍。

(3)与GTLS算法相比,非线性EIV模型的数据探测方法(方案3)能有效地提高转换坐标的精度。所有方向的最大中误差明显小于方案2的最大中误差。还可看出,方案3的σx、σy、σz和σp的对应平均值分别仅为方案2的39.4%、36.9%、41.6%和38.4%。尽管方案3的结果不如方案1,但它们之间的差异并不显著。因此,非线性EIV模型的数据探测方法得到的转换参数仍然是十分可靠的[13-14]。

4 结 语

为了处理严密三维坐标转换的粗差处理问题,本文将数据探测算法应用于非线性EIV模型中。首先用Euler-Lagrange方法推导出了非线性EIV模型的GTLS迭代解,然后用经典最小二乘法对其进行了重构。分别在已知和未知方差分量因子的条件下,基于经典最小二乘理论,构造了数据探测的两个检验统计量。这里需要指出该算法可以看作是Amiri Simkooei和Jazaeri算法的一种推广形式[8,11,15]。

试验及其结果表明,该算法能有效削弱粗差的影响,获得可靠的转换参数。与WTLS估计相比,所得参数的精度和准确度有了显著提高。