谈凹凸反转法在解题中的妙用
刘海涛
(安徽省芜湖市第一中学,安徽 芜湖 241000)
在处理一些不等式(或等式)问题时,若我们直接研究函数解析式,将问题转化为函数最值问题处理,则往往由于函数式比较复杂,需要讨论参数、运用隐零点求最值等,使解答过程繁杂,运算量大,但若能将不等式(或等式)合理变形为m(x)≥n(x)(或m(x)=n(x)),其中m(x)为凹函数,n(x)为凸函数,且m(x)min≥n(x)max(函数m(x)的最小值点与函数n(x)的最大值点相同),则可以通过分别研究函数m(x)与n(x)的单调性,来完成对问题的解答.一般地,我们把这种将不等式(或等式)“一分为二,分而治之”的解题方法,称为“凹凸反转法”.
1 例谈凹凸反转法的应用
1.1 证明不等式问题中的应用
例1已知函数f(x)=2ex-2+ax(a>0),对∀x>0,求证:f(x)>x(lnx+a).
解法1由f(x)>x(lnx+a),得2ex-2>xlnx.
设g(x)=2ex-2-xlnx,下证g(x)>0即可.
求导,得g′(x)=2ex-2-lnx-1,
易知g″(x)在(0,+∞)上单调递增.
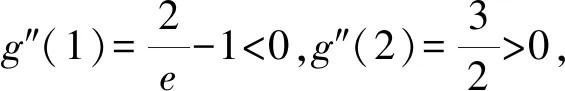


又x→0时,g′(x)→+∞,g′(2)=1-ln2>0,则存在x1∈(0,x0),x2∈(x0,2)使得g′(x1)=g′(x2)=0.
于是当0 因此欲证g(x)>0, 即证g(x2)>0,即证2ex2-2-x2lnx2>0. 又由g′(x2)=0,得2ex2-2=lnx2+1. 即证lnx2-x2lnx2+1>0. 设h(x)=lnx-xlnx+1(1 又h(2)=1-ln2>0,所以h(x2)>0. 故问题得证. 解法2由f(x)>x(lnx+a),得 2ex-2>xlnx. 所以m(x)min>n(x)max. 评注解法1直接作差构造函数,将问题转化为求函数最小值大于0,解题过程中两次运用隐零点法,过程繁杂,运算量大;解法2将不等式合理变形,分离为凹凸反转的两个函数,分别研究两函数单调性,将问题转化为左侧函数最小值大于右侧函数最大值问题.比较解法1和2,不难发现凹凸反转法的优势,大大简化了解题过程[1]. 解法1由不等式f(x)≤g(x),得 ex+x2-lnx-ax≥0. 当x→0+时h′(x)→-∞,当x→+∞时h′(x)→+∞,则存在唯一x0∈(0,+∞)使h′(x0)=0,于是当0 两式联立消去a,整理得 (1-x0)(ex0+x0+1)-lnx0≥0. 设φ(x)=(1-x)(ex+x+1)-lnx, 有φ(x0)≥0, 函数φ(x)在(0,+∞)上单调递减,注意到φ(1)=0,得0 故a≤y(1)=e+1. 解法2不等式f(x)≤g(x)整理为 当0 由此问题转化为m(1)≥n(1),得a≤e+1. 评注解法1直接作差构造函数,将问题转化为h(x)min≥0,运用隐零点法求出函数的最小值;解法2将不等式变形为m(x)≥n(x),分别研究两函数发现x=1恰是函数m(x)的最小值点,n(x)的最大值点,符合凹凸反转的特点,于是不等式等价于m(1)≥n(1). 解法1由f(x)≥lna+2,得 易知g′(x)在(0,+∞)上单调递增. 设x1 g′(x1)<0,g′(x2)>0. 所以存在x0∈(x1,x2)使g′(x0)=0,当0 即lna=x0+lnx0-2. 易知φ(x)在(0,+∞)上单调递减. 又φ(1)=0,则0 所以lna=x0+lnx0-2≤-1. 解法2由f(x)≥lna+2,整理,得 所以m(x)min=m(1)=e. 1.3含参不等式有若干整数解问题中的应用 所以m(x)min=m(e)=a-e2. 评注受例4的启发,将方程转化为等号两侧凹凸性相反的两个函数,问题转化为m(x)min=n(x)max. 通过上述例题的解答,不难发现,若不等式(或等式)中含有ex,lnx时,我们可以考虑用凹凸反转法处理不等式(或等式),这为我们今后处理不等式(或等式)提供了一种新的思路,但该种解法并非通法,有局限性,只有在符合特定的情形下方可使用.另外,熟记一些与ex,lnx有关的函数,往往有利于我们探究问题时使用凹凸反转法,笔者通过梳理,给出以下函数的草图供读者使用(如图1). 图1 与ex,lnx有关的函数图

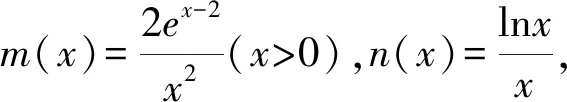
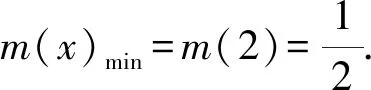
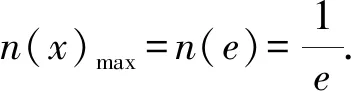

1.2 含参不等式恒成立求参数问题中的应用
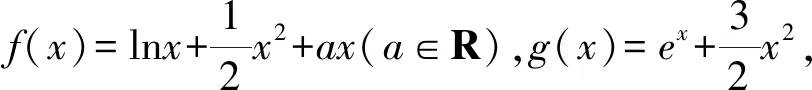
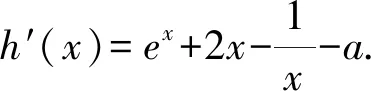
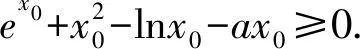
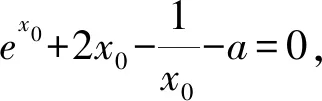


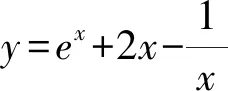
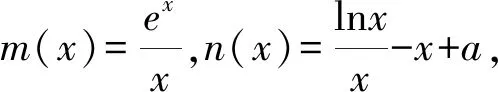
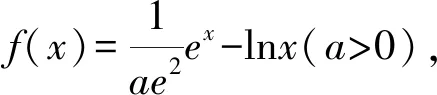
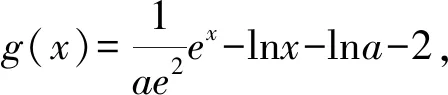
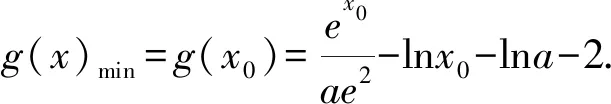
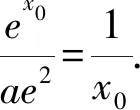
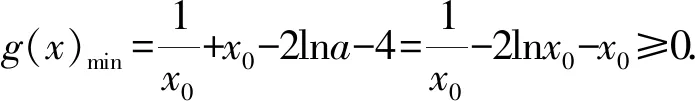

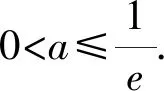
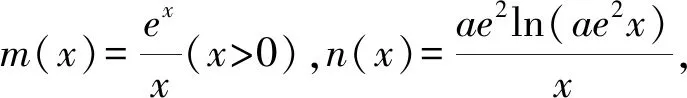
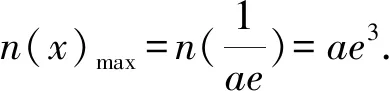
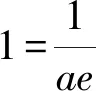
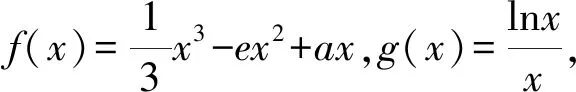
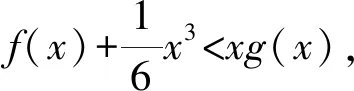
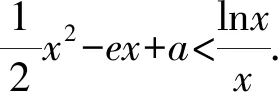
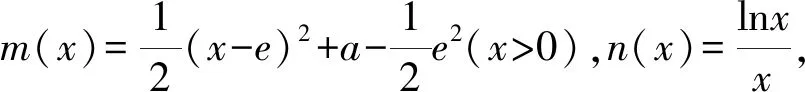
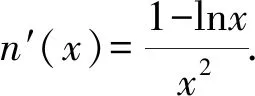
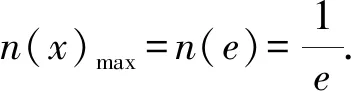
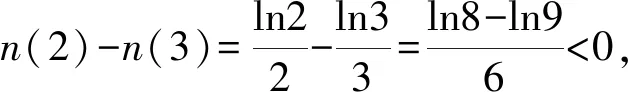
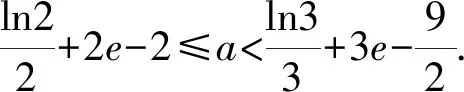
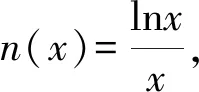
1.4 方程有解问题中的应用

2 反思小结


