CEEMDAN 与参数优化多尺度排列熵结合的滚动轴承早期故障诊断

谢锋云，刘慧，胡旺，赏鉴栋，姜永奇

（华东交通大学 机电与车辆工程学院 ，南昌 330013）

滚动轴承作为关键的机械零部件，在各大旋转机械设备以及高铁、飞机等现代化交通工具中得到了广泛应用，它的健康状况对于设备的安全可靠运行有着重要的影响。

Torres 等[1]提出自适应噪声完备集合经验模态分解（Complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN），它是对集合经验模态分解（Ensemble empirical mode decomposition,EEMD）算法的一种改进，通过在信号分解的每一阶段添加自适应噪声，有效的解决了模态混叠等问题并拥有较小的重构误差[2]，因而广泛应用到故障诊断的降噪处理中。杨保俊等[3]应用CEEMDAN 与峭度-相关系数对信号重构，并用复合神经网络对故障进行了有效识别；蒋玲莉等[4]提出了以CEEMDAN排列熵为敏感特征量，支持向量机进行模式识别的螺旋锥齿轮故障诊断方法。

近年来，熵值作为一种能够反映信号的复杂程度以及随机性的指标，被广泛作为故障诊断领域的特征向量。徐乐等[5]利用局部均值分解（LMD）的能量熵和支持向量机（SVM）相结合，对滚动轴承的故障类型进行识别和分类；郑近德等[6]用局部特征尺度分解（LCD）和排列熵对滚动轴承进行故障诊断。多尺度排列熵（Multi-scale permutation entropy, MPE）是Aziz 等[7]在排列熵的基础上进行多尺度粗粒化的改进的提取故障特征的方法，它可以反映信号在不同尺度下的复杂性与随机性。郑近德等[8]用MPE和SVM 有效的提取出了滚动轴承的故障特征。故障状态不同时，信号的复杂程度也不同，相较于文献[8]的MPE 的参数选取固定，在其基础上，运用粒子群优化算法[9]（Particle swarm optimization, PSO）对其参数进行优化，以达到不同故障时MPE 参数也不同，提高识别率的效果。

SVM 是一种建立在统计学习理论基础上的机器学习方法[10]，最初是专门针对小样本情况提出的分类方法[5]，所以SVM 在训练样本很少时，也能得到很好的分类效果，因此在故障诊断领域得到了广泛应用，尤其是小样本情况下的故障诊断场合。

由于滚动轴承早期故障振动信号是非平稳、非线性的，且在多个尺度上包含故障信息，因此提出一种基于CEEMDAN、PSO-MPE 相结合的滚动轴承早期故障特征提取方法，运用SVM 实现故障的模式识别。与CEEMDAN-MPE-SVM、MPE-SVM 的识别结果进行了比较，验证该方法的有效性和优越性。

1 基本理论

1.1 CEEMDAN 基本原理

与EEMD 分解过程中每次加入高斯白噪声EMD分解后再对得到的固有模态函数（Intrinsic mode function, IMF）取平均不同，CEEMDAN 在信号每次分解后的残差中添加特定的标准正态高斯白噪声后EMD 分解，并计算唯一的残差获得每个IMF[1]，实现了自适应加噪，且信号的重构误差几乎为零[4]。因此，CEEMDAN 不仅提高了分解精度，也避免了经验模态分解（Empirical mode decomposition,EMD）分解会带来的模态混叠问题，减少了虚假IMF 的产生[4]。

CEEMDAN 的分解步骤如下：

x(n)+e0wi(n)

1）对原始信号x（n）加噪得到： ，对其进行I次EMD 分解，取其平均值得到

1.2 MPE 基本原理及参数选择

1.2.1 MPE 基本原理

多尺度排列熵即多个尺度下的排列熵，和排列熵一样，也能反映信号复杂性与随机性。多尺度排列熵的计算方式为：将长度为N的时间序列X={x1，x2，x3， ···，xN}，经过粗粒化后，求其排列熵[8]。具体的计算步骤如下：

1）对时间序列X= {x1，x2，x3， ···，xN}粗粒化处理，得到

式中：j=1，2，···，[N/s]，[N/s]为N/s向下取整，s为尺度因子。

2）对粗粒化后得到的序列重构，即

式中：m为嵌入维数； λ为延迟时间；l为重构分量，l=1，2，···，N-（m-1） λ。

3）将式（9）升序排列，每一个粗粒化序列都能得到一组新的序列s（v）=（lI，l2， ···，lm)，v=1，2，···，V，V≤m!，s（v）的数目与重构序列m!的数目一致。

4）计算不同尺度下的排列熵

式中Pv为第v次符号序列出现的概率。

式中：HP越小，该时间序列越有序，越有可能处于故障状态，HP越大，该时间序列的规律性越弱，处于正常状态的可能性越大。

1.2.2 MPE 参数选择

计算信号的MPE 值时，嵌入维数m和尺度因子s的值对计算结果影响较大。当m太小，重构序列中包含的状态过少，对信号的突变性检测降低，算法有效性降低；当m太大，计算量加大且对于时间序列的细微变化反应不明显[9,12-13]。当s过小，信号所包含的特征信息不能被有效的提取；当s过大，信号之间的复杂的关系可能会被忽略[9,12]。延迟时间t及数据长度N对时间序列的分析结果也有一定的影响。为取得更好的识别效果，应用粒子群优化算法对以上4 个参数进行寻优操作。

1.3 SVM 基本原理

SVM 的目标是在输入特征空间上找到一个最优超平面对原样本尽可能多的进行正确分割，且使每类样本到该平面的距离最大，即构造一个约束二次规划问题，求解该问题，得到分类器[14]。SVM 通过核函数可将待分类的非线性低维数据映射到高维特征空间，然后在特征空间中借助最优超平面构造判决函数找到线性关系来解决非线性问题，在很大程度上克服了小样本、维数灾难及非线性等问题[10]。

2 故障识别流程

滚动轴承早期故障诊断方法流程图如图1 所示。

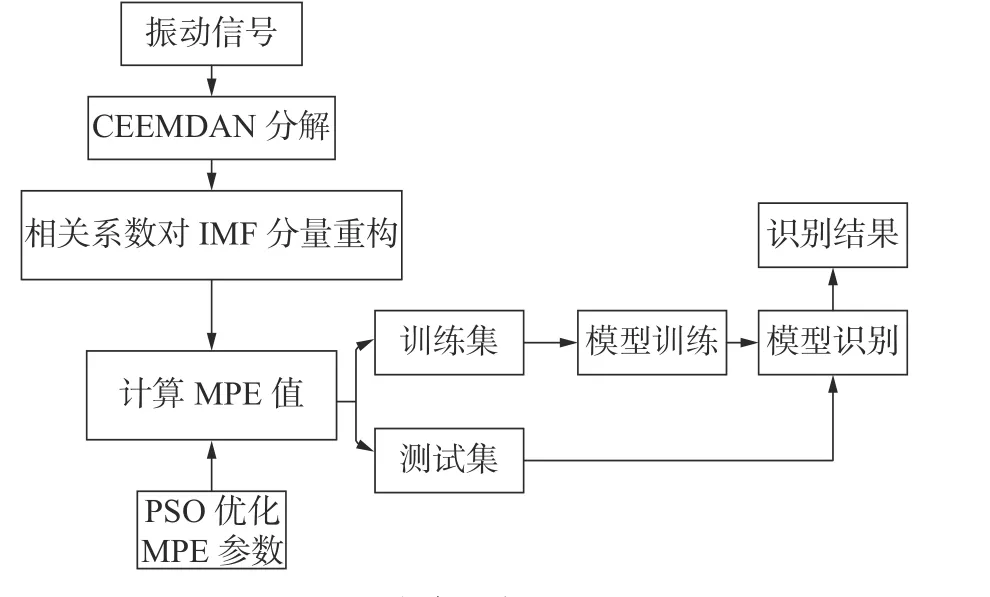
图1 故障诊断流程图Fig.1 Fault diagnosis process flowchart

故障诊断的步骤如下：

1）设定CEEMDAN 的参数，对滚动轴承的4 种状态信号进行分解，得到对应的IMF 分量。

2）计算各IMF 分量与原始信号的相关系数，并由相关系数阈值公式得到各组数据的相关系数阈值，将小于相关系数阈值的分量删去，对大于相关系数阈值的IMF 分量进行重构。

3）对MPE 参数的搜索范围进行设定，利用PSO 算法对MPE 从设定的初始值进行遍历寻优，得到优化后的MPE 参数。

4）利用优化后的MPE 参数计算经CEEMDAN分解重构后的信号的MPE 值，组成故障特征向量。

5）将故障特征向量分为两部分：每种状态中30 组作为训练集，70 组作为测试集，将训练样本输入SVM 进行模型训练，得到训练好的SVM 分类模型。

6）将测试样本输入上述训练好的模型中进行状态识别，得到测试集的滚动轴承状态结果。

3 滚动轴承故障诊断实例分析

采用西安交通大学的滚动轴承加速寿命试验数据来进行验证。该实验的对象为LDK UER204 滚动轴承，轴承的振动信号采用DT9837 便携式动态信号采集。采样频率25.6 kHz，采样间隔为1 min，每次采样1.28 s；轴承的转速为2 250 r/min，所受径向力为11 kN，试验平台[15-16]如图2 所示。

图2 XJTU-SY 滚动轴承加速寿命试验平台Fig.2 XJTU-SY rolling bearing accelerated life test platform

测试轴承的详细信息如表1 所示。再将CEEMDAN 分解重构后的信号直接计算MPE 值，同时直接计算原始信号的MPE，分别组成故障特征向量，同样运用SVM 进行模式识别，将识别结果与本文所提方法进行对比分析。

实验截取Bearing2_1 故障发生前的部分数据作为滚动轴承的正常状态的数据，并选取Bearing2_1、Bearing2_2、Bearing2_3 故障刚发生时的数据作为故障数据，取滚动轴承4 种运行状态的信号各100 组数据，30 组训练集，70 组测试集，进行故障状态的特征提取与模式识别。

本文随机选取保持架故障的一组数据进行处理。对其进行CEEMDAN 分解（加入白噪声标准差为0.2，噪声添加次数为100 次）得到的结果如图3 所示。

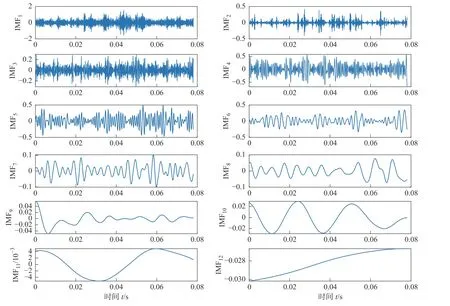
图3 CEEMDAN 分解效果图Fig.3 CEEMDAN decomposition effects

相关系数是能够体现两组信号相关性大小的参量，相关系数越大，则两组信号越相似，反之亦然。根据皮尔逊相关系数计算各IMF 分量与原始信号的相关系，即

各IMF 分量与原信号相关系数如表2 所示。

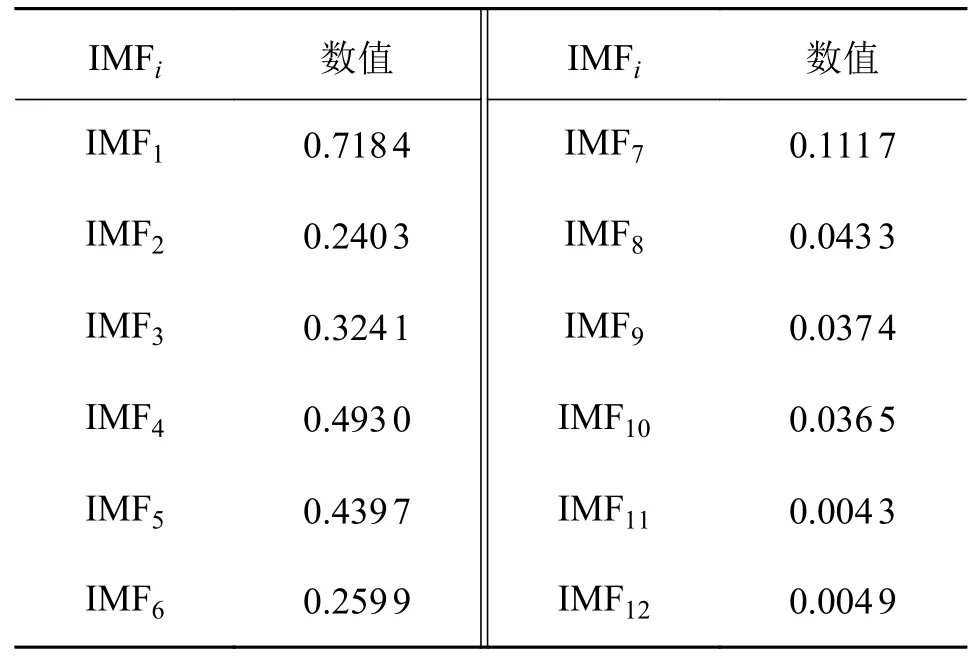
表2 各IMF 分量与原信号相关系数Tab.2 Correlation coefficients between each IMF component and original signal

滚动轴承不同状态下的相关系数的阈值计算式为

得到上述保持架故障的相关系数阈值为0.171 6，将相关系数大于0.171 6 的对应IMF 分量（IMF1～ IMF6）进行重构，相关系数小于0.171 6 的IMF 分量去除。

对滚动轴承4 种状态下的每种状态100 组数据分别做上述预处理，得到各状态下的重构信号。

PSO 算法参数[9]如下：种群规模为10，最大迭代次数为20，加速常数为1.5，惯性权重为5，设置MPE 参数寻优范围为：m∈3 ～ 7，s∈1 ～ 16，t∈1 ～ 5，N∈128 ～ 2 000。对PSO 算法运行10 次求其平均值[9]，向下取整得到各状态下信号的多尺度排列熵算法的优化参数，结果如表3 所示。

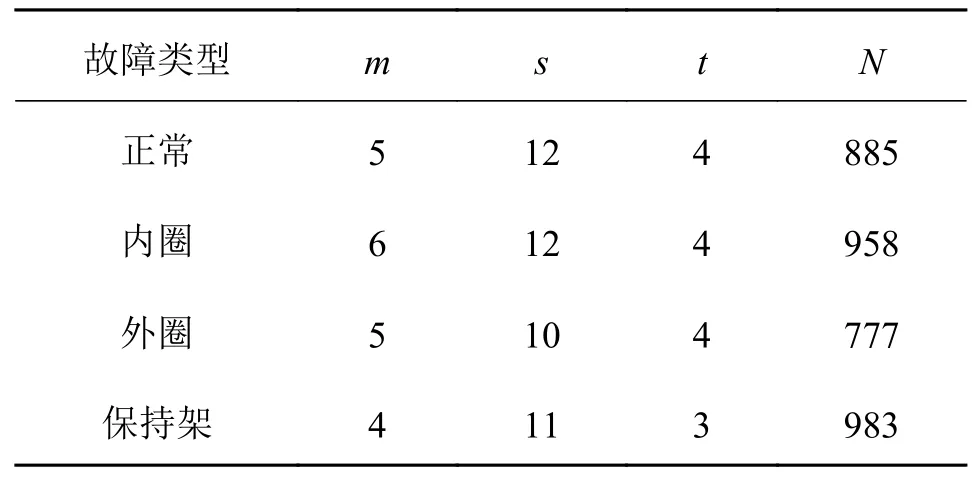
表3 PSO 寻优的MPE 参数Tab.3 MPE parameters optimized by PSO

运用表3 的参数计算滚动轴承的4 种状态的MPE 值，每种状态尺度因子的值按照表中最小的值进行取值，其中一组的结果如图4 所示。

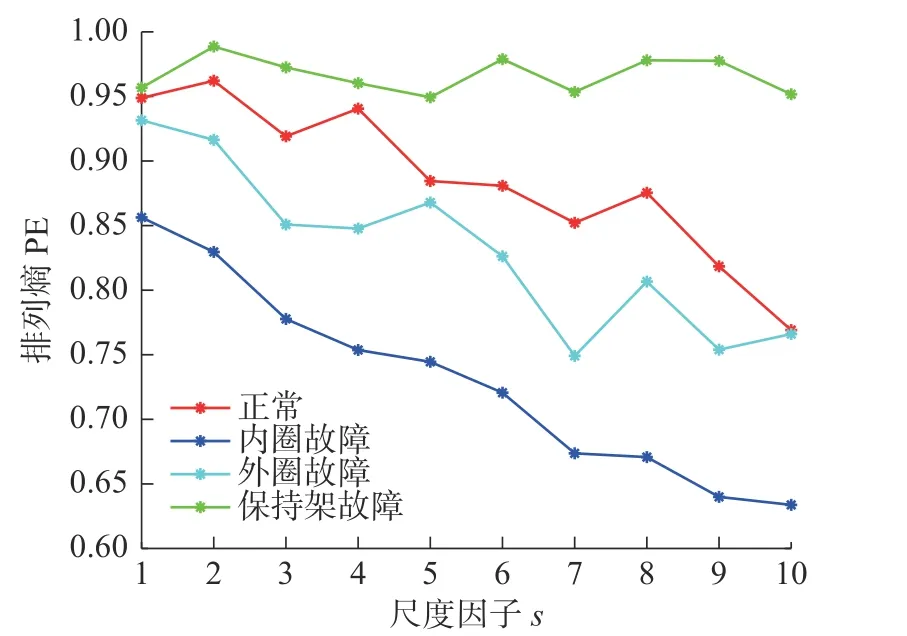
图4 轴承4 种状态参数优化后MPE 值Fig.4 MPE values after optimizing parameters for 4 states of a bearing

从图4 可以看出，经过参数优化后的滚动轴承4 种状态的MPE 值差异明显，能够比较清晰的分辨出4 种状态。按参考文献[8]选定的的参数，取m=6，s= 12，t= 1，计算重构后滚动轴承4 种状态下的MPE 如图5 所示。

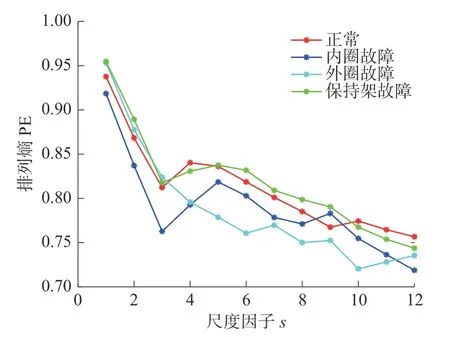
图5 参照文献设定的参数的MPE 值Fig.5 MPE values of parameters set according to reference literature

从图5 可以看出，参照文献设定的MPE 的参数得到的4 种状态下滚动轴承的MPE 值存在一定的交叉现象，不能够很好的区分出不同的故障状态。

将得到的两组故障特征向量分别应用SVM 进行状态识别，得到的结果如图6a）、图6b）所示，将未经过CEEMDAN 分解重构也未对MPE 的参数进行优化计算得到的MPE 值也进行SVM 模式识别，识别结果如图6c）所示。滚动轴承4 种状态的具体识别结果如表4 所示。

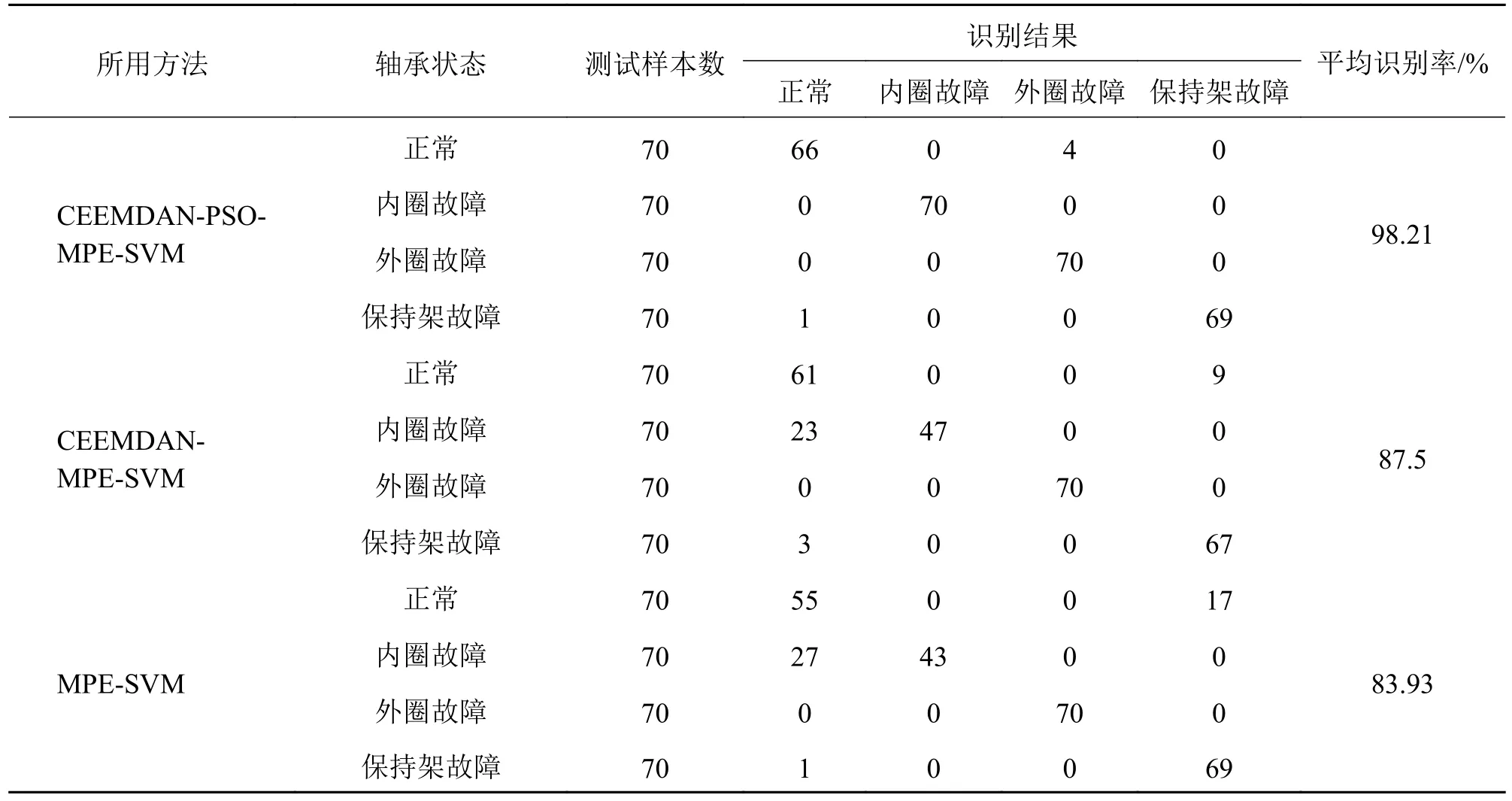
表4 故障诊断结果Tab.4 Fault diagnosis results

图6 识别结果比较Fig.6 Comparison of identification results

由表4 可知，当使用参考文献设定的MPE 参数，且不对信号进行CEEMDAN 分解重构时，有45 组样本被识别错误，SVM 的识别率约为83.93%，对比将信号进行CEEMDAN 处理后的识别结果（35 组被识别错误，总体识别率为87.5%），此时识别率提高了3.57%，而使用本文所提方法即对MPE 的参数优化后计算CEEMDAN 分解重构后的信号的MPE 值作为故障特征向量运用SVM 进行故障状态识别时，识别错误的组数为5 组，总体识别率为98.21%，相比于MPE 的参数未优化时，识别率提高了10.71%。说明：在利用CEEMDAN 对信号进行分解重构时，剔除掉了部分与原始信号相关性小的分量，使重构后的信号的故障特征较未处理前更明显，故而识别率得到了提高；使用优化后的参数求取信号的MPE 值时，考虑了MPE 参数对于分解结果的影响，每种状态的参数都不相同，所以识别结果得到了大幅提高。以上结果验证了本文所提方法对于滚动轴承早期故障诊断的有效性。

4 结论

1）对原信号进行CEEMDAN 分解，运用相关系数阈值对分量进行重构，剔去了与原信号相关性不大的噪声分量。

2）考虑到不同信号的复杂程度不同，对MPE的参数进行PSO 寻优，得到了各种状态信号的MPE 参数。

3）将本文所提方法得到的各状态的MPE 值组成故障特征向量，与MPE 参数未优化以及未CEEMDAN 分解且MPE 参数未优化得到的MPE值作为特征向量，使用SVM 的识别结果进行对比，本文所提方法识别率得到了大幅提高。