重型机械臂电液系统的神经网络辨识与反步控制

刘汇，王恒升，郭新平，孙晓宇

（中南大学 机电工程学院，长沙 410083）

电液驱动因其响应速度快、结构简单、功率密度大等优点被广泛应用于重型工程机械设备[1]上，其防爆优势对隧道、矿山的工程应用更为突出。随着对矿山建设自动化要求的提高[2]，电控液压驱动系统大量应用在这类工程装备上。电液驱动系统的运动控制是具有基础性和共性的问题，是进一步实现自动化、智能化必须要解决的问题。本文以某锚杆钻车重型机械臂的自动定位为应用背景，研究其机械臂电液系统的控制，其难点来源于系统的高度非线性、参数的时变与不确定性以及动态负载的时变性，这些因素对位置跟踪的快速性和精确性提出了更大的挑战。

传统上一般采用机理建模[3]的方法建立电液系统的模型，但机理建模无法获得准确的模型参数，对此一些研究人员采用离线参数辨识或在线参数自适应的方法解决这一问题。文献[4-5]使用递推最小二乘法在线辨识电液系统的非线性Hammerstein 模型，并设计了相应的自适应控制器。Yuan 等[6]使用灰箱模型估计电液伺服系统的微分方程模型，并采用模型预测控制算法提高了系统的静态和动态特性。余臻等[7]通过辨识获得电液伺服系统以误差为状态变量的多项式非线性模型，在此基础上设计了非线性鲁棒控制器。然而参数辨识和在线参数估计只能解决电液系统参数不确定的问题，难以保证系统在动态负载下仍具有良好的稳定性和瞬态性能[8]。

针对传统参数自适应无法解决高度非线性和动态负载问题，神经网络提供了一种有效地解决途径。RBF 神经网络[9]具有对任意非线性函数逼近的能力，可以在线估计系统的不确定因素[10]，在很多控制系统中都得到了应用。李砚浓等[11]基于RBF 神经网络设计自适应PID 控制方法以解决四旋翼飞行器的高度非线性问题。秦斌等[12]在滑模控制的基础上引入RBF 神经网络以改善风力发电系统的动态性能。赵希梅等[13]针对永磁同步电机存在的负载扰动等不确定性，将反步控制与RBF 神经网络相结合，提高了控制系统的跟踪性和抗扰性。RBF 神经网络控制对于非线性和时变特性强的电液系统也同样适用[14-20]，何玉彬等[21]将神经网络应用到大型电液系统的控制当中，利用神经网络在线学习电液系统的未知动力学。

采用何种控制方法能实现电液系统的高性能控制一直是液压控制领域的研究热点，反步法由于能有效补偿系统中的非匹配干扰，且设计过程简单，近年来受到电液系统控制器设计者的关注。刘胜斐等[22]在反步控制的基础上使用线性扩张状态观测器估计扰动，提高了比例阀控电液系统的精度与抗干扰能力。石胜利等[23]、Won 等[24]使用反步法设计电液系统的控制器，同时利用干扰观测器观测电液系统的不确定性干扰。

基于上述的分析，本文采用RBF 神经网络辨识和反步控制相结合的方法实现重型机械臂电液系统的位置跟踪控制。首先通过系统辨识实验获得机械臂电液系统模型中的标称参数，然后引入RBF 神经网络辨识动态负载。在此基础上，设计反步控制器，并根据控制误差和Lyapunov 理论对RBF 的中心、宽度和输出权值进行在线更新，同时分析了控制系统的稳定性。最后对机械臂的电液系统进行了仿真和实验研究，以锚杆钻车的大臂俯仰缸为例进行位置跟踪实验，验证了本文所设计控制算法的有效性。

1 机械臂电液系统模型

1.1 系统概况

锚杆钻车机械臂的结构如图1 所示，整个机械臂由大臂、小臂、推进器和凿岩机构成。机械臂整体由电液驱动，通过控制油缸带动各个关节运动，完成钻孔、装杆、紧固等一系列工序。本文针对锚杆钻车的大臂俯仰缸进行研究，通过俯仰缸控制机械臂进行升降。在升降过程中，俯仰缸所受到负载是动态变化的，若运动不连续则会引起机械臂发生抖动、卡顿的问题，因此该系统对控制系统具有较高的要求。

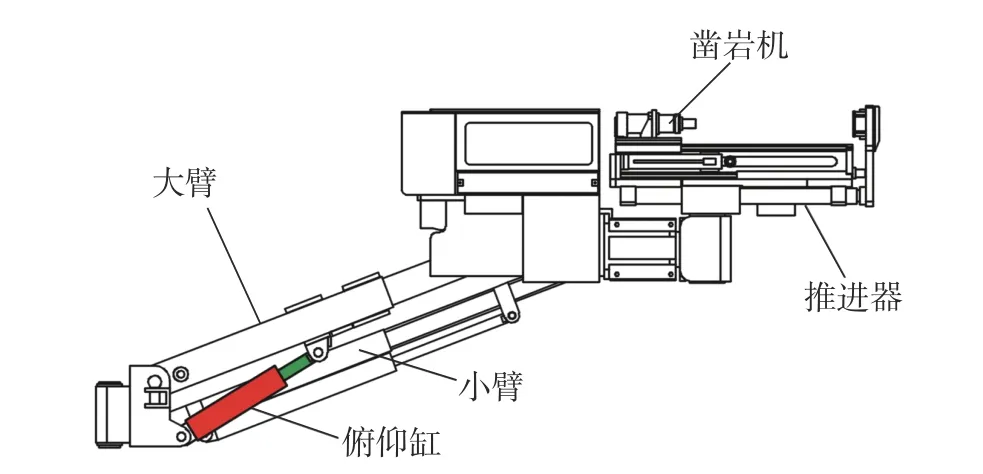
图1 锚杆钻车机械臂示意图Fig.1 Bolt drilling truck's manipulator structure

以机械臂的俯仰缸为例，其电液伺服系统如图2所示，主要由先导式比例换向阀、阀控非对称液压缸、油泵和油箱等构成。压力油进入电液比例方向阀，控制系统输出电信号调节比例阀开度以调节油液的流量，从而控制液压缸活塞杆的伸缩速度，通过液压缸活塞杆的运动推动机械臂关节运动。

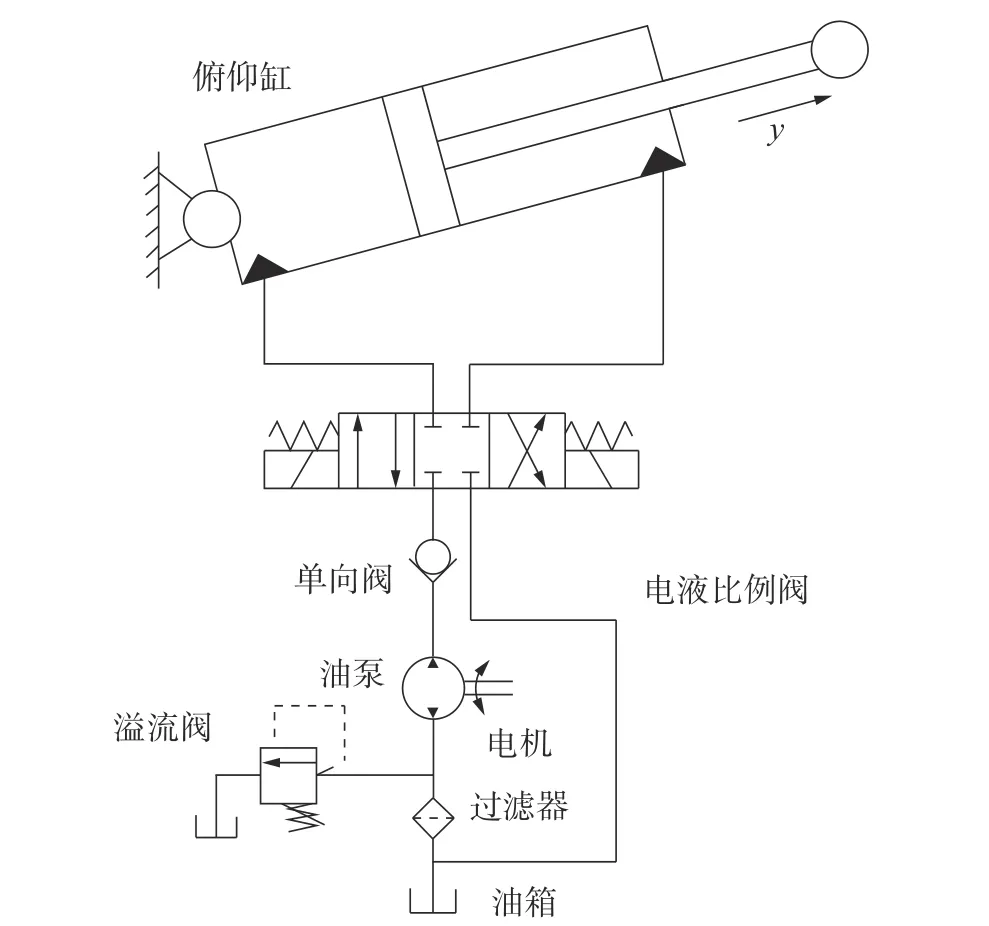
图2 机械臂电液系统示意图Fig.2 Manipulator's electrohydraulic system

1.2 电液系统等效模型

电液系统的数学模型由流量连续性方程、液压缸的力平衡方程和比例阀的输入流量关系构成。

电液系统的等效模型[25]可表达为：

式中：QL为负载流量；kq为比例增益；u为PWM 输入信号；At为液压缸的平均有效面积；y为液压缸位移；Cei、Ceo分别为液压缸的等效内、外泄露系数；PL为负载压力；Vt为等效总容积；βe为油液的有效体积弹性模量；m为活塞和负载的总质量；Bp为活塞黏性阻尼系数；Kp为负载弹簧刚度；Fs为液压缸运动阻力；FL为等效负载力。

根据式（1）构建电液系统的状态方程。选取液压缸活塞的位移、速度和加速度为状态变量，即[x1x2x3]T=[yy˙y¨]T，系统的输入为比例阀的PWM信号u，系统的微分阶次为3 阶，状态方程如下：

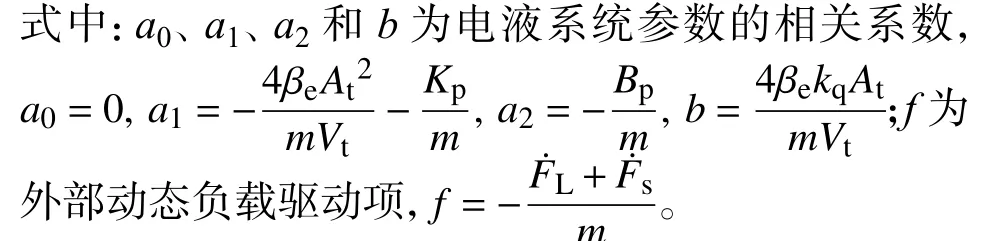
此处忽略了油液泄露系数，即Cei=Ceo=0。

令f0=a0x1+a1x2+a2x3，则从式（2）中可以看出驱动系统状态变化的3 个因素：内部的状态反馈项f0、控制器驱动项u和外部动态负载驱动项f。基于这一模型，本文的方法是将驱动放在加加速度（加速度的微分）的层次上，这对提高控制系统的动态性能大有好处。

针对系统内部状态反馈项，由于考虑电液系统的参数具有缓慢变化的特征，我们通过实验数据进行离线辨识这些参数，在实际控制过程中，这些参数的变化与不确定性可以归结在动态负载项f中统一进行处理，这是因为系统受到的负载本身就是动态变化且无法精确计算。控制驱动项的系数b与控制器的输出类型有关，一般是确定的，也可以根据实际试验数据计算得到。这样计算出来的模型参数a0、a1、a2和b称之为标称参数，可以代入模型进行实时运算。值得注意的是，在模型推导过程中a0是零，但在实际离线辨识时仍将其作为未知参量进行处理。

通过RBF 神经网络对动态负载项f进行在线辨识，实际辨识的f除了与上述表达式中的负载力和阻力有关外，还应该与其它不确定项和未建模项有关。值得一提的是这里的f实际是负载力和阻力的微分，因此本文的RBF 具有超前观测负载力和阻力的特点，对减小位置跟踪控制的滞后有好处，这一点在后文的仿真与实验中得到了印证。

离线辨识采用的激励信号为组合的正弦信号，所辨识系统的输入信号为PWM 信号，输出信号为俯仰缸位移信号，使用MATLAB 辨识工具箱辨识后，得到模型参数的值为a0= -1.5、a1= -82.25、a2= -22.8631、b= 16.108 85。

2 RBF 神经网络的结构

RBF 神经网络是一种单隐层的三层前馈网络，其基本结构如图3所示。该神经网络具有良好的逼近能力和泛化能力，对于f构建了一个动态系统，在控制的过程中引入RBF 神经网络对其进行建模，构建的动态系统能够在机械臂的控制过程中逐步迭代，逼近控制系统的动态负载项。

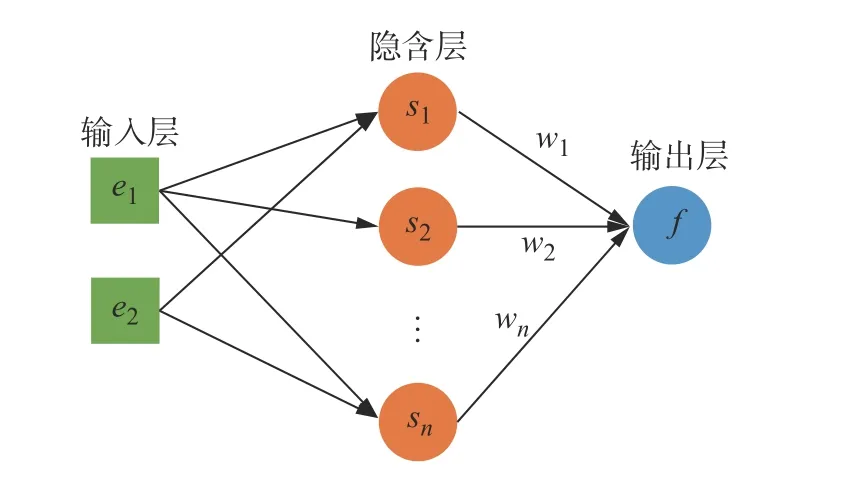
图3 RBF 神经网络结构Fig.3 RBF neural network structure

RBF 神经网络的输出形式为

式中：X为二维网络输入向量，X=[e1,e2]T，e1、e2分别为液压缸位移和速度的跟踪误差，通过控制反馈获得；W为输出层的权向量，W=[w1,w2,···,wn]T；S（X）为径向基函数向量，S(X)=[s1,s2,···,sn]T，n为隐含层节点数；ε为逼近误差。通过采集实时控制过程中的变量的控制偏差，在控制的动态过程中不断调整网络参数，以达到实时逼近f的目标。

径向基函数选为高斯函数，即

式中：Cj为第j个节点的中心向量，Cj=[cj1,cj2]T；bj为高斯函数的带宽。当输入为0（即控制达到稳态以后）时，RBF 网络的输出为一确定值。

将网络的权值向量和径向基函数向量的估计值记为Wˆ 和Sˆ，神经网络输出的近似值可表示为

定义所有节点中心向量C=[C1,C2,···,Cn]T，其估计值为Cˆ ， 高斯函数的带宽向量B=[b1,b2,···,bn]T，其估计值为Bˆ。通过建立一个网络参数更新的动态系统，在控制过程中不断更新网络参数以逼近f。网络参数的更新律推导和计算过程详见第4 节，其形式如下：

式中： Γ1、 Γ2、 Γ3为对角增益矩阵；μ1、μ2、μ3均为修正项系数，µ1>0 、µ2>0 、 µ3>0；e3为加速度的跟踪误差，是网络参数更新的一个重要依据，通过控制反馈获得。

3 反步控制器设计

本文使用反步法完成机械臂控制器的设计，反步控制是一种非线性控制算法，是根据系统的状态方程依次构造Lyapunov 函数，通过推导每个状态变量的虚拟控制律最终递推获得整个系统的控制律的方法。控制器依据建模和辨识所获得的系统模型建立，所设计的控制系统结构如图4 所示。

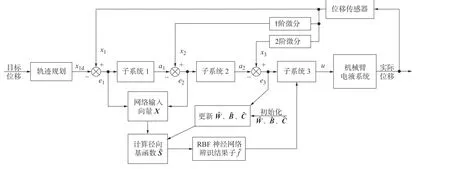
图4 RBF 神经网络反步控制系统结构Fig.4 RBF neural network's backstepping control system

该控制系统（图4）首先根据液压缸的目标位置进行轨迹规划，获得期望位移轨迹x1d，然后通过反步控制的推导过程，建立3 个依次递推的虚拟控制律，最终获得系统的控制输出u。系统的目标是进行位置跟踪，子系统1 是根据位置跟踪的偏差（e1）得到期望的活塞运动速度α1，子系统2 是根据活塞运动的速度偏差（e2）获得其期望加速度α2，子系统3 是根据活塞运动的加速度偏差（e3）和系统模型获得最终的控制率律u。在实时控制系统中除了使用传感器的位移测量值（x1）外，还用到了其速度（x2）与加速度（x3）的值，为了减少微分运算产生的噪声，本文在实验中引入了跟踪微分器求取微分。为了减少文章篇幅，此处未对跟踪微分器的设计进行描述。

最终的反步控制器的输出中包含了RBF 神经网络的计算结果。此处的RBF 是一个实时迭代的动态过程，对RBF 的参数初始化以后，根据控制过程中的跟踪误差e1、e2便可以计算出RBF 的输出fˆ（式（5））；RBF 的参数更新按照式（6）～ 式（8）引入了加速度跟踪误差e3；大量仿真与实验证明，这样构成的RBF 动态更新系统可以获得非常好的实际效果。

反步控制律的设计过程如下。定义每个状态变量与期望值之间的跟踪误差为e1、e2、e3，其表达式为：

式中：x1d为目标位移；α1、α2为虚拟控制量，分别为期望的速度与加速度。

根据系统的状态方程（式（2）），构建3 个子系统；依次运用Lyapunov 稳定条件，得到子系统的虚拟控制量，逐步反推到最终的实际控制律；这样的3 个子系统通过串级连接，最终自然能够保证系统的稳定条件。

1）最外环为位移控制，定义第一个子系统的Lyapunov 函数为

由式（14）可知，若误差e2有界且在原点附近收敛，则该导函数小于0，即第一个子系统稳定。

2）考虑速度环，定义第二个子系统的Lyapunov函数为

同样可以看出，若误差e3有界且在原点附近收敛，则该导函数小于0，即第二个子系统稳定。

3）针对最内的加速度环，定义第三个子系统的Lyapunov 函数为

式中k3>0为可调节增益。这样通过前两步的推导，最后可以得到实际可以操控的控制量，并能保证系统稳定。在实际控制量计算中，动态负载这部分采用的是实时估计值（即RBF 的输出）。可见RBF的收敛性对系统的稳定性起到很大的影响。

4 RBF 更新率设计和控制系统稳定性分析

4.1 更新率设计

定义网络权值的误差向量和径向基函数的误差向量分别为W˜=W-Wˆ 、S˜=S-Sˆ，则神经网络的逼近误差为

定义所有节点中心的误差向量为C˜，径向基函数带宽的误差向量为B˜，通过泰勒级数展开可以将每个径向基函数的误差转换为部分线性形式，即

式中vj为高阶项，j=1,2,···,n。

则径向基函数可表示为

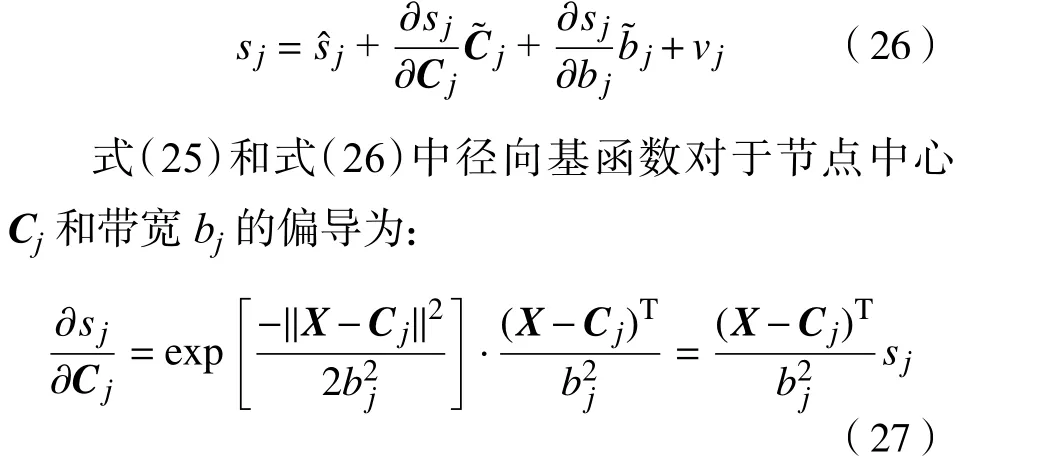
为了保证系统的稳定性，使所有跟踪误差收敛至零，根据式（33）可以写出神经网络的更新律，其结果为式（6）～式（8）。

4.2 稳定性分析

综合上述设计的反步控制器及RBF 神经网络，下面给出整个控制系统的稳定性分析。

将式（6）～式（8）代入式（33）中，可得

5 仿真与实验

5.1 仿真分析

为了验证本文提出的控制方法的有效性，在MATLAB/Simulink 中搭建仿真平台对机械臂的电液系统进行控制仿真，使其液压缸跟踪给定的期望位移轨迹。仿真中电液系统的模型和控制算法均通过s函数实现。仿真模型框架如图5 所示。

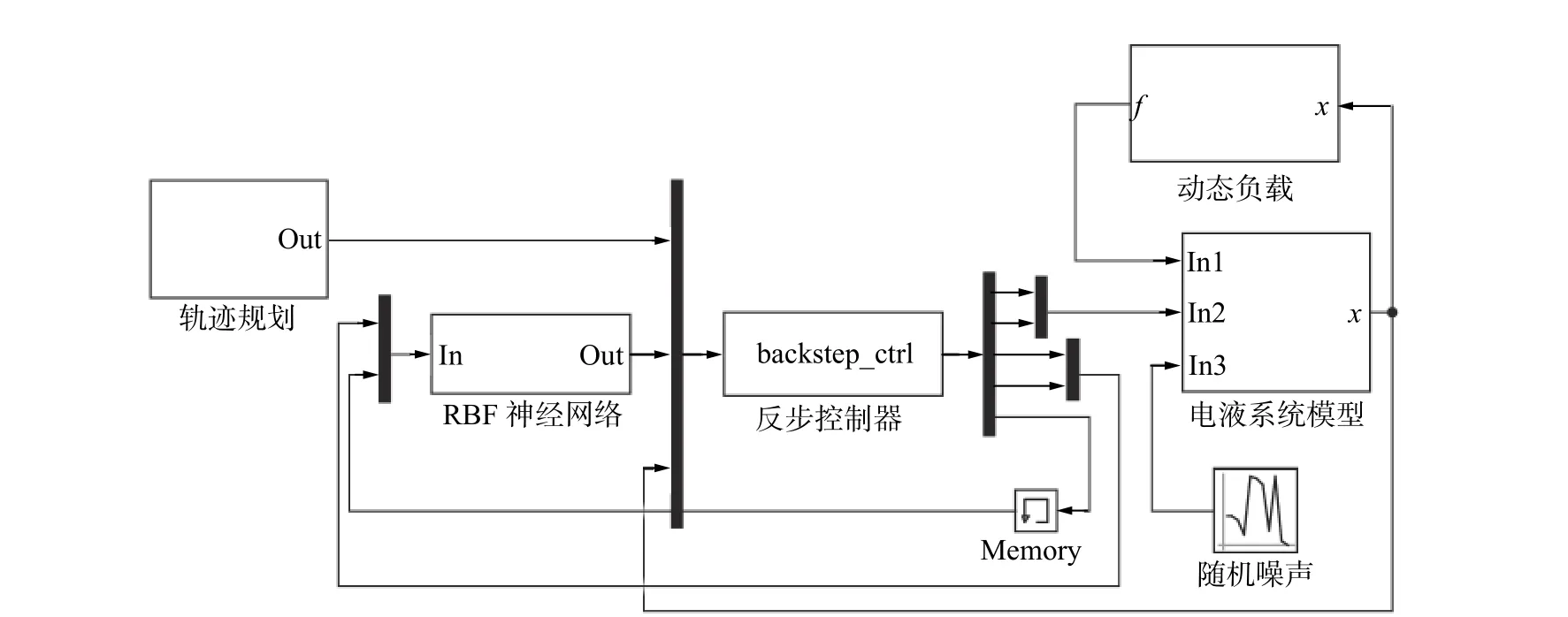
图5 锚杆钻车机械臂电液系统仿真模型Fig.5 Simulation model of bolt drilling truck manipulator of an electro-hydraulic system

仿真模型中的各个参数如表1 所示。

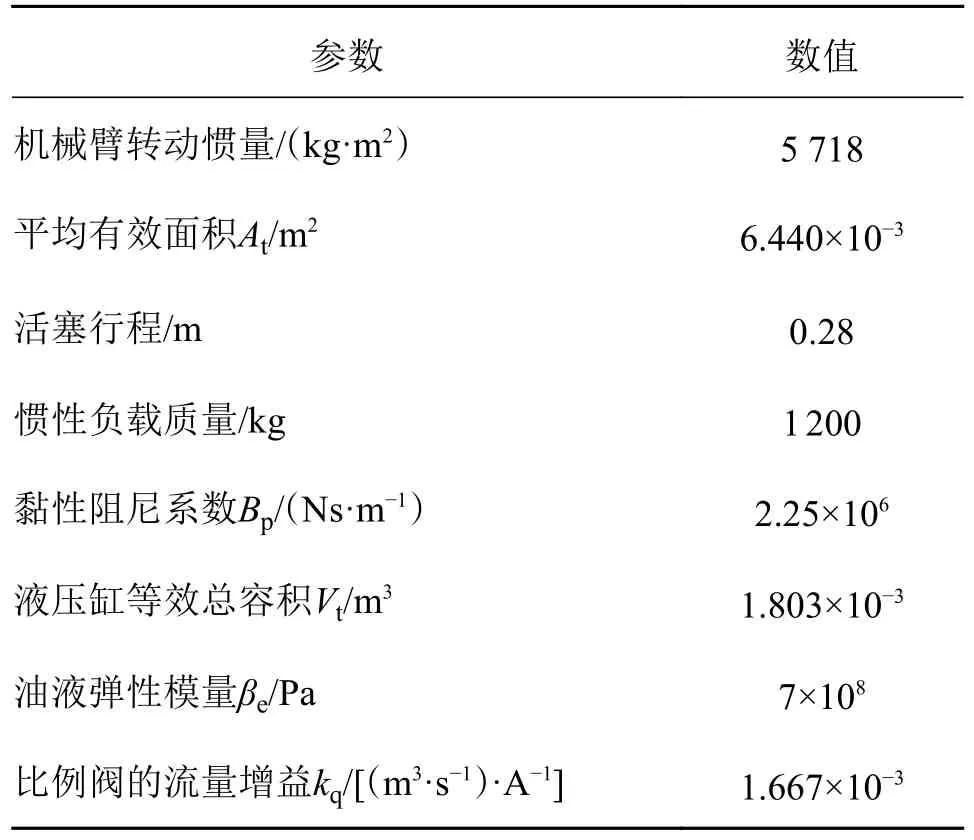
表1 机械臂电液系统参数表Tab.1 Manipulator's electro-hydraulic system's parameters

仿真中添加系统中的动态负载项，并在输入中加入随机噪声。液压缸位移的期望轨迹选为五次多项式和正弦信号两类。

反步控制器的控制参数n1=18、n2=14、n3=12，RBF 神经网路节点数n= 5，神经网络输出权向量初值W=[0 0 0 0 0]T，高斯函数的带宽向量的初值B=[1 1 1 1 1]T，修正项系数 µ1=µ2=µ3=0.2，对角矩阵增益为 Γ1=Γ2=Γ3=diag(15 15 15 15 15)，节点中心向量的初值设为

将本文设计的RBF 神经网络反步控制与工业中最常用的PID 控制进行仿真对比，PID 的比例增益为Kp=500， 积分增益取Ki=50， 微分增益取Kd=10。五次多项式是一类加速度连续的轨迹，可以减少惯性负载对系统的不利影响，适用于重型机械臂的位置跟踪控制；正弦信号相比五次多项式是一类快速变向的信号，对于机械臂的电液系统而言，跟踪正弦信号更能反映出控制器的性能。五次多项式轨迹跟踪的仿真结果如图6 ～ 图9 所示，正弦轨迹跟踪的仿真结果如图10 ～ 图13 所示。

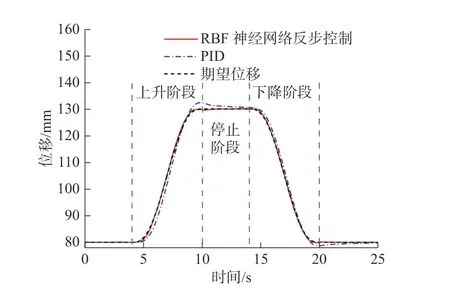
图6 五次多项式轨迹位置跟踪仿真Fig.6 5th polynomial trajectory position tracking simulation

由图6 可知：RBF 神经网络反步控制相比PID 具有更好的跟踪性能，PID 控制会产生较大的超调，且跟踪曲线明显滞后于期望曲线。由图7 可知：RBF 神经网络反步控制将最大跟踪误差由PID 控制的3.55 mm 降低至1.02 mm，且缩短了调整时间，可以使系统更快达到稳态值，跟踪的实时性和准确性较PID 有很大提升。由图8 可知：PID 控制器的输出信号的幅值也大于RBF 神经网络反步控制器输出，如果减小PID的增益，可以减小控制器输出，但其跟踪误差及滞后性将会更大。图9 为跟踪五次多项式时神经网络对模型中动态负载项的辨识结果，该结果与仿真中人为添加的动态负载项基本一致，说明RBF 神经网络可以准确辨识出模型中的动态负载项。

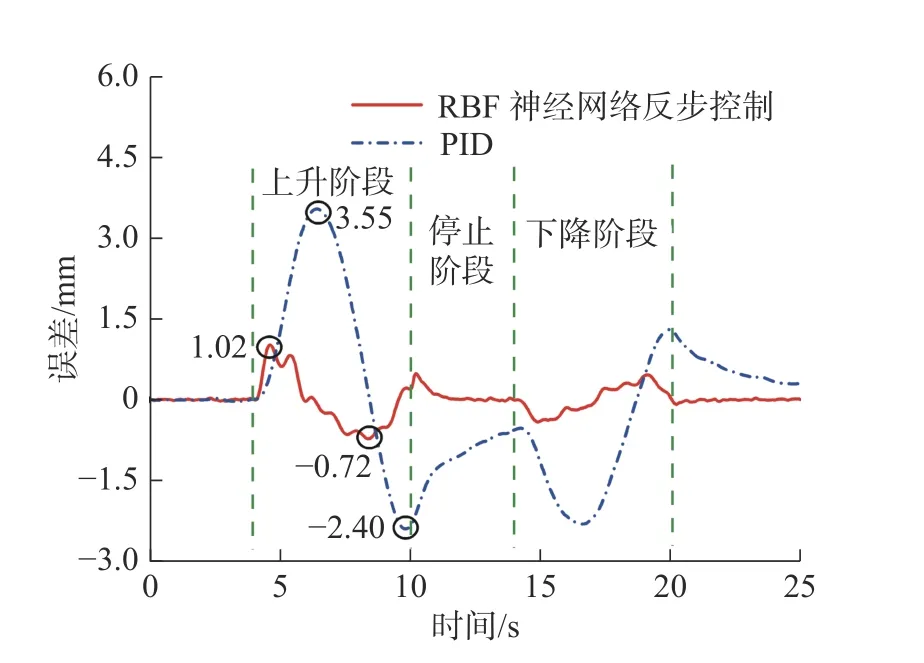
图7 仿真图6 对应的位置跟踪误差Fig.7 Position tracking error in Figure 6

图8 仿真图6 对应的控制器输出Fig.8 Controller output in Figure 6

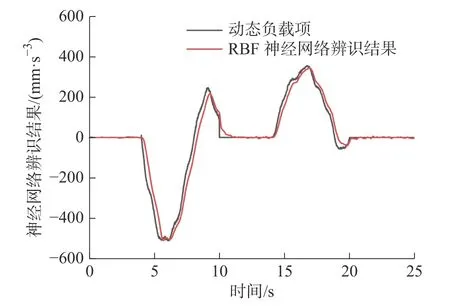
图9 仿真图6 对应的神经网络的输出Fig.9 Neural network output in Figure 6

由图10 和图11 可知：在仿真跟踪正弦信号时，PID 控制的跟踪误差较大且存在较大波动，误差的最大值达到了8.36 mm；RBF 神经网络反步控制的跟踪误差的最大值为3.51 mm，在跟踪精度上较PID 有了很大的提升。图13 是跟踪正弦信号时RBF 神经网络对机械臂电液系统模型中动态负载项的辨识结果，该结果表明对于仿真中人为添加的动态负载项，RBF 神经网络的输出可以实时跟随动态负载项的变化。

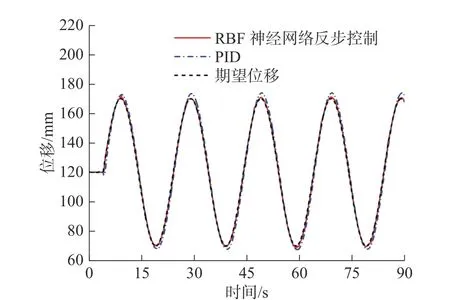
图10 正弦轨迹位置跟踪仿真Fig.10 Sinusoidal trajectory position tracking simulation

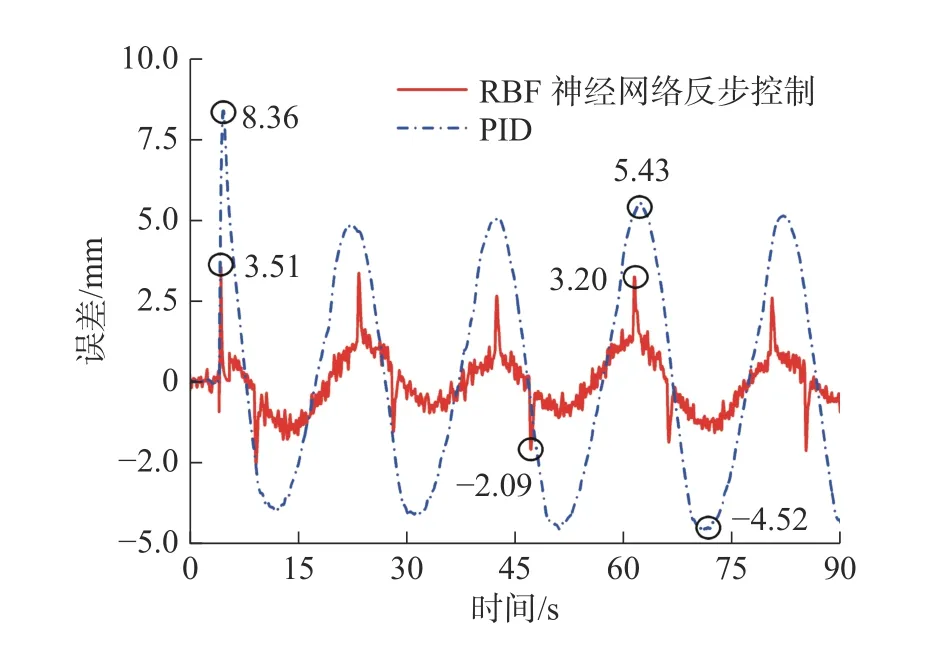
图11 仿真图10 对应的位置跟踪误差Fig.11 Position tracking error in Figure 10

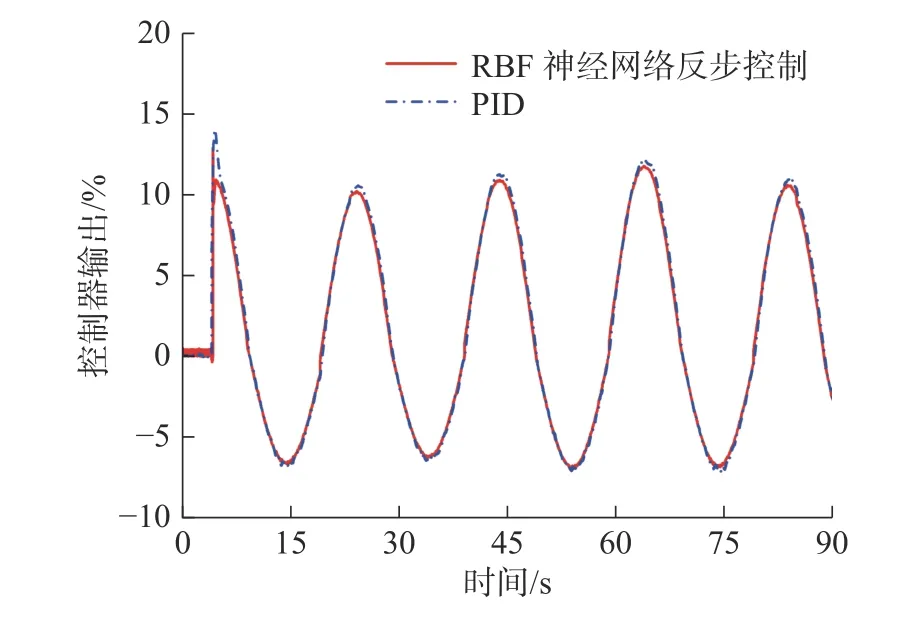
图12 仿真图10 对应的控制器输出Fig.12 Controller output in Figure 10

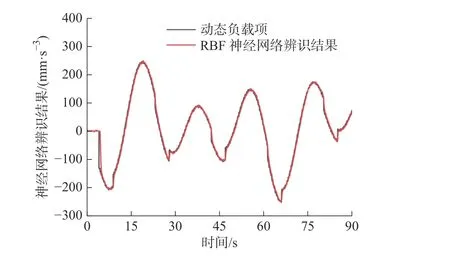
图13 仿真图10 对应的神经网络的输出Fig.13 Neural network output in Figure 10

5.2 实验及结果分析

实验平台如图14 所示，整个系统由上位机电脑进行监控，下位机的控制器为EPEC 5050 型号的PLC，控制器向比例换向阀输出的控制信号为PWM信号，控制系统的采样间隔为10 ms，通过控制信号调节比例换向阀的开度，驱动液压缸运动，所控制的液压缸为机械臂的大臂俯仰缸，行程为280 mm，实验设备为煤矿用液压锚杆钻车，液压缸的位移信号通过传感器反馈获得。

图14 锚杆钻车机械臂实验平台Fig.14 Bolt drilling truck's manipulator experimental platform

俯仰缸是驱动整个机械臂升降的油缸，在运动过程中受到的负载变化较大，极易使机械臂发生卡顿、抖动等问题，因此对控制器的性能有着较高的要求。实验时分别使用本文设计的RBF 神经网络反步控制算法和PID 控制对锚杆钻车机械臂的俯仰缸进行运动控制。由于比例阀存在死区，对其进行静态补偿，俯仰缸上升时的静态补偿量为34%，下降时的静态补偿量为32%。图15 ～ 图17 为五次多项式轨迹的跟踪结果，图18 ～ 图20 为正弦轨迹的跟踪结果，表2 和表3 为两种控制方法的实验误差对比。

表2 五次多项式轨迹位置跟踪实验误差对比Tab.2 5th polynomial trajectory position tracking experimental error comparison mm

图15 为两种控制器控制俯仰缸跟踪五次多项式的位移曲线，实验时俯仰缸位移经过上升、停止和下降3 个阶段，最终回到初始位置。采用PID 控制时，由于受到负载、摩擦和死区的影响，跟踪曲线存在明显的滞后，且在进入停止阶段前出现运动不连续现象，导致整个机械臂发生抖动和卡顿；采用RBF 神经网络反步控制时，系统的响应速度显著提高，在启动和停止阶段可以平稳过渡，避免了抖动和卡顿带来的不利影响。

由图16 可知：RBF 神经网络反步控制相比PID 控制具有更高的跟踪精度，PID 控制俯仰缸进入停止阶段时仍具有较大的误差，进入稳态的速度较慢。表2 将两种控制器跟踪五次多项式的误差进行了比较，其中PID 控制的均方根误差为2.43 mm，稳态误差为0.85 mm，而RBF 神经网络反步控制的均方根误差仅为0.73 mm，稳态误差为0.17 mm，该控制方法相比PID 控制提高了系统的控制精度。

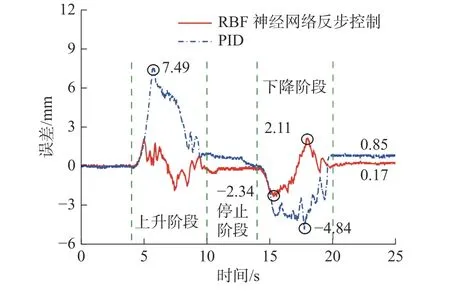
图16 实验图15 对应的的跟踪误差Fig.16 Position tracking error in Figure 15

由图17 可知：RBF 神经网络反步控制相比PID 的控制器输出更小，且更加平稳。本文设计控制器保证了控制器输出的连续性，且对系统施加的控制量比PID 控制更小更加平稳。

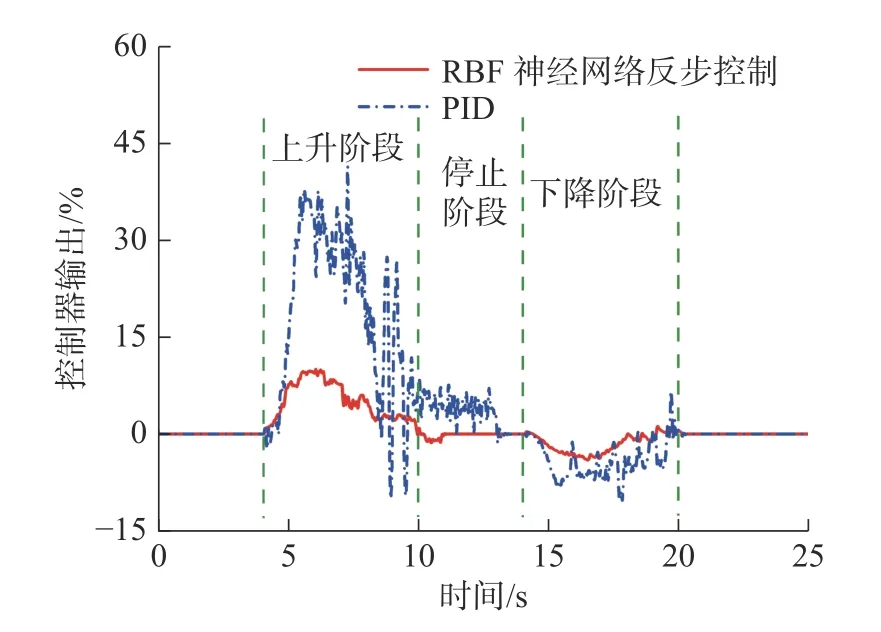
图17 实验图15 对应的控制器输出Fig.17 Controller output in Figure 15

图18 为RBF 神经网络反步控制和PID 控制这两种控制器控制俯仰缸跟踪正弦信号的位移曲线。由图18 和图19 可知：在启动阶段俯仰缸存在跟踪滞后的问题，采用 PID 控制的最大滞后误差为12.14 mm，均方根误差为3.66 mm，采用RBF 神经网络反步控制的最大滞后误差为7.93 mm，均方根误差为1.39 mm，RBF 神经网络反步控制减小了跟踪的滞后误差，提高了系统对正弦轨迹的跟踪能力。由图20 可知：跟踪正弦信号时PID 控制器的输出信号会出现较大的波动，而使用RBF 神经网络反步控制器的输出信号波动较小，整体的输入量也更小。表3将两种控制器跟踪正弦信号的误差进行了对比，结果表明本文设计控制器的控制效果优于PID 控制。

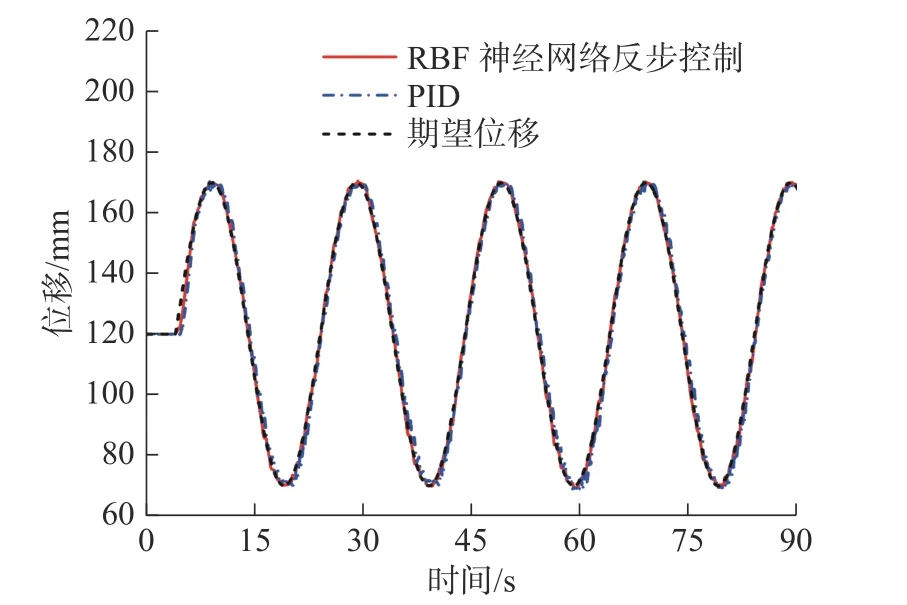
图18 正弦轨迹位置跟踪实验结果Fig.18 Sinusoidal trajectory position tracking experimental results

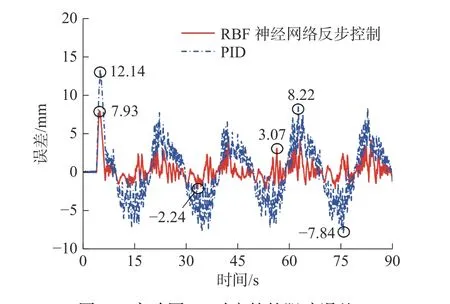
图19 实验图18 对应的的跟踪误差Fig.19 Position tracking error in Figure 18

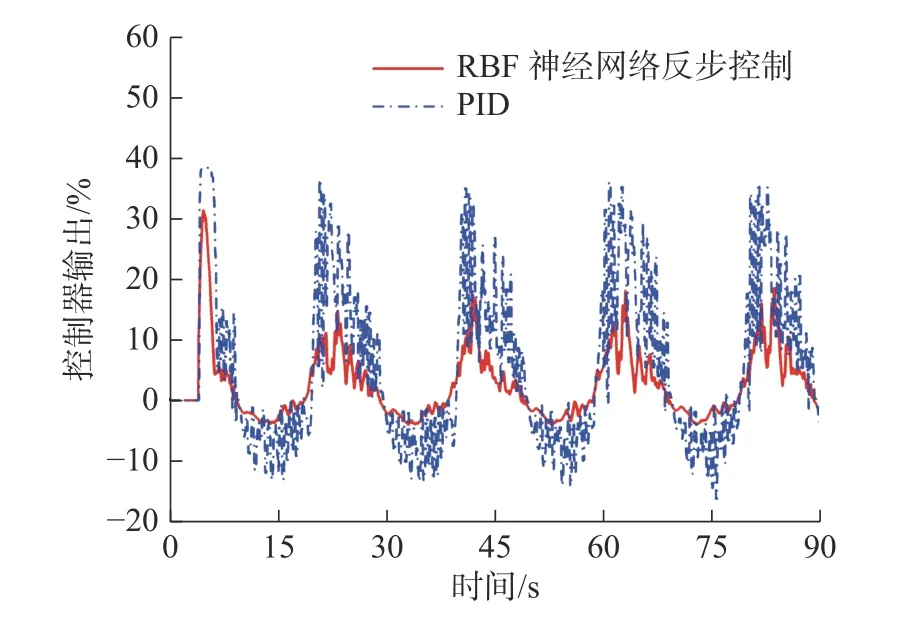
图20 实验图18 对应的控制器输出Fig.20 Controller output in Figure 18

实验结果表明，本文设计的RBF 神经网络反步控制相比PID 控制具有更好的控制性能。该控制方法的控制输出更加平稳，可以提高机械臂对期望轨迹的跟踪能力，并保证系统具有较高的控制精度。

6 结论

为了提高重型机械臂电液驱动系统的控制精度，以某煤矿用锚杆钻车的液压驱动机械臂为研究对象，设计了一种反步控制器，并引入了RBF 神经网络辨识动态负载。仿真与实验证明是一种有效的解决方案，得到以下结论：

1）电液系统中的参数不确定问题，考虑到参数变化的缓慢性，可以采集试验数据，通过离线辨识得到标称参数，其时变部分可以纳入动态负载项。

2） 反步控制器与RBF 神经网络有机结合是一种有效的控制结构。本文的反步控制器分为位置子系统、速度子系统和加速度子系统，这3 个子系统串级连接，可以得到最终的控制律；这3 个子系统还为RBF 神经网络提供了实时的输入向量和参数更新驱动；RBF 神经网络可以得到时变的动态负载估计，提供给控制器计算控制输出。

3） 本文的动态负载辨识是在负载力和阻力的微分层面上进行的，实时辨识的结果对负载变化较为敏感，可以提高动态负载估计的实时性和系统的响应速度。

4） 本文控制算法的设计原则是Lyapunov 稳定性理论，控制律的推导和RBF 神经网络参数更新率的推导均以稳定性理论为基础，与PID 控制相比，该算法能够有效的提高系统的位置跟踪精度，满足工程上的应用要求。