用于汽车门锁的多运动模式空间柔顺开启机构及稳定性分析

钟传磊，杭鲁滨 , ，王明远，曲志洋

（1.上海工程技术大学 机械与汽车工程学院，上海 201620；2.上海市大型构件智能制造机器人技术协同创新中心，上海 201620）

汽车门锁作为车门系统内部一个重要的安全部件，其功能可靠性及稳定性与乘客使用体验及安全息息相关。图1 为高端汽车侧门锁多支链机构示意图，汽车门锁由执行模块、操动模块组成。执行模块主要由棘轮、棘爪和复位弹簧构成[1]，实现汽车侧门上锁与解锁功能；操作模块主要由刚性连杆、弹簧、限位块以及运动副组成的刚柔耦合机构支链[2]构成，其多条支链实现汽车门锁不同功能需求。

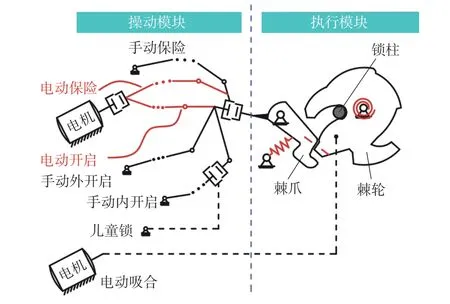
图1 高端汽车侧门锁多支链机构示意图Fig.1 Schematic diagram for the interior mechanisms of a vehicle's side door latch

汽车门锁内部各支链机构的设计理念涵盖机构学、齿轮传动以及间歇动力学等[3]。Udriste 等[4]以新型门锁功能分解角度，进行汽车门锁内部支链的变自由度变拓扑机构特征分析；王炎等[5]提出一种可实现电动开启功能的解锁运动链并进行轨迹综合确定机构尺寸。

柔顺多运动模式机构[6]可实现多种运动模式的输出，具有机构储能和释放能量的特点，适合多功能需求的应用。Tank 等[7]基于五杆机构与扭簧构造了欠驱动多自由度机构，实现了柔顺变行程运动；尹鹏等[8]利用弹簧能量储存特性，引入刚度调节柔顺机构，实现了足式机器人柔顺关节刚度可调；王明远等[9]提出新型柔顺副，构造了多种运动模式变自由度五杆机构作为电动开启支链，实现汽车门锁多工况。

柔顺机构嵌入汽车门锁内部以多运动模式完成各工况下功能需求，但引入非线性运动特征[10]，导致锁内各支链运动周期轨迹的重复性差，乃至将引起各支链扫掠空间瞬时交叉，甚至各支链运动干涉，难以保证汽车门锁的安全性和功能稳定性。各支链周期轨迹重复性可视为汽车门锁内部运动稳定性问题。

最大Lyapunov 指数分析是研究欠驱动柔顺机构运动稳定性的重要方法之一[11]，表征了系统在相空间中相邻轨迹间收敛或发散的平均指数率[12]。基于最大Lyapunov 指数的数值计算方法[13]，Erkaya 等[14]将间隙机构与柔顺机构进行对比，分析关节间隙对于系统输出稳定性影响；侯雨雷等[15]以最大Lyapunov指数判别机构的混沌运动,并研究不同间隙大小及输入速度对机构混沌运动状态的影响。

本文基于新型柔顺副构造了用于汽车门锁的多模式空间柔顺机构；分析了该机构的模式切换、运动特征点稳定性等特性；以最大Lyapunov 指数为机构稳定性评价指标，基于Wolf 法计算特征点位移序列的最大Lyapunov 指数，优选柔顺副扭簧刚度，保证新型空间柔顺机构在车门锁内稳定运行。

1 多模式空间柔顺机构RRPRSR

不同于平面机构，空间机构可实现三维轴向传动，布置灵活，具有灵活有效使用空间、工作灵活可靠、运动多样等特点，在狭窄受限空间的布置尤其具有优越性。

基于以上特点，提出一种多模式空间柔顺机构作为汽车门锁电动开启支链，需要满足以下特征：

1）根据不同原动件及限位情况，灵捷运用汽车门锁内空间，多支链多运动模式实现汽车门锁多种工况。

2）汽车门锁多支链共用驱动，电动开启支链作为主要传动支链，其扫掠空间与其他支链互不干涉，各工况下互相兼容。

1.1 多模式空间柔顺机构RRPRSR 的构造和应用

本研究团队前期所提出一种具有力适应复位特性与约束变化特性的新型柔顺复合副[9]，如图2 所示，其由含槽连杆、滑块连杆、扭簧组成，形成转动副、移动副、扭簧力约束组合的柔顺复合副，旋转中心为G。C、F分别为旋转轴心G在移动副滑槽内左右运动限位端点。移动旋转复合柔顺副由于受C、F的位移限位与扭簧的柔性力约束复位作用，具有变自由度特征、柔顺力复位特征。

图2 新型柔顺副示意图Fig.2 Schematic diagram of a novel compliant joint

基于柔顺副构造的新型多模式空间柔顺机构RRPRSR 如图3 所示，嵌入到汽车门锁内作为电动开启支链的实际应用如图4 所示。

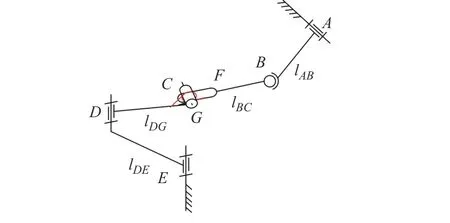
图3 多模式空间柔顺机构简图Fig.3 Schematic diagram of a multi-mode spatial compliant mechanism

图4 多模式空间柔顺机构锁内应用Fig.4 Application of spatial compliant mechanism with multi-mode motion to the vehicle's side door latch

空间柔顺机构所构造汽车门锁机构简图如图5所示，汽车门锁机构主要由电动开启支链与保险支链构成。其中电动开启支链需按时序操控电动开启与保险支链使棘爪转动，实现棘轮脱离锁柱即汽车门锁解锁功能；保险支链衔接电动开启支链与棘爪，起到离合作用。

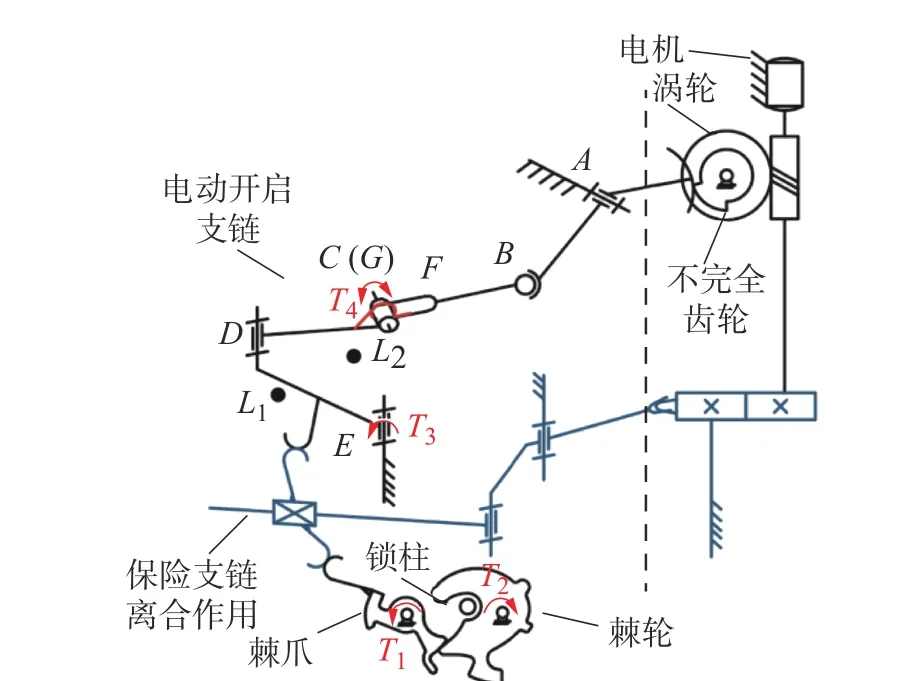
图5 空间柔顺机构所构造汽车门锁机构简图Fig.5 Schematic diagram of the vehicle's side door latch's interior mechanisms constructed with the spatial compliance mechanism

图5 中：T1～T4为扭簧产生的力矩；T2作用于棘轮上，为汽车门锁开启提供回复力；T1、T3分别作用于棘爪盘、棘爪上，为汽车门锁机构提供复位力，是开启门锁需要克服的力；T4作用于柔顺副旋转轴上，具有姿态回复保持作用，实现力顺应特征；L1与L2为锁内限位挡块；DE杆在L1与L2范围内运动，DE杆初始位置与L1限位块接触。

1.2 多模式空间柔顺机构RRPRSR 运动模式分析

多模式柔顺空间机构RRPRSR 依据锁内工况、驱动以及限位约束的不同，具有RSRRR 运动模式、RRPRSR 运动模式和RRPRS 运动模式和RRRP 运动模式。多模式空间柔顺机构4 种运动模式在汽车门锁多工况的应用说明，如表1 所示。

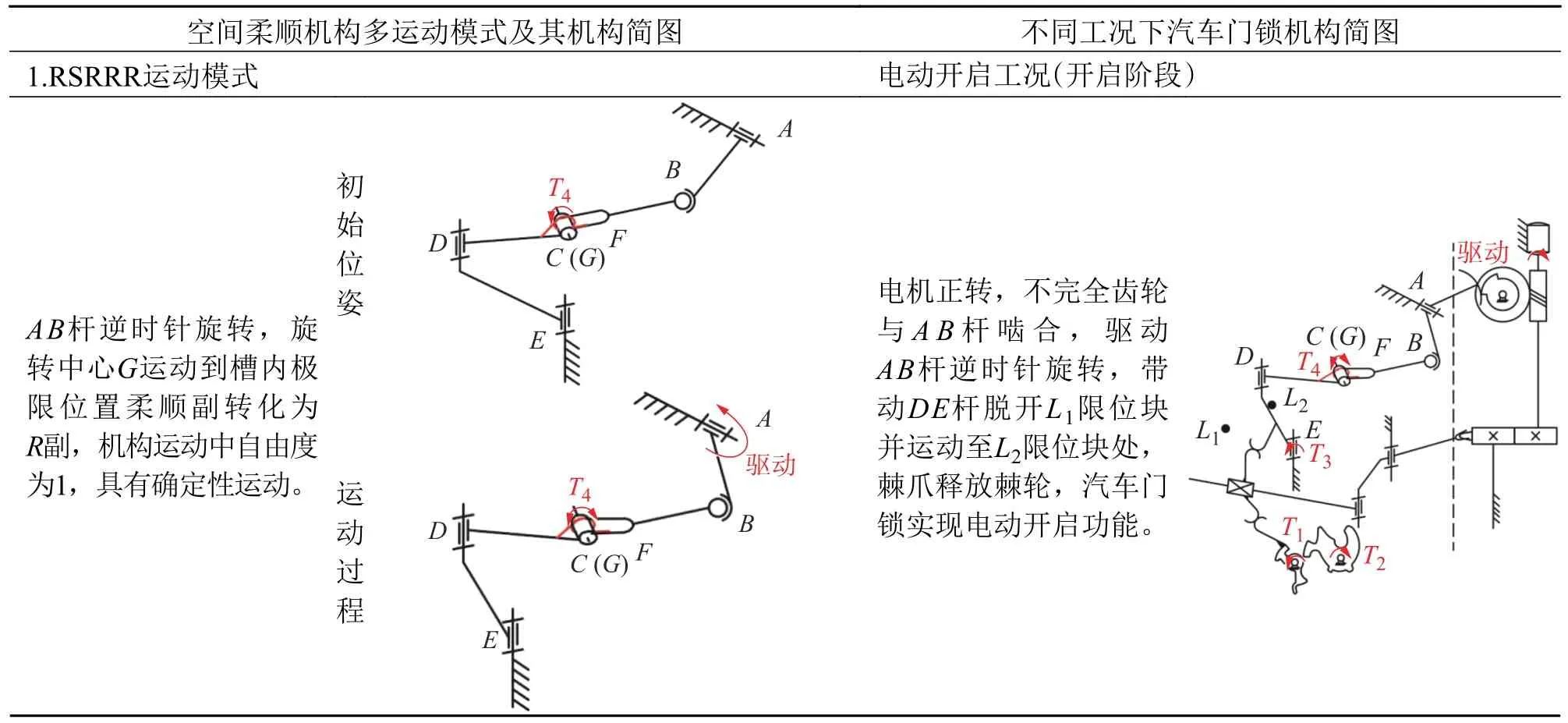
表1 各工况空间柔顺机构过程及其对应的车门锁机构运动Tab.1 Kinematical representation and relationship between vehicle's side door latch and spatial compliant mechanism under various working modes

其中，机构RSRRR、RRPRS 与RRRP 运动模式由于限位与机构刚化等情况，实现自由度为1 的确定性运动；机构RRPRSR 运动模式具有2 个自由度，在柔顺副扭簧力约束条件下实现力自适应性复位。

多模式空间柔顺机构尤其适用于汽车门锁狭小空间内部实现多种工况，其柔顺性满足电动开启支链与保险支链的兼容性。

2 多模式空间柔顺机构动力仿真分析

多模式空间柔顺机构RRPRSR 嵌入门锁装置构造高端汽车门锁多功能支链；在电动开启回复阶段中，机构处于欠驱动工况，其运动学回路方程数少于变量数，需联立动力学方程组求解，而其方程组形式为2 阶代数偏微分方程，模型解析求解尤为困难。故需通过ADAMS 软件建立汽车门锁三维模型，仿真分析多模式空间柔顺机构RRPRSR 的运动性能及动力学性能。

2.1 多模式空间柔顺机构RRPRSR 动力学仿真

针对汽车门锁大密封力300 N 要求，以门锁样机的尺寸参数及运动参数进行动力学仿真，验证多模式空间柔顺机构应用于汽车门锁的可行性和稳定性。

在ADAMS 软件中建立的汽车门锁的仿真模型如图6 所示，其中红色虚线为电动开启支链，蓝色虚线为保险支链。

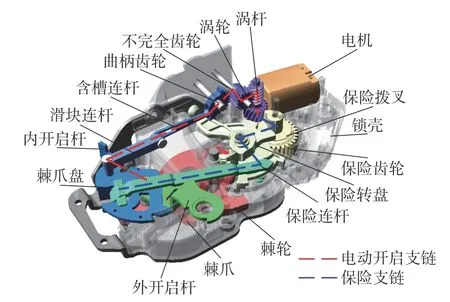
图6 多模式空间柔顺机构构造的汽车门锁仿真模型Fig.6 The simulation model of the vehicle's latch constructed with the spatial compliance mechanism

由多模式空间柔顺机构构造的汽车门锁电动开启支链仿真参数如表2 所示。

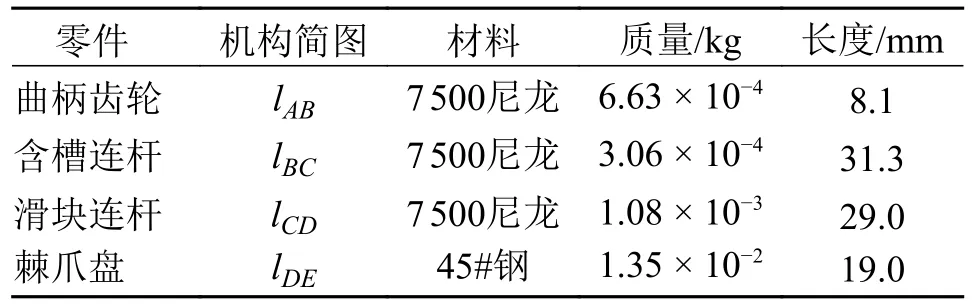
表2 空间柔顺机构几何和物理参数Tab.2 Geometric and physical parameters of the spatial compliant mechanism

机构各弹簧参数的设置如表3 所示，根据文献[16]，设新型柔顺副扭簧刚度为1 N·mm/°，其具体优选取值将在机构稳定性章节讨论。

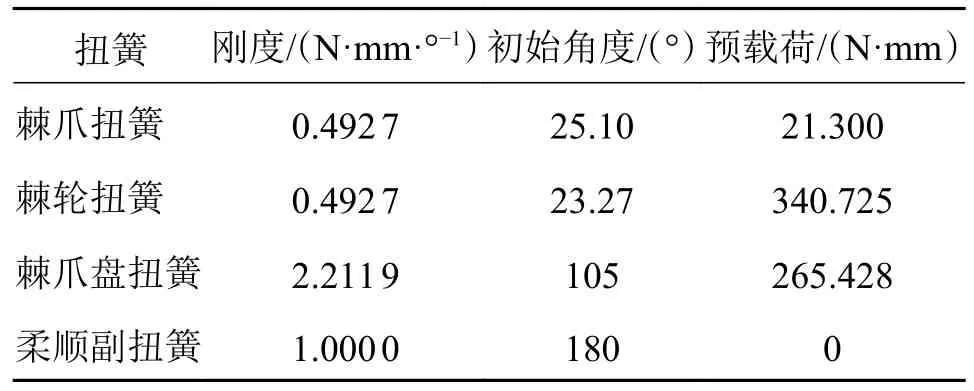
表3 门锁机构内部扭簧参数设置Tab.3 Interior torsion springs' parameter design for latch mechanism

通过汽车门锁在不同工况下的运动仿真，得出汽车门锁内部机构各工况下对应运动模式的驱动时间、运动速度、自由度及驱动力矩如表4 所示。

表4 门锁机构各工况下不同运动模式的运动特性Tab.4 Different motion characteristics of the vehicle's side door latch under different working modes

分析多模式空间柔顺机构在门锁执行各工况时，表现出不同的运动特性，发现电动开启支链电机驱动力矩最大，运动过程为变自由度运动；其结构上与保险支链耦合，且能实现多种功能，为锁内最复杂、最值得研究的支链。

2.2 空间柔顺机构RRPRSR 轨迹与相图分析

用于汽车门锁的多模式空间柔顺机构RRPRSR满足多支链运动的兼容性，但当机构处于欠驱动状态，柔顺副扭簧引入非线性动力学特性，机构产生非稳定运动特性。故柔顺副动力约束扭簧的刚度kT可作为机构运动稳定性研究的关键参数。

多模式空间柔顺机构的运动稳定性研究选择F点作为运动特征点，主要考虑如下因素：

1）F点位于空间连杆BC上，为柔顺副轴线在滑槽内的运动端点，是多模式空间柔顺机构变运动模式的几何边界。

2）F点为距离柔顺副槽初始位置距离C的最远点，也是机构变自由度的几何边界，能表征具有力柔顺特性的空间几何轨迹。

3）F点的空间轨迹反映了A转动副与B球副的运动约束，同时F点也反映D转动副、E转动副与柔顺副滑槽的运动约束。

电动开启过程中特征点F分段轨迹示意图如图7 所示。

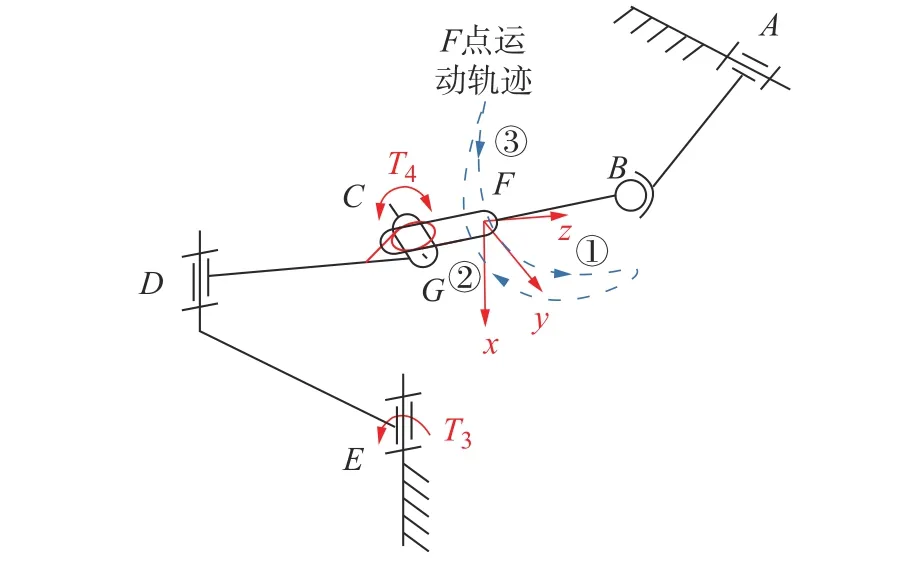
图7 特征点F 分段轨迹示意图Fig.7 Schematic diagram of characteristic point F sectional trajectory

为进一步研究轨迹特性，以点F为原点建立直角坐标系F-xyz，x轴正方向与D转动副轴线平行方向向下，y轴正方向与G点旋转轴平行。图7 中，顺序号和箭头用于表示分段轨迹的顺序和方向。在电动开启工况下，柔顺机构执行单自由度确定运动RSRRR 机构运动模式（分段轨迹①）和欠驱动力自适应复位RRPRSR 运动模式（分段轨迹②和③）。

柔顺副刚度kT为该RRPRSR 机构欠驱动力自适应复位运动模式中提供复位约束力，对该机构工作空间及运动稳定性有较大影响。分别选取kT为0.5 N∙mm/°、1.0 N∙mm/°、1.5 N∙mm/°、2.0 N∙mm/°和5.0 N∙mm/°，以机构特征点运动轨迹进行稳定性趋势研究。ADAMS 软件仿真作出该机构所对应连续10 个运动周期的特征点三维运动轨迹，并根据时间变量用位移矩阵表示三维运动轨迹，记作HF，即

式中：x(ti)为 第ti个 时间点x方向上的位移；y(ti)为第ti个 时间点y方向上的位移；z(ti) 为 第ti个时间点z方向上的位移；N为时间长度。

当轨迹重合度较高时，难以确切分析出具体多模式分段轨迹，而相图是状态空间的轨迹，可描述物体的运动状态。特征点F在不同柔顺副扭簧刚度kT下的轨迹及相应相图如图8 所示。特征点F在不同柔顺副扭簧刚度kT下的轨迹表明，各周期可视化显示整体重合度较高，但在回复阶段RRPRSR 运动模式中存在两个局部混乱区域。结合特征点轨迹图可知，相图中的波动主要来源于特征点速度的变化。

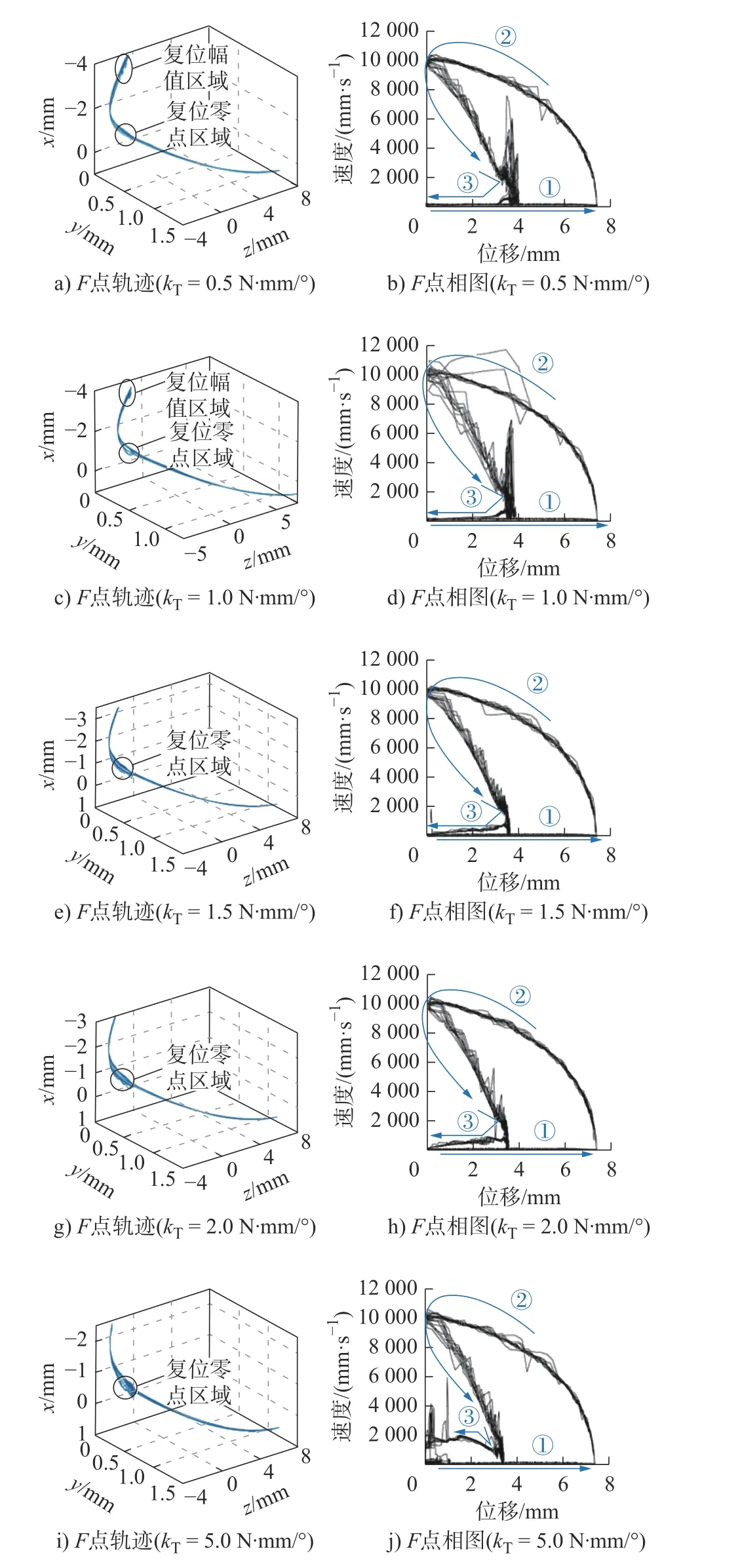
图8 扭簧不同刚度kT 下，特征点F 轨迹与相图Fig.8 Motion trajectories and phases of characteristic point F trajectory with different kT

图8 中轨迹图分析如下：

1）当柔顺副扭簧刚度kT较低时（见图8a）和图8c）），由于该机构复位过程速度较快，扭簧约束力过小，无法在有限运动距离内抵消复位惯性力，在特征点F运动到回复幅值区域时受到冲击，出现局部混乱，但复位零点区域因扭簧约束力较小，机构在到达零点后震动较小，复位零点区域混乱不显著。

2）当柔顺副扭簧刚度kT较大时（见图8e）、图8g）和图8i）），扭簧约束力在有限运动距离内抵消复位惯性力，回复幅值区域局部混乱消失，但复位零点区域因扭簧约束力过大，机构在到达零点后混乱区域逐渐增大。

图8 中相图分析如下：

1）从相图中可清晰看出图7 中3 段分段轨迹特征：分段轨迹①相图重合度较高；分段轨迹②和③为欠驱动力自适应运动模式，相图曲线重合度较低。

分段轨迹③中部即复位缓冲区域在kT取值较小情况下，由于受到冲击速度会有剧烈波动（见图8b）和图8d））；在kT取值较大情况下，由于扭簧约束力大大增加，复位过程中会提供较大复位惯性力，同样会在零点区域造成震动冲击（见图8j））。

3）在kT取1.5 N∙mm/°和2 N∙mm/°情况下，相图稳定程度相比其他情况下较高（见图8f）和图8h）），是合适的取值区域，即关键参数kT选取恰当，将提高系统的稳定程度。机构特征点轨迹稳定特性研究及关键参数kT取值范围确定是该机构研究及应用于门锁装置的重要保障。

3 机构动力系统稳定性指标Lyapunov指数的求解方法

机构特征点运动轨迹及相图稳定程度难以仅仅由运动学参数指标评价，本文提出以带时标连杆特征点三维空间轨迹构造时变特征点位移序列动力学系统，引用动力学系统Lyapunov 指数作为稳定性指标研究机构运动稳定性。

3.1 Lyapunov 指数求解方法

Lyapunov 指数作为现代非线性动力学理论中衡量系统动力学运动稳定特征的一个重要量化指标，可以描述状态空间轨道发散或收敛的平均指数率，其指数大小对应系统稳定性好坏[12]，而Lyapunov指数主要通过动力学方程或时间序列这两种方式获得。

基于动力学方程计算，其计算公式为

式中Lyapunov 指数λ的数值主要由函数F(x)在xi处的雅克比矩阵dF(x)/dx所决定。

空间柔顺机构RRPRSR 整个电动开启过程的动力学系统难以解析表示，Lyapunov 指数无法解析方程式求解。

不同于解析求解Lyapunov 指数， Wolf[14]提出以实验或仿真数据提取一维时间序列，重构相空间，数值求解Lyapunov 指数的方法，可在机构动力学系统方程难以表示时求解最大Lyapunov 指数。

3.2 Lyapunov 指数Wolf 数值求解法

从一维时间序列计算Lyapunov 指数的过程包括相空间重构、演化距离和指数求解等步骤。

1）相空间重构

基于非线性动力学系统，采用延迟坐标法[17]将一维时间序列进行重构相空间[18]S(m,P)∈Rm×P

式中：m为嵌入维数；P为相空间向量长度，P=N-(m-1)τ，τ 为延迟时间，由自相关系数法确定[19]。相空间列向量可表示为

嵌入维数m可通过延迟时间τ与平均周期T求得，表达式为

式中平均周期T由FTT 法求得[20]。

2）相空间距离计算

任意两相点的距离可通过欧式距离dEuc求得，即

相空间内任意两相点之间平均欧式距离为

3）相空间内演化点选取过程

相点距离及相空间内演化距离求解最大Lyapunov指数的Wolf 数值法求解过程示意图，如图9 所示。图中：li为 第i次迭代初始相点距离；l′i为第i次迭代演化距离； θi-1为迭代相点间夹角。在动力系统中选取初始距离相近的两相点，其距离增长随时间呈指数分布。如图中黑线所示作为基准相轨迹s(ti)，蓝线为演化轨迹s1(tni)。

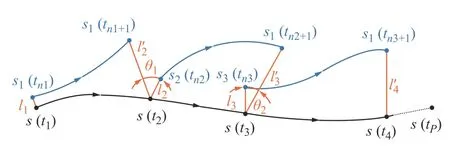
图9 Wolf 数值法求解Lyapunov 过程示意图Fig.9 Schematic diagram of the Wolf method used to solve the Lyapunov exponents

设初始相点为s(t1)，初始相点邻近初始演化相点为s1(tn1)， 两相点之间的距离l1为

式中：s1(tn1+1)和s(t2)分别为时间序列相空间中s1(tn1)和s(t1)的下一点（即演化相点）。

在点s(t2)邻 域范围内搜寻新点s2(tn2)，其迭代过程中搜寻范围需满足距离长度li与 夹角 θi-1取值范围，以减小所搜寻新点由于方向与重叠性导致的误差。搜索条件为：

式中M为总迭代次数。

6）稳定性判别准则

当 λmax＞0 时，动力学系统存在混沌现象，稳定性较低，且λmax越 大，稳定性越低；当λmax＜0 时，动态运动最终趋向于周期运动，稳定性较高；当λmax= 0 时，动态运动为周期性稳定运动，具有良好的运动稳定性，故可选用 λmax作为机构动力系统稳定性指标。

4 最大Lyapunov 指数的机构运动稳定性分析

4.1 电动开启过程机构运动稳定性分析

汽车门锁电动开启过程涉及到多模式空间柔顺机构的变自由度拓扑结构运动、动力演变过程，包括电动开启和复位过程。以最大Lyapunov 指数为机构系统稳定性判别指标，定量分析汽车门锁电动开启工况下多模式空间柔顺机构RRPRSR 运动稳定性。基于Wolf 数值求解法，以电动开启工况下机构特征点F空间周期轨迹曲线进行相空间重构，求解最大Lyapunov 指数。

根据2.2 节所求得的位移矩阵HF，利用欧氏距离将三维轨迹转换为一维时变位移序列d(t)，即

以Wolf 数值求解方法，由式（13）求得对应不同扭簧刚度kT特征点F轨迹位移的最大Lyapunov 指数λmax如图10 所示。以kT=0.5 N∙mm/°为例，其详细参数取值为：m=6、τ=667、P=3 597、N=35 970。从图10 中可看出，在不同弹簧刚度kT下所选取特征点位移的最大Lyapunov 指数最终都收敛于正数。

柔顺副扭簧不同刚度kT下，最大Lyapunov 指数的具体结果如表5 所示。

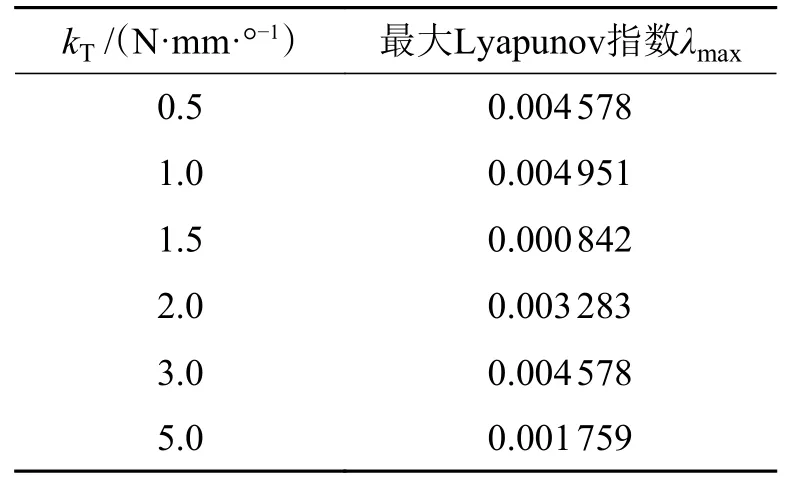
表5 扭簧不同刚度kT 对应最大Lyapunov 指数Tab.5 The largest Lyapunov exponents corresponding to different kT

从 表5 中 可 看 出，kT取1.5 N∙mm/°时，最 大Lyapunov 指数较小，稳定性相较其他取值较高，其结果与2.2 节相图分析相符。

4.2 机构稳定性区域的搜索与发现

为进一步提高该空间柔顺机构机械系统的运动稳定性，在柔顺副扭簧刚度kT= 1.5 N∙mm/°附近区域，插值搜索最优柔顺副扭簧刚度kT取值，以精度ε=10-6计算其最大Lyapunov 指数，以提高空间柔顺机构运动稳定性。

柔顺副扭簧刚度kT插值搜索区域对应的最大Lyapunov 指数结果如表6 所示，当kT= 1.53 N∙mm/°时，其所对应特征点位移的最大Lyapunov 指数最小且在6 位精度下为0，具有良好的运动稳定性。

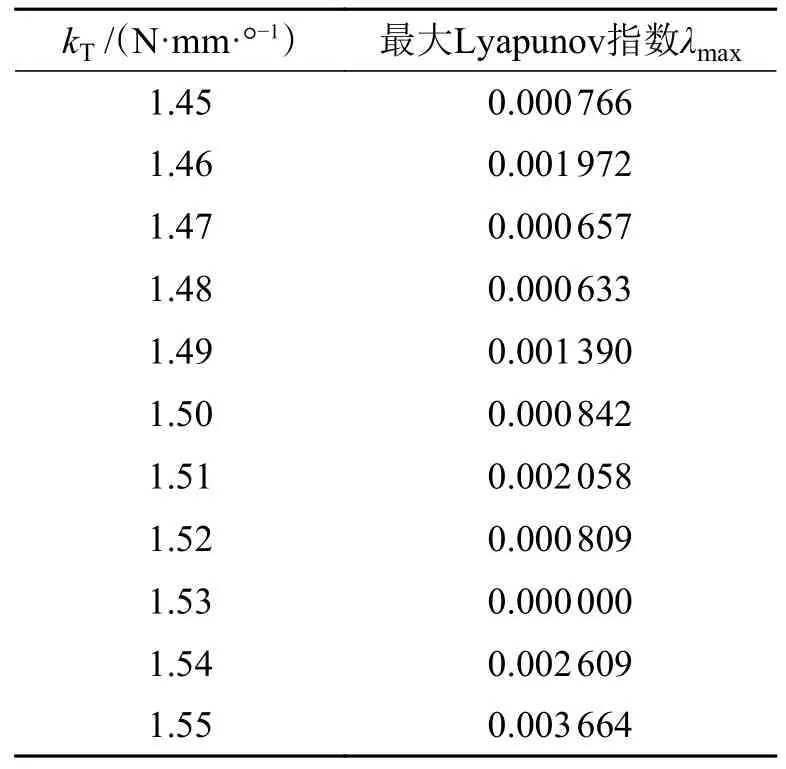
表6 kT 插值搜索区域对应的最大Lyapunov 指数Tab.6 The largest Lyapunov exponents corresponding to additional kT values' search regions

当柔顺副刚度kT= 1.53 N∙mm/°时，所对应机构特征点F的轨迹与相图如图11 所示，其相图在速度方向上虽略有波动，但轨迹曲线重合性较高，在位移方向上较为稳定，与最大Lyapunov 指数作为稳定性指标的判定结果一致。说明kT取1.53 N∙mm/°时，该柔顺机构运动具有较好稳定性，适用于汽车门锁内部电动开启工况。将所求得刚度kT= 1.53 N∙mm/°的扭簧安装于柔顺副，以具有柔顺副的空间柔顺RSRPRR 机构构造门锁样机，如图12 所示，该门锁各工况运动稳定，满足高端多功能汽车门锁电动开启支链需求。

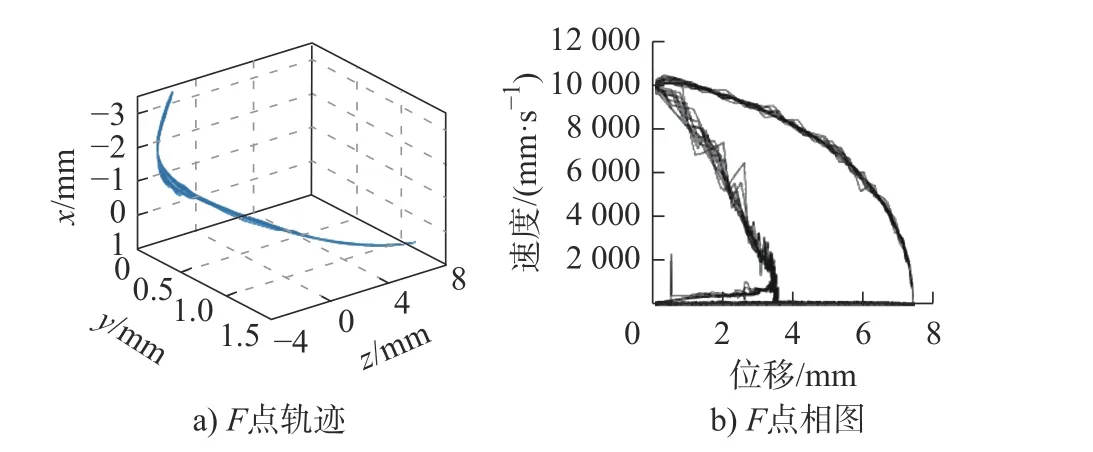
图11 kT =1.53 N∙mm/°时，特征点F 轨迹与相图Fig.11 The trajectory and phase of characteristic point F when compliance joint stiffness kT = 1.53 N∙mm/°

图12 含多模式空间柔顺机构的汽车门锁样机实物Fig.12 Prototype of vehicle's side door latch of the multi-mode spatial compliant mechanism

5 结论

本文构造了一种汽车门锁电动开启支链的多模式空间柔顺机构，以轨迹与相图定性判断，结合最大Lyapunov 指数定量分析的方法，对其运动稳定性进行了优化分析，得出以下结论：

1）基于新型柔顺副提出并构造了一种具有多运动模式的空间柔顺机构。该空间柔顺机构可实现4 种运动模式，以满足高端汽车门锁多功能需求并与其他支链互相兼容。

2）Adams 仿真得出了空间柔顺机构相图与轨迹，定性判断了柔顺副刚度kT对该空间柔顺机构稳定性的影响，确定其作为关键参数对机构稳定性进行研究。

3）本文提出以带时标连杆特征点三维空间轨迹构造时变特征点位移序列动力学系统，引用动力学系统Lyapunov 指数作为稳定性指标研究机构运动稳定性，用Wolf 数值法求解计算最大Lyapunov指数。

4） 将最大Lyapunov 指数作为机构动力学系统稳定性的评价指标，以衡量空间柔顺机构运动稳定性；定量分析了不同柔顺副刚度kT下，多模式空间柔顺机构运动的稳定性，并从中分析出较优取值，保证其锁内应用稳定性。