冗余度双臂机器人协作策略下实时避障算法
李铁军,刘力源,刘今越,贾晓辉,武毅
(河北工业大学 机械工程学院,天津 300401)
相对于非冗余度机器人而言,冗余度双臂机器 人有良好的容错性、更好的灵巧性、更广的适用性等特性[1-2]。冗余度机械臂独有的自运动特点,使冗余度双臂机器人末端执行器执行协作任务的同时进行运动学及动力学二次优化[3]。随着智能机器人越来越多地用于执行复杂任务,因此机器人作业的安全性问题是无法回避的。考虑机器人作业过程中与作业环境避免发生碰撞,以及机器人双臂协调作业时避免双臂互相碰撞问题变得尤为重要[4-5]。
局部、全局路径规划通常是冗余度机械臂避障研究的两个方向[6]。对于实时避障而言,局部路径规划比全局路径规划的优势之处在于:其算法运算量小,使用一些视觉传感器实时获取作业环境中障碍物的位置信息,进而实现避障目标[7]。就目前看,国内外学者研究冗余度机器人避障方法时大都是以单臂机器人为研究对象[8-12],冗余度双臂机器人协调作业时避障研究仅考虑双臂自避碰[13-14]或机器人与环境障碍物的避障问题[15],同时考虑上述两种情况的研究相对少。
因此,本文提出一种协作任务下基于冗余度机械臂自运动特点的冗余度双臂机器人实时避障算法。首先对机器人做实时避障规划中,需要尽快的完成障碍物与机器人及机器人双臂之间的位置关系,且判断出易出现碰撞的杆件,从而完成避障动作。故提出一种预筛选投影矢量,说明其建立过程,然后根据机器人协作任务下双臂躲避障碍物的运动学逆解;再引入梯度“安全距离”指标估算机器人双臂之间、机械臂与环境障碍物之间碰撞程度,由此调整机械臂避障标志点的速度,保证机器人避障动作的连续性和平滑性。实现冗余度双臂机器人完成协作任务的同时机器人双臂相互之间不碰撞及机器人躲避作业环境中的障碍物任务。
1 预筛选投影矢量参数指标的建立
1.1 预筛选投影矢量参数
作为传统的避障指标Hmin可以很好地衡量障碍物距离机械臂的危险程度[8]。该指标主要是先计算障碍物与机械臂的各个连杆标志点的距离,再选择出对应距离最小的机械臂连杆,该杆件即为避障杆件。冗余度双臂机器人在做避障路径规划的场景下,使用Hmin的方法求取避障杆件,需要遍历所有的机械臂连杆的杆件,比较机器人双臂连杆之间及双臂连杆与障碍物之间的最短距离,消耗了大量的时间。
针对上述指标的不足,本文提出了预筛选投影矢量参数指标的方法:首先采用胶囊体包络法简化机械臂,对障碍物采用球形包络。在计算障碍物与机械臂连杆间最短距离之前,先根据障碍物在机械臂杆件上的投影位置情况,粗筛选掉一些不会碰撞的杆件,再去计算可能发生碰撞的杆件与障碍物最短距离,减少掉一些不必要的运算量。
1.2 预筛选投影矢量参数评估
以平面三自由度机械臂为例,假设障碍物与机械臂的一般位置关系如图1 所示,图中红色虚线部分为机械臂的胶囊体包络体,其包络半径设为R, 蓝色部分为障碍物的球形包络体,其包络半径设为Ro。
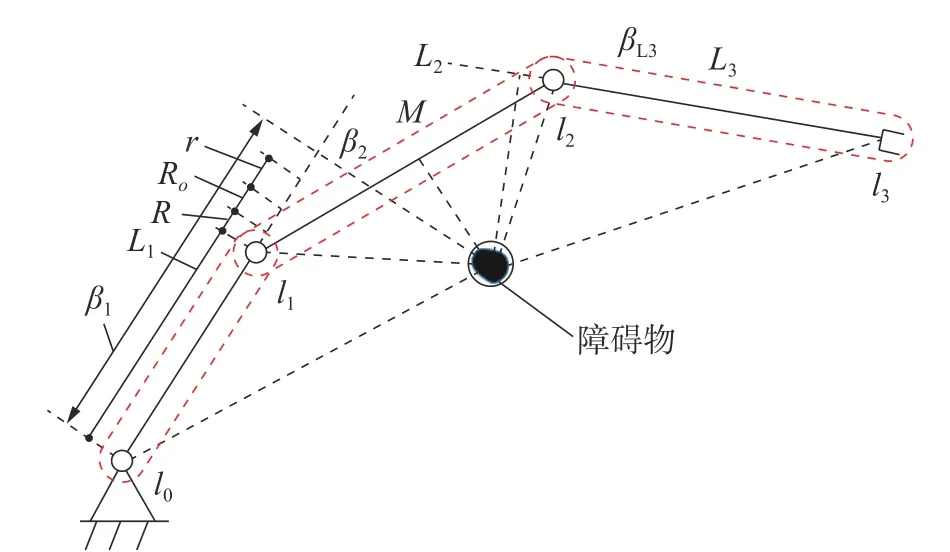
图1 冗余度机器人碰撞模型Fig.1 Collision model of a redundant robot
设机械臂的第i杆件关节端点li、li-1的位置矢量分别为m,n,Li为对应的机械臂杆件长度,机械臂的第i杆件在基坐标系{OB}下可表示为
在基坐标系{OB}下障碍物中心在机械臂的第i杆件上的投影矢量βi为
式中c为基坐标系{OB}下障碍物包络中心位置。
障碍物在机械臂杆件上的投影位置情况可分为以下3 种情况:
1)当βi>(Li+R+Ro+r)时,r为设定的距离阈值。机械臂的第i杆件为非避碰杆件,在下一步计算障碍物到机械臂的各个杆件最短距离时忽略该杆件;如图1 中机械臂第一个连杆与障碍物的位置关系。
2)当βi< -(R+Ro+r)时,机械臂的第i杆件为非避碰杆件,在下一步计算障碍物到机械臂的各个杆件最短距离时忽略该杆件;
3)当(Li+R+Ro+r)≥βi≥-(R+Ro+r),机械臂的第i杆件为可能避碰杆件,为了进一步确认避碰情况需要计算障碍物到该杆件距离去判断,如图1中机械臂第二、三个连杆与障碍物的位置关系。
通过上述分析,冗余双臂机器人杆件数量多,在计算障碍物和机器人各个杆件距离之前,先进行预筛选,剔除安全杆件,即不发生碰撞的杆件,只考虑可能与障碍物发生碰撞的杆件,减少不必要的计算量。
1.3 机械臂与障碍物最短距离解算
假定机械臂的第i杆件在进行1.2 节的预筛选检测之后,判定为不安全杆件,为了进一步判断该杆件与障碍物碰撞的危险程度,需要计算该杆件与障碍物之间的距离,进一步分析。
在基坐标系{OB}下机械臂的第i杆件距离障碍物最近位置标志点矢量Mi为

把障碍物和机器人机械臂体积大小考虑在内,则障碍物距离机械臂的第i杆件最短距离表达式为
计算所有非安全杆件上标志点与障碍物的距离,通过比较各距离值的大小,找到最短距离。
2 冗余度双臂机器人避障运动空间
在空间机器人双臂协作过程中,机械臂的运动是三维空间运动,机械臂躲避障碍物时,机械臂对应的标志点避障运动方向为沿着障碍物中心指向标志点的直线方向,机械臂避障缩减为一维空间运动[5]。减少避障算法的计算量,提高计算效率。
以机器人主臂为例,机器人的从臂为主臂的障碍物,在求解主臂避障标志点的避障方向时,先把主的各个杆件用式(1)~式(5)求解,得到主臂的各连杆与障碍物(包括环境障碍物与从臂)的距离,通过比较各个距离的大小,求解出最短距离d0L对应机械臂杆件上的标志点M0L的位置记作x0L,如图2 所示。
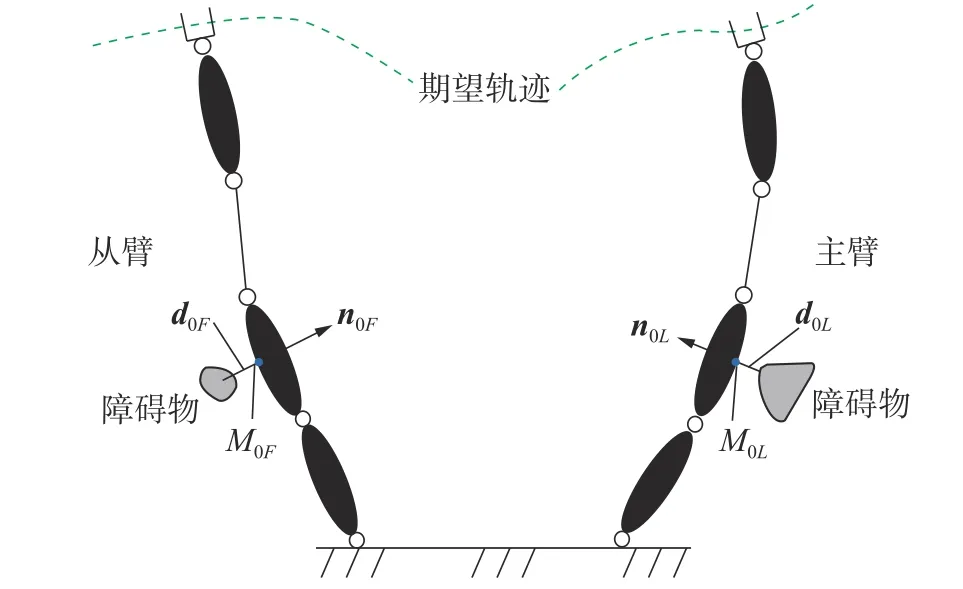
图2 冗余度双臂机器人避障运动示意图Fig.2 Schematic diagram of obstacle avoidance motion for redundant dual arm robots
机器人主臂上标志点避障方向为
则缩减避障运动空间后,主臂上标志点速度ẋd0L及雅克比矩阵Jd0L分别为:
同理,缩减避障运动空间后,从臂上标志点速度ẋd0F及雅克比矩阵Jd0F分别为:
3 冗余度双臂机器人协作运动学约束方程
冗余度双臂机器人执行搬运任务过程中,机器人双臂与被搬运物体之间会形成一条闭式运动链。这条闭式运动链需要满足一定的运动关系[16-17],方可实现机器人双臂的协作任务。
机器人双臂和刚体相互间的绝对运动学约束方程为
式中:ẋO为刚体中心绝对速度,ẋO∈R6×1;ṖO、ωO分别为在参考坐标系{OB}下的刚体中心绝对线速度、绝对角速度;JO为对应的雅克比矩阵,JO∈R6×14。
机器人双臂和刚体相互间的相对运动学约束方程为
式中:ẋr为刚体中心相对速度,ẋr∈R6×1;Jr为对应的雅克比矩阵,Jr∈R6×14。
结合式(11)和式(12),得到冗余自由度双臂机器人运动学表达式为

4 冗余度双臂机器人协作策略下实时避障算法
由式(8) ~ 式(14)及冗余度机器人速度级逆运动学方程的得到冗余度双臂机器人协作策略下的避障算法
为了高效地控制机器人双臂躲避障碍物保证其协作任务,故引入两个避障因子,式(14)可改为
式中:w1L、w1F分别为关节角速度因子;w2L、w2F分别为主、从臂上标志点避障速度因子。
引入梯度“安全距离”dn(n=1, 2, 3),确保机器人双臂避障过程中运动平滑性与连续性。其中w1L、w1F、w2L、w2F和dn之间的关系为:
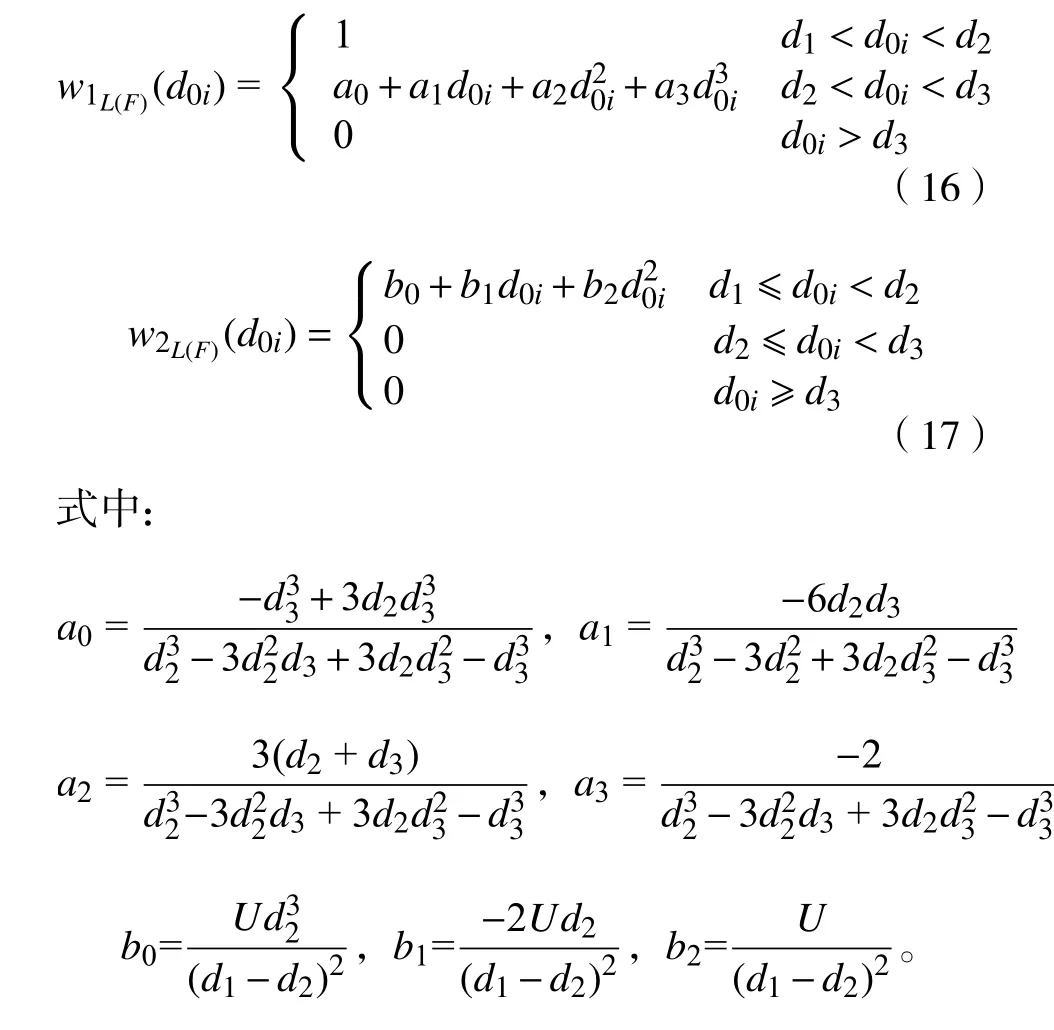
w1L、w1F、w2L、w2F和梯度“安全距离”dn的关系如图3 所示。
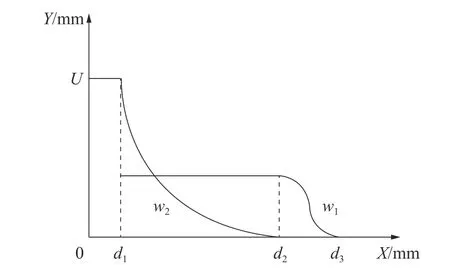
图3 w1、w2 与安全距离d 之间的关系Fig.3 The relationship between w1, w2 and safety distance d
由图3 可知,当机械臂上标志点与障碍物之间的距离d0i>d3时,为安全阶段,障碍物对机械臂的运动没有影响,机械臂不产生避障运动。式(15)可写为
当机械臂上标志点与障碍物之间的距离d2 当机械臂上标志点与障碍物之间的距离d1 以平面冗余自由度度双臂机器人为仿真实验对象,验证上述算法的可行性。如图4 所示,机器人的基坐标系为{OB},qi j、lij(i=L,F;j=1,2,3,4)分别为机器人双臂关节转角、机器人双臂各个杆件长度,其中关节转动的正方向记为“ + ”。 图4 平面冗余度双臂机器人Fig.4 Planar redundant two-arm robot 避障仿真实验在MATLAB R2019 软件下开始。设定机器人双臂杆件长度分别为:lL1=lF1= 240 mm,lL2=lF2= 260 mm,lL3=lF3= 200 mm,lL4=lF4= 65 mm;机器人双臂各个关节初始转角分别为:qL1= 60°,qL2=50°,qL3= -40°,qL4= -70°,qF1= 120°,qF2= -50°,qF3=40°,qF4=-70°。机器人包络半径均为10 mm,标志点的避障速度为10.8 mm/s,梯度安全距离分别为d1=12 mm,d2= 28 mm,d3= 45 mm。 机器人双臂协作任务是两机械臂的末端执行器一起夹持一个刚性物体,把刚性物体从起始位置(640,0) mm 沿直线搬运至终点位置(380,0) mm,协作空间内环境障碍物中心的位置分别为O1(230,-210) mm,O2(220,185) mm,障碍物的半径为 10 mm,整个仿真时长为10 s。 在未使用避障算法对冗余度平面双臂机器人进行避障路径规划的情况下,机器人双臂运动轨迹如图5 所示。该机器人双臂末端执行器能够很好地完成搬运物体的目标协作任务。但是在t= 5 s 时,机器人双臂的第一杆件末端发生了干涉;在t= 8.1 s时,机器人主臂的第二杆件同环境障碍物O1发生了碰撞干涉;在t= 8.5 s 时,从臂的第二杆件同环境障碍物O2发生了碰撞干涉,这也从侧边说明对机器人进行避障路径规划的重要性。 图5 未使用避障算法时机械臂的轨迹Fig.5 Trajectories of without-obstacle avoidance algorithm 当只考虑双臂自身的影响时,机器人双臂运动轨迹如图6 所示。机器人双臂末端执行器能够完成搬运物体的目标协作任务,同时机器人双臂可以相互避开。但在在t=9.3 s 时,机器人主臂的第二杆件同环境障碍物O1发生碰撞干涉,在t=9.4 s 时,从臂的第二杆件同环境障碍物O2发生碰撞干涉。 图6 只用自避障算法时机械臂的轨迹Fig.6 Trajectories of using only self-avoidance algorithm 机器人双臂协同作业时,同时考虑双臂互相干涉以及环境障碍物的干涉,使用本文提出的冗余度双臂机器人实时避障算法后,其双臂运动轨迹如图7 所示。此时机器人双臂与障碍物(包括环境障碍物以及双臂互为障碍物的情况)之间最短距离变化如图8 所示。双臂各个关节转角变化如图9 所示。 图7 使用环境障碍物避障与自避障算法机械臂的轨迹Fig.7 Trajectories of using only self-avoidance and environmental obstacle avoidance algorithm 图8 机器人双臂与障碍物之间的最短距离Fig.8 The shortest distance between robot's arms and obstacles 图9 机器人双臂关节转角变化Fig.9 Changes in the angle of rotation of robot arm joints 图8 和图9 表明:机器人双臂杆件间的最短距离以及双臂与环境中的障碍物之间的最短距离在t=0~2.8 s 内大于安全距离d3,双臂末端执行器执行协作任务,机械臂不执行避障任务;随着机器人双臂各关节的运动,在t= 2.8~6.5 s 内,机器人双臂的主臂与从臂的各连杆距离最短,双臂进入相互避障过程,机器人双臂各自的第一杆件末端距离逐渐缩短,该距离位于d2到d3区间内,为次安全阶段,双臂末端执行器执行协作任务,同时双臂执行避障任务;在t=6.5~10 s 时,机器人主臂第二杆件距离环境障碍物O1的距离小于主臂第一杆件距离从臂的各个杆件的最短距离,主臂开始躲避环境障碍物,随着主臂与障碍物O1之间的最短距离逐渐缩减,机械臂的避障动作变大;在t=6.5~10 s 时,从臂的第二杆件距离环境障碍物O2的距离小于从臂的第一杆件距离主臂各个杆件的最短距离,从臂开始躲避环境障碍物,随着从臂与障碍物O2之间的最近距离逐渐缩减,机械臂的避障动作变大。 仿真过程中,其双臂各杆件间最短距离及双臂与障碍物间最短距离始终大于梯度安全距离d2,由此可以看出使用本文避障算法后,不仅实现机器人双臂之间的相互避障,还实现双臂躲避环境障碍物,保证机器人在执行协作任务过程中的安全性。 根据图9 可以得出,机器人双臂在执行协作目标任务以及双臂躲避障碍物的过程中,机械臂的各个关节转角不发生突变。因此,使用本文提出的避障算法,冗余度平面双臂机器人顺利平稳地完成目标协作任务及避障任务。 为了进一步验证文中算法的实践应用效果,以MOTOMAN-SDA10 冗余度空间双臂机器人为实验对象,它由两个七自由度的串联机械臂组成,其左臂为从臂(Follow),右臂为主臂(Leader),主、从机械臂为对称式结构,机械臂相邻关节的旋转轴垂直。其结构简图如图10 所示,所搭建的平台如图11 所示。 图10 机器人结构简图Fig.10 Schematic diagram of robot structure 图11 实验平台搭建Fig.11 Establishment of an experimental platform 实验时,图漾相机获取环境障碍物的位置,把障碍物的位置转换到机器人基坐标系下,再把障碍物的位置及机器人末端期望速度信息输入到避障算法中,得到避障后的机器人的关节角数据,最后把关节角的数据转为关节角脉冲发送到机器人控制柜,驱动关节伺服电机,机器人到达指定位置。 机器人双臂的胶囊体包络半径设为150 mm,机械臂各关节初始转角分别设置为:qL1= 20°,qL2=20°,qL3= 0°,qL4= 120°,qL5= 0°,qL6= -20°,qL7=0°,qF1= 20°,qF2= 160°,qF3= 0°,qF4= 120°,qF5=0°,qF6= 20°,qF7= 0°。避障碍物的速度为15.6 mm/s,梯度“安全距离”分别为:d1= 10 mm,d2= 45 mm,d3=75 mm。被搬运物体中心的初始、终止位置分别为:(569.2,0,207.2) mm,(919.2,0,-142.8) mm。 冗余度机器人双臂协调操作的任务为:双臂协作搬运刚性工件,工件长度为500 mm,将其从初始位置匀速沿直线搬运到末端位置,给定两个半径r=30 mm 的球形障碍物,球中心位置分别为:O1=(500, -488, -8) mm,O2= (475, 545, -7) mm。冗余度双臂机器人协作运动过程如图12 所示,双臂协作过程中,机器人双臂与障碍物(包括环境障碍物以及双臂互为障碍物的情况)之间最短距离变化如图13 所示,此过程中机器人双臂各个关节转角变化如图14 所示。 图12 考虑机器人本体互为障碍和环境障碍物的影响下机器人协作运动情况Fig.12 The cooperative motion of a robot is considered when the influence of the arms are mutual obstacles and environmental obstacles 图13 机器人双臂与障碍物之间的最短距离Fig.13 The shortest distance between the two arms of the robot and obstacles 由图12~图14 可知:采用本文算法进行避障规划,各关节运动连续、平稳,且可保证双臂各连杆之间、双臂各连杆与环境障碍物之间的最近距离始终大于设定的阈值d2。保证机器人双臂协作过程中的安全,且双臂能够完成协作任务。 针对冗余度双臂机器人操作环境的复杂性,提出了机器人实时自身避障及躲避环境障碍物的协作路径规划算法。通过预筛选投影矢量指标,筛选掉机械臂中不会碰撞的杆件,减少计算量,再实时计算可能发生碰撞的杆件与其余机械臂杆件及环境障碍物之间的最短距离,并与设定的梯度“安全距离”比较,评估障碍物与机械臂碰撞的危险程度,并实时改变机械臂上标志点的避障速度,最后通过仿真及实验验证了该算法的可行性,确保机器人双臂执行协作作业过程的安全。5 仿真分析
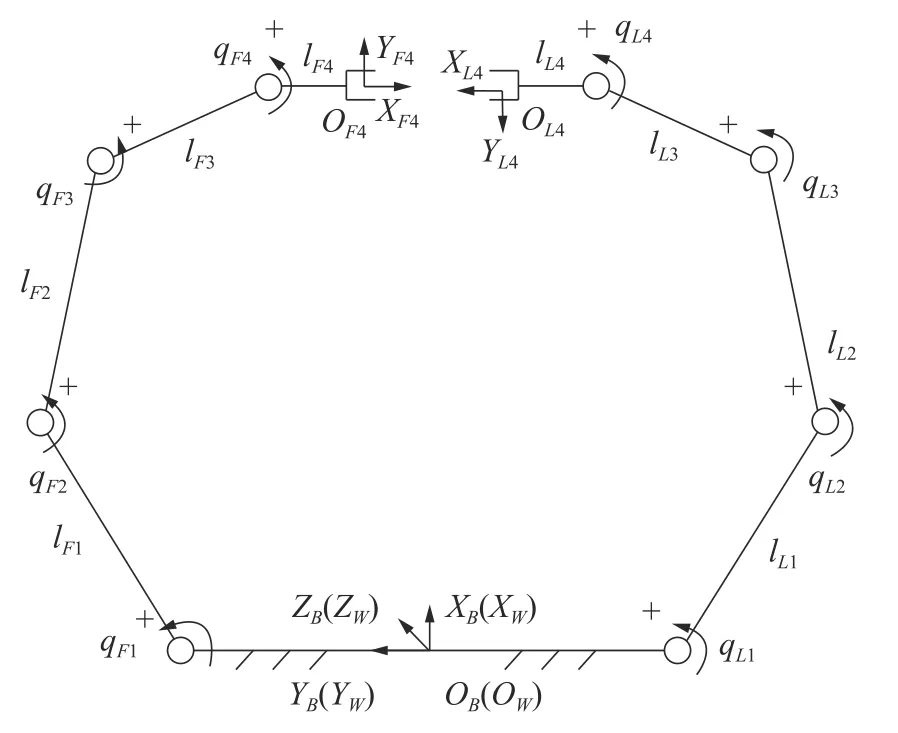
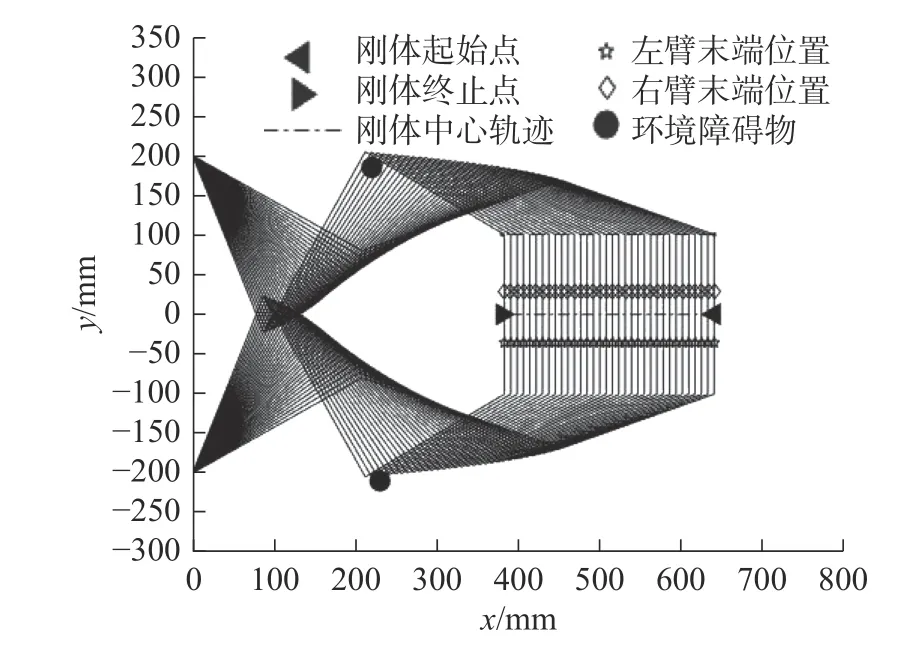
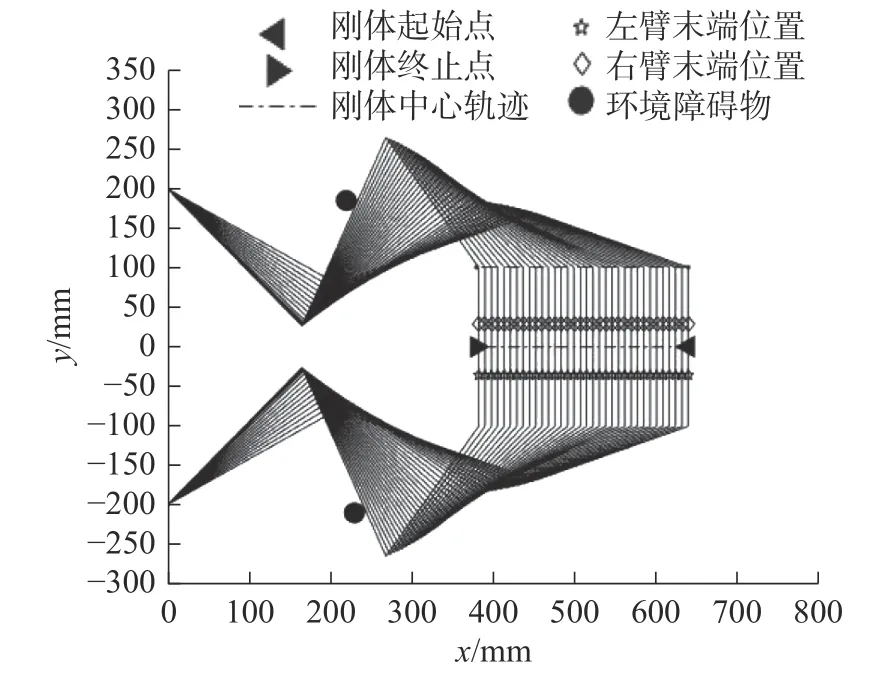

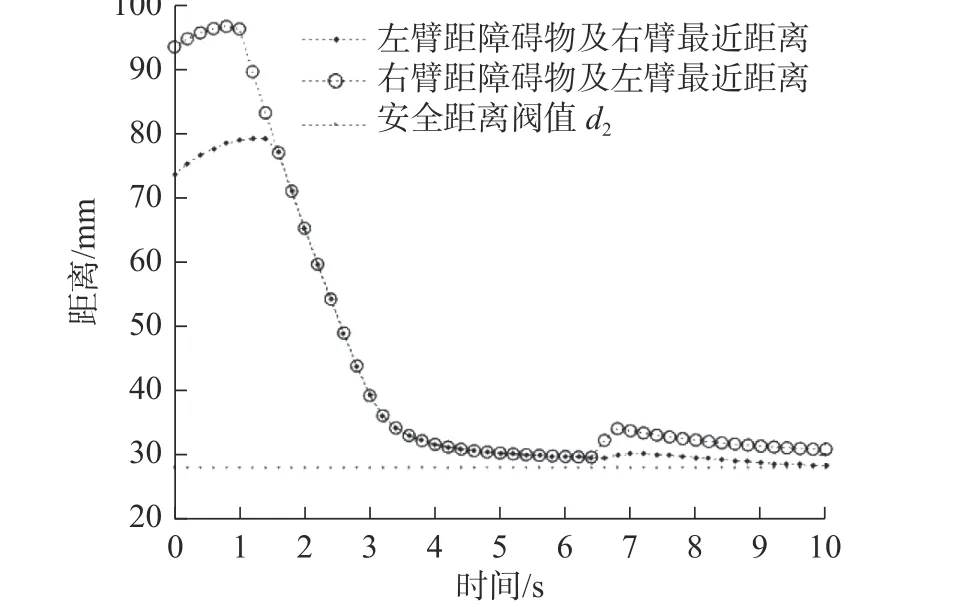
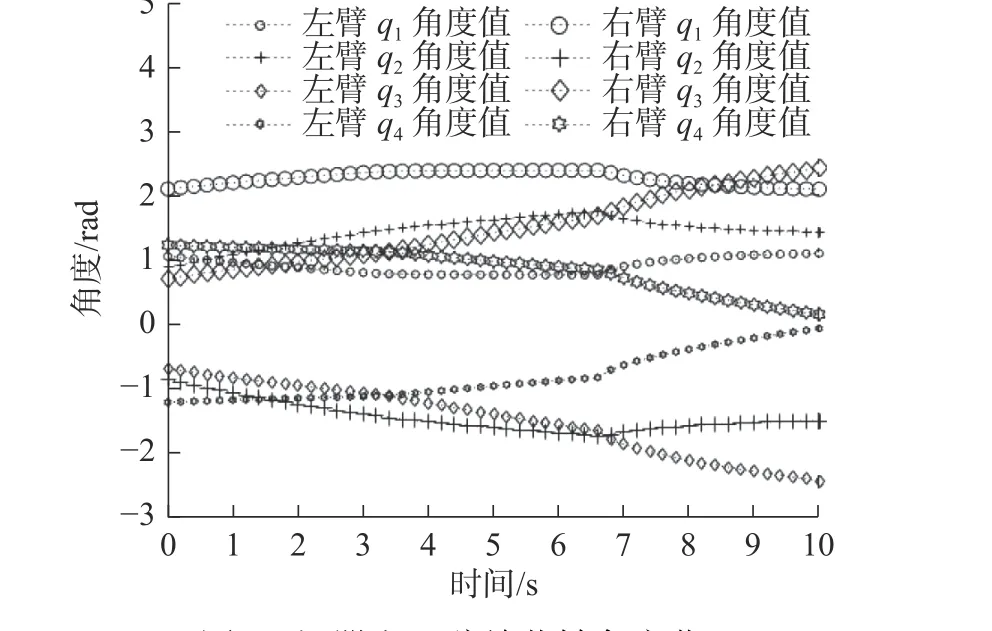
6 实验验证


7 结论

