高低阀串联型特高压柔性直流不控整流异步充电时分压特性及其对系统的影响

刘汉军，周竞宇，盛俊毅，任成林，胡雨龙

（1.特变电工西安柔性输配电有限公司，西安 710000；2.中国南方电网超高压输电公司，广州 510620）

0 引言

高低阀串联型特高压混合多端柔性直流输电系统在远距离大容量输电方面具有优势［1-5］，可实现多电源供电和多落点受电，近几年得到越来越多的关注和研究［6-10］。特高压混合多端直流输电系统结合了LCC-HVDC（line-commutated converter based high voltage direct current）与VSC-HVDC（voltage source converter based high voltage direct current）的优势［11-14］，与传统直流输电系统相比，无换相失败问题并且可以向弱受端交流电网供电，实现海上风电场的功率输送［15-17］；与多端柔性直流输电系统相比，功率损耗较小且降低了换流器与电缆投资成本［18-19］，具有良好的发展前景。

目前国内针对多端混合直流输电系统展开了一系列研究，文献［20］对系统的启动和停止等关键控制策略以及一端投退对多端混合直流输电网络的影响进行了实验研究。文献［21］针对同一换流站内串联换流阀组之间的电压不平衡问题，分析了电压不平衡的原因，并提出了一种基于串联换流阀组间电压-功率偏差量的电压平衡控制策略。文献［22］基于特高压混合多端直流输电系统对线路故障处理的需求，分析了该系统直流线路保护的关键问题，并提出了直流线路保护配置方案和直流线路保护的配合策略。文献［23］针对三端柔性直流输电系统正常启动，设计了“一拖二拟合启动”的方式，即由一个逆变站带两个整流站启动，启动过程中适时切换控制方式，以获得平稳的启动过程。文献［24］讨论了柔直系统的启动策略以及子模块充电过程中出现的电压发散问题，从日常运维角度提出合适的改进措施。文献［25］分析了柔性直流换流站启动过程中对交流电网电压产生严重影响的各种因素。

以上文献均未提到特高压混合直流输电系统异步充电时阀组分压的问题，以及阀组异步充电对系统的影响。本文以特高压多端混合直流输电系统为研究对象，对换流器及直流输电线路进行等效，研究不同运行方式下系统的充电回路，分析阀组异步充电的分压特性及阀组分压对系统的影响。

1 理论分析

图1 为特高压混合三端直流输电系统，整流站为LCC（line-commutated converter）、2 个逆变站均为MMC（modular multilevel converter），该系统采用真双极结构，送端LCC换流站正、负极均采用双十二脉动换流器；为了满足特高压的需求，2 个逆变站的正、负极均采用2 个MMC 换流器高低阀组直接串联的形式。

图1 特高压混合三端直流输电系统示意图Fig.1 Schematic diagram of UHV hybrid three terminal DC transmission system

对于含全桥模块的多端混合柔性直流输电系统，当换流站多个阀组交流充电不同步时，在特定连接形式下交流断路器未合闸的阀组与交流短路器合闸的阀组形成充电回路，给交流断路器未合闸的阀组的全桥模块充电，即感应电压充电，严重时可引起阀组过压、半桥模块充不上电等问题，从而造成系统保护跳闸，因此有必要对换流阀分压特性进行分析，提出感应电压抑制策略，解决感应电压充电问题。本节将从换流器等效模型、线路等效模型、充电回路等几个方面分析阀组分压特性。

1.1 换流器等效模型

对于高低阀结构的柔性直流输电系统，以低阀交流断路器合闸、高阀交流断路器分闸为例，充电回路如图2 所示。低阀通过交流电源给阀组充电，充电电流只在本阀组内部流动；高阀通过感应电压充电，充电电流为负，全桥模块充电，6 个桥臂电流大小和方向相同，充电电流汇集后经输电线路返回另一个阀组，形成电流通路。

图2 低阀交流充电与高阀感应充电回路Fig.2 Low valve AC charging and high valve induction charging circuit

低阀交流充电模式下，低阀直流电压被交流电压钳位，可等效为电压源，其电压UV1大小约为：

式中Uvalve为换流变压器阀侧线电压有效值。

高阀被动充电可等效为RC 并联回路，电阻包含均压电阻Red和模块取能电源等效电阻Rps，电容和电阻均由上下桥臂全桥模块串联再三相并联组成，高阀的等效电阻Rv、等效电容Cv为：

式中：NsmF为全桥模块数；Csm为模块电容。当功率模块电压足够高后，取能电源开始工作，取能电源可近似等效为恒功率负载，其等效电阻阻值随模块电压变化，其等效电阻可用式（3）近似计算。

式中：Usm为功率模块电压；Pps为取能电源损耗。

1.2 直流线路等效模型

直流线路模型如图3 所示，直流线路可等分成n段，每段线路包含极对地、极间的分布参数。分析直流特征时，可忽略线路电感li、线路互感lm的影响，由于线路电阻ri远小于对地电阻，分析时忽略线路电阻。

图3 直流线路模型Fig.3 DC line model

直流线路模型等效模型如图4 所示，直流线路参数简化见式（4）。

图4 直流线路等效模型Fig.4 Equivalent model of DC line

式中：Cgi、Rgi分别为第i段线路对地电容和对地电阻；Cmi、Rmi分别为第i段路线间电容和线间电阻；Cg、Rg分别为线路对地总电容和对地总电阻；Cm、Rm分别为线间总电容和线间总电阻。

电容充电达稳态后，各部分电压由电阻分压决定，充电回路忽略换流阀等效电容Cv、线路间电容Cg与线路对地电容Cm的影响。根据测算，极线间电阻Rm=5.8 MΩ，极线对地电阻Rg=2.52 MΩ。

1.3 充电回路分析

在单极大地回线运行方式下，得到极2 低阀带电后充电分析模型及简化电路模型如图5 所示，图中Cdc为另一端直流滤波电容。极2 单极大地回线运行时，极1 悬空，两端换流站通过大地构成回路，极1 电压不为0。极2 带电工作后，极1 存在电压，线路间电阻Rm与线路对地电阻Rg之间的比值关系见式（5）。

图5 单极大地回线下极2低阀带电后充电分析模型及简化电路模型Fig.5 Monopole earth loop charging analysis model and simplified circuit model of pole 2 low valve charged

式中：UP1为极1 电压；UP2为极2 电压。单极大地回线下的分压关系见式（6）。

式中：U2lv为极2 低阀直流端口电压，取344 kV；U2hv为极2 高阀直流端口电压；R2hv为极2 高阀等效电阻，当全桥模块电压为284V时，R2hv=0.491 MΩ，单极大地回线运行方式下R2hv∶Rg∶Rm≈1∶3.27∶7.53，Rg取1.6 MΩ，Rm取3.7 MΩ，代入式（6）得U2hv为98 kV。

在单极金属回线运行方式下，得到极2 低阀带电后充电分析模型及简化电路模型如图6 所示。单极金属回线运行时，接地点在另一端换流站站内，极1 的Cg、Rg回路经旁路刀闸短接被短路、极1 电压为0，则单极金属回线下的分压关系见式（7）。

图6 单极金属回线下极2低阀带电后充电分析模型及简化电路模型Fig.6 Monopole metal loop charging analysis model and simplified circuit model of pole 2 low valve charged

式中：当全桥模块电压为284 V 时，R2hv为0.7 MΩ，单极金属回线运行方式下R2hv∶Rg∶Rm≈1∶2.6∶6，Rg取1.8 MΩ，Rm取4.2 MΩ；U2lv为344 kV；代入式（7）得U2hv为122.2 kV。

在双极三阀组金属回线运行方式下，极2 高低阀充电完成、极1 未充电时的充电回路模型如图7所示，极1电压不为0，则极1分压关系见式（8）。

图7 双极三阀组充电回路模型Fig.7 Charging circuit model of bipolar three-valve group

式中：U1lv为极1 低阀直流端口电压；R1lv为极1 低阀等效电阻，当全桥模块充电至300 V 时，R1lv为0.75 MΩ。Rg取2.52 MΩ，Rm取5.8 MΩ，U2lv和U2hv均取344 kV，代入式（8）计算得U1lv为62.3 kV。

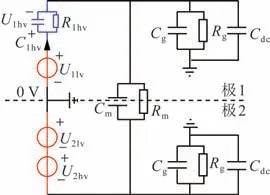
图8 双极四阀组充电回路模型Fig.8 Charging circuit model of bipolar four-valve group

式中：U1hv为极1 高阀直流端口电压；R1hv为极1 高阀等效电阻；UP2为极2电压（等于U2lv与U2hv之和）。当全桥模块充电至1 200 V 时，R1hv为3.0 MΩ，Rg取2.52 MΩ，Rm取5.8 MΩ，U1lv取344 kV，UP2取688 kV，代入式（9）计算得U2hv为348.4 kV。

对于不带线路运行方式（open line test，OLT），极2低阀充电后、高阀充电前，由于直流线路未连接，极线对地电阻R极大，高阀直流端间电压较低，此时分压回路如图9 所示，极2 高阀分压为：

图9 不带线路OLT运行低阀充电后高阀充电前分压回路Fig.9 OLT operation partial voltage circuit of low valve charged and high valve uncharged

感应充电阀组只有全桥模块充电，全桥模块平均电压Vsub为：

式中Uv为交流断路器未合闸阀组直流电压，当直流电压Uv为19.2 kV 时，计算得全桥模块电压约61.5 V。

2 仿真分析

以乌东德特高压多端混合柔性直流输电工程为例，该工程为真双极高低阀串联结构的混合直流输电系统，昆北站为±800 kV 8 GW 的LCC 换流站，龙门站为±800 kV 5 GW 的MMC 换流站，柳北站为±800 kV 3 GW 的MMC 换流站。MMC 换流站主要电气参数如表1所示。

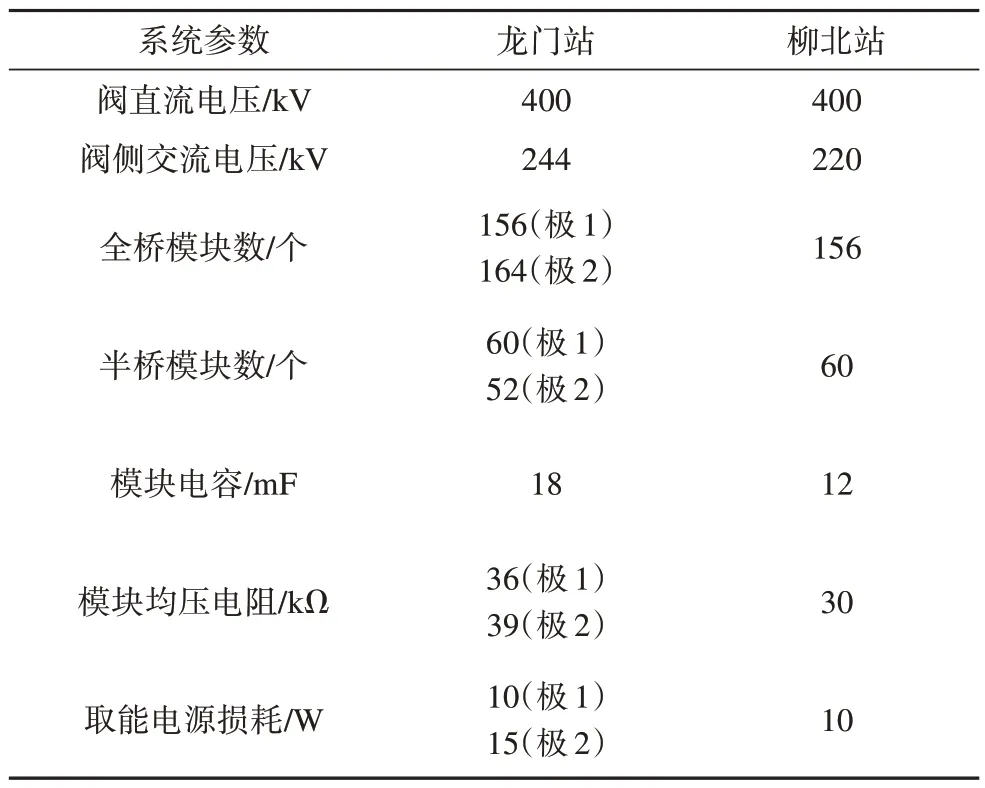
表1 MMC换流站主要电气参数Tab.1 Main electrical parameters of MMC station

2.1 单极大地回线运行方式

根据现场试验结果，单极大地回线运行方式下，极2 带电工作后，极1 存在电压，其电压约为极2 电压的30%，由式（5）可推算线路间电阻Rm与线路对地电阻Rg之间的比值关系为Rm≈2.3Rg。

单极大地运行方式试验中，龙门极2 高阀交流断路器未合闸，直流电压为-98.5 kV，联立式（5）-（6）可 得Rv∶Rg∶Rm≈1∶3.27∶7.53，代入仿真模型得到的仿真结果如图10 所示，高阀直流端口电压为-92.3 kV，全桥模块平均电压为284 V。

活动的频度是课余足球活动得以存在和发展的最基本的时间因素，反映了大学生在正常学习时间外，每周参加足球活动的次数。从调查中可以看出，有35%的学生参与活动次数在1-2次之间，40%的学生参与活动次数在2-3次。20%的学生在3-4次左右。可以看出，大部分足球爱好者每周活动频率在4次以内，符合高职院校学生对足球运动的需求。

图10 龙门极2单极大地回线运行方式仿真波形Fig.10 Simulation wave of monopole earth loop Longmen pole 2

2.2 单极金属回线运行方式

单极金属回线龙门站直流侧（Rm与Rg并联）等效电阻比单极大地回线下等效电阻更大（Rm+Rg后与Rg并联），因此单极金属回线下直流极线电压更低（金属回线下222 kV、大地回线下245 kV）。此过程中功率模块取能电源不断开始工作，高阀等效电阻Rv不断变化；同时RC回路不断放电，放电时间常数达到数分钟级。在低阀带电到高阀带电的十多分钟时间内，无法准确找到“稳态”，以下推算结果只用于预测相关数值的数量级，无法准确评估数值大小。

单极金属回线运行方式试验中，龙门极2高阀交流断路器未合闸，直流电压为-121.7 kV，联立式（5）、式（7）可得Rv∶Rg∶Rm≈1∶2.6∶6，代入仿真模型得到的仿真结果如图11所示，高阀直流端口电压为-114.9 kV，全桥模块平均电压为350 V。

图11 龙门极2单极金属回线运行方式仿真波形Fig.11 Simulation wave of monopole mental loop Longmen pole 2

2.3 双极三阀组运行方式

昆龙三阀组试验，龙门极2 充电完成、极1 尚未充电，试验过程该状态维持约5 min，极1直流电压升高至-56 kV。

在当前回路下，若模块充电至300 V、取能电源正常工作时，由式（2）可得高阀等效电阻Rv约为0.75 MΩ。

双极四阀组试验中求得极线间电阻Rm=5.8 MΩ，极线对地电阻Rg=2.52 MΩ，代入仿真模型得到的仿真结果如图12所示，极1阀交流断路器未合闸，直流端口电压为-57.7 kV，全桥模块平均电压为187 V，小于300 V，表明全桥模块无法被充电至稳定取能。

图12 龙门双极三阀组运行方式仿真波形Fig.12 Simulation wave of Longmen bipolar three valve group

2.4 双极四阀组运行方式

开展昆龙四阀组试验时，龙门极2、极1 低端充电完成、极1 高端未充电，试验过程该状态维持约5 min，极1 直流电压降低至-10 kV，极1 高端换流阀端间电压最高达到-350 kV且还在继续升高中。仿真结果如图13所示。

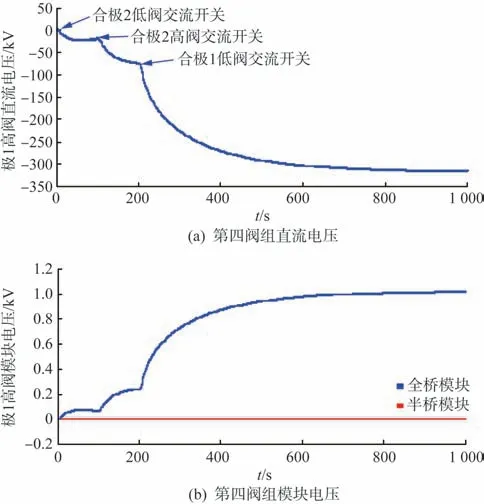
图13 龙门双极四阀组运行方式仿真波形Fig.13 Simulation wave of Longmen bipolar four-valve group

功率模块电压约为1 200～1 370 V，取能电源等效电阻为144～188 kΩ。龙门极1 模块均压电阻为36 kΩ，IGBT 无开关动作时取能电源损耗约为10 W，考虑损耗电阻后为28.8～30.2 kΩ，每桥臂模块数量为156个，则此时Rv为3～3.14 MΩ。结合Rm=2.3Rg，解方程可得Rm=5.8 MΩ，Rg=2.52 MΩ，代入仿真模型得到的仿真结果如图13所示，极1阀高阀交流断路器未合闸，直流端口电压为-316 kV，全桥模块平均电压为1 013 V，大于300 V，表明全桥模块能被充电至稳定取能。

2.5 不带线路OLT式

柳北站极2 不带线路OLT 试验时仿真波形如图14 所示。低阀充电后、高阀充电前，极2 高阀交流断路器未合闸，直流端口电压约-19.2 kV，全桥模块平均电压为62 V，小于300 V，表明全桥模块无法被充电至稳定取能。

图14 柳北极2 OLT运行方式仿真波形Fig.14 OLT operation simulation wave of Liubei pole 2

3 试验结果

针对昆龙单极大地回线运行方式（图15 示例）、昆龙单极金属回线运行方式、昆龙三阀组运行方式、昆龙四阀组运行方式、柳北站不带线路OLT运行方式5 种情况，理论、仿真及试验统计数据如表2所示。

表2 阀组分压统计表Tab.2 Statistical table of valve group partial voltage

图15 单极大地回线运行方式录屏Fig.15 Recording screen of monopole earth loop Longmen pole 2

从表2 可知，理论计算、仿真数据和试验数据比较接近，验证了充电回路分析的正确性。

4 阀组分压应对策略

上述5 种充电试验中，四阀组运行试验最为恶劣，感应电压达到-350 kV，全桥模块平均电压可充至1 122 V，此时第四阀组进行交流充电，半桥模块电压理论还能充至782 V，取能电源还能可靠带电。但在一极解锁，另一极充电情况下，交流断路器未合闸的阀组的直流电压会更高，全当全桥模块充电至1 724 V 时，R1hv为3.0 MΩ，Rg取2.52 MΩ，Rm取2.77 MΩ，U1hv取344 kV，UP2取800 kV，代入式（9）计算得U2hv为519.7 kV。搭建图8所示仿真模型，得到极1 高阀端间电压和全桥模块电压如图16所示，极1高阀直流电压为-514.6 kV，全桥模块平均电压为1 650 V。

图16 龙门极2解锁极1充电仿真波形Fig.16 Simulation wave of Longmen pole 2 deblock and pole 1 charge

龙门极2 解锁极1 充电试验波形如图17 所示，试验中出现龙门极1高阀感应电压-518.5 kV，模块平均电压1 245 V，因感应电压下半桥模块不充电，则换算成全桥模块的平均电压为1 724 V，此时高阀再进行交流充电，半桥模块平均电压可充至352 V，考虑充电过程中模块电压存在分散性，会出现大量半桥模块带不上电，从而引起系统保护跳闸。

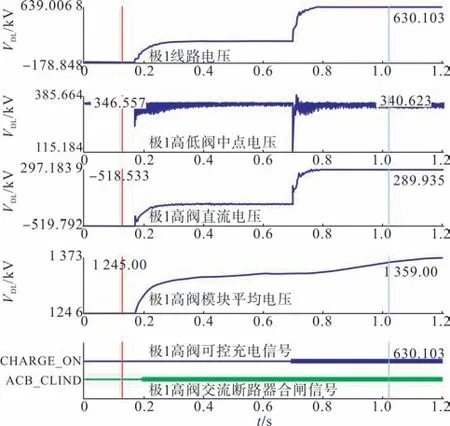
图17 龙门极2解锁极1充电试验波形Fig.17 Test wave of Longmen pole 2 deblock and pole 1 charge

针对上述阀组分压问题，结合系统结构形式提出以下应对策略。

1）对于所有类别充电，如单极大地回线充电、单极金属回线充电、带线路OLT 充电、不带线路OLT 充电、双极三阀组充电等，交流断路器未合闸阀组的直流电压不高，但由于充电时全桥模块电压存在分散性，感应充电时间较长亦可使一部分全桥模块取能电源带电，取能电源带电后阻抗特性发生变化，全桥模块取能电源可能频繁带电掉电，容易引起模块故障，因此可尽量缩短阀组间交流充电的时间间隔，从感应充电速度考虑，建议控制在10s以内。

图18 为极充电时序图，图19 为极充电现场试验波形，其中蓝色虚线为极1 低阀充电时刻，红色虚线为极1 高阀充电时刻，二者时间差约9 s，极1高端阀组直流端间电压充电至约40 kV，没有模块可靠取电，有效避免了感应充电过程。

图18 极充电时序图Fig.18 Pole charging sequence diagram

图19 极充电现场试验波形Fig.19 Field test waveform of pole charging

2）对于双极四阀组充电，若四阀组间交流充电时间间隔小于10 s，也可采用全交流充电模式；若长时间感应充电，因长时间充电感应充电电压较高，极端情况可能造成感应充电阀组直流电压过压、半桥模块无法带电的问题，应对此种情况可将第四阀组直流短接，其他3 个阀组交流充电过程中，第四阀组直流端口无感应电压，待其他3 个阀组交流充电完成后，第四阀组进行直流短接充电，然后在线投入第四阀组。

5 结论

特高压柔性直流系统交流充电阀组带电后，将通过线路杂散参数对交流断路器未合闸阀组的全桥模块充电，充电具有以下特点。

1）单极大地回线、单极金属回线运行方式下，交流断路器未合闸阀组直流电压可达100 kV量级；

2）通过实验结果与充电回路分析，线间电阻与线对地电阻对阀组分压影响较大，直流线路间电阻约为单回线对地电阻的2.3倍；

3）不带线路OLT 运行方式下，由于没有直流线路，正负极、极对地杂散电阻电容的阻抗、容抗远大于换流器，感应充电现象不明显，阀组分压低；

4）三阀组运行方式下，极2 充电后、极1 低阀全桥模块无法稳定取能，模块电压在取能电压门槛附近波动，由于稳定取能后才向录波系统上送模块电压信息，该状态下阀直流端间存在电压，录波中模块电压显示为0；

5）四阀组试验时，3 个阀组充电后，第四个阀组功率模块可以稳定取能，且该阀组等效电阻随着模块电压升高而增大，预计稳态时高阀直流端间电压可达370 kV 左右，高于模块从交流侧充电的端间电压。

针对阀组异步充电的分压问题，为保证阀组充电顺利进行，应尽量缩短阀组间交流充电的时间间隔，建议控制在10 s 以内；对于感应电压较高的四阀组充电，可将第四阀组直流短接充电，充电完成后在线投入。

本文通过几种主要充电模式，对充电回路进行了理论和仿真分析，分析结果与试验吻合，对于特高压柔性直流输电系统设计具有重要的参考指导意义。