基于Fluent-Direct Optimization耦合的木工刨床吸尘能力的理论分析

黄 勇

(四川省青城机械有限公司,四川 眉山 620460)

近年来,随着人们生活品质的提升,对实木家具的需求越来越大。木工刨床作为生产实木家具原料的设备越来越受到木材加工厂商的重视[1-2],特别是高质量的高速四面刨。而木工刨床吸尘能力的不足一直是困扰厂商的一个问题,木屑主要堆积在如下三个地方:

(1)工作台面上不仅影响台面上运动部件的灵敏度,还影响刨床的加工精度。

(2)由于吸尘能力不足,大量的木材切屑,如刨花,堆积在木工刨床的内部,这对设备内部零件的防尘和润滑设计是一个非常大的挑战,且设备内部有很多电气元件,堆积的切屑还会影响电气元件的散热。

(3)切屑堆积在刨床周围,不便清扫,影响工厂环境。漂浮在空气中的木材切屑粉尘对工人的职业健康造成很大影响[3-6]。

目前,国内、国际对木工刨床大多采用吸尘口从吸尘管道引出直接悬置于加工区域的上方进行吸尘[7],但吸尘效果都不理想,特别是国内、国际正在大力发展的高速四面刨,相比传统的四面刨会产生更多的切屑,如果不能妥善地解决吸尘问题将会很大程度上限制高速四面刨的发展。

本文论述了一种从理论上分析吸尘能力的办法,为木工刨床设计阶段通过优化结构设计以改善吸尘能力提供了指导方向。

1 切屑的研究与建模

1.1 切屑的研究

四川省青城机械有限公司的木工刨床作为市面上的常见机型,笔者随意选取了其12件切屑作为本文的研究样本,切屑形态如图1所示,切屑形态参数如表1所示。经过测量和比对,发现切屑有以下特点:

表1 切屑形态参数

图1 切屑形态

(1)切屑的厚度波动范围为0.10～0.18,其样本众数为0.16,中位数为0.16。

(2)切屑大小波动范围较大,如5号样本3 mm×6 mm,2号样本7 mm×12 mm。

(3)切屑形状不一,有较为平整的切屑如9号,轻微卷曲的切屑如6、11号,完全卷曲的如8号。

1.2 切屑的建模

依据上文提到的切屑的特点,笔者选取切屑中平均厚度0.15 mm、切屑大小8 mm×11 mm、出现频率最高的轻微卷曲形状对切屑进行建模,切屑模型如图2所示。木材材质采用常见的松木。

图2 切屑模型

其中切屑模型的体积V= 13.51 mm3,密度ρ=0.55 g/cm3,质量m=0.007 430 50 g,重量G=7.281 89E-05 N。

2 分析吸尘工况并建立流场模型

为了确保能顺利吸走木屑,本文选用了最恶劣的工况,即:

(1)吸尘管道竖直放置,即吸尘气流方向与重力反向。

(2)采用在木屑的侧面作为迎风面,此时在木材切屑上产生的作用力较小。

依据上述工况,建立流体域模型如图3所示。

图3 流体域模型

3 流场仿真

本文采用FLUENT对上述吸尘工况进行仿真。采用Direct Optimization进行定向求解。

3.1 数学模型的建立与网格的划分

流动可以分为层流,层流-湍流过渡态,湍流三种流动状态。雷诺数是用来确定流动是层流还是湍流的标准[8]。雷诺数计算公式:

ReL=ρUL/μ=1.225×3.2×0.1/0.000 01=39 200

(1)

式中:ρ——流动介质的密度

U——介质的流动速度,内流问题为通道内平均流速

L——特征长度,内流问题为通道直径

μ——流动介质的动力粘性系数

对于内流问题,当雷诺数>2 300,会形成湍流。因此本次吸尘问题的模拟属于湍流问题。对于湍流问题,有三个基本的计算方法。

(1)直接数值模拟(DNS)方法。DNS在直接求解三维非稳态的流动控制方程时会对计算机的计算性能提出非常高的要求,很难用于工业领域。

(2) 大涡模拟(LES)方法。LES方法比DNS经济,但对于大多数实际应用程序来说,所需的工作量和计算资源仍然太大。

(3) 雷诺平均N-S方程 (RANS)方法。RANS方法是目前主流的解决实际工程问题的方法。RANS方法是将满足动力学方程的瞬时运动分解为平均运动和脉动运动两部分,对脉动项的贡献通过雷诺应力项来体现,再根据各自经验、实验等方法对雷诺应力项做出假设,从而封闭湍流的平均雷诺方程而求解的方法。

基于RANS方法,有多个湍流模型可用,有些仅用于非常特定的应用常用,工业上最广泛使用的湍流模型是SST k-ω。如果收敛困难,可以尝试BSL k-ω,或者 Realizable k-ε湍流模型。如果只需要湍流的粗略估算,则可以使用标准的k-ε模型。因此本次吸尘问题的模拟采用SST k-ω湍流模型。

在近壁区域,解梯度非常大,但近壁区域的精确计算对模拟的成功至关重要。因此在划分网格时需要添加边界层,通常可以选择办法是:

(1)采用壁面函数。壁面函数是利用函数来模拟壁面距离与速度的关系。一般来说,如果仿真的重点是区域中部湍流,而不是对壁上的力更感兴趣,则采用这种方法。

(2)采用粘性子层。要求网格的第一层的Y+≈1,并且网格大小的增长率不超过1.2。这会显著增加网格数量。一般来说,如果仿真的重点是壁面上的力或传热 (气动阻力,涡轮机械叶片性能,传热),通常使用粘性子层的方法。

本文主要研究气流产生的作用力,因此选用粘性子层,划分网格时为木屑添加边界层。边界层的高度、层数等信息可以网络搜索Y+ calculator代入数据进行计算。

采用fluent meshing划分多面体网格,效果如图4。

图4 网格划分效果图

3.2 设置边界条件并求解

设置如下边界条件:

(1)入口压力为0 Pa,即为大气压;

(2)出口压力设置为输入参数。

出口平均流速和气流在木材切屑上产生的作用力F作为输出参数。为了更准确模拟出气体流速,选用满足理想气体状态方程的理想气体作为流体域内介质,其属性如表2所示。本文为求出出口压力(负压),使得当出口压力低于此值时,气流在木材切屑上产生的作用力F不小于木材重力G,此时可以顺利吸走木屑。此处借助Direct Optimization模块,设置收敛准则为F=G,变量为出口压力,求解方式为Adaptive Single-Objective。经过9次自动求解迭代,得到F=7.281 92E-05 N,与木屑自重G=7.281 89E-05 N近似相等。仿真数据如表3所示。

表2 理想气体属性

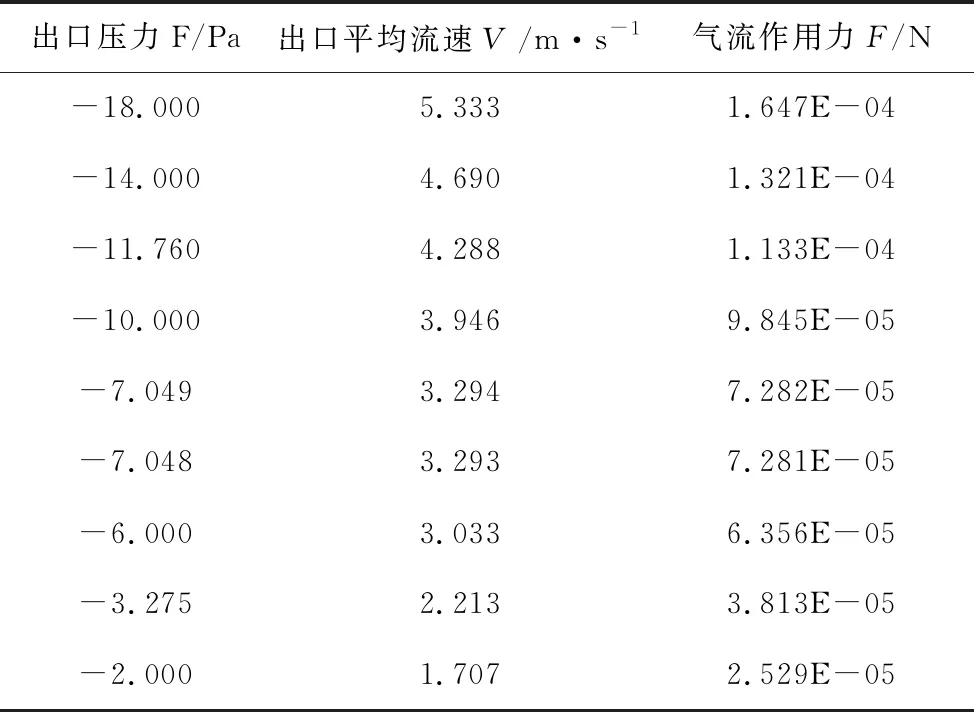
表3 仿真数据

3.3 仿真结果分析

由仿真结果可知,当出口负压为-7.049 Pa时,气流在木材切屑上产生的作用力F=7.281 87E-05 N,与木屑自重G=7.281 89E-05 N近似相等,此时流体域内的平均流速为V=3.294 m/s。木屑在流场中受力如图5所示。

图5 木屑受力情况

建立一个流体域的横截面,横截面需穿过木屑。横截面的速度云图如图6所示。由图可知,木屑周围的气流速度约为V0=3.7 m/s。而实际生产中风机提供的风速远大于V0,通常为12～14 m/s[12]。这是因为通常情况下,设备存在很多死区,气流不经过这些死区,比如尘罩底部。即使风机的风速很快,但这些死区的气流速度依然很低,很难达到满意的除尘效果。

图6 木屑周围流速云图

根据表3的仿真数据绘制流速与作用力的图表,并用二次多项式对流速和作用力进行拟合,如图7所示。

4 结论

本文选取青城机械木工刨床的切屑作为研究对象,利用FLUENT得到一定气流速度情况下在木材切屑上产生的作用力,并借助定向优化求解器Direct Optimization得出在木材切屑上产生的作用力克服木屑重力时对应的气流速度和出口负压。得出如下结论:

(1)木屑周围的气流速度达到V0=3.7 m/s时,气流作用力大于木屑重力,此时气流可以带走木屑。

(2)实际生产中,由于设备存在各种死区,使得风机风速远大于V0才能达到满意的除尘效果。

(3)气流速度与其作用在木屑上的力近似满足二次方关系,二次多项式为F= 4E-06V2+ 9E-06V- 2E-06。

以上结论可为青城机械木工刨床的结构设计以及整机吸尘能力的优化设计提供一定的参考依据。