基于响应面的直线导轨性能参数与矫直行程预测模型仿真

王一函,凌 鹤

(武汉理工大学 机电工程学院,湖北 武汉 430070)

直线导轨作为机床的核心导向部件对制造精度有着重要影响[1]。近十年来,我国滚动功能部件发展迅速,但与发达国家相比仍有明显的差距,具体表现在精度和精度保持性较差[2]。精度保持性要求导轨有较高的硬度、刚度和耐磨性,为满足性能要求,直线导轨加工过程中通常会经过热处理工艺,随之而来的热变形会对导轨的几何精度产生影响[3]。而直线导轨的几何精度是导轨精度的重要指标,主要表现为在水平面内和垂直面内的直线度[4]。因此,矫直工艺在直线导轨生产工艺中不可或缺。

针对不同的材料和使用性能要求,直线导轨选择的热处理工艺方法有感应淬火、火焰淬火、接触电阻加热淬火、电解液表面淬火、激光淬火等[5]。淬火后直线导轨表面会形成一定厚度的淬硬层,其组织由表层至里层分为完全淬火区、不完全淬火区、热影响区和基体4个区域,不同区域内组织构成不同[6]。将具有规定硬度界限值的心部区域到工件表面的垂直距离称为有效淬硬层深度,在研究淬火导轨矫直问题时,通常将淬硬层视为在有效深度内力学性能稳定的均值组织。

位于矫直工艺前且必不可少的热处理工艺对矫直行程预测的影响分为两方面:一方面,淬火热处理过程会在导轨表面形成淬硬层,使工件产生组织差异,淬硬层的性能对矫直行程预测有着重要影响。另一方面,由于我国热处理技术水平较低,导轨热处理后工件品质参差不齐,即使是同一批次生产的导轨性能参数也并不完全相同,而是存在一定程度的波动,性能参数的差异直接影响矫直行程预测精度[7]。

笔者以单淬硬层分布的直线导轨为研究对象,以考虑淬硬层的直线导轨矫直行程预测模型为基础,采用响应面分析方法对不同性能参数的导轨进行有限元仿真,探究材料性能参数与矫直行程的关系,建立矫直行程预测仿真模型。

1 考虑淬硬层的直线导轨矫直行程预测模型

因淬火导致组织性能变化,单淬硬层分布的直线导轨在矫直过程中应力中性层相对于几何中性层会有少量偏移。分析时将淬硬层视为在有效深度内材质均匀的组织,则单表面淬火的直线导轨弯曲时的截面状态如图1所示。

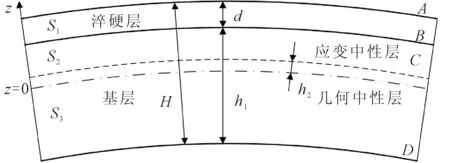
图1 单淬硬层分布的直线导轨弯曲过程中截面应变示意图

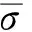
(1)

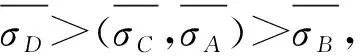
σ=

(2)

其中,λE为强化模量比。根据弹塑性理论,截面应力平衡,则:

λECσS2(z-e)]dz=0

(3)

因此可计算此时中性层偏移量e2:

(4)

用材料力学的积分法计算导轨弯矩,得:

(5)

(6)

在导轨矫直过程中,初始挠度为δ0、弹性系数为k的导轨其载荷和挠度关系如图2所示。矫直过程分为3个阶段:①弹性变形阶段,即OB段,对应的变形为δt;②弹塑性变形阶段,即BC段,对应的变形为δ∑;③弹性回复阶段,即CD段。

图2 压力矫直过程载荷挠度理论模型

其理论模型可表示为:

(7)

在弹性变形阶段,根据材料力学可计算三点简支的工件载荷挠度。在弹塑性阶段,其挠度示意图如图3所示。

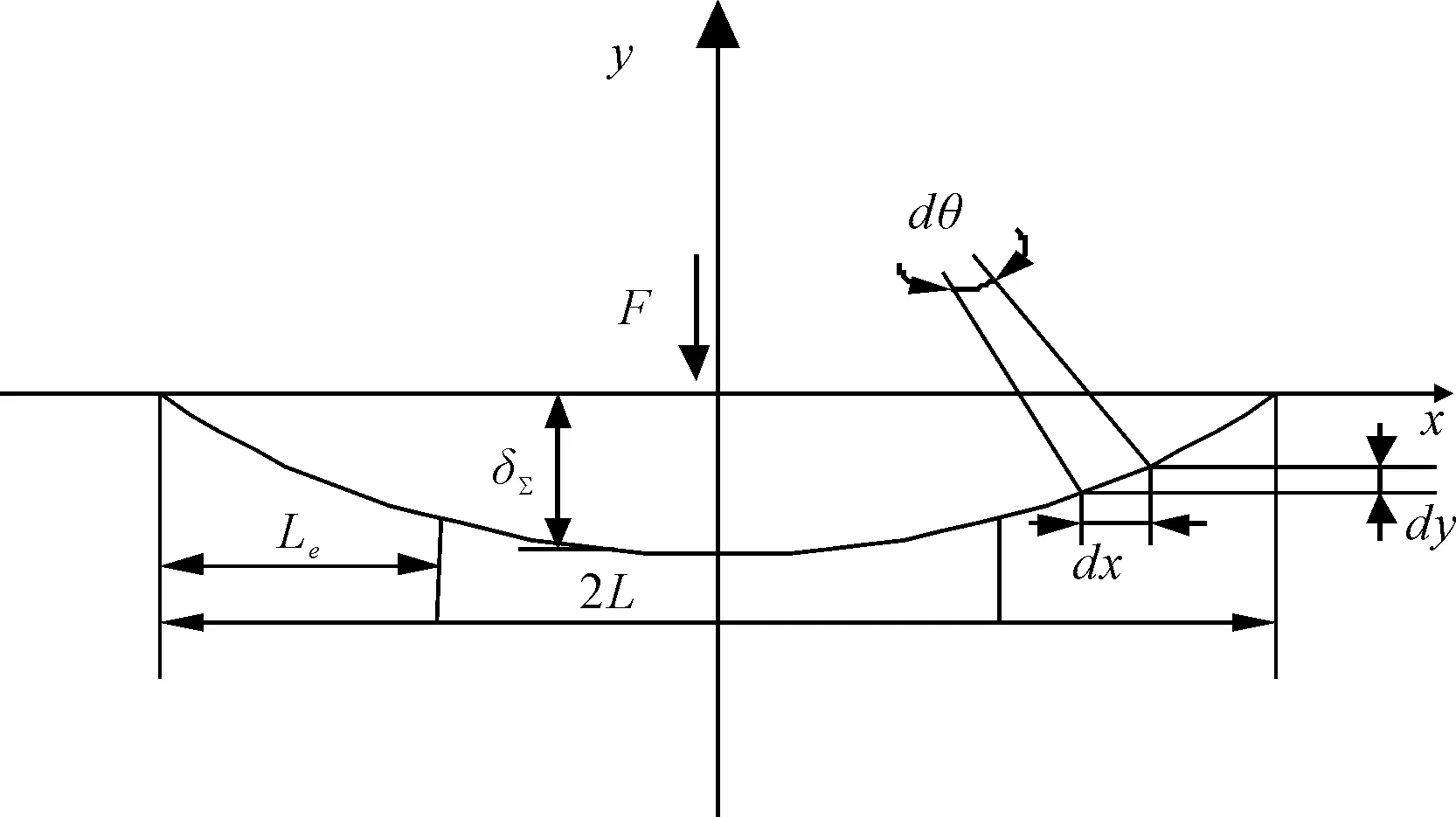
图3 导轨弯曲挠度示意图

如图3所示,设跨距为2L,以跨距中点为原点建立坐标系,设发生弹塑性弯曲的区域长度为2Le,坐标x处的弯矩为Mx,弯曲曲率为Ax,曲率比为Cx。则

Mx=(L-x)F/2

(8)

根据图3中几何关系可知:

dy=(L-x)dθ=(L-x)Axdx

(9)

因此直线导轨中间处矫直行程为:

(10)

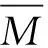
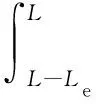
(11)

式中:N为弹塑性变形积分区间等分次数;xi=(L-Le)i/N;Cxi为xi处对应的弯曲曲率。

故式(7)所建立的载荷-挠度方程可补充如下[8]:

(12)

式中:Ft为弹性极限载荷;FP为塑性极限载荷,即图2中C点的载荷。

2 材料性能参数与矫直行程的数学模型

以单淬硬层分布的直线导轨为例,影响矫直行程预测的参数有初始挠度、屈服强度比和相对厚度。而残余挠度作为衡量矫直精度的标准,在拟合响应面的过程中需要被考虑。因此,将初始挠度、屈强比、相对厚度和矫直行程作为影响因子,将残余挠度作为响应值,采用Design-Export软件建立响应面模型,根据经验并参考其他学者研究[9-10],响应面影响因子及其上下域如表1所示。运用BBD(box-behnken design)实验设计方法根据表1设计实验组,并采用ANSYS软件进行仿真实验[11],实验组及仿真结果如表2所示。

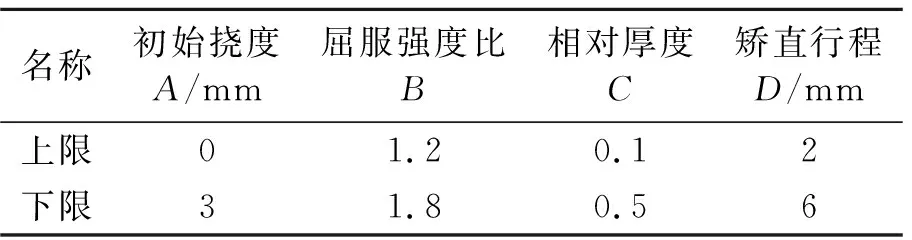
表1 影响因子及其上下域

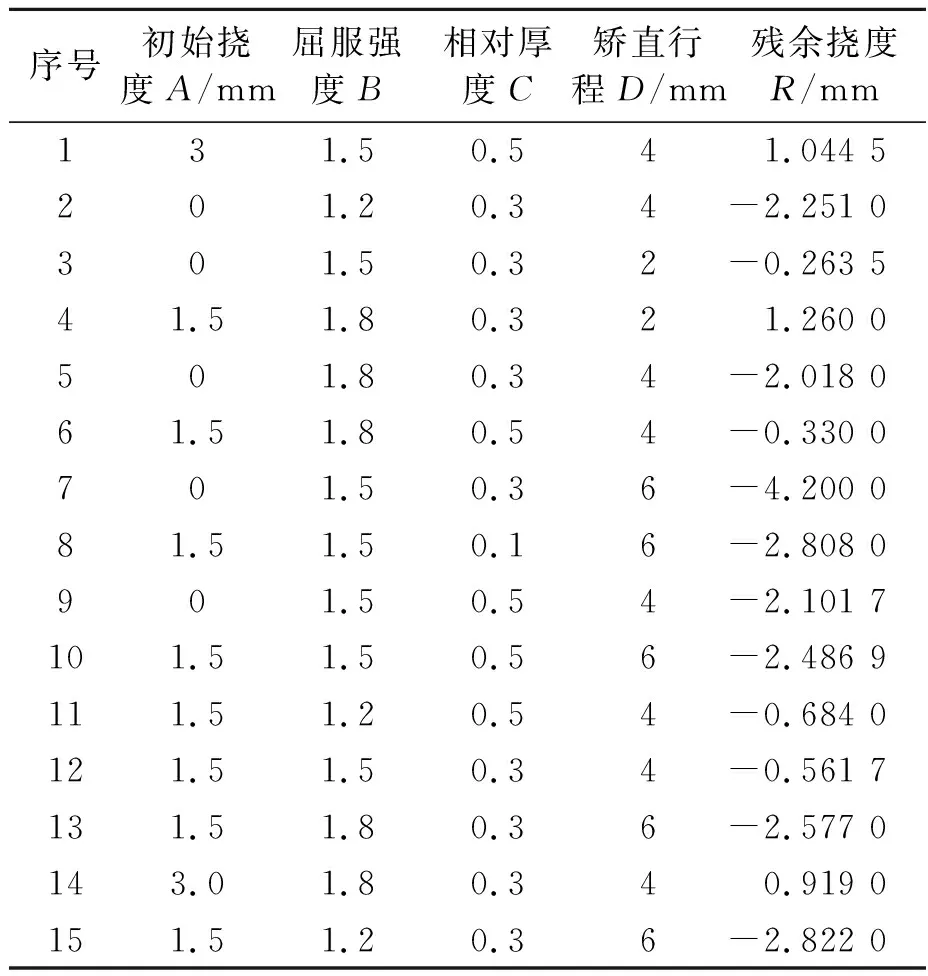
表2 响应面模型试验组和结果节选

采用Design-Expert软件对实验结果进行分析,通过对模型显著性检测、相关性检验的数据进行对比,得到最适合的回归方程为:

R=1.22A+0.33B+0.58C-0.61D-

0.039AD-0.03A2-0.041D2

(13)

使残余挠度为0,则可得到矫直行程与初始挠度、屈服强度比、相对厚度之件的耦合关系。对回归方程的显著性进行分析,F值和P值是检验显著性的标准,F值越大、P值越小则表示显著性越好[12]。本文所拟合模型P<0.000 1,表明模型显著性很好。对系数进行显著性检验,在总的作用因素中,得到A、B、C、D、AD、D2等6项系数表现显著,而A2的P值为0.069 3,表现接近显著。

表3 回归方程误差统计分析

适应性较好的响应面模型,其残差的正态概率分布应在一条直线上,实际值与预测值也应尽可能在一条直线上。由图4、图5可知,本文拟合模型适应性较好,可用于已知材料性能参数的直线导轨矫直行程预测。

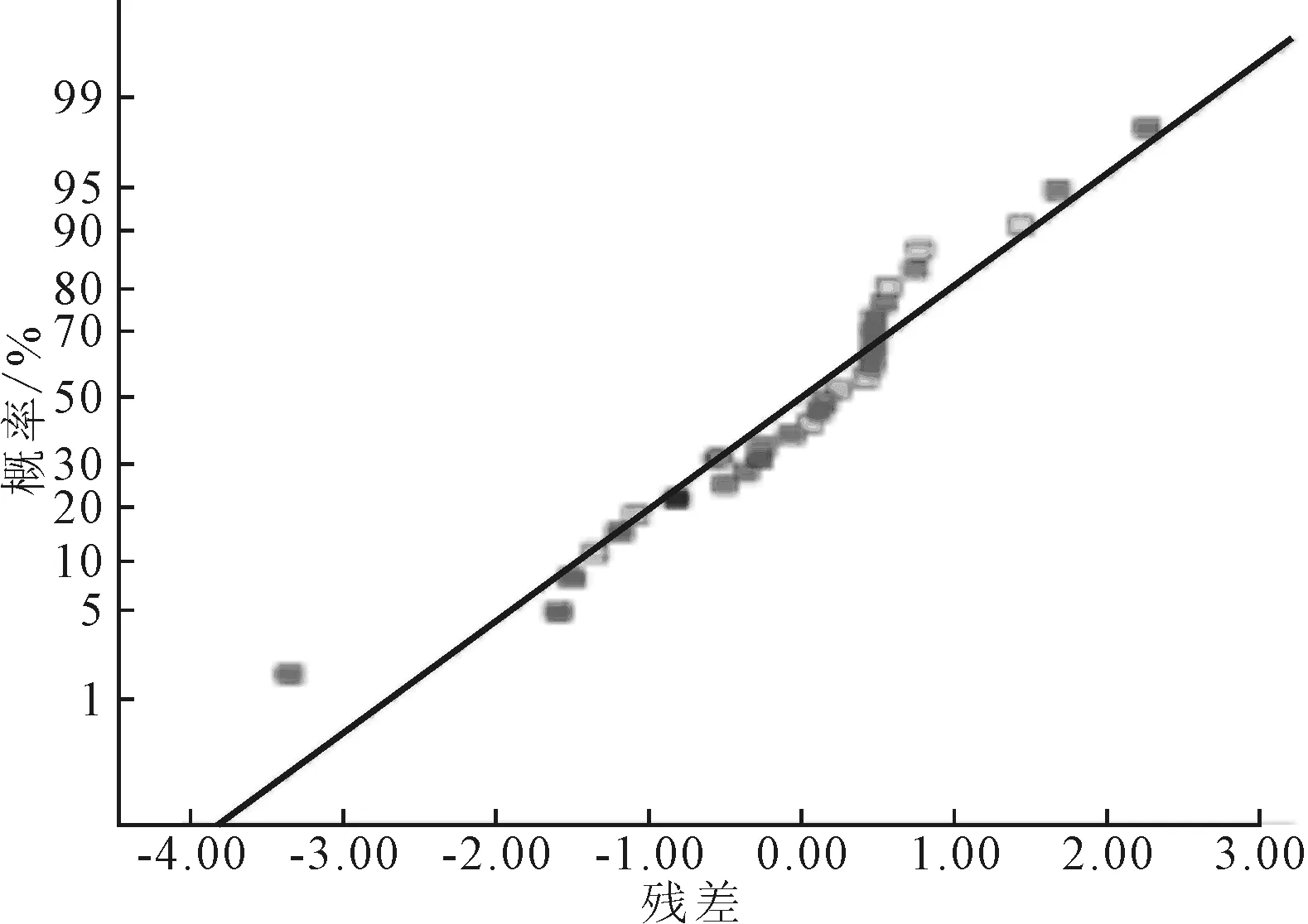
图4 残差的正态分布图

图5 预测值与实际值分布图

3 实验验证

选择4根材料为45钢、尺寸为20×20×400mm的直线导轨,将其分为两组,分别对其上表面进行高频、中频感应淬火,实验材料分组及其热处理工艺如表4所示。

表4 实验材料编号及其热处理工艺

选择DNS100万能材料试验机对以上导轨进行压力矫直实验,1号、3号导轨采用理论公式即式(12)计算矫直行程,2号、4号导轨采用回归方程即式(13)计算矫直行程,实验数据如表5、表6所示。

表5 G1组导轨矫直实验数据

表6 G2组导轨矫直实验数据

对比1号与2号导轨及3号与4号导轨,在达到相同精度情况下,采用回归方程计算矫直行程比采用理论公式计算矫直行程所需的矫直次数更少,证明了回归方程的可行性和正确性。

4 结论

通过探究单淬硬层分布的直线导轨矫直过程中应力分布,计算了应力中性层相对几何中性层的偏移量,并推导了单淬硬层分布的直线导轨矫直行程预测理论模型;引入矫直残余挠度作为响应值,利用ANSYS仿真数据拟合了初始挠度、淬硬层与基层屈服强度比、淬硬层相对厚度、矫直行程与残余挠度之间的响应面回归方程,间接建立了导轨性能参数与矫直行程之间的关系模型,模型显著性与误差分析显示,拟合方程很好地适应了矫直数据,经实验验证,能够进行更精确的矫直行程预测。