基于卡方跃迁策略的黑蜘蛛优化算法及应用

杜晓昕, 王振飞, 王 波, 王 浩, 郝田茹, 崔连和

(齐齐哈尔大学 计算机与控制工程学院, 黑龙江 齐齐哈尔 161006)

0 引言

随着现实世界许多的优化问题变得越来越复杂,传统的优化方法在解决这类问题时需要花费太多时间,并且不能有效解决.近年来研究人员受各种自然现象启发而提出的元启发式算法[1],例如模拟鸟群觅食的粒子群算法[2],借鉴生物界进化规律的遗传算法[3],受固体退火原理启发的模拟退火算法[4],模拟灰狼捕食猎物的灰狼优化算法[5]等,这些算法均具有求解速度快、求解精度高、鲁棒性强等优点,在解决现代优化问题上均具有较好的表现.黑蜘蛛优化算法(BWOA)是Pena Delgado等[6]于2020年提出的一种新的仿生元启发式优化算法,该算法模拟雄性黑蜘蛛选取最佳交配雌性伴侣的过程[7],具有参数设定少、全局寻优能力强等优点,引起了学术界的广泛关注,并被应用于工程优化[8]、特征选择[9]、参数优化[10]等诸多领域,成功解决了各种难题.

但与上述提到的其它元启发式优化算法一样,BWOA也存在易陷入局部最优、收敛精度低、全局勘探和局部开发失衡等问题,为了改善这些不足,傅彦铭等[11]提出一种基于角逐和改进信息素机制的多目标黑蜘蛛优化算法,采用动态分配种群的方法,改进信息素更新机制,引导待优化个体向种群间隙方向进行优化,增强算法的收敛速度和寻优能力.Xu等[12]提出了一种结合柯西重心逆差突变和黄金正弦引导策略的黑蜘蛛优化算法,基于双混沌图提高BWOA初始种群质量,并引入黄金正弦算法及柯西重心逆微分突变算子增加种群多样性,从而提高算法的搜索能力.Wan等[13]提出一种多策略黑蜘蛛优化算法,采用高斯混沌映射初始化种群,引入正弦余弦策略在迭代过程中对个体进行扰动并结合差分进化算法的变异方法,对适应度值较差的个体进行重组,以提高算法的收敛速度.

综上所述,这些改进策略虽然从不同角度提高了算法的寻优能力,然而到目前为止对BWOA的改动一方面难于帮助黑蜘蛛跳出局部最优,另一方面难以在全局勘探和局部开发方面取得平衡,针对这些问题,本文提出了一种基于卡方跃迁策略的黑蜘蛛优化算法(CTBWOA),首先采用佳点集初始化种群来替代随机初始化种群,使黑蜘蛛更加均匀地分布于初始解空间,增强初始种群的遍历性;其次提出卡方跃迁策略,在黑蜘蛛陷入局部最优时,帮助黑蜘蛛跳出局部最优,避免算法早熟收敛;再次通过自选取运动策略,以平衡算法的勘探和开发能力;最后采取三蛛竞争及回溯机制,改进低信息素黑蜘蛛替换策略,以增强算法多样性,提高算法收敛速度和精度.

本文最后将CTBWOA应用到了SVM的参数优化中,把SVM的参数作为黑蜘蛛的位置信息,以SVM分类准确率作为优化准则建立目标函数,通过迭代得到最优参数和最优分类准确率,实现对支持向量机核参数和惩罚参数的优化选取,以提高支持向量机的分类精度和泛化能力.仿真实验结果表明该方法优化的SVM其分类准确率有了明显提高,从而证明了该优化算法的可行性与有效性.

1 黑蜘蛛优化算法

本节介绍了黑蜘蛛优化算法的数学模型,描述了黑蜘蛛从随机解出发,通过不同的运动策略和信息素策略迭代寻找最优解的过程.

1.1 种群初始化策略

为了保证BWOA的全局搜索能力,将种群数为N的个体初始化为:

(1)

式(1)中:D表示待解决问题的维度,N为黑蜘蛛的个数,矩阵中的每一行代表一个黑蜘蛛的当前位置,即对应一个解,其中第i个黑蜘蛛的初始化求解公式为:

(2)

式(2)中:UB表示决策变量的上界,LB表示决策变量的下界,rand为从0到1的随机数.

1.2 运动策略

黑蜘蛛在蛛网内按照线性和螺旋的方式进行移动,其数学模型为:

(3)

1.3 信息素替换策略

信息素在黑蜘蛛的交配中发挥着非常重要的作用,同时黑蜘蛛的饮食和信息素之间也具有重要联系[14].吃饱的雌性黑蜘蛛信息素高于饥饿的雌性黑蜘蛛,雄性黑蜘蛛更倾向于寻找信息素高的雌性黑蜘蛛,因为这降低了同类相食的发生概率.因此,信息素低的雌性黑蜘蛛并不是雄性黑蜘蛛的首选.在BWOA中,黑蜘蛛的信息素求解公式为:

(4)

式(4)中:pheromone(i)表示第i只雌性黑蜘蛛的信息素,这个值为从0到1的浮点数;fitnessmax和fitnessmin分别是此次迭代中最差和最优的适应度值,fitness(i)是第i个搜索代理的当前适应度值.规定当信息素值等于或小于0.3时,表示雌性黑蜘蛛正处于饥饿状态,为了避免同类相食,雄性黑蜘蛛就不会选择它进行交配,而是把它替换为另一只黑蜘蛛,其替换公式为:

(5)

2 基于卡方跃迁策略的黑蜘蛛优化算法

2.1 基于佳点集的种群初始化策略

初始种群的质量会影响算法的求解速度,而优秀的种群初始化策略能够使种群个体更均匀的遍历整个搜索空间,以此增强种群的多样性,提高算法收敛速度,为算法的全局搜索奠定基础.本文引入佳点集对种群进行初始化,有效的提高了算法在解空间上的遍历能力.

佳点集由华罗庚等[15]提出,其原理为:设Gs为s维欧式空间的单位立方体,如果r∈Gs,对于:

(6)

其偏差满足:

φ(n)=C(r,ε)nε-1

(7)

则称Pn(k)为佳点集,r为佳点.式(6)中: (r1(n)·k)代表取小数部分,式(7)中:ε为任意正数,C(r,ε)是只和r,ε有关的常数,n表示点数,而r为:

r={2 cos(2πk/p),1≤k≤s}

(8)

式(8)中:p是满足(p-3)/2≥s的最小素数.

设搜索空间为2维,种群规模为1 000,取值范围为[0,1],采用佳点集初始化种群与随机初始化种群的分布图如图1和图2所示.

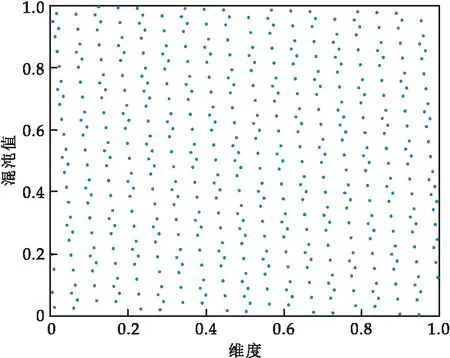
图1 佳点集初始化种群分布

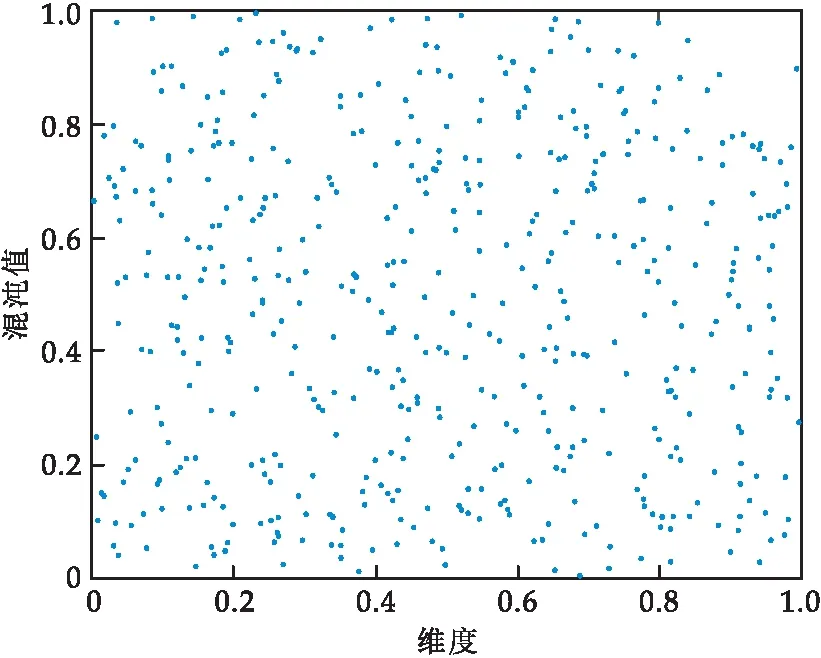
图2 随机初始化种群分布

图3为在上述条件下,采用佳点集和随机初始化的频数分布直方图.图中棕色部分为随机初始化的频数分布,蓝色部分为采用佳点集的频数分布,咖啡色为两种方法的重叠区域,从中可以看出佳点集生成的种群在各个区间中频数均接近一百,而随机初始化分布生成的种群在区间中频数最高为一百一左右,最低则达到了八十,上下限差距较大.因此采用佳点集初始化策略,能够使种群个体分布更加均匀,增强算法的遍历性,从而更好地提高算法收敛速度及全局搜索能力.

图3 佳点集和随机种群初始化频数分布直方图

2.2 卡方跃迁策略

在标准黑蜘蛛优化算法中,黑蜘蛛在种群迭代过程中,不管是通过运动策略或者信息素策略进行位置更新,都会趋向于靠近当前种群中的最优黑蜘蛛,这固然会增强算法的收敛能力,提高算法的收敛速度,但同时会降低算法的多样性,使得算法过早收敛,导致黑蜘蛛陷入局部最优无法跳出.针对上述问题,提出卡方跃迁策略,当黑蜘蛛陷入局部最优无法跳出时,通过卡方跃迁机制带领黑蜘蛛离开局部最优,提高算法的寻优能力.卡方跃迁策略的公式如式(9)所示:

Xidt+1=Xidt+γ⊕L(λ)

(9)

式(9)中:Xidt+1表示第i只蜘蛛在t+1次迭代中第d维的值,γ为步长控制系数,L(λ)为莱维飞行[16]的随机搜索路径,具体描述为:

(10)

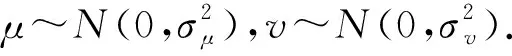
(11)

式(11)中:n表示自由度,t为当前迭代次数,tmax为最大迭代次数,fn(x)为卡方分布概率密度函数,公式为:

(12)

式(12)中:Γ(n/2)为伽马函数,即:

(13)

卡方分布是统计学中最重要的分布之一,定义为如果n个随机变量X相互独立,都服从N(0,1),则称X服从自由度为n的卡方分布.本文利用卡方分布在自由度为2时函数非线性递减的特性,将其融入到自适应步长的求解中.实现在算法迭代初期,当黑蜘蛛处于搜索阶段时,通过大步长搜索来更新位置,加快黑蜘蛛找到最优解的速度;在迭代后期,黑蜘蛛进入开发阶段时,使用较小的步长进行位置更新,以提高解的精度.γ的变化图像如图4所示.

图4 γ变化曲线

2.3 自选取运动策略

在原始的黑蜘蛛优化算法中,算法通过值为0.3的常量a控制黑蜘蛛在蛛网内的运动方式,当随机数小于等于a时黑蜘蛛采用线性运动,随机数大于a时进行螺旋运动.导致黑蜘蛛大概率进行螺旋运动,这固然会提高算法的全局勘探能力,但同时算法以小概率进行线性运动,大大降低了算法的局部开发能力,所以常量a不能有效平衡黑蜘蛛的运动方式,并且使得标准BWOA算法的全局搜索能力和局部开发能力失衡.因此本文基于Sigmoid[19]函数提出了一种非线性递增的参数a,以平衡算法的勘探和开发.改进后的参数a求解公式为:

(14)

式(14)中:b为常数-5,t为当前迭代次数,tmax为最大迭代次数,c是值为0.3的平衡因子.改进后的参数a随迭代次数的增加其值的变化情况如图5所示.

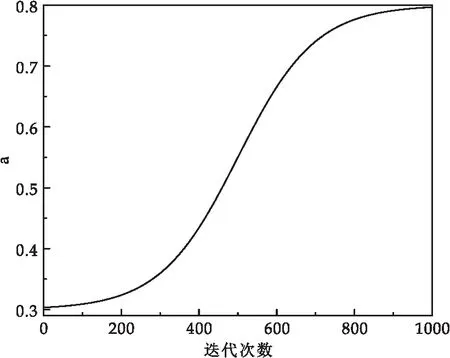
图5 非线性递增参数a变化曲线

从图中可以看出本文提出的非线性递增参数a在算法迭代前期数值变化幅度及速度较小,即蜘蛛大概率选取螺旋运动策略,扩大蜘蛛的搜索范围;迭代中期参数a上升速度明显,此时黑蜘蛛对运动策略的选取概率相近,以平衡算法的勘探和开发能力;迭代后期,参数a在较长时间内保持较大值且变化幅度和速度也较小,使得蜘蛛大概率选取线性运动策略,加强算法的局部搜索能力.

2.4 三蛛竞争及回溯学习机制

信息素替换策略利用公式(4)将低信息素的雌性黑蜘蛛替换掉,以寻找获取高信息素的黑蜘蛛.但是这种替换随机性较强,从式(4)可以看出,当随机获取的两只蜘蛛信息素较低时,替换之后的蜘蛛信息素值也会相对较低,则此次替换无意义.因此提出三蛛竞争及回溯学习机制,首先从当前种群中随机选取三只雌性黑蜘蛛,通过竞争选取其中信息素最高的个体作为一个交流学习对象,其次获取当前种群中的最优黑蜘蛛作为另一个交流学习对象,最后分别与通过回溯机制获取的被替换蜘蛛的个体最优经验,即历史最优位置信息进行交流学习,从而引导此次替换朝着最优值方向发展,以提高算法的收敛速度.三蛛竞争及回溯机制的示意图如图6所示.

改进后的低信息素黑蜘蛛替换公式为:

(15)

2.5 CTBWOA算法的实现

对标准的黑蜘蛛优化算法进行改进后,得到的CTBWOA算法流程图如图7所示.

图7 CTBWOA算法流程图

CTBWOA算法伪代码如下:

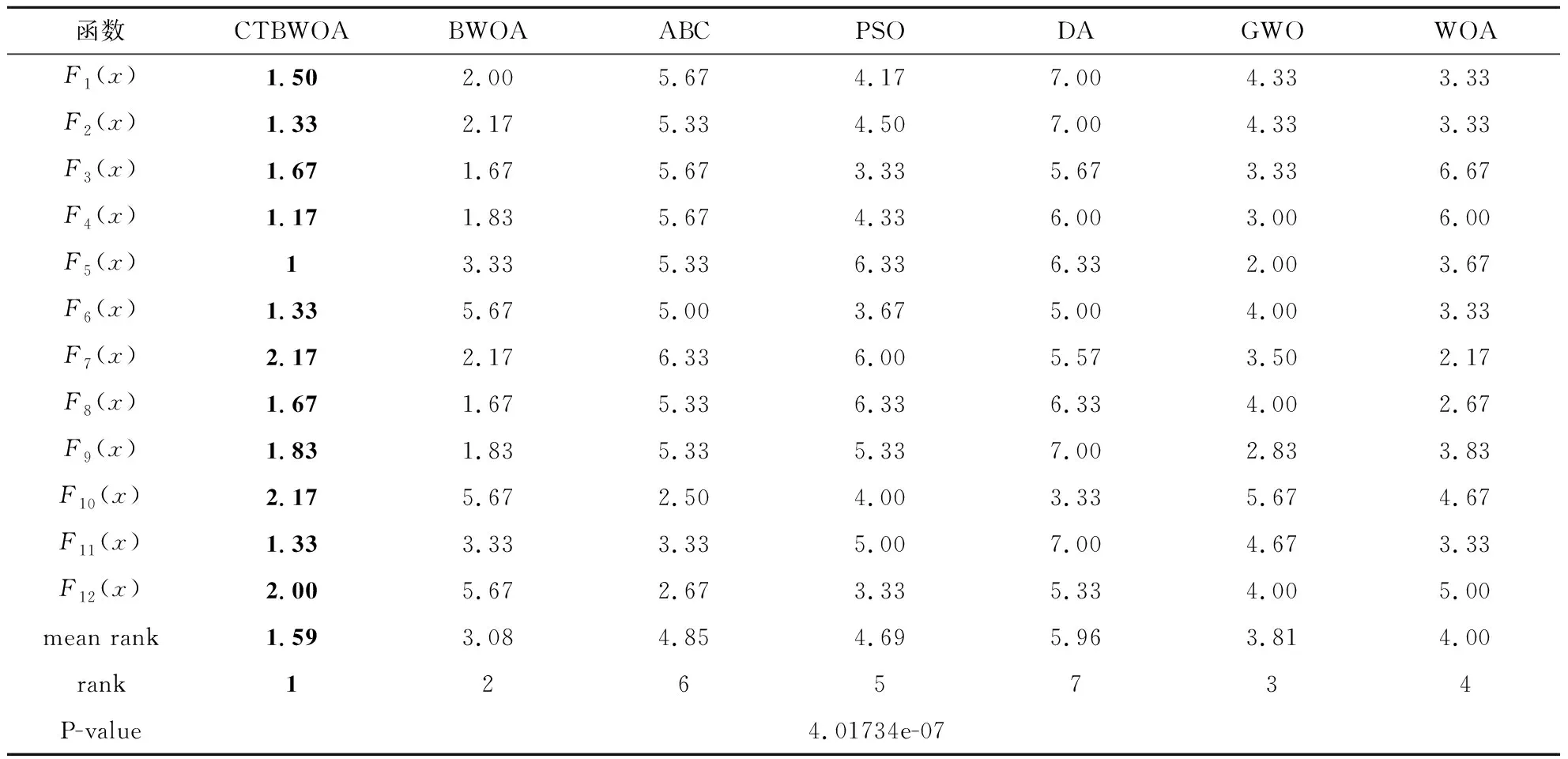
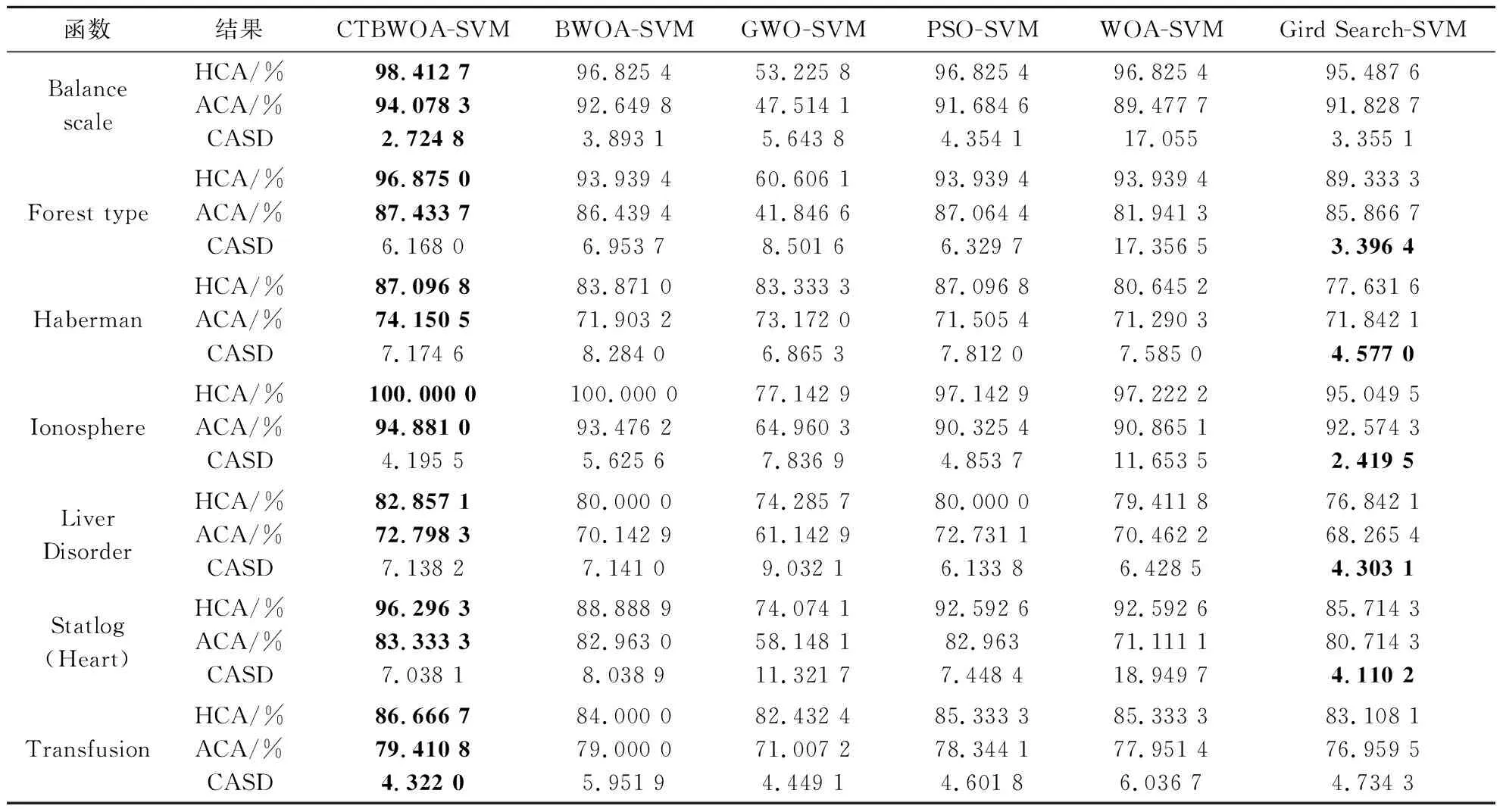
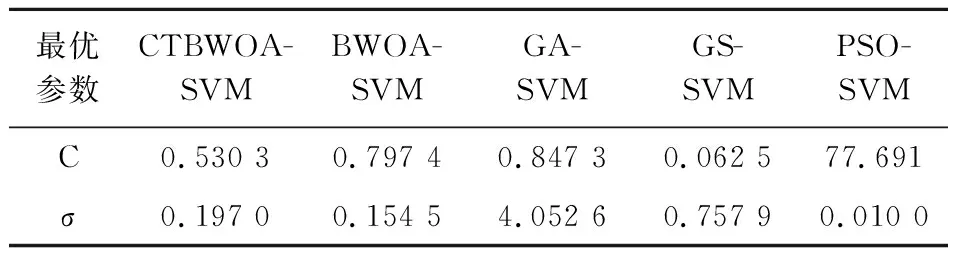
CTBWOA算法伪代码输入:目标函数F(x)、种群规模N、最大迭代次数tmax输出:最佳解xBestStep1:采用佳点集初始化黑蜘蛛种群XStep2:while(t

3 实验结果与分析

3.1 CTBWOA的仿真实验与分析

3.1.1 基准测试函数及对比算法参数设置

为保证实验的有效性和公正性,将所提算法分别与原始黑蜘蛛优化算法BWOA、人工蜂群算法(Artificial Bee Colony Algorithm,ABC)[20]、粒子群算法(Particle Swarm Algorithm,PSO)[21]、蜻蜓算法(Dragonfly Algorithm,DA)[22]、灰狼优化算法(Grey Wolf Algorithm,GWO)[23]、鲸鱼优化算法(Whale Optimization Algorithm,WOA)[24]进行对比分析,所有算法的初始参数见表1所示.

表1 对比算法的初始化参数

本文仿真实验中每种算法的种群规模为50,最大迭代次数为500.选取12个典型标准测试函数[25]进行仿真试验,其中F1～F5为单峰函数,用于检验算法的收敛速度和求解精度;F6～F12为多峰函数,用于检验算法的全局搜索能力.表2给出了12个测试函数的维度、搜索空间和最优值.

表2 标准测试函数详细信息

3.1.2 实验结果

为了避免实验结果的偶然性,本实验对每一种算法都进行了100次独立实验,并计算其最优值(Best)、平均值(Mean)和标准差(Standard Deviation,Std),其结果如表3所示.其中最优值为算法在100次独立运行时获得的最优解,即最小值;平均值为算法对每个函数多次运行后的平均情况,平均值越低表明算法效果越好;标准差代表算法的稳定性,值越小,说明算法越稳定.本文仿真实验在AMD Ryzen 7-5800H CPU、3.20 GHz、16.0 GB内存、Windows 11(64位)操作系统 、MATLAB R2021a条件下进行.

表3 7种算法对12个函数的运行结果比较

实验结果如表3所示,其中粗体表示各函数中最优值、平均值和标准差的最小值.由表3可知,对于单峰函数F1～F5,CTBWOA算法在函数F1、F2、F3、F4中均找到了理论最优值,且标准差为0,虽未找到函数F5的理论最优值,但与其他算法相比,CTBWOA算法得到的最优值最接近函数的理论最优值,并且取得了最好的平均值和标准差.这表明CTBWOA算法与其他算法相比具有更强的开发能力.

对于具有许多局部最小值的多峰函数F6～F12来说,CTBWOA算法在函数F7、F9、F11、F12中均找到了理论最优值,而且在函数F8、F10中获取的最优值也优于其他算法,证明算法具有较强的勘探能力.除函数F6外,CTBWOA算法均得到了最小的最优值、平均值和标准差,进一步证明了和其他算法相比,其具有更高的收敛精度和稳定性.

为了更加直观地反映CTBWOA算法的性能,图8给出了7个算法在12个测试函数上的收敛曲线.不管是对于单峰函数F1～F5,还是对于多峰函数F6～F12,CTBWOA算法的收敛速度均明显优于标准BWOA算法和其他经典算法,这得益于本文采取佳点集的初始化策略,使黑蜘蛛分布更加均匀,为算法的全局寻优奠定基础,以及自选取运动策略对算法的运动策略进行改动,进一步平衡了算法的局部搜索能力和全局搜索能力,提高了算法的收敛速度.同时从图8中可以看出,标准BWOA算法和其它经典算法均存在易陷入局部最优的问题,即收敛曲线在搜索到理论最优值之前趋于平缓,不能找到函数最优值,而CTBWOA算法的收敛曲线则出现波动的情况,说明在卡方跃迁策略的作用下,能更好的帮助算法跳出局部最优解,防止算法过早收敛.这些结果表明,CTBWOA算法相对于其它五种算法来说,就有更高的寻优能力.

图8 CTBWOA算法与其他经典算法的收敛效果对比图

3.1.3 Friedman检验

除了给定的评估指标(最优值、平均值和标准差)之外,本文还采用Friedman检验[25],应用统计学方式对七个算法的性能进行测试排序,以进一步验证CTBWOA与其它算法的显著性差异.

首先获取每个算法在12个测试函数中的最优值与最差值;其次分别求出各个算法在每个测试函数中的平均排名;最后计算最终排名,其值越小,则代表算法性能越优.测试结果如表4所示.

表4 7种算法的Friedman检验结果排名

表4中粗体为排名最小的值,其中P-value表示渐进显著性,若其值小于0.01,则说明各项数据之间存在显著性差异.结果表明与其他算法相比,所提CTBWOA算法在测试中排名第一,且P-value为4.01734e-07,远远小于0.01这表明CTBWOA与其他算法之间存在显著差异.总体上说,CTBWOA可以产生高质量的解决方案,这进一步说明了本文算法改进策略的有效性.

3.1.4 CTBWOA算法的时间复杂度分析

时间复杂度体现的是算法的运行效率,是评价算法性能优劣的重要因素.评价改进的算法是否具有可行性和有效性,一方面是看改进后的算法寻优能力是否具有较大提升,另一方面是看算法时间复杂度是否较大程度的高于原始算法.

在标准BWOA中,假设算法的种群规模为n,求解问题维度为d,最大迭代次数为tmax,则BWOA在初始化阶段的时间复杂度为:

T1=O(n×d)

(16)

假设n1和n2分别为进行线性运动和进行螺旋运动的黑蜘蛛总数,n3为通过信息素替换策略替换的黑蜘蛛总数,则BWOA在搜索和勘探阶段的时间复杂度为:

T2=O((n1+n2+n3)×d×tmax)=
O(n×d×tmax)

(17)

因此,BWOA的时间复杂度为:

T=T1+T2=O(n×d×tmax)

(18)

在CTBWOA中,生成佳点集所用的时间为k1,则其初始化阶段的时间复杂度为:

T3=O(n×d+k1)=O(n×d)

(19)

假设CTBWOA生成卡方自适应步长γ的时间为k2,种群中依据式(9)进行卡方跃迁的黑蜘蛛个数为n4,生成非线性递增参数a的时间为k3,引入三蛛竞争及回溯学习机制后被替换的黑蜘蛛个数为n5,每只被替换黑蜘蛛竞争及回溯学习花费时间为k4,此时CTBWOA在勘探和开发阶段的时间复杂度为:

T4=O((n4+n5)×d×tmax+n×d×tmax+
k1+k2+k3)=O(n×d×tmax)

(20)

综上可得CTBWOA的时间复杂度为:

T′=T3+T4=O(n×d×tmax)

(21)

由此可知,CTBWOA算法时间复杂度与标准BWOA算法时间复杂度一致,这表明本文针对BWOA算法的不足而提出的改进策略并未增加算法的时间复杂度.

3.2 CTBWOA-SVM原理及仿真与分析

3.2.1 CTBWOA-SVM原理

支持向量机(SVM)[26]是20世纪90年代中期发展起来的一种基于统计学习理论的VC维和结构风险最小化原理的机器学习方法,由Cortes和Vapik提出.SVM是应用最广泛的分类算法之一,其核心思想就是在特征空间中根据间隔最大化原则寻找一个最优超平面,即选取的超平面应该与离他最近的样本点之间的距离尽量大,最终转化为一个凸二次规划问题来求解.支持向量机在处理高维数据时拥有精度高、学习能力强等优势,因此被广泛应用于语音识别[27]、图像过滤[28]、人脸检测[29]、手写体识别[30]和疾病诊断[31]等领域.

在利用支持向量机进行分类的过程中,模型参数(惩罚因子C和核函数参数)的选择对支持向量机的预测精度和分类性能有至关重要的影响.传统的参数选择方法,如网格搜索法[32]、梯度下降法[33]等存在搜索时间较长、参数设定不准确等问题.本文采用CTBWOA算法优化SVM模型中两个参数(这里选取机器学习领域较为流行的高斯核函数[34]作为SVM的核函数),即惩罚因子C和核函数参数σ,此方法简记为CTBWOA-SVM.CTBWOA-SVM的目标函数是SVM的分类准确率,CTBWOA找到的最佳位置就是SVM的最佳参数.

CTBWOA-SVM算法具体实现步骤如下:

步骤一初始化最大迭代次数tmax、种群规模N、决策变量的下界LB和上界UB(对应SVM的惩罚因子C和核函数参数σ),将数据集中的数据进行归一化处理.

步骤二采用佳点集初始化黑蜘蛛的位置信息.

步骤三将黑蜘蛛的位置信息作为SVM的参数,把分类准确率作为目标函数进行寻优,得到适应度值.

步骤四通过自适应运动策略获取参数a的值,确定黑蜘蛛的运动方式,即进行线性运动或是螺旋运动.

步骤五计算黑蜘蛛的信息素值,并根据三蛛竞争及回溯机制替换低信息素的黑蜘蛛.

步骤六判断黑蜘蛛是否需要进行卡方跃迁,如果是则更新黑蜘蛛的位置信息以及个体最优和全局最优.

步骤七将新产生的位置信息作为SVM的参数值输入到SVM中,进行十折交叉验证计算适应度值,并更新最高适应度值及最优参数组合.

步骤八判断是否达到最大迭代次数,如果是则输出最优参数组合及分类准确率,否则转到步骤四,进行下一次迭代寻优.

3.2.2 仿真实验数据

为了验证CTBWOA-SVM的有效性,本文选取基于原始BWOA优化的支持向量机(BWOA-SVM)、基于GWO优化的支持向量机[35](GWO-SVM)、基于PSO优化的支持向量机[36](PSO-SVM)、基于WOA优化的支持向量机[37](WOA-SVM)、基于网格搜索优化的支持向量机[38](Gird Search-SVM)作为对比,并选取了来自UCI(University of California at Irvin)数据库中的7组数据集进行仿真实验.分别从最高分类准确率、平均分类准确率和分类准确率标准差(分类准确率为各算法对应的SVM模型在测试集上的结果)这三个方面对所提方法进行分析.数据集的相关信息如表5所示,这些数据集被广泛应用于比较不同分类模型的性能.

表5 数据集详细信息

在仿真实验过程中,首先设置种群大小为20,最大迭代次数为50;其次对数据进行归一化处理,使数据属性具有相同的度量尺度,以消除奇异样本数据对模型的不良影响;最后使用十折交叉验证法,把数据集随机分为十份,依次将其中的一份作为测试集,剩余的九份作为训练集,以获取测试结果.为了排除测试结果的偶然性,这里使每种算法在每个数据集上独立运行20次.

3.2.3 结果分析

表6是CTBWOA-SVM与BWOA-SVM、GWO-SVM、PSO-SVM、WOA-SVM和Gird Search-SVM六种方法在不同的数据集上的最高分类准确率(Highest Classification Accuracy,HCA)、平均分类准确率(Average Classification Accuracy,ACA)及分类准确率标准差(Classification Accuracy Standard Deviation,CASD).通过观察可以看出,本文所提算法在7个数据集上的最高分类准确率及平均分类准确率均高于其他六种算法.在处理Forest type、Ionosphere、Statlog (Heart)这三个高维数据集时,CTBWOA-SVM相较于其他四种群智能算法优化的SVM,取得了最小的标准差,即CTBWAO-SVM在处理高维数据时,具有较高的稳定性,但在处理Haberman、Liver Disorder这两个低维数据时,以及和传统SVM相比,取得的标准差相对较大,即稳定性较差,这将作为以后的研究重点.

表6 5种算法对7个数据集的分类结果比较

图9为5种群智能算法优化的SVM在7个不同数据集上的适应度值收敛曲线,清晰地表现出了每个模型在不同数据集上的搜索收敛过程.由图9可知,不管是低维数据还是高维数据,本文所提算法在收敛速度、收敛精度上都优于其他算法.

图9 5种算法在7个数据集下的适应度值收敛曲线图

综上表明基于卡方跃迁策略的黑蜘蛛优化算法优化的支持向量机具有更高的分类准确率,在优化SVM的参数选取方面,具有一定的可行性和有效性,从而为SVM的参数优化提供了一种可行的方法.

4 CTBWOA-SVM在乳腺癌诊断中的应用

癌症是一组可影响身体任何部位的多种疾病的通称,据世界卫生组织报道,癌症是全世界的一个主要死因.据国际癌症研究机构发布的2020年全球癌症发病率和死亡率估计显示,2020年新增癌症病例1 930万例,癌症死亡1 000万例[39].2020年全球女性新发癌症923万例,占总数的48%,其中乳腺癌新发226万例,死亡68.5万例,乳腺癌新增病例不仅远超女性其它癌症类型,而且首次正事取代肺癌(220万例)成为全球第一大癌症,占所有新增癌症患者的11.7%.尽管情况危急,但幸运的是,研究表明,早期发现可以大大降低乳腺癌的死亡率(40%或更多)[40],因此,癌症的早期诊断对于患者得到及时、正确的治疗至关重要.

为进一步验证CTBWOA的有效性和可行性,使用William博士提供的威斯康星州乳腺癌数据集[41]进行仿真实验.数据集中包含699个样本,其中有241个恶性样本和458个良性样本.每个样本又都含有9个特征,分别是Clump thickness(肿块厚度)、Uniformity of cell size(细胞大小均匀度)、Uniformity of cell shape(细胞形状均匀度)、Marginal adhesion(边缘粘滞性)、Single epithelial cell size(单层上皮细胞大小)、Bare nuclei(原子核裸露程度)、Bland chromatin(染色质颜色)、Normal nucleoli(核仁正常情况)、Mitoses(有丝分裂情况).为得到更好的预测效果,本文在保留数据真实性的基础上,剔除了16个存在缺失值的数据样本,最终得到实验样本为683个.

通过计算其分类准确率(Accuracy)、分类精度(Precision)、召回率(Recall)、总准确率(G-mean)、F度量(F-measure)、马修斯相关系数(MCC)和AUC来评估CTBWOA-SVM的性能.并与BWOA-SVM、基于遗传算法优化的SVM(GA-SVM)[42]、基于网格搜索优化的SVM(GS-SVM)[38]、基于粒子群算法优化的SVM(PSO-SVM)[43]、基于主成分分析的SVM(PCA-SVM)[44]、最原始的SVM(SVM)进行对比.其中原始SVM和PCA-SVM算法的参数设定为固定值,C为100,σ为4,其余算法均对SVM的参数进行了优化,得到的最优参数如表7所示.随机选取90%的数据作为训练集,剩下的10%作为测试集,同时为了排除实验结果的偶然性,进行10次独立重复试验取平均值,具体结果如表8所示.

表7 最优C、σ参数值

表8 算法性能度量结果

由表8可知,在所有的优化算法中,基于卡方跃迁策略的黑蜘蛛优化算法优化的支持向量机(CTBWOA-SVM)与其他算法的相比,在分类准确率、分类精度、MCC、AUC等各个评价指标上均取得了最优值,其中分类准确率与原始SVM相比提高了2.5%,可以看出该方法能够为乳腺癌辅助诊断的决策提供有效支持,从而提高医疗机构的诊断准确率.

5 结论

针对原始黑蜘蛛优化算法存在的性能不足,本文提出了一种基于卡方跃迁策略的黑蜘蛛优化算法(CTBWOA).首先在初始化阶段,采用佳点集初始化种群策略代替随机种群初始化策略,使种群均匀遍历在解空间中,提高了算法的全局搜索能力;其次提出卡方跃迁策略,帮助黑蜘蛛及时跳出局部最优位置,避免黑蜘蛛早熟收敛;为了平衡算法的勘探与开发,提出自选取运动策略,优化黑蜘蛛运动方式的选取,提高算法的收敛速度;最后提出三蛛竞争及回溯学习机制,提升替换黑蜘蛛的质量以提高算法寻优能力.通过对CTBWOA在12个标准测试函数上进行测试,结果表明CTBWOA与BWOA、ABC、PSO、DA、GWO、WOA相比,具有更快的收敛速度、更高的收敛精度以及更高的稳定性.并将CTBWOA应用到了SVM的参数优化中,仿真实验表明,与其它算法优化的SVM及原始SVM相比,CTBWOA-SVM具有更高的分类准确率,从而为支持向量机的惩罚参数及核函数参数选取提供了一种可行的方法,这进一步体现了CTBWOA的有效性.对于未来的研究,我们将探索更优秀的优化方法来优化BWOA,同时将算法应用到实际工程问题中,使其具有更好地应用价值.