“RMFS”拣选系统的订单分批优化

杨 玮, 郑传辉, 李 然, 徐 丹

(陕西科技大学 机电工程学院, 陕西 西安 710021)

0 引言

随着互联网技术的迅猛提升,电商行业发展愈发繁荣,订单拣选效率备受关注,如何在紧凑的交货期内处理海量客户订单实现“快速交付”,不断提高客户满意度,已然成为企业巩固自身核心竞争力的关键所在.Bahrami B等[1]将订单分拣(Order Picking,OP)定义为涉及从指定的储存位置检索产品以满足客户需求的过程,并被认为是仓库中最劳动密集型的作业,约占为仓库作业成本的55%.此外虽人到货拣选系统(Pickers-to-Goods,PTG)所需的投资相当低,但缺点是拣货人员行走时间占总订单分拣时间的50%以上[2,3].

“货到人”拣选系统(Goods-to-Pickers,GTP)是为适应配送中心完成多品种、高频率、小批量的海量客户需求而提出的新模式,由储存系统、输送系统、拣选系统三部分组成.相对于传统的人到货拣选系统(Pickers-to-Goods,PTG),可有效避免拣货人员行走于货架之间的冗余时间,降低劳动强度、提高拣选效率,近些年来被广泛应用于电商、服装、医药等行业.而移动机器人履行系统(Robotic Mobile Fulfillment Systems,RMFS)是“货到人”拣选系统的主流拣选形式.该系统可根据订单波峰波谷调整移动机器人及货架的数量,使系统对拣选量变化较大的配送中心能够作出迅速的调整及重规划,这使RMFS拣选系统具备柔性强、成本低等优点,有利于提高系统的整体生产率和效率.

在GTP系统订单分批研究中,已有文献研究各种情况下的订单拣选问题[4].李珍萍等[5]建立了订单分批拣选联合优化问题的混合整数规划模型,目标是最小化货箱出库总次数.李珍萍等[6]以订单分批拣选总成本极小化为目标,给出了基于商品品项信息和货架信息的类中心的定义,提出了K-max聚类算法求解订单分批问题.陈广锋等[7]以最佳货位的最大完工时间为目标建立了数学模型,利用拉格朗日差值方法优化了差分进化算法局部搜索的能力.胡金昌等[8]以最小化料箱出入库数量为目标,来解决订单排序优化客户分批问题,提出种子算法和遗传算法进行求解,实验表明不同的方法可以依据不同的规模场景提高系统效率.万明重等[9]设计订单分批算法和智能果蝇优化算法,实验表明考虑拆分策略能够明显减小订单拣选的总延迟时间.

刘凯等[10]提出求解订单分批问题的启发式聚类算法,并设计了仿真实验将所提策略与随机分批方式进行对比.吴仁超等[11]针对订单分批问题,提出了一种混合元启发式算法,实验表明,所提分批算法在求解质量上要优于多重变邻域搜索、禁忌搜索等算法.Nicolas L等[12]以最小化总完成时间为目标构建了订单批处理模型,提出了一种元启发式方法求解模型,并将其拓展到仓库中具有多个分区的情况.Cav A等[13]以最小化拣货距离为目标建立了订单分批模型,提出了一种启发式算法求解整数规划模型.Chen等[14]提出了混合粒子群优化( PSO)和ACO算法,求解以最小化行驶总距离为目标的订单分批问题.

在处理限时订单的拣选﹑配送问题中,保障订单及时到达客户,提高客户满意度这一目标对于处理限时客户订单是至关重要的因素.只有少数学者将总延迟时间作为优化目标融入至订单分批问题中.赵金龙等[15]建立以最小化总延迟时间的整数规划模型,利用改进的智能果蝇优化算法确定订单分配和排序决策;Chen等[16]在考虑客户订单总延迟最小的情况下,提出了混合遗传和蚁群优化算法,提出的混合算法在求解质量上优于多遗传算法和到期日期优先算法.此外在上述研究中[6,7,9-14],强调了对融入启发式搜索的混合算法的性能和改进效果;因此本文结合RMFS系统的特点,提出一种融合大邻域搜索的改进差分进化算法,引入大邻域搜索的破坏、修复思想与一批基于随机、基于最大代价贡献和基于集中批次的移除算子以及新的插入算子组件,以最小化订单总延迟时间为目标对不同规模的限时客户订单分配高质量批次,提高拣选效率.

1 RMFS拣选系统

RMFS拣选系统由调度系统、移动机器人、拣选台、拣货员、可移动货架、巷道和充电站组成,整体布局如图1所示.RMFS拣选系统订单拣选作业流程如下:(1)系统依据库存信息以及任务信息对已接收的订单分配给目标货架及拣选台;(2)系统确定需要执行的机器人,并判断机器人自身电量是否有足够的时间移动至目标货架,若有则由该机器人执行拣货任务,若无则需前往充电区域充电,直至电量达到20%后继续完成任务;(3)移动机器人按照规划好的最优拣选路径移动至目标货架;(4)到达目标货架后,移动机器人顶升、抬起可移动货架并将其运送至目标拣选台;(5)到达拣选台后,按照如图2所示进行排队拣选,直至拣货员开始执行该任务;(6)待拣货员拣货完成后向系统进行反馈,系统规划好移动机器人的路径,命令其将货架放回存储区;(7)移动机器人将货架放回存储区,即完成当前任务的拣选,系统将释放移动机器人并命令其返回待命位置;(8)若移动机器人任务密集时,则需就地待命,若否,移动机器人需返回停车区.拣选流程如图3所示.

图2 RMFS系统中的拣选台

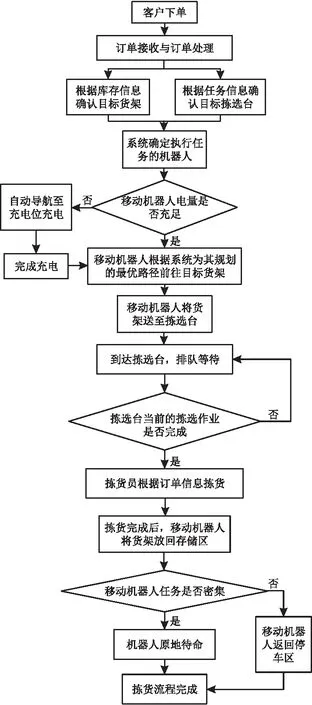
图3 RMFS系统订单拣选流程

在RMFS拣选系统中,往往同一批次的订单需要移动机器人多次搬运以及拣货员在可移动货架上多次拣选才能完成.而传统的订单分批方法比如随机分批或低质量的订单分配批次会使得移动机器人和拣货员频繁操作,从而增加设备及人力损耗,同时也会使移动机器人进行多次运输作业增加订单拣选时间、降低拣选效率.为解决这一难题,本文首先针对RMFS拣选系统,建立以最小化订单总延迟时间为目标的订单分批优化模型,提出了融合大邻域搜索的改进差分进化算法,引入移除、插入算子组件,优化客户订单分配,构造高质量批次,避免设备损耗,减少订单拣选时间及资源闲置,从而提高客户满意度及仓库拣选效率.

2 订单分批优化模型

2.1 条件与假设

本文所有假设如下:

(1)同一订单的SKU不能拆分为不同批次.

(2)任何单个存储位置都有足够的SKU用于批量订单,不会出现缺货现象.

(3)同一批次中不同订单的同一SKU是从同一可移动货架上拣选的.

(4)可移动货架上的存储SKU的货位固定、货架位置固定.

(5)若两个订单中包含同一SKU,将其合并拣选能减少拣货员拣选操作一次的时间.

(6)若两个订单中包含的SKU位于同一货架,将其合并拣选可以减少一次移动机器人搬运的时间.

(7)已知移动机器人每搬运一次货架的时间简化为t1及拣货员拣选一次SKU的时间为t2.

(8)同一移动机器人,单周期内仅需处理某一批次订单,且必须完成当前周期的当前批次所有拣选任务后,方可开启下一周期内某一批次的拣选任务.

2.2 模型建立

假设系统某一时刻的订单池中,共有N张具有不同截止时间的订单O1,O2,O3,…,Oi等待处理,每条订单有M种SKU且货位信息已知,用aim=1表示订单i中包含商品m,否则aim=0,此外每个可移动货架s1,s2,s3,…se上可摆放5种SKU,用bme=1表示商品m在货架e上,否则bme=0.同时设置移动机器人搬运一次货架的时间t1及拣货员拣选一次SKU的时间t2.其次考虑到电商行业订单需要快速响应,从而保障订单及时到达客户这一现状,本文定义了订单i的延迟时间为订单结束时间与截止时间差,如式(1)所示:

(1)

(2)

(3)

综合考虑以上的订单延迟时间、拣选时间和批次容量约束,可建立以最小化订单总延迟时间为目标的订单分批优化模型.

(4)

s.t.

(5)

(6)

(7)

(8)

(9)

(10)

xij∈{0,1},∀i∈I,j∈J

(11)

yje∈{0,1},∀j∈J,e∈E

(12)

zjm∈{0,1},∀j∈J,m∈M

(13)

目标函数(4)表示以最小化订单总延迟时间;式(5)表示每个订单只能被分到一个批次;式(6)表示批次j中任意订单i中包含商品m,则批次j包含商品m;式(7)表示如果批次j中包含商品m,则移动机器人需要搬运商品m所在的货架e,其中yje为0-1变量,若拣选批次j需要搬运货架e,则yje=1,否则yje=0;式(8)表示批次j的完成拣选的时间,为批次j开始拣选的时间与批次j的服务时间的和;式(9)表示批次j的开始时间,为该批次内订单i的最早到达时间;式(10)表示批次j的服务时间,为移动机器人搬运货架的时间与拣货员的拣货时间和;式(11)至式(13)表示决策变量取值约束.

3 一种融合大邻域搜索的改进差分进化算法设计

差分进化算法(Differential Evolution,DE)是从仿生智能计算(Bionic Intelligent Computing,BIC)出现以来,优化算法结构中的又一大进步,其保留了一对一的竞争策略和基于种群的搜索方式[17].由于该算法具有优越的全局收敛能力,求解过程和方法较为简单等优点,因此DE算法更适用于求解较为复杂的大规模全局问题.但是传统DE算法因其单一的变异策略、固定不变的邻域值和缓慢的静态邻域拓扑交换速率,导致其全局与局部之间的搜索能力无法达到均衡等问题.而大邻域搜索算法(Large Neighborhood Search,LNS)可通过一组移除和插入算子进行动态邻域搜索,使算法具备了良好的适应能力[18].同时移除算子和插入算子能够针对问题特性灵活设计,可扩展度高.本文在传统DE算法的基础上融入大邻域搜索算法(Large Neighborhood Search,LNS),设计了3个移除算子和2个插入算子,提出了应用于RMFS系统离散型订单分批问题的融合大邻域搜索的改进差分进化算法.

3.1 移除算子

(1)基于随机的移除算子:从当前解中随机移除批次Bj中的ni笔订单.

(2)基于最大代价贡献的移除算子:优先移除延迟时间代价贡献最大的批次Bj中的订单Oi.某个订单Oi的代价贡献由式(2)计算,采用轮盘赌的方式,从当前解中选择ni笔订单进行移除操作,定义订单Oi的权重Qi=τi.

(3)基于集中批次的移除算子:集中移除一个批次上的订单.从当前解中找到某个代价最大的批次,随机移除该批次上的所有订单.若无符合条件的批次,则退化为随机移除算子.

随机移除算子为纯随机算子,具有随机性强、跳出局部最优的能力较强的优点,但也容易移除在正确位置上的订单,从而产生无效操作;最大代价贡献移除算子会将延迟时间贡献最大的订单优先考虑,而这些订单往往正是需要优化的订单,缺点是容易陷入局部最优;集中批次移除算子会集中移除一个批次上的所有订单,策略简单且具有良好的局部收敛能力,这两种移除算子均需要遍历一遍当前解中各个订单的属性,故以上三种移除算子的时间复杂度分别为O(1)、O(n)、O(n).

3.2 插入算子

(1)贪婪顺序插入算子:每个订单i由贪婪策略得到插入位置,也就是选择使本次插入增加的总延迟时间最小的位置插入,将待插入订单随机乱序后依次贪婪插入.

(2)遍历插入算子:随机选择两个移除的订单,将其它订单顺序打乱后依次以贪婪法插入,然后选择两个订单中的第一个订单,分别固定到使延迟时间增加最小的前[ky×n]个批次中.对另一订单遍历所有批次即位置,以概率p直接选择其中最优的邻域解,但仍有1-p的概率以赌盘方式选择一个邻域解,每个邻域解的权重为其适应值.其中ky为(0,1)之间的常数.

根据待插入订单需要尝试的批次数和,贪婪顺序插入算子与遍历插入算子的时间复杂度均为O(n),是算法的主要耗时部分之一.因移除算子的时间复杂度均小于O(n2),故每次选择一个移除算子和一个插入算子执行的时间复杂度仍为O(n2).此外贪婪顺序插入算子存在易陷入局部最优的缺点,而遍历插入算子在很大程度上弥补了这种局限.

3.3 LNS_DE算法步骤

本文提出的LNS_DE算法进行优化的步骤如下,算法流程图如图4所示.

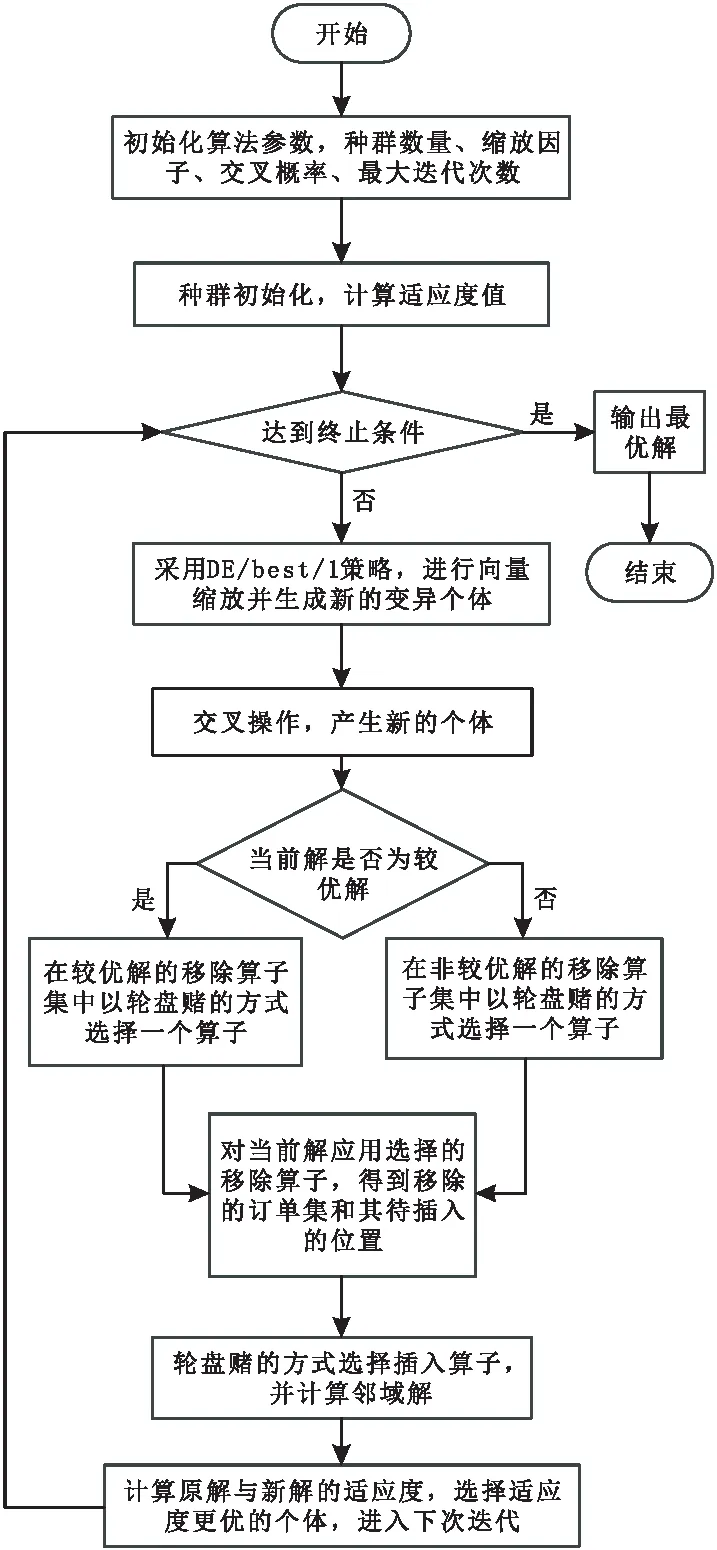
图4 LNS_DE算法流程图

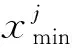
(14)

并设定算法相关参数,包括种群数量NP、缩放因子F、交叉概率CR、最大迭代次数genmax等参数.

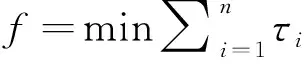
(3)记录当前个体最优值以及全局最优值.

(4)经过步骤(3)后进入迭代循环,当迭代循环小于次数genmax,执行如下操作:

①变异

针对每个个体向量,执行差分变异操作会产生变异向量.在DE中共有常用的5种变异策略产生变异个体Vi,G,以DE/best/1策略进行变异操作,如下所示:

Vi,G=xbest,G+F(xr1,G-xr2,G)

(15)

式(15)中:xrm,G是m=[1,2,3,…,M]中随机选择的不同的个体,与目标个体xi,G不相同;xbest,G是种群中适应度最好的个体;缩放因子F是[0,2]中的一个实常数因数,起到对控制偏差变量的放大作用.

②交叉

在变异操作后,需将目标向量xi,G与变异向量Vi,G进行二项式交叉生成最终的试验向量Ui,G=[Ui1,G,Ui2,G,…,UiM,G],依下式进行交叉操作,以增加干扰参数向量的多样性:

(16)

式(16)中:jrand是集合{1,2,…,M}内随机选择的一个整数,以保证变异向量至少有一维信息被保留下来;交叉概率CR是区间[0,1]之间的常数.

③判断当前解是否为较优解,若是,则在较优解的移除算子集中以轮盘赌的方式选择一个算子;若不是,则在非较优解的移除算子集中以轮盘赌的方式选择一个算子;

④对当前解应用选择的移除算子,得到移除的订单集和其待插入的位置,以轮盘赌的方式选择插入算子,并计算邻域解;

⑤计算原解与新解的适应度;

⑥选择适应度更优的个体,转至步骤①进入下一次迭代循环.

(5)当迭代次数等于genmax时,迭代停止,并输出最终的全局最优值.

4 数值算例

4.1 参数校准

该算法框架主要有3个参数,为每种算例类型寻找最佳参数设置非常耗时.相反,更希望在广泛的算例类型上提供良好结果的参数设置.因此,必须校准所涉及的3个参数.本研究基于Coy等[19]中提出的系统参数校准过程,为这些问题算例查找高质量的参数设置.因此整个参数设计实验包括四个步骤:选择问题子集,确定每个参数变化的设计中心和范围,组合参数设置并进行算例验证,最后确定每个问题集良好的参数设置.

在参数校准中,选择代表整个问题集特征的3个不同算例作为实验子集.确定实验子集后,依据各参数本身的性质设置设计中心和变化区域,如表1所示.最小值和最大值代表实验区域的外边缘,根据步长可计算参数的不同水平值.

表1 参数校准初始实验区域

由于必须校准3个参数,利用田口方法论为3个因子和4个水平进行析因设计,以确定实验结果稳定、波动性小的参数组合[20,21].如表2所示,从正交表中选择L16正交阵列,对于16种配置中的每种配置,在算例类型为50个订单、10个货架上执行5次运行以获得算法最优解平均值Abs_Obj.并通过方差分析法可以找到重要参数,从表2可以看出,对于算例1来说因子F(缩放因子)对算法的影响最大,其次是因子NP(种群规模),因子CR(交叉概率)对算法的影响最小.算例1中每个因子的最佳水平为NP3、F4和CR4.

表2 正交表及方差分析

接下来,为每个算例选择最优解平均值最低的参数设置.结果设置如表3所示,通过取实验子集的参数设置的平均值,可以获得最终参数设置,该参数设置将用于进一步的实验,并在广泛的问题类型上可提供高质量的解决方案,以显示所提出的算法框架的计算性能.

表3 参数校准结果

4.2 实验结果

上述研究的参数设置用于下面讨论的所有实验.第一部分实验在基于每个算例类型上比较使用DE算法、LNS_DE算法,每组实验分别重复10次,累计2x6x10=120组试验.并统计了两种订单分批算法的最优解平均值Abs_Obj、平均偏差值Dev、平均目标值优化比例MPI及平均运行时间T.其中Dev表示在一类算例中,当前算法最优解平均值Abs_Obj与已知最优解之间的平均百分比偏差值,已知最优解是DE、LNS_DE中发现的最优解的平均值;MPI表示LNS_DE求解结果对比DE的改进程度.

表4比较了在6个算例类型中,DE算法、LNS_DE算法的性能.在求解质量上,LNS_DE算法在所有算例类型上均优于DE算法.具体表现为,所有算例上,LNS_DE算法解的平均值优化比例随着订单数量的增大而增大,优势在不断扩大,平均缩短了22.05%的延迟时间,在N/E/M=300/50/250时最大可减少71.6%的延迟时间.此外LNS_DE算法平均偏差值Dev小于DE算法,这表示在每个算例类型中,LNS_DE算法都发现了最多的已知最优解,尤其在N=75后平均偏差值Dev均为0,说明每次实验已知最优解全部来源于LNS_DE算法;在求解时间上,LNS_DE算法并未优于DE算法,但计算时间差率大小控制在合理范围内:2%～7%,这是由于任何混合算法性能的提高都是以牺牲算法搜索时间为代价;且随着客户订单数量增大时,两种算法执行时间均呈一定幅度下降.

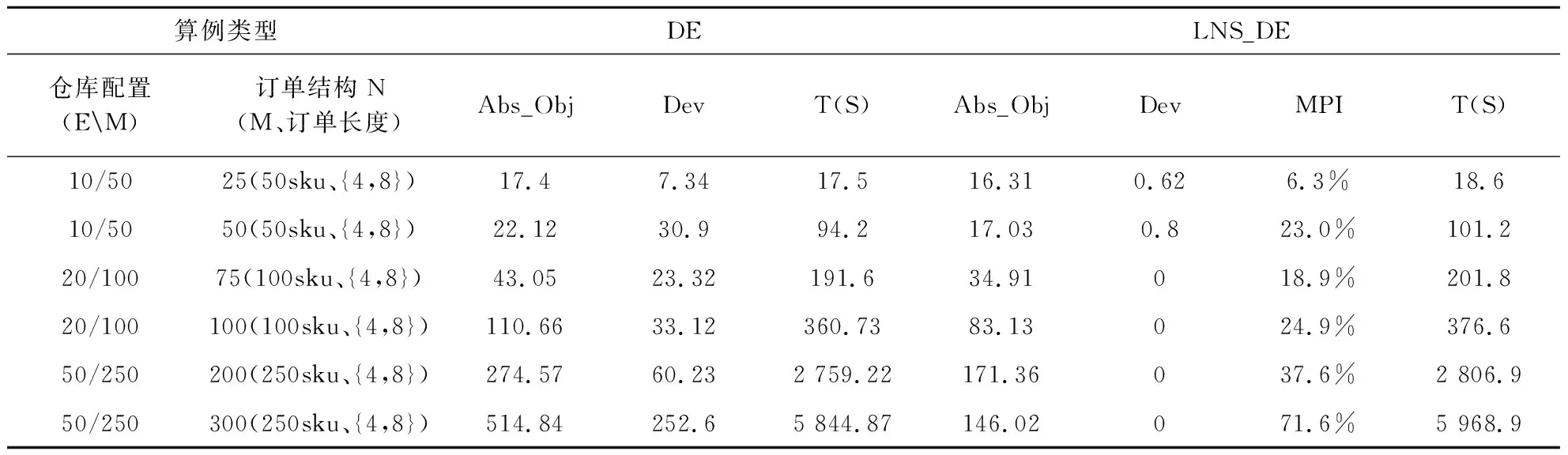
表4 两种分批算法在不同算例中的计算结果

企业促销活动时,客户反映表现为两方面,一方面是购买订单增加带来的订单行增加,另一方面是客户一起购买的商品增加,即订单长度增加.因此第二部分实验探究订单长度对分批效果的影响.基于算例类型N/E/M=100/20/100,在不同的订单长度({1,4}、{1,6}、{1,8})上统计了LNS_DE算法和DE算法的订单总延迟时间,累计2×3×10=60组试验.

图5呈现了DE算法、LNS_DE算法在3种订单长度下的订单总延迟时间数值.虽然随着单个订单所包含的的商品种类扩增时,两种算法所求解的订单延迟时间均进一步延长,但延迟时间也在合理范围之内.另外LNS_DE算法分批效果明显优于DE,且在订单行长度为{1,8}时,优化效果达到最大,说明在订单分批流程时,管理者可选择LNS_DE算法缓解延迟时间所带来的经济损失,得出的方案对企业面临大型促销活动时,可实现快速响应客户这一点.

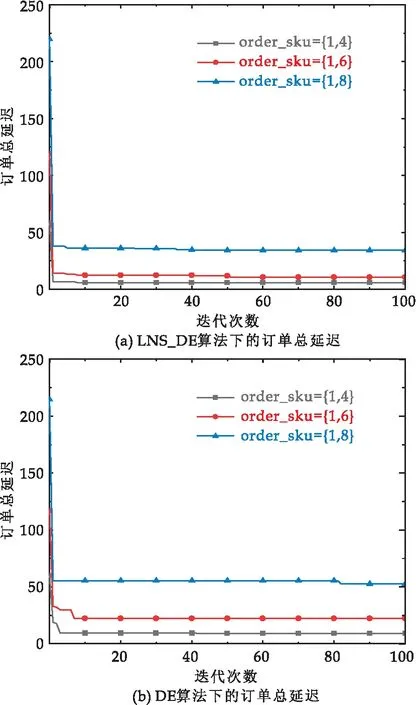
图5 两种算法在不同订单长度下的总延迟时间

图6记录了DE算法、LNS_DE算法在不同规模算例下的计算迭代过程.可以发现DE算法的收敛速度较快,但易陷入局部最优,而本文所提出的LNS_DE算法通过扩大邻域搜索范围,能够有效提高算法精度;同样LNS_DE算法得到的最优解适应度值均优于DE算法,且随着订单规模的增大,适应度值的优化效果愈加明显.

5 结论

(1)以最小化订单总延迟时间为目标,建立基于“RMFS”拣选系统的订单分批优化模型.

(2)引入大邻域搜索的破坏与修复思想及一批基于随机、基于最大代价贡献和基于集中批次的移除算子以及新的插入算子组件,设计出融合大邻域搜索的改进差分进化算法对模型进行求解.

(3)对于不同规模的限时客户订单结构,LNS_DE算法通过扩大邻域搜索范围,能够有效提高算法精度,平均缩短22.05%的延迟时间,与差分进化算法(DE)相比,求解质量更优、性能更稳定、收敛速度更快.

(4)面对大型促销活动所带来的订单长度增加、高订单数量时,本文算法解的优化比例不断扩大,主要体现在LNS_DE算法平均偏差值Dev均小于DE算法,且在N=75后均为0,说明每次实验已知最优解全部来源于LNS_DE算法,故该方法所求解高质量的订单批次可有效缩短拣选时间,提高拣选效率.

(5)此外,LNS_DE算法与DE算法计算时间差率大小始终保持在合理范围内:2%～7%.