不同雨型下城市雨洪模拟效果分析

季 平，王祥静，万 颖

(四川北极星水利工程设计有限公司，四川 绵阳 621000)

在全球变暖和城市化进程快速发展的大背景下，世界范围内极端降水事件增加，由此导致的城市内涝灾害也愈发频繁[1]。截至2020年末，我国城镇化率已超过60%[2]，城市化建设改变了城市区域下垫面特征，不透水路面的增加对降水径流关系产生了显著影响，导致径流量加大，洪涝风险也随之增加[3]。近10a间，我国遭受洪涝灾害的城市超过80座，受影响人口超过5000万，直接经济损失达千亿以上[4]。如2012年7月，北京及其周边地区遭遇60a一遇极端强降水，受灾人口约160万，经济损失达116.4亿元[5]；2020年长江流域遭遇持续性强降水，重庆、四川、安徽、江西等27个省(区、市)受灾，造成直接经济损失约700亿元[6]。城市地区由于人口和财产集中，在遭遇同等规模暴雨下所造成的洪涝损失往往更大[7]，城市洪涝灾害已经严重威胁到经济社会的可持续发展与人民的人身财产安全[8]。

降水是引发洪涝事件的直接驱动因素，近年来，众多学者针对降水过程对城市洪涝展开了研究。如：曾鹏等[9]利用IFMS模拟了成都市中心城区在不同重现期及不同降水历时下的内涝积水情况，并进行风险等级划分；张金萍等[10]模拟了郑州市金水区城市排水管网在极端暴雨情景下的排水能力和内涝积水特征；李智等[11]利用SWMM模拟技术模拟了涂家营沟流域内不同子汇水区域在不同重现期降水下的淹没情况，并识别出洪灾危险区；黄国如等[12]基于芝加哥雨型设计了不同重现期下的降水过程，并模拟了海口地区在不同设计暴雨情景下的洪涝过程；Ng等[13]基于Huff雨型对不同强度、历时的降水过程进行模拟，并对城市排水系统进行敏感性分析，认为拓展排水管网规模是降低内涝程度的有效手段；Li等[14]模拟了不同重现期降水过程下的城市径流过程，并对海绵城市LID设施的消峰减洪效益进行评价。以上研究表明，不同强度的降水和降水过程下城市径流的形成过程存在差异，分析城市径流对降水模式的响应特点，对揭示城市洪涝灾害致灾机理、完善城市洪涝预警系统、提高城市防洪减灾能力具有重要意义。因此，本文拟以绵阳市为研究区域，结合典型降水过程和芝加哥雨型方法，比较不同重现期下设计暴雨过程与实际暴雨事件的差异；利用SWMM模型对不同暴雨情景下的城市径流过程进行模拟，分析径流特征值对不同设计暴雨过程的响应特点，以期为区域城市洪涝灾害预警、防洪减灾工作部署提供参考。

1 研究区及数据

绵阳市位于中国四川盆地西北部，涪江中上游区域，该区域地处亚热带山地湿润季风气候区，夏季炎热多雨，短期强降水频繁[15]。绵阳市属涪江流域，流域中上游雨量充沛，主汛期集中在6—9月，径流量年际变化较大[16]。绵阳市位于涪江流域中上游，近年来由于城市化进程加快，河道变窄，城市洪涝灾害愈发频繁[14]。本研究中2015—2020年小时降水数据来自涪江桥水文站，区域地理特征参数(面积、坡度、形状等)和土地利用数据来自于ASTER-GDEM和Globeland 30数据集，主要用于典型暴雨过程的筛选和模型输入；2000—2020年小时径流数据来自安昌、芙蓉溪、丰谷、涪江桥4个水文站，用于模型参数验证。

2 研究方法

2.1 芝加哥雨型

芝加哥雨型法是一种非均匀设计雨型，是在暴雨强度公式的基础上，根据雨峰位置系数推求指定历时与重现期下的降水过程[17]。暴雨强度公式为：

(1)

式中，q—降水强度，mm/min；A—重现期为1a的设计降水量，mm；C—雨量变动参数，无量纲；P—重现期，a；b—降水历时修正参数，min；t—暴雨历时，min；n—暴雨衰减指数，与重现期有关，无量纲。

雨峰位置系数可以体现降水峰现时间与总历时的比值，表达式为[18]：

(2)

式中，r—雨峰位置系数；t—降水峰值出现的时刻；T—降水历时。

降水过程峰前、峰后瞬时暴雨强度的表达式分别为[19]：

(3)

(4)

式中，qa—降水峰前瞬时暴雨强度；qb—降水峰后瞬时暴雨强度；ta—峰前降水历时，min；tb—峰后降水历时，min；a、b、c—常数，a=167A(1+ClogP)，b与c共同反映降水强度随时间变化递减情况。

2.2 雨洪管理模型

由于城市区域观测条件限制，目前关于城市雨洪研究多采用模型模拟的方法[20]。SWMM是由美国环保署开发的基于水动力学理论的城市雨洪模型，能够模拟降雨径流转化过程，在城市暴雨洪水模拟方面应用广泛[21]。本研究中下渗量的计算采用Horton公式，计算公式如下[22]：

fp=f∞+(f0-f∞)e-kt

(5)

式中，fp—土壤下渗率，mm/h；f0—初始下渗率，mm/h；f∞—稳定下渗率，mm/h；k—下渗衰减系数，1/h；t—下渗历时，h。

地表汇流过程按照非线性水库模型计算，非线性水库模型中的连续方程表达式如下[23]：

(6)

式中，V—表面径流体积，m3；t—降水历时，s；A—子汇水区面积，m2；d—子汇水区地表水深，mm；i—降水强度，mm/s；Q0—径流流量，m3/s。

径流量的计算采用曼宁方程，计算公式如下[24]：

(7)

式中，n—曼宁粗糙系数；W—宽度特征，m；dp—滞蓄水深，m；S—子汇水区域地表坡度。

3 结果与讨论

3.1 模型验证

为使模型在模拟不同降水情景下都有足够适用性，选择实测降水事件进行模型可靠性验证。由于绵阳市城区无水文站观测数据，结合上下游水文站点观测数据，利用水量平衡方程估算出研究区域最大年径流流量(189.6m3/s，7月)作为实际径流流量。SWMM模型参数取值参考SWMM用户手册及相关文献[4，14，24]，对较为敏感的洼地蓄积量参数和渗透参数进行进一步调整，利用校准后的模型对绵阳市中心城区2010年8月19日的雨洪事件事件进行模拟，模拟流量结果为164.9m3/s，模拟值与实测值误差约13%，表明模型参数校准结果符合模拟要求，可用于研究区域雨洪过程模拟。

3.2 暴雨过程设计

为研究不用雨型下绵阳市的雨洪响应过程，本研究选取2015—2020年间汛期内(6—9月)各月最大降水量对应的暴雨事件作为典型暴雨过程(主要为单峰型)；基于典型暴雨过程通过设置雨峰位置系数r，获得不同雨峰出现时间的设计雨型，设计雨型分组与重现期设置情况见表1。

2015—2020年汛期期间6—9月典型暴雨事件和芝加哥雨型暴雨过程如图1所示。

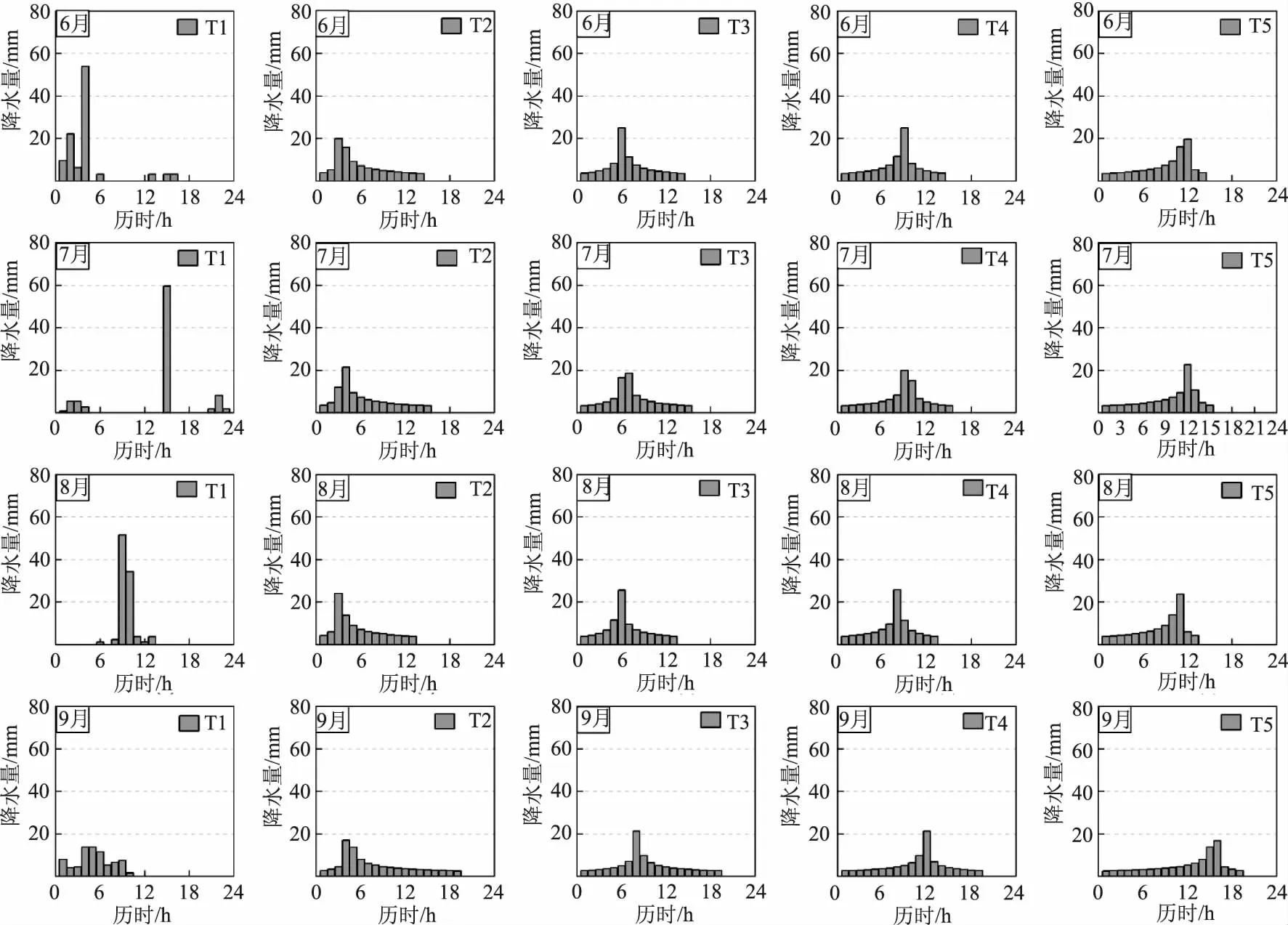
图1 典型暴雨与芝加哥雨型设计暴雨过程对比

结果显示，6和8月的典型暴雨过程呈单峰形态且峰值明显，7月的降水过程更为集中且峰值更高，最大雨强为59.58mm/h，最大日降水量超过98mm，峰值雨量占总雨量比重约69%；9月的暴雨降水过程峰值不明显，小时降水量均低于15mm，总降水量也较其他月份低，为77.38mm，峰值雨量占比仅18%。

芝加哥雨型均为单峰降水过程，峰值两侧降水变化过程基本对称，峰值出现时段取决于雨峰位置系数r，r值越大，雨峰位置越靠后。相较于典型暴雨事件，同降水总量的芝加哥雨型的降水过程更连续，单位时段降水量多低于15mm，峰值雨量占比在20%～25%之间，降水过程起伏缓慢且历时较长；峰现时间靠前(r=0.2)的芝加哥雨型与6、9月的典型降水过程拟合程度更高，相关系数分别为0.57和0.85；峰现时间靠后(r=0.8)的芝加哥雨型更贴合8月的典型暴雨过程，相关系数为0.44。

3.3 不同雨型下的城市雨洪响应分析

为分析绵阳市在不同降水过程下的城市径流情况，分别输入不同月份(6、7、8、9月)、不同雨型(T1、T2、T3、T4、T5)、不同重现期(2、5、10、20、50、100a)共120种设计暴雨情景，利用SWMM模拟得到各暴雨情景下的径流过程，具体结果如图2所示，见表2。

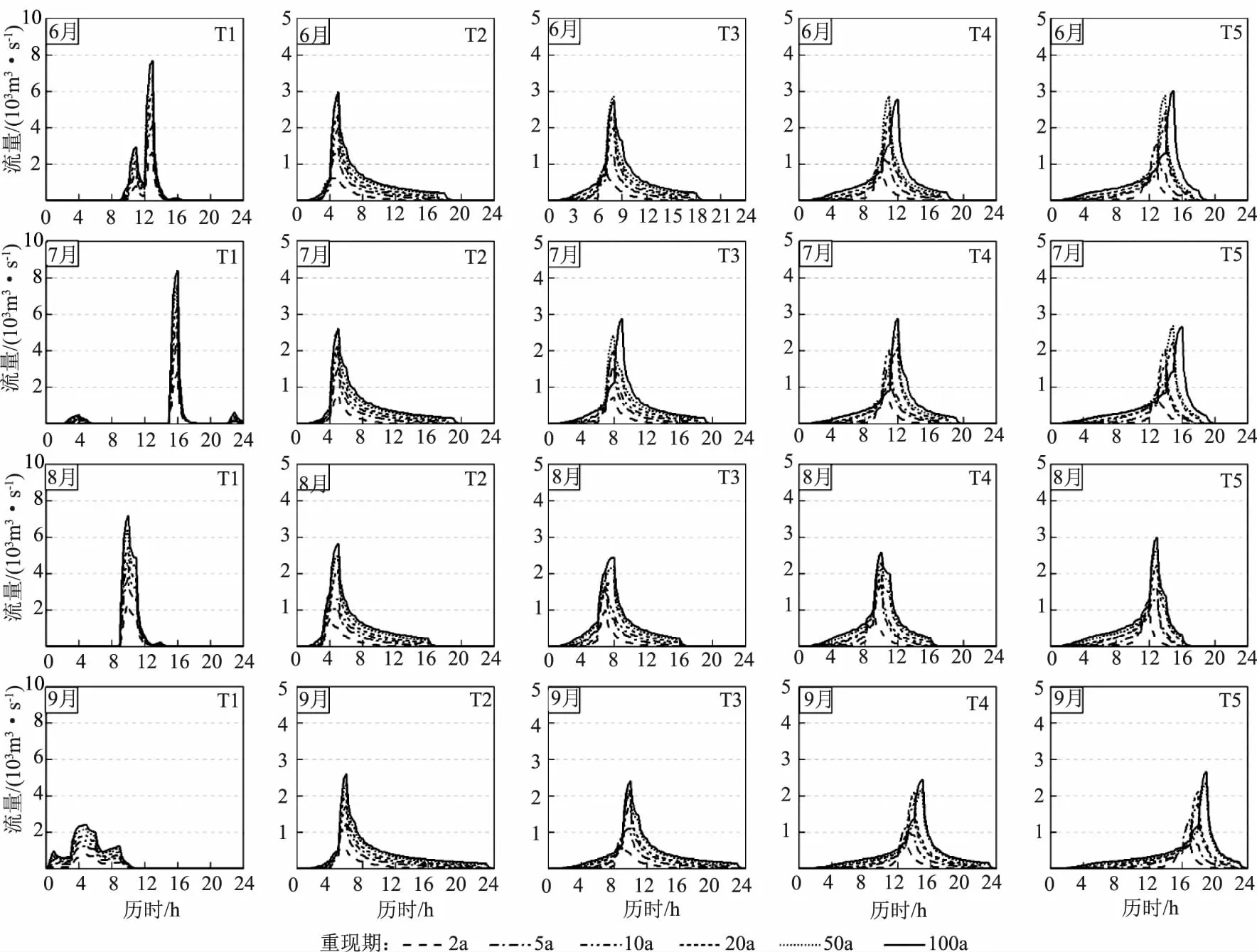
图2 不同重现期下典型暴雨与芝加哥雨型下径流过程对比

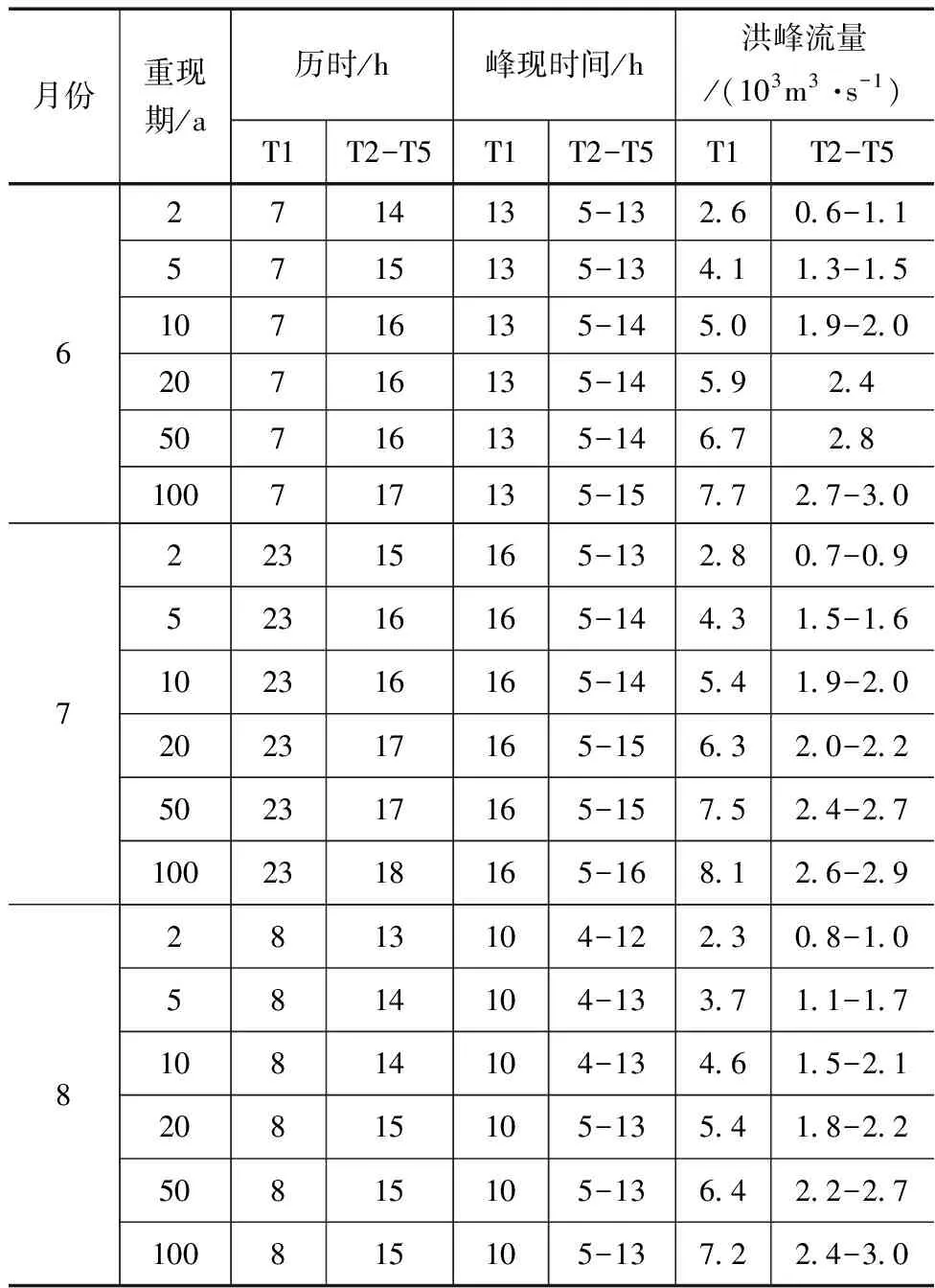
表2 绵阳市不同重现期下各雨型径流过程模拟结果

在洪水历时方面，集中强降水产生的洪水径流过程持续时间更长，如7月典型暴雨(T1)产生的洪水历时为23h，其他月份均低于10h；芝加哥雨型下(T2-T5)的洪水过程历时较为均匀，在13～22h范围。各雨型在不同重现期下产生的洪峰流量具有较大差异，6—8月期间芝加哥雨型下的洪峰流量均低于历史暴雨事件产生的洪峰流量，9月各雨型的洪峰流量接近；雨峰出现较早(T2)和较晚(T5)的雨型生产的洪峰流量较大，如8月T2、T5雨型下重现期为100a的洪峰流量分别为2.8和3.0，103m3/s，而T3、T4雨型下的洪峰流量仅为2.4和2.5，103m3/s，其他月份也有类似情况。关于峰现时间，雨峰靠后的雨型(T5)产生的洪峰，其出现时间随重现期的增加向后推移，如T5雨型下100a一遇洪水的洪峰出现时间比2a一遇洪水的晚2h，而雨峰靠前的雨型(T1)则无此现象。芝加哥雨型下的洪峰流量低于实际洪峰流量，如6—8月间芝加哥雨型下5～20a一遇的洪峰流量比相同重现期下实际暴雨事件产生的洪峰流量值低50%以上。

4 结论

本文以绵阳市城区作为研究区域，基于水文站降水、径流数据，结合芝加哥雨型和SWMM模拟，探讨了不同时期、不同峰现时间暴雨作用下绵阳市的雨洪响应特征，得到结论如下。

(1)雨峰出现较早(T2)和较晚(T5)的单峰型暴雨可能产生的洪峰流量更大。

(2)在高强度暴雨下(重现期>50a)，雨峰靠后的雨型(r≥0.6)可能产生的洪峰流量更大且峰现时间随重现期增加而推迟。

(3)芝加哥雨型下的洪峰流量普遍低于实际暴雨过程可能形成的洪峰流量，尤其对短历时高强度降水过程。

研究结果对揭示城市雨洪响应过程具有重要意义，但雨型设置略显单一，在今后的研究中，可增加多峰雨型模拟情景，以获得更可靠、科学的评估结果，为完善城市洪涝灾害预警系统建设、提高城市洪涝风险管理水平提供理论依据。