基于PSO-LSTM神经网络的沙坪水电站水位预报方法研究

韩利国

(阳泉市水文水资源勘测站，山西 阳泉 045007)

径流式水电站广泛存在于梯级水库中。其来水和水位预报受诸多水力和机组特性控制因素影响，变化趋势具有较强的非线性和随机性，难以用传统水动力模型准确模拟。水位高精度预报问题已成为制约水电站精细化运行的一大障碍[1-2]。近年来，国内外对水电站来水预报及其不确定性进行了大量研究。文献[3]采用基于混沌理论的局部逼近模型对丹江口水库月径流量进行了预测。模型结果达到了较高的精度。纪昌明等[4]基于梯级水电站安全运行预警机制建立梯级水电站负荷调整耦合模型，旨在解决因来水不确定性导致实际调度要求与原发电计划偏差的问题。同时解决了电站被迫减少出力运行或因来水不确定性导致水库弃水的问题。

随着人工智能的发展，神经网络以其强大的非线性能力和数据驱动被学者们用于径流预报[5-6]。纪昌明等[7]基于小波分解的投影寻踪建立自回归组合预测模型预报宜昌站年径流量。朱双等[8]采用基于灰色关联分析的模糊支持向量机方法对金沙江上游石鼓站月径流量进行了预测，取得了较高的预测精度。唐明等[5]采用LSTM模型对南水北调中线工程进行了水位预测。同时分析了模型参数对预测精度的影响。

而梯级水库群系统不仅具有经济效益和防洪功能，内部成员之间还具有关联性和补偿性。因此，在单水库水位预测中需要考虑上下游水库径流的水力联系以及二者之间水位差形成的电气联系[2]。目前，大多数预测方法都采用长序列的实测数据进行数据建模。这种方法受地形和相关水电站运行情况的影响。一些径流式水电站的实测数据是不断变化的。它们预测时间短，数据样本少，波动大，导致实际建模中存在很多问题[1，9，10]。

沙坪水电站受流域地形、上游出水量和发电计划的影响。这导致了水位预测的困难和频繁的闸门移动[10]。本文采用PSO-LSTM神经网络构建沙坪水电站水位预测模型，采用上游枕头坝出库流量、沙坪过往运行数据、未来发电计划和闸门开度作为模型参数。与传统的水平衡模型相比，模型的精度有了很大的提高。利用该模型实现了沙坪水电站水位的快速预报，同时减少了闸门操作次数。这些结果为径流式水电站的水位预报和精细化管理提供了参考和借鉴。

1 研究区域和数据

本文以大渡河规划的梯级水电站之一的沙坪水电站为研究对象。位于四川省乐山市峨边彝族自治县、金口河区境内的大渡河干流段。与下面的沙坪一级水电站、龚嘴水电站相邻。沙坪二级水库总库容2084万m3，运行水位范围550.0～554.0m。因为550m为水库死水位，554m为正常蓄水位。4m水位运行范围内库容仅585万m3。其结果是水库库容小，水位可调范围有限。因此，水库水位对上游流量的变化十分敏感，难以准确预测。以沙坪水电站2019年1月1日—12月31日间隔5min的实测数据为研究对象。这些数据集按月的顺序分为训练集和测试集。

2 水量平衡模型

基于沙坪水电站的固有属性曲线，包括水位库容曲线、机组N-H-Q曲线、尾水位流量关系曲线等，根据水量平衡原理进行了计算。计算的前提是知道水库当前时刻坝前水位以及未来一段时间的入库流量和计划负荷。具体流程如下。

根据水量平衡公式，库容变化量等于t～(t+1)时期水电站入库水量与出库水量之差。这意味着水的总量始终保持不变。计算公式为：

(1)

3 研究方法

3.1 长短记忆神经网络(LSTM)

LSTM网络作为一种时间循环神经网络(RNN)的变种网络，LSTM添加遗忘门来解决RNN网络存在的梯度消失的问题[13-14]，实现了时间序列数据的长期预测，是当前业界应用最成功的RNN网络架构。LSTM网络拓扑如图1所示。

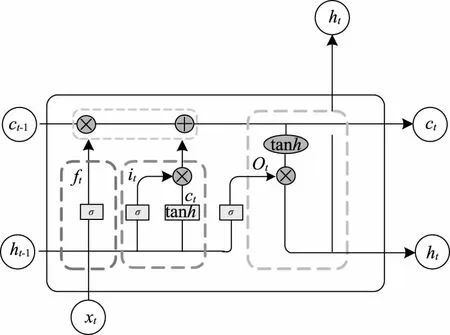
图1 LSTM网络结构图

LSTM的结构单元由红色的遗忘门、蓝色的输入门和绿色的输出门组成[17]。遗忘门ft决定信息的去留。输入门it用于更新细胞状态xt，由xt和ht-1经由sigmoid计算获得。输出门ot用来确定下一时刻状态信息的值xt+1，隐藏状态包含了先前输入的信息。首先，sigmoid函数的输入为前一时刻隐藏状态ht-1和当前输入，sigmoid传递状态信息给tanh函数，并通过激活函数tanh和sigmoid函数的输出数据相乘，确定ht携带的数据并作为输出传递给下一个时间步长。LSTM计算公式如下。

it=σ(Wi·ht-1+Wi·xt+bi)

(2)

ot=σ(Wo·ht-1+Wo·xt+bo)

(3)

ft=σ(Wf·ht-1+Wf·xt+bf)

(4)

式中，it—输入门的计算结果；ot—输出门的计算结果；ft—遗忘门的计算结果；Wi—输入门的权重；Wo—输出门的权重；、Wf—遗忘门的权重；bi—输入门的偏执项；、bo—输出门的偏执项；bf—遗忘门的偏执项；σ—激活函数。

gt=∅[Wc·(ht-1，xt)+bc]

(5)

St=ft·ct-1+it·gt

(6)

ht=ot·∅(St)

(7)

式中，gt—记忆单元输入节点；St—状态单元的状态；∅—tanh函数；Wc—输入的权重矩阵；bc—输入状态偏执项。

3.2 粒子群算法

粒子群算法(PSO)诞生于对鸟类动物种群觅食生物行为和群体行为的二维空间模拟。首先在二维空间设置了许多具有随机位置和速度的初始搜索粒子，粒子在空间通过将速度与位置相加来引导一个最佳点，完成局部寻优和全局寻优[15-16]。在寻优过程中，通过不断的跟踪最优解和对比局部搜索寻找出的最佳位置，更新整个粒子群的最优位置并保存，最终实现局部寻优到全体寻优过程的实现。PSO优化算法理论简单，易实现应用，广泛应用于最优寻解参数的自整定寻优[19]。PSO算法的公式如下。

(8)

(9)

(10)

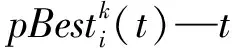
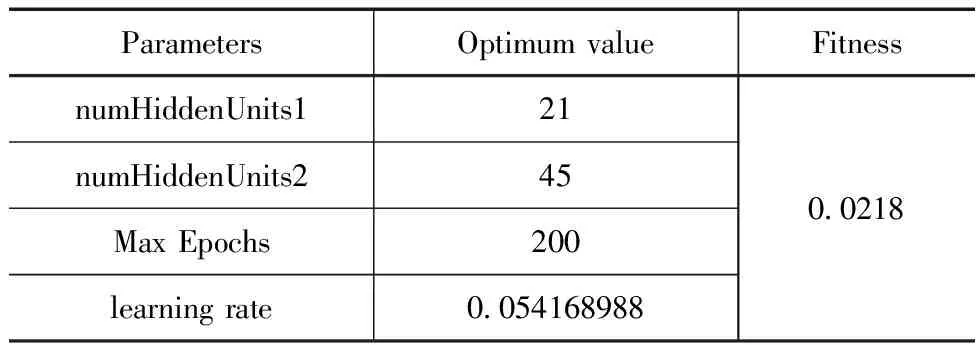
表1 PSO优化的LSTM超参数

3.3 预测性能评价指标

预测误差是预测值与预测对象的真实值之间的偏差，反映了预测算法的精确度。本文选用纳什效率系数(Nash-Sutcliffe efficiency coefficient，NSE)和均方根误差(Root Mean Square Error，RMSE)作为预测模型性能评价指标，计算公式如下。

(11)

(12)

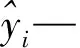
4 融合预测模型构建与训练

本文在MATLAB开发环境中完成融合预测模型的搭建和训练。本文利用PSO算法进行LSTM网络模型的参数自动寻优，以提高LSTM模型自动化程度和预测准确度。本文提出的PSO-LSTM的数据融合预测模型的预测流程如图2所示。

具体计算步骤如下。

(1)数据预处理。将数据集进行数据归一化，划分训练集和测试集。

输入数据归一化：将输入数据的取值转换映射到制定区域，以便进一步分析数据数据的特性。数据归一化可以降低原始数据中较大范围的数据造成的影响，提高模型训练的速度和预测的精准度。本文采用min-max归一化方法使输入数据处于[0，1]之间，min-max的公式如下。

(13)

式中，xi—预处理输入数据；yi—标准化后的时间序列数据；max(xj)—数据的最大值；min(xj)—数据的最小值。

模型预测完成后需要对预测值进行反归一化，查看预测值和真实值的对比结果，反归一化函数如下。

y=min(xj)+yi{[max(xj)-min(xj)]}

(14)

以沙坪水电站2019年1月1日—12月31日间隔5min的实测数据为研究对象。这些数据集按月的顺序分为训练集和测试集。

(2)特征提取。通过CNN层获取数据蕴含的时间和空间状态特征。

(3)PSO参数初始化。设置粒子参数的初始值，随机设置例子的是初始位置和速度。

(4)自动参数寻优。基于PSO算法更新参数值、粒子速度和位置，达到最大迭代次数后，计算得到全局最优粒子，即LSTM的最优调参。

(5)初始化LSTM网络模型。输入PSO计算的最优调参。

(6)建立PSO-LSTM预测模型，进行预测模型的训练、验证、测试，输出预测结果反归一化结果。

(7)验证融合预测模型的结果，并进行模型性能评价。

5 结果与讨论

模型的精度通过均方根误差(RMSE)和纳什效率系数(NSE)来评断。在水量平衡模型中，本文最后采用了水位假设的迭代方法。模型的计算精度<0.1m3/s，最大迭代次数为200次。对于陷入局部无限循环的假设迭代，假设水位从前一时刻起没有变化。选取4个全天时段进行测试验证，水量平衡模型的测试精度见表2。

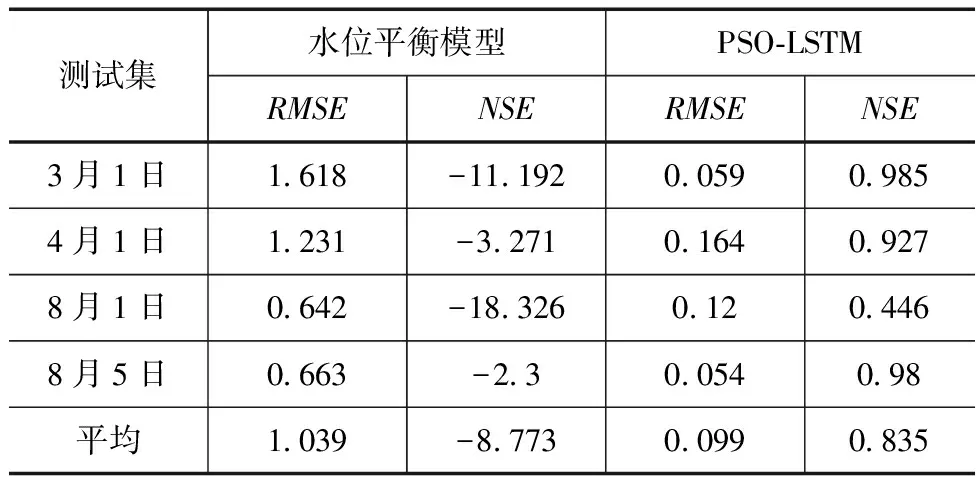
表2 2种模型的预测精度

在PSO-LSTM模型训练阶段，利用训练集数据对模型进行训练，并利用验证集数据对水库水位进行预测。训练阶段使用的模型超参数为128个隐藏单元，最大迭代次数为200次，学习速率为0.054168988。选取4个全天时段进行试验验证，PSO-LSTM模型的试验精度见表2。结果表明：水量平衡模型的最高RMSE为1.618，平均RMSE为1.039；NSE最高为-2.3，平均为-8.773。PSO-LSTM模型的RMSE最高为0.164，平均为0.099；NSE指数最高为0.985，平均为0.835。这些结果表明，PSO-LSTM的总体预测效果较好，水分平衡模型的精度较好。

6 结语

基于PSO-LSTM神经网络，构建了径流型反调节水电站水位快速预测模型。并利用沙坪II水电站进行水位预测，验证了模型的准确性。将得到的模型结果与基于水量平衡计算的预测结果进行比较，主要结论如下：PSO-LSTM神经网络处理的是多输入非线性模型的预测问题，建模方便，精度高。与基于水量平衡的预测模型结果相比，PSO-LSTM神经网络模型具有较高的预测精度。同时，该模型基于数据驱动，避免了水电站自身静态曲线对预测结果的影响，具有较大的实用价值。高精度的水位预测可为水电站调度优化、水资源合理配置和智能闸门控制提供重要参考。