改进的AR-LSSVM模型在河道水位预测中的应用

张 弘

(辽宁省铁岭水文局，辽宁 铁岭 112000)

非平稳时间序列数据是水文变量数据序列的主要特征，非平稳数据系列很难采用传统的数理统计学方法进行预测[1]。通常对于非平稳水文数据系列预测，往往是通过数据处理成平稳数据序列后再采用传统的数理统计学方法进行预测，这种预测的方式在国内应用也较为成熟[2-6]。这其中AR-LSSVM模型由于具有较好的收敛精度，在国内一些区域河道水位预测中得到应用，应用效果要好于传统水位预测数量统计学方法，且该模型对数据系列长度要求较低，一般序列长度达到30a即可满足模型计算要求。但传统AR-LSSVM模型对于非平稳数据序列经常出现无最优解的情况，降低了模型收敛计算精度。近些年来，有学者针对传统AR-LSSVM模型在模型求解存在的局限性，引入正交小波变化函数对传统模型进行改进，解决传统模型对非平稳数据系列适用性不强的问题，但改进的AR-LSSVM模型在水文变量序列中长期预测中还未得到相关应用。为此本文引入改进的AR-LSSVM模型，对铁岭清河开原站水位进行预测，并结合水文站实测水位数据进行精度对比。研究成果对于其他非平稳水文序列预测基于重要参考价值。

1 模型改进原理

通过对多个变量进行映射构建多变量拟合方程，其模型拟合方程形式为：

f(x，ω)=ωTφ(x)+b

(1)

式中，ω和Φ(x)—模拟拟合回归变量参数；b—变量阈值。

模型以拟合度和相对误差作为拟合方程的线性约束条件进行设置：

(2)

式中，ei—模型误差计算值，%；γ—非平稳数据序列值，m。

模型采用Lagrange函数对非约束化方程进行约束化转换：

L(ω，b，e，a)=J(ω，e)-
∑ai[ωTφ(x)+b+ei-yi]

(3)

模型求解函数方程为：

(4)

式中，a—模型计算因子。

对各求解函数按照非线性约束条件进行线性化转换计算：

(5)

式中，Ω—模型计算序列矩阵。

采用最小二乘支持向量机对模型计算序列矩阵进行线性拟合方程计算：

(6)

改进模型采用二进正交小波变化函进行变量重构计算：

X=D1+D2+…+DJ+CJ

(7)

式中，D—不同计算维度空间计算因子，D1={d1，1，d1，2，…}，…，DJ={DJ，1，DJ，2，…}；CJ={cJ，1，cJ，2，…}—不同空间维度下重构的计算因子。

采用二进小波变化方法对河道水位非平稳数据系列进行二次分解计算：

X=G1+G2+…+GN+XN

(8)

式中，G—2个维度变量空间下重构的求解方程，G1={g1，1，g1，2，…}，…，GN={g1，N，g2，N，…}。

不同时刻模型预测求解方程为：

Xi=g1，i+g2，i+…+gN，i+XN，i

(9)

在不同时间尺度下的预测值计算基础上，对不同时间状态下的水位进行推求：

XM+K=g1，M+K+g2，M+K+…+gN，M+k+xN，M+K

(10)

此外样本需要在预测时进行归一化计算：

(11)

2 模型应用

2.1 研究数据概况

将铁岭地区清河开原水文站近60a实测水位数据作为改进前后AR-LSSVM模型训练样本数据，并采用2013—2020年的实测月平均水位和年平均水位用于改进前后水位模拟精度对比。在采用模型进行河道水位预测前，对开原水文站近60a的水位资料分别进行可靠性、一致性、连续性的检验。所有年份水位资料数据均已通过资料检验，可用于改进前后AR-LSSVM模型应用。

2.2 月尺度河道水位预测精度对比

铁岭地区河流水位存在明显的季节变化，考虑到不同月份河流水位变化的差异程度，分别采用改进前后的AR-LSSVM模型对开原站各月平均水位进行预测，并结合实测月平均水位对预测值进行评估，评估结果见表1。

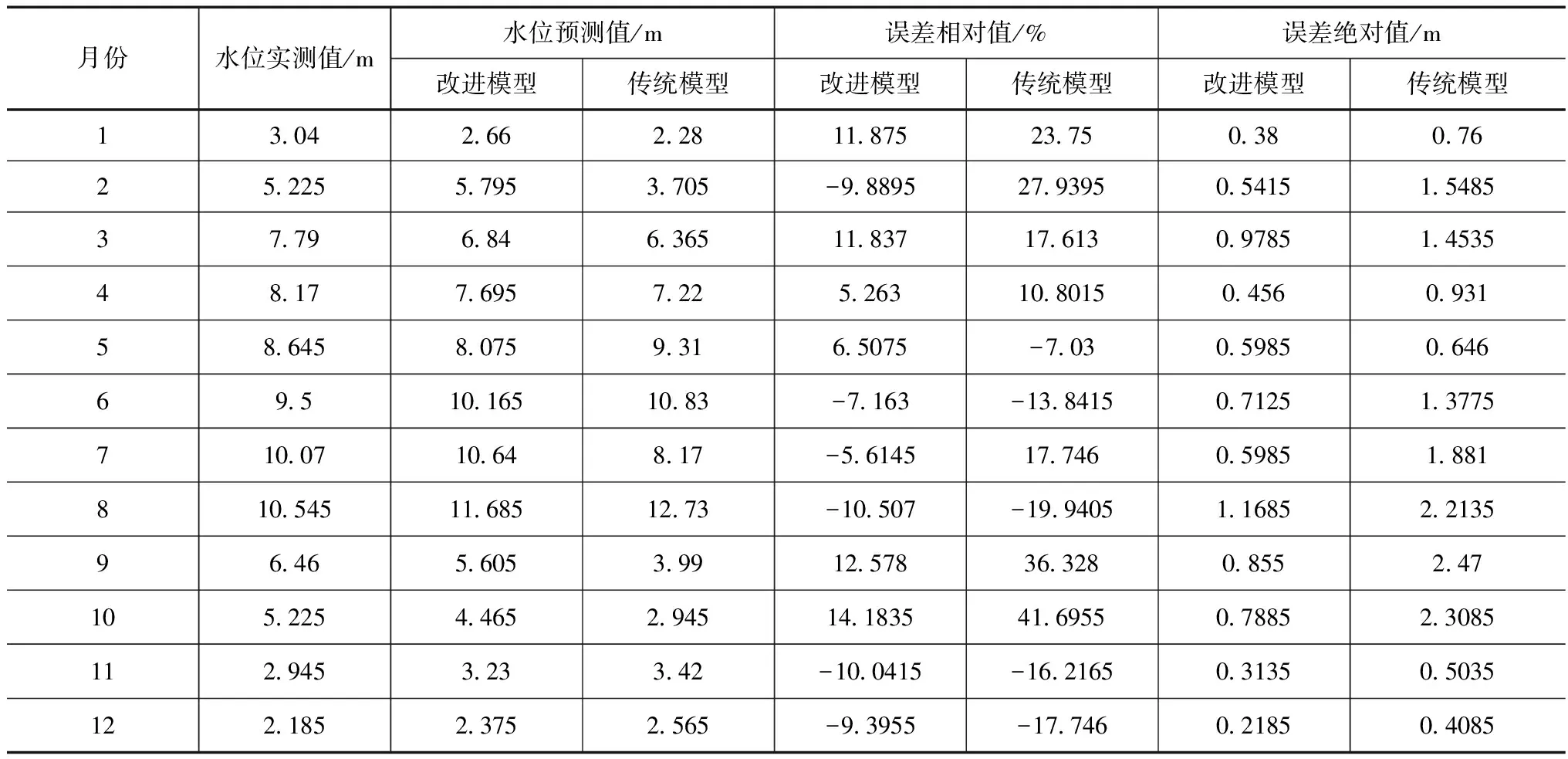
表1 月尺度下改进前后模型水位预测精度对比

对各月份不同模型河道水位预测值和实测值建立相关性分析和过程拟合分析，分析结果如图1—2所示。

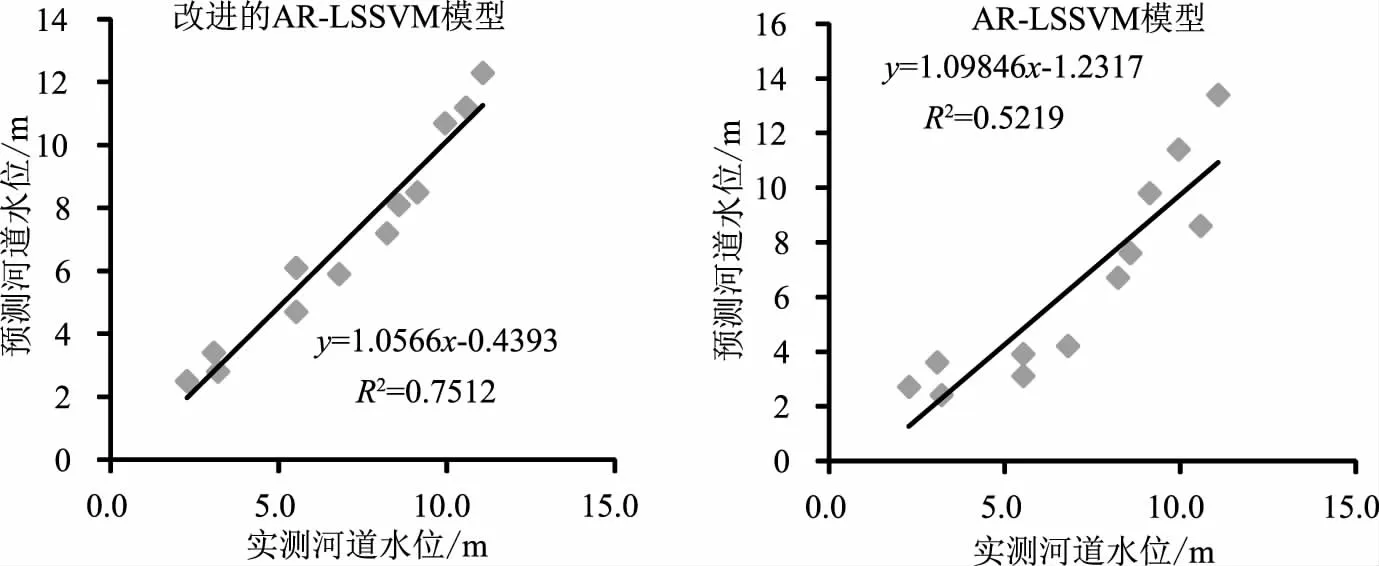
图1 月平均水位预测值和实测月平均水位回归方程

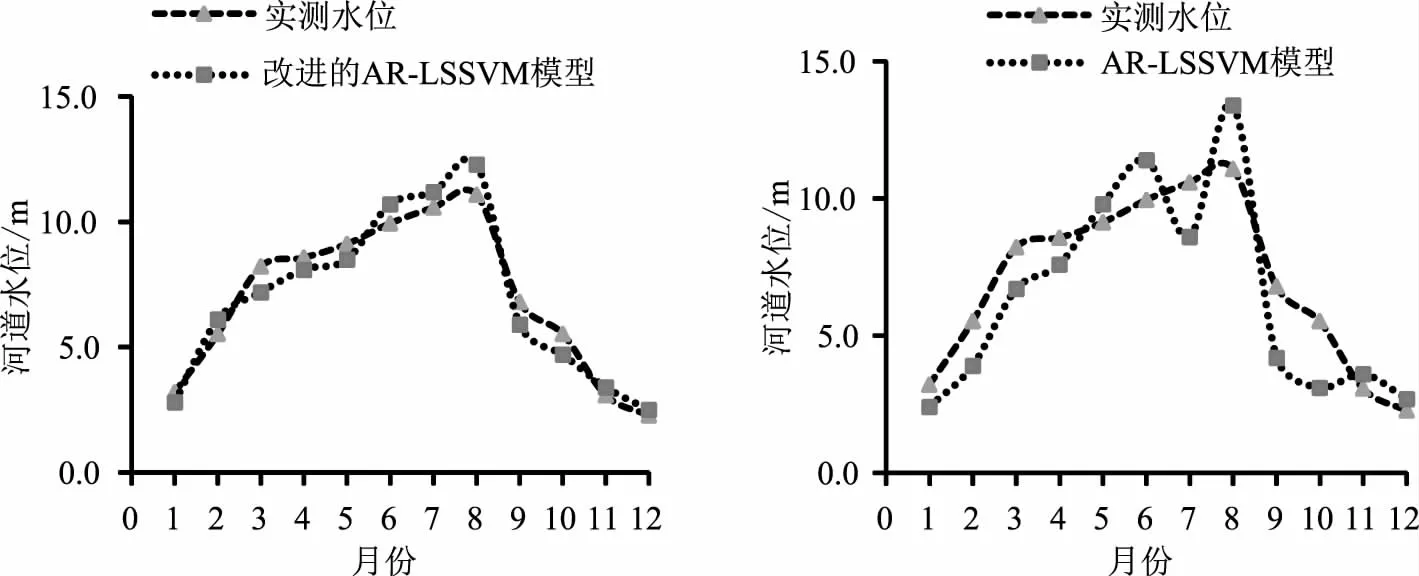
图2 月平均水位预测值和实测月平均水位过程拟合

从月尺度下改进前后模型水位预测精度对比可看出，相比于改进前，改进后的AR-LSSVM模型在各月河道水位预测精度均有明显改善，从相对误差指标可看出，改进后开原站各月份河道水位预测相对误差均在±15%范围内，而传统AR-LSSVM模型水位预测相对误差均要高于改进后的模型水位预测值，相比于改进前，改进后的开原站各月份河道水位预测误差平均降低11.3%。从各月份改进前后模型河道水位预测误差绝对值也可看出，相比于改进前，改进后模型预测的各月河道水位绝对误差均有减少，绝对误差均值平均降低0.74m，具有明显改善。这主要因为改进的AR-LSSVM模型引入正交小波变化函数对传统模型进行改进，提高模型收敛度，收敛度的提高也相应增加了模型求解的精度。

从改进前后模型对开原站月平均水位预测值和实测月平均水位回归方程可看出，相比于改进前的模型，改进后的模型水位预测和实际水位之间的相关系数提高0.2293。从改进前后AR-LSSVM模型水位预测过程和实际水位变化过程可看出，改进后模型的河道水位过程拟合度相比于改进前有明显提高。

2.3 年尺度河道水位预测精度对比

在月平均水位预测精度对比的基础上，结合开原站2013—2022年实测水位资料，对比分析改进前后AR-LSSVM模型在年尺度水位预测的精度，对比结果见表2。

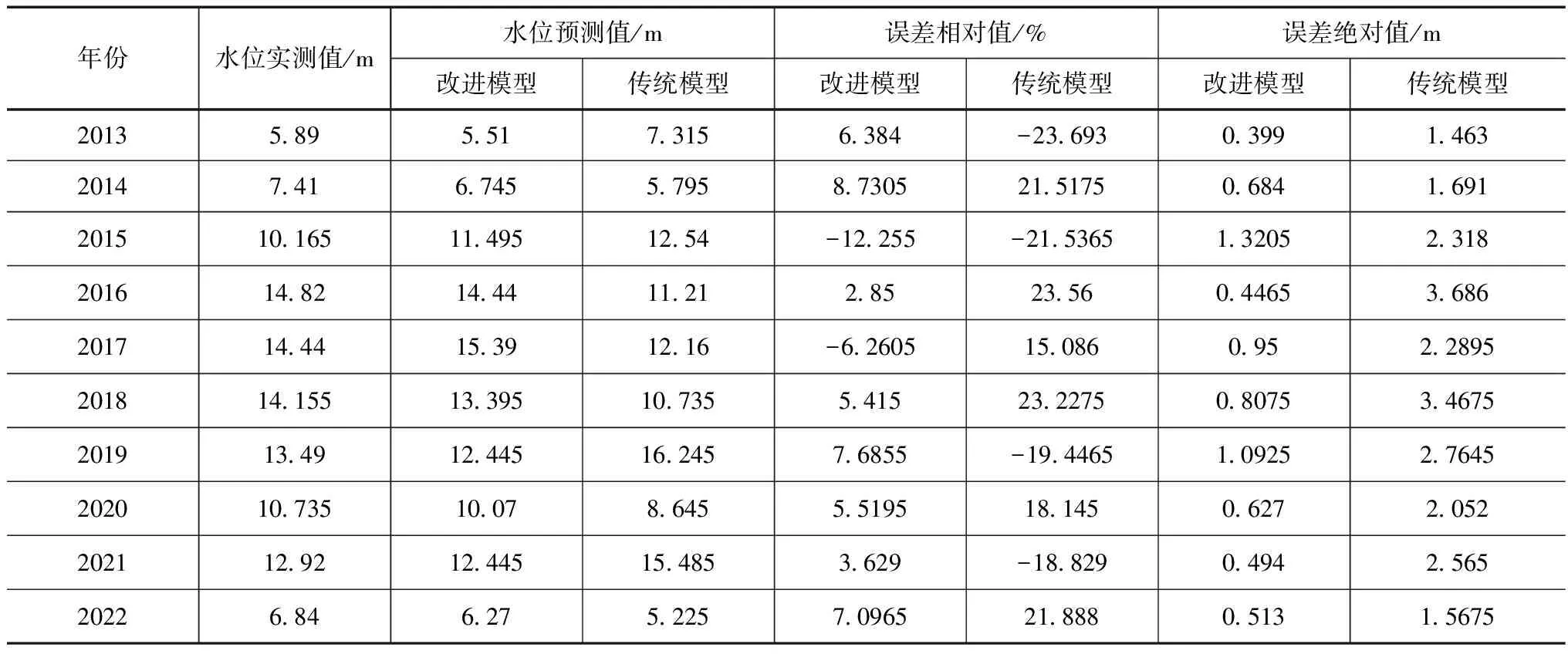
表2 年尺度下改进前后模型水位预测精度对比

对年尺度平均水位预测值和实测年平均水位之间的回归性进行分析，分析结果如图3所示。

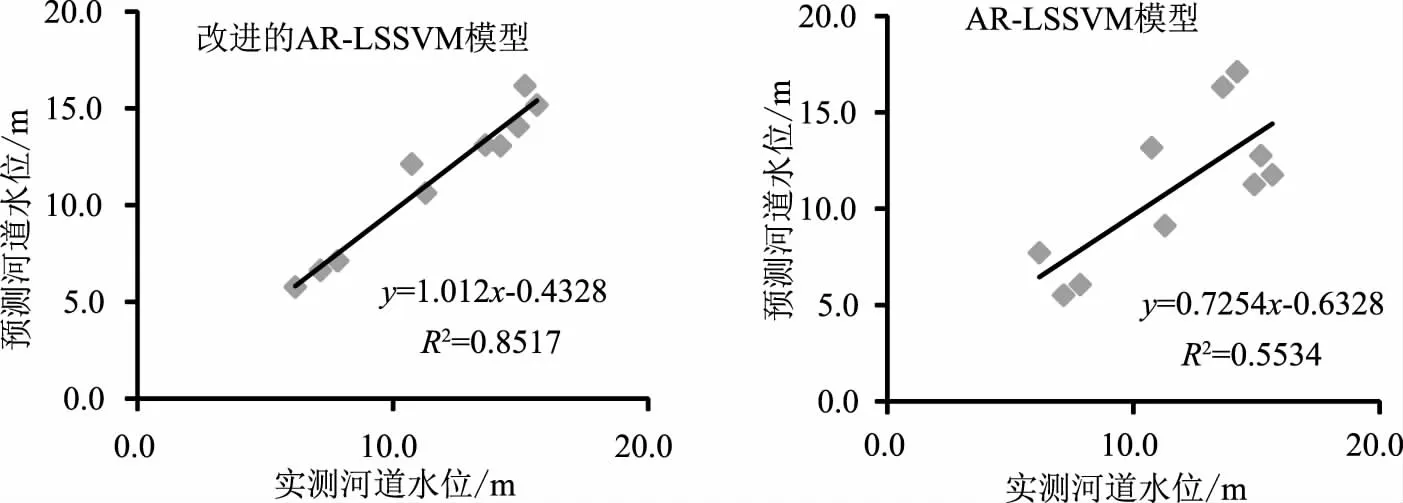
图3 年平均水位预测值和实测月平均水位过程拟合

从年尺度下改进前后模型水位预测精度对比，其改进前后AR-LSSVM模型在年尺度河道水位预测的精度总体要高于月尺度预测精度，这主要是因为年尺度河道水位预测由于均化影响，使得其预测精度要高于月尺度。相比于改进前，改进后AR-LSSVM模型预测各年份河道水位均化均有明显改善，各年份河道水位预测相对误差均值降低14.1%，绝对误差平均减少1.65m。从年平均水位预测值和实测月平均水位过程拟合可看出，相比于改进前，其相关系数提高0.2983。改进后AR-LSSVM模型相比于改进前模型，其年尺度和月尺度河道水位预测精度均得到明显改善，改进后的AR-LSSVM模型采用正交小波函数对模型变量进行优化组合后，提高了传统AR-LSSVM模型变量求解的精度，使得其预测精度得到改善。

3 主要结论

(1)在采用改进后AR-LSSVM模型进行河道水位预测时，可采用最小二乘方法对其样本数据序列矩阵进行优化计算，可提高模型非平稳数据序列拟合方程的回归系数，从而提高模型收敛求解精度。

(2)为有效剔除河道水位样本数据系列中的奇异值，可采用标准化处理的方法对河道水位样本数据系列进行预处理，从而一定程度降低河道水位样本数据序列的非平稳性。

(3)改进后AR-LSSVM模型对于日水位预测的适用性还需进一步探讨，此外对于中小型河流水位预测精度还需要深入分析。