施工参数对心墙砾石土渗透系数影响研究

张返成

(吉安市螺滩水利水电中心，江西 吉安 343060)

渗透系数可反应心墙堆石坝内部的渗流情况，该因素对大坝的力学性能及稳定性影响显著，近年来，许多专家学者针对心墙内部渗流情况开展相关研究。

张超萍等人[1]基于监测数据，对某心墙堆石坝的渗流情况进行监测，分析不同防渗效果对其渗流情况的影响，结果表明，防渗墙的防渗效果最好。许云鹏等人[2]基于土壤水分特征曲线，建立心墙堆石坝的渗流模型，分析该模型预测其渗漏系数的精度，结果表明，该模型可准确反应大坝内部的渗流情况，准确性较高。丁艳辉等人[3]对某水库大坝的渗流及变形规律进行监测，分析大坝顶部发生不均匀沉降的原因，结果表明，大坝内部渗流会导致坝顶变形，但是大坝总体稳定性及安全性较高。王芳等人[4]结合正交试验与数值模拟，分析库水位变化条件下，某心墙堆石坝的变形及渗流规律，结果表明，大坝变形与心墙内部的渗流情况有关，且与渗透系数呈正比。杨启贵等人[5]以某沥青混凝土心墙堆石坝为研究对象，对其坝体的渗流及稳定性进行计算，并分析动、静荷载下坝体的变形情况，并依据计算结果，对大坝进行设计，为后续渗流控制提供相关参考依据。

本研究以某水利工程的心墙堆石坝为研究对象，基于鲸鱼优化算法，构建渗透系数预测模型，分析各种因素对渗透系数的影响。

1 工程概况

本研究以某水利工程为研究对象，工程由大坝枢纽、供水工程两部分组成，大坝为面板堆石坝，防渗体为砾石土直心墙，最大坝高63.0m，坝顶高程1668.0m，坝轴线长121.84m。流域地处第二地形阶梯带，地貌属高原中山沟谷地貌类型，地下水由大气降雨及地表径流的补给，通过脉状流和岩溶管道流形式往低处排泄，最终呈分散状或集中形式排出地表补给下游河流。库区为沟谷地形，出露地层为峨眉山玄武岩组(P2β)的碎屑岩地层及第四系覆盖层，该地区不良物理地质现象总体发育较弱，主要表现为风化、岸坡卸荷、第四系堆积体等，分布在河流、沟谷两岸缓坡及坡脚地带。

2 渗透系数预测模型构建

本研究基于鲸鱼优化算法，构建渗透系数预测模型，分析各种因素对渗透系数(k)的影响，其目标函数如式(1)所示。

k=f(Cu，Cc，D5，D0.075，w，N0，N1，N2，H)

(1)

式中，Cu—不均匀系数；Cc—曲率系数；D5—粒径大于5mm颗粒质量分数，%；、D0.075—粒径小于0.075mm颗粒质量分数，%；w—含水率，%；Ni—碾遍次数，次；H—压实厚度，m。

采用最大信息系数(MIC)分析式(1)中参数对渗透系数的影响，其计算公式如式(2)所示。

(2)

式中，p—联合概率；I—互信息。

为分析不同参数对心墙砾石土渗透系数的影响，分别选取9组数据，对渗透系数进行预测，其输入参数见表1。

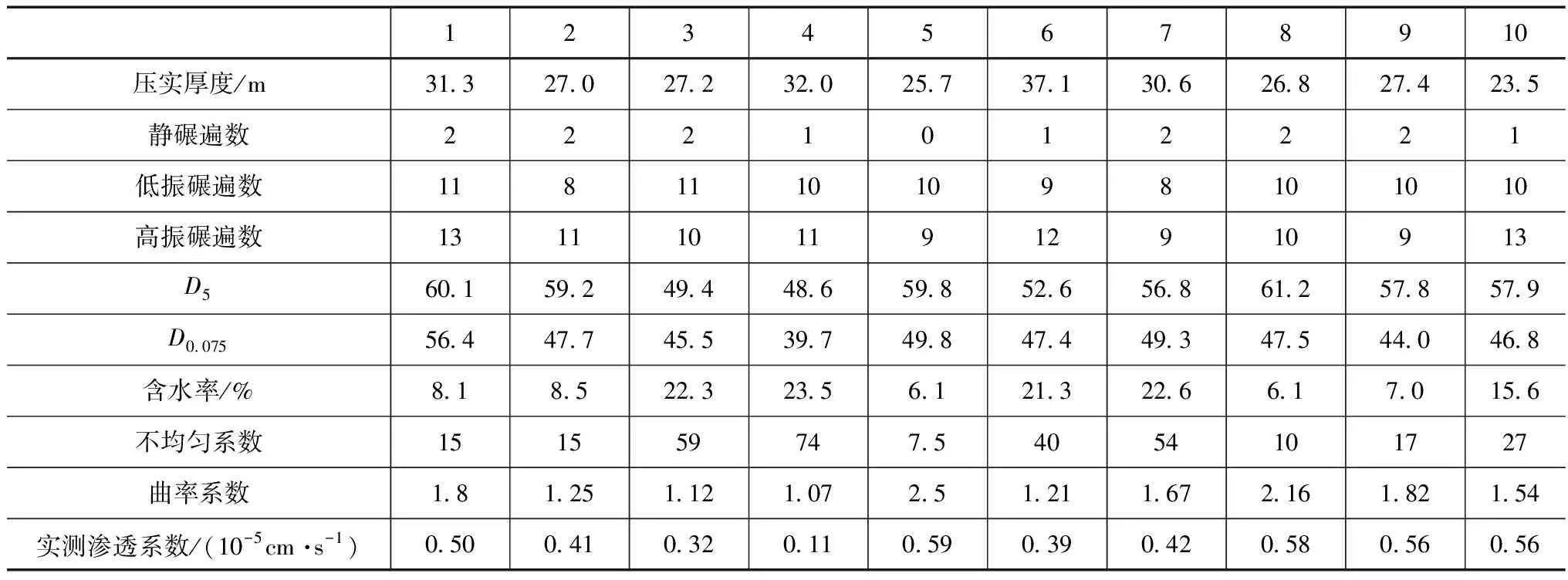
表1 输入参数

3 结果分析

BPNN模型和WOA-SVM模型是鲸鱼优化算法中两种常见的训练算法，为选取合适的算法模型对渗透系数预测模型进行训练，采用BPNN模型和WOA-SVM模型对渗透系数预测模型进行训练，并将其预测值与实际值进行对比，采用BPNN模型得出的测试样本编号-渗透系数曲线如图1所示。

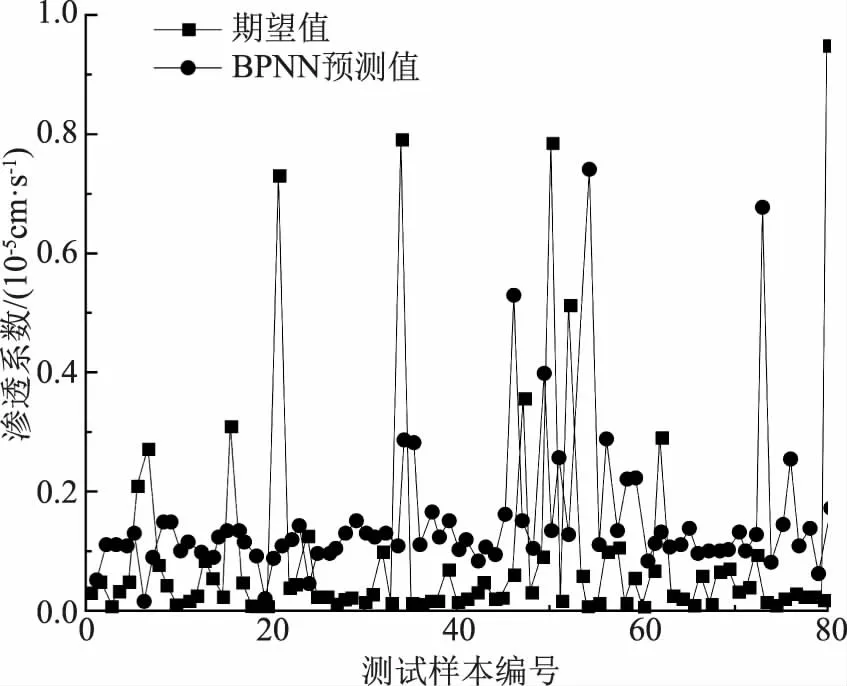
图1 BPNN模型的测试样本编号-渗透系数曲线

由图1可知，采用BPNN模型得出的渗透系数波动范围范围较大，其值集中于0～0.8×10-5cm/s间，渗透系数实际值的波动范围在0～1.0×10-5cm/s间，二者间的最大误差为0.7×10-5cm/s，最小误差小于0.01×10-5cm/s，说明采用该模型对渗透系数预测模型进行训练的效果较好，但预测值与实际值间仍存在一定的差异，预测精度存在改进的空间。

采用WOA-SVM模型得出的测试样本编号-渗透系数曲线如图2所示。

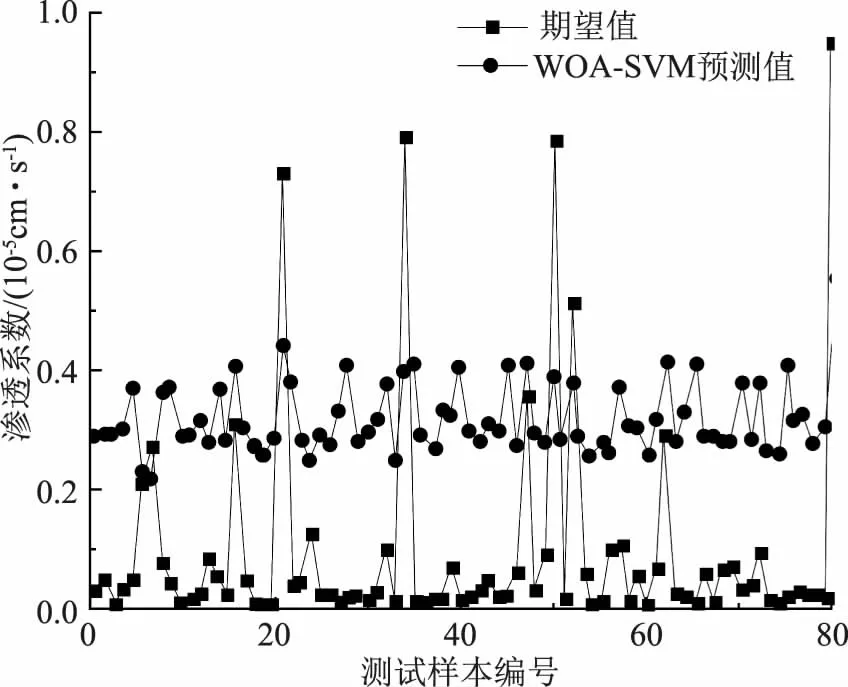
图2 WOA-SVM模型的测试样本编号-渗透系数曲线

由图2可知，采用WOA-SVM模型得出的渗透系数预测值波动范围较小，其渗透系数集中于0.2×10-5cm/s～0.4×10-5cm/s，采用WOA-SVM模型得出的渗透系数大多大于渗透系数实际值，二者间的渗透系数最大差值为0.4×10-5cm/s，渗透系数最小差值小于0.02×10-5cm/s，说明采用WOA-SVM模型对渗透系数进行预测的准确性良好。综合以上分析可得，采用WOA-SVM模型训练得出的渗透系数较为稳定，其波动范围较小，但是其预测精度劣于BPNN模型；采用BPNN模型训练得出的渗透系数波动性较大，但是其渗透系数预测结果与实际值间的差值较小；以上两种模型对于心墙砾石土的渗透系数的预测效果及精度良好，且各有优势，但是其预测精度仍存在可以改进的空间，为进一步提高渗透系数预测效果和预测精度，可以结合BPNN模型和WOA-SVM模型对渗透系数预测模型进行训练。

根据以上分析可得，结合BPNN模型和WOA-SVM模型可提高渗透系数预测的准确性，为进一步提高渗透系数预测效果和预测精度，对比分析BPNN模型和WOA-SVM模型结合得出的渗透系数预测结果与渗透系数实际值间的差异，测试样本编号-渗透系数曲线如图3所示。

由图3可知，采用BPNN-WOA-SVM模型得出的渗透系数预测值与实际值间的差值较小，且二者间的测试样本编号-渗透系数曲线变化趋势具有一致性，预测值与实际值间的最大差值为0.15×10-5cm/s，对比仅使用BPNN模型和WOA-SVM模型训练的渗透系数预测结果可得，结合2种模型进行预测误差减小了0.25×10-5cm/s～0.55×10-5cm/s，且预测结果较为稳定，BPNN-WOA-SVM模型对渗透系数预测的准确性提升效果显著。

为直观反映BPNN-WOA-SVM模型对渗透系数的预测效果，对采用不同模型预测的结果进行误差分析，误差分析结果见表2。

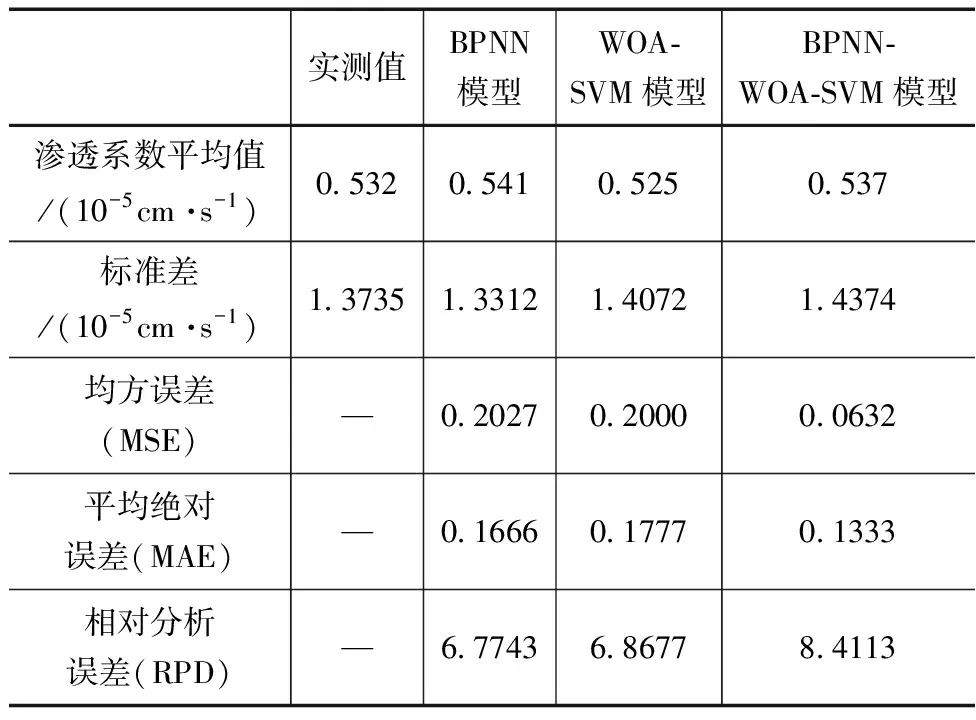
表2 误差分析结果

由表2可知，采用BPNN-WOA-SVM模型预测得出的渗透系数平均值与实测值间的差值最小，二者间的差值仅为0.5×10-7cm/s。通过不同模型的误差分析可得，BPNN-WOA-SVM模型的均方误差与平均绝对误差有最小值，说明采用该模型的预测准确性较高。采用3种模型得出的相对分析误差均大于2，说明以上模型的稳定性好，能够达到实际应用标准，其中，BPNN-WOA-SVM模型的相对分析误差最大，该模型的预测效果最好。

根据以上分析可得，采用BPNN-WOA-SVM模型对心墙砾石土的渗透系数进行预测的效果较好，为分析碾压施工参数对其渗透系数的影响，以表1所示的参数为研究对象，对渗透系数进行预测，将预测结果与不考虑碾压施工参数的预测值进行对比，其样本序号-渗透系数曲线如图4所示。

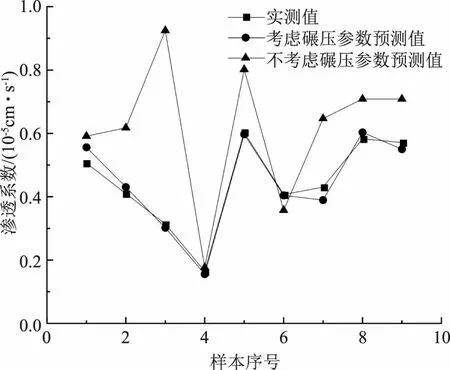
图4 样本序号-渗透系数曲线

由图4可知，不同碾压参数下的心墙砾石土渗透系数具有一定的差异性，其中，样本5的预测值最大，当考虑碾压参数预测值时，渗透系数为0.61×10-5cm/s，样本4的预测值最小，当考虑碾压参数预测值时，其渗透系数为0.17×10-5cm/s。对比是否考虑碾压参数下的心墙砾石土渗透系数可得，二者得出的渗透系数具有一定的差异性，其中，考虑碾压参数的渗透系数预测值与实测值间的差值较小，说明考虑碾压参数对心墙砾石土渗透系数进行预测更符合实际工程的情况，预测结果更加准确。

分析碾压参数对各仓面的渗透系数影响，见表3。

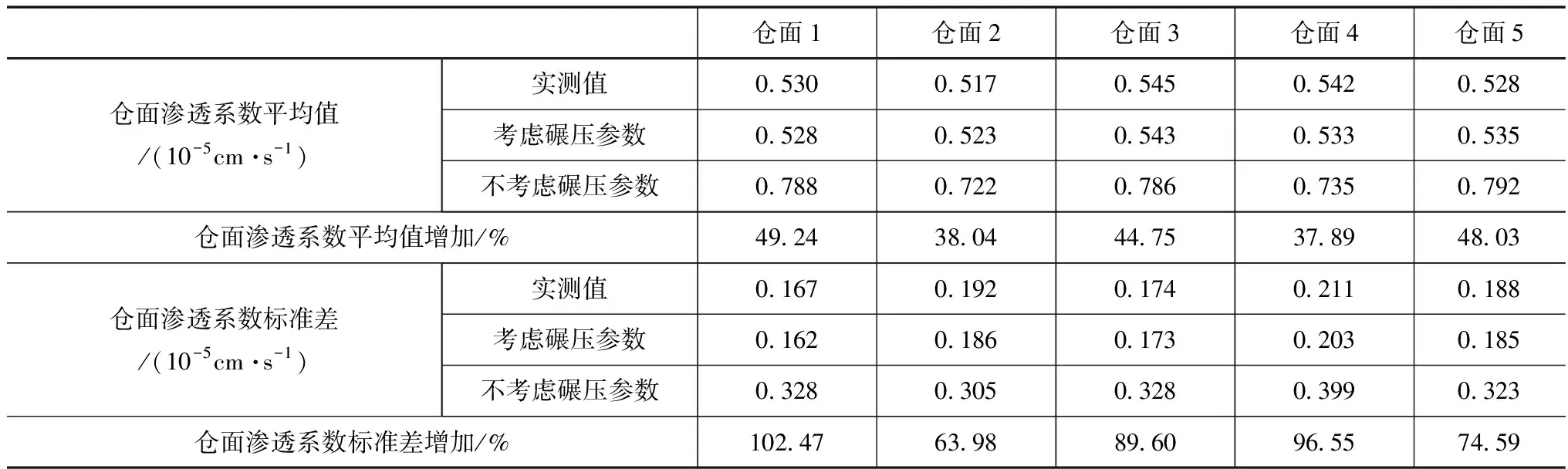
表3 碾压参数影响结果

由表3可知，考虑碾压参数的渗透系数与实测值间的差值较小，其中，仓面1与仓面3的预测精度最高，二者间的渗透系数平均值差值均为0.002×10-5cm/s，不考虑碾压参数的预测精度较差，与实测值间的渗透系数差值均大于0.2×10-5cm/s，说明碾压参数对心墙砾石土渗透系数的影响较大，为提高预测结果的准确性，应考虑碾压施工参数对渗透系数的影响[6]。

以表1中的参数为研究对象，对考虑碾压参数下的心墙砾石土渗透系数进行预测，对比不同模型下的预测结果，其样本序号-渗透系数曲线如图5所示。

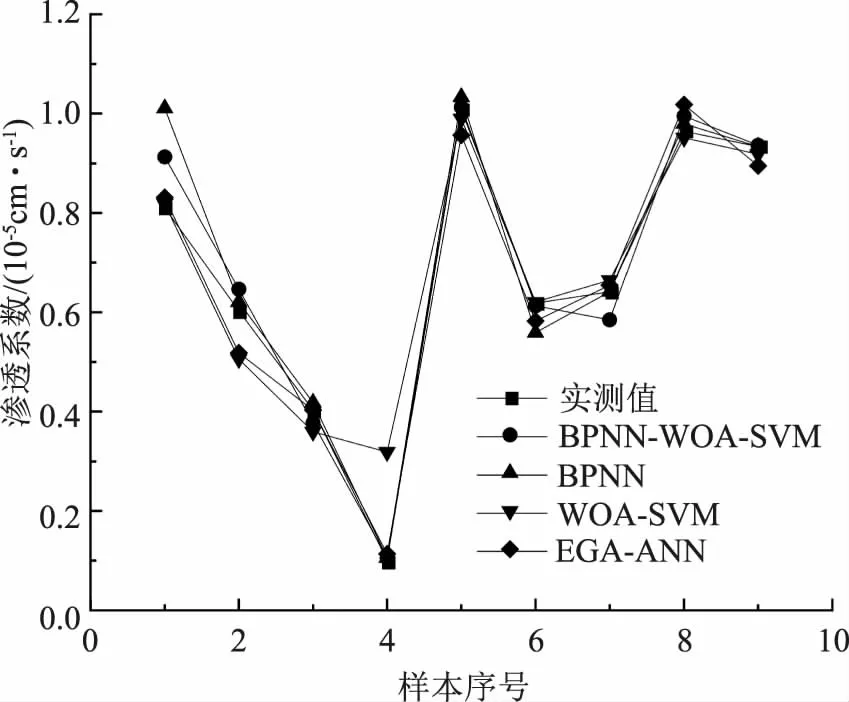
图5 样本序号-渗透系数曲线

由图5可知，采用WOA-SVM模型得出的预测结果与实测值间的差值最大，说明采用该模型对心墙砾石土渗透系数进行预测的精度最低，采用BPNN-WOA-SVM模型得出的样本序号-渗透系数曲线与实测值曲线的吻合度最高，说明采用组合模型可显著提升心墙砾石土的渗透系数的预测精度。

4 结论

本文以某心墙堆石坝为研究对象，基于鲸鱼优化算法，构建渗透系数预测模型，分析各种因素对渗透系数的影响，对比仅使用BPNN模型和WOA-SVM模型训练的渗透系数预测结果表明，单一模型与组合模型的稳定性好，能够达到实际应用标准，采用WOA-SVM模型得出的预测结果与实测值间的差值最大，精度最低，采用BPNN-WOA-SVM模型得出的样本序号-渗透系数曲线与实测值曲线的吻合度最高，模型预测结果较为稳定，得出的渗透系数预测值与实际值间的差值较小，对渗透系数预测的准确性提升效果显著。施工参数对心墙砾石土渗透系数的影响较大，为提高预测结果的准确性，应考虑碾压施工参数对渗透系数的影响。