基于博弈论的水利工程征地补偿量计算方法

唐维阳

(江苏省工程勘测研究院有限责任公司，江苏 扬州 225002)

随着近些年来水利工程建设力度的不断提升，其无论是在覆盖范围上，还是在工程规模上，都呈现出逐渐提升的发展趋势[1]。在此背景下，工程征地规模也随之增加[2]。就现阶段的水利工程征地补偿相关政策可以发现，其虽然针对不同的征地类型明确了具体的补偿标准[3]，但是对于具体计算方式的研究和分析仍存在较大的提升空间[4]。对于实际的水利工程而言，合理计算征地补偿量是保障项目能够顺利推进的基础；对于征地对象而言[5]，合理计算征地补偿量是保障其自身利益的关键；对于相关政府及建设部门而言，合理计算征地补偿量是保障政府经济支出符合社会发展的核心。在此基础上[6]，针对水利工程征地补偿量计算的相关研究也已经取得了一定的成果，其中，文献[7]以岐山县石头河防洪工程为研究目标，对具体的占地处理方法及补偿费用的计算方法进行分析，在一定程度上保障了各方经济利益的平衡，但是该方法的针对性较强，对于其他水利工程征地问题而言，适应性较低；文献[8]以单独选址项目为研究对象，在引入了动态经济价值的基础上，构建了征地补偿标准测算模型，在极大程度上提高了计算结果的可靠性，并具有较高的适应性，但是该模型对于基础数据的依赖性相对较高，一旦原始数据中存在数据缺失问题，其计算结果受影响较为明显。

在此基础上，本文设计了一种水利工程征地补偿量计算方法，并在计算过程中引入了博弈论。在以实际案例为基础的测试中，设计计算方法实现了对水利工程征地补偿量的合理分析。

1 水利工程征地补偿量计算方法设计

1.1 基于博弈论的水利工程征地补偿量影响因素分析

在计算水利工程征地补偿量的过程中，存在的主要的争议就是对于征地的类型划分问题，由于不同类型征地的补偿标准不同，因此，对应的补偿量也不同，为此，本文结合该问题，在分析水利工程征地补偿量影响因素的过程中引入了博弈论。但是需要注意的是，就争议问题展开研究的前提是在宏观上，参与博弈的各方能够达成以为[9]，为此，本文在分析水利工程征地补偿量影响因素时，设置了假定条件，具体见表1。

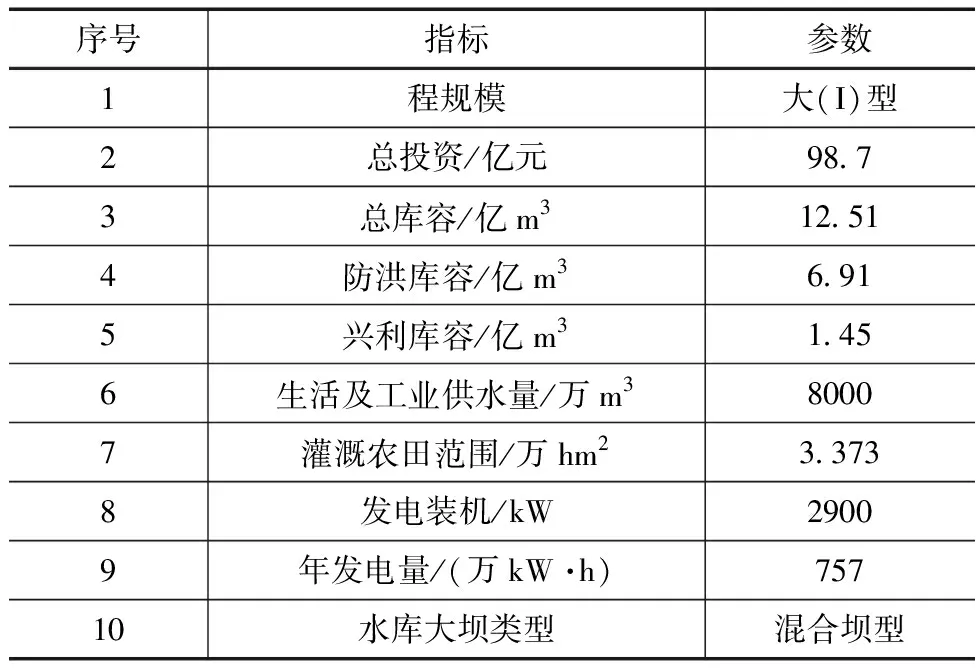
表1 测试工程参数信息统计表

表1 水利工程征地补偿量模型构建前提

在上述基础上，本文设置对水利工程征地补偿量影响因素的分析结果可以表示为：

p(x)={a1，a11，a2，a3，a41，a42，a51，a52}

(1)

式中，p(x)—水利工程征地补偿量影响因素的构成，即需要博弈的参量；a1—单位面积被征用地的总价值[10]；a11—单位面积被征用地支付农户的补偿量；a2—单位面积被征用地对于农户生存的消耗量；a3—在单位面积被征用地中，地方政府的价值占有量；a41和a42—地方政府与农户在博弈过程中，农户和地方政府的消耗系数，一般情况下，在征地意愿上，地方政府大于农户，因此，a41和a42的关系可以表示为a41

按照上述所示的方式，实现对水利工程征地补偿量影响因素的全面分析，为后续的计算提供执行基础。

1.2 水利工程征地补偿量博弈

结合上述对于水利工程征地补偿量影响因素的分析结果，本文分别从农户和地方政府的角度开展对具体补偿量的博弈。

首先，从农户开始博弈时，设置农户讨价参数为a11(o)，那么此时单位面积被征用地农民的净增收益可以表示为：

a51=a11(o)-a2

(2)

单位面积被征用地地方政府的净增收益可以表示为：

a52=a1-a11(o)-a2

(3)

根据式(2)和式(3)的计算结果，地方政府进行还价，假设还价参数为a11(s)，此时对应的单位面积被征用地农民的净增收益可以表示为：

a51=a41[a11(s)-a2]

(4)

单位面积被征用地地方政府的净增收益可以表示为：

a52=a42[a1-a11(s)-a2]

(5)

此时，农户在结合式(4)和式(5)的计算结果进行还价，对应的参数为a11，那么此时单位面积被征用地农民的净增收益和地方政府净收益分别可以表示为：

(6)

(7)

在此基础上，采用逆推归纳法从第三回合对补偿量进行分析，需要注意的是，在第三回合博弈时，最终决定权归农户所有，因此，逆推至第一回合的博弈阶段，均衡地方政府第二回合的期望利益，单位面积被征用地农民的补偿量可以表示为：

(8)

按照这样的方式，实现对水利工程补偿量的计算分析，使得各参与方的经济利益达到均衡状态。

2 应用测试

2.1 测试环境基本信息

在分析本文设计计算方法的可靠性时，以某实际的水库工程为基础开展了对比测试。对测试工程的基本概况进行分析，其中，水库的位置位于所在省市的境内，具体的坝址与市中心的距离为25.0km，控制的流域面积为2950km2，在对应流域规划中，其属于上游类的防洪控制工程类型。在功能设计方面，其以防洪为主要设计核心，在此基础上配合供水、灌溉功能，并在一定程度上兼顾发电功能，是所在流域重要的大型综合水利枢纽工程项目之一。工程建设及运行的相关参数信息见表1。

除此之外，结合水库所在地区的洪水情况，也对库容进行了针对性设计，具体情况如下：

(1)1000a一遇洪水的库容设计为8.92亿m3。

(2)10000a一遇洪水的库容设计为12.51亿m3。

以此为基础，针对移民安置工作，具体的资金总额为82.95亿元。本文以其中12户住户为测试对象，结合其原始居住情况，经济收入情况，占地情况，对具体的补偿量进行计算，并与实际的补偿结果进行比较。考虑到在对设计计算方法进行分析时，对比的方式更能体现其有效性，为此，分别设置文献[7]和文献[8]提出的方法作为对照组。

2.2 测试结果与分析

结合上述设置的测试环境，本文对于征地补偿量的计算综合了土地指标对于补偿量的影响，住宅指标对于补偿量的影响，生产资料指标对于补偿量的影响，家庭生活资料指标对于补偿量的影响以及二、三产业经济指标对于补偿量的影响，不同方法计算结果与实际补偿量之间的关系见表2。

结合表2所示的测试结果可以看出，在3种不同计算方法下，对于征地补偿量的计算结果与实际补偿量之间的差异存在一定的不同。在文献[7]方法的测试结果中，对于补偿量的计算结果呈现出了高于实际值的特点，其中，最大误差为4.11万元(9号测试对象)，最小误差也达到了0.99万元(5号测试对象)，整体误差达到了23.33万元，因此，从政府的角度出发，该方法对于水利工程征地补偿量的计算结果在一定程度上损害了其经济利益。对文献[8]方法的测试结果进行分析可以发现，其对于补偿量的计算结果整体呈现出了低于实际值的特点，虽然部分计算结果与实际值的误差仅为0.1万元(1号测试对象)，但是在误差分布上看，其在稳定性方面存在一定的提升空间，最大误差也达到了4.27万元(11号测试对象)，整体误差为19.04万元。因此，从居民的角度出发，该方法对于水利工程征地补偿量的计算结果也在一定程度上损害了其经济利益。对本文设计方法的测试结果进行分析，其不仅与实际补偿量保持高度一致，并且表现出了较高的稳定性，对应的最大误差仅为0.40万元(5号测试对象)，最小误差仅为0.03万元(1号测试对象和11号测试对象)，整体误差也仅为1.19万元。综合上述测试结果可以看出，本文设计的基于博弈论的水利工程征地补偿量计算方法可以实现对征地补偿量的准确计算，在极大程度上保障了各参与方的经济利益，对于实际的水利工程征地补偿工作的开展具有良好的应用和指导价值。

3 结语

在水利工程建设不断推进的过程中，对涉及征地问题的项目进行合理安置是极为必要的。本文提出基于博弈论的水利工程征地补偿量计算方法研究，充分考虑了不同土地类型对应的补偿标准，以及实际征地面积与工程施工面积之间的关系，在博弈论的支持下，实现了对工程征地补偿量的准确计算，在极大程度上了保障了水利工程征地补偿个参与方的经济利益。借助本文对于水利工程征地补偿量计算方法的设计与研究，也希望能够为相关实际工作的开展提供一定的借鉴价值，助力水利工程建设实现更好、更快发展。