带有p(t)-Laplacian和Erdélyi-Kober算子的分数阶边值问题的正解

薛 亮

(安徽工业职业技术学院 基础部,安徽 铜陵 244000)

0 引 言

分数阶微积分是整数阶微积分的拓展和延伸,带有边值条件的分数阶微分方程被广泛应用于工程和科学领域.因此,分数阶微分方程解的存在性问题在国内外具有极高的关注度,这类问题的研究对促进现实问题的解决有着巨大的价值[1-7]．近年来,有关p(t)-Laplacian算子的研究获得了极大的关注.该算子源于物理学,是一类非标准增长算子[8-11].例如,在文献[8]中,作者运用上下解方法研究一类p(r)-Laplacian方程多点边值问题解的存在性:

其中,-Δp(r)u=-(|u′|p(r)-2u′)′称为p(r)-Laplacian．然而,绝大多数的研究局限于p-Laplacian算子(p(t)恒为常数)[12-16]．例如,在文献[12]中,作者运用不动点定理和混合单调算子理论,研究Riemann-Liouville型分数阶微分方程积分边值问题正解的存在性和唯一性:

截至目前,很少有文献研究具有p(t)-Laplacian和Erdélyi-Kober积分算子的微分方程边值问题解的存在性.本文将研究以下分数阶积分边值问题:

(1)

其中,2<α≤3,0<β≤1,δ、η>0,λ>1,γ∈,CDβ为Caputo型分数阶导数,f∈C([0,1]×[0,∞),[0,∞)),φp(t)(·)为p(t)-Laplacian 算子,为Erdélyi-Kober型分数阶积分．

1 基础知识

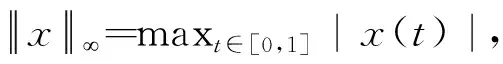
定义1[17]令f∈C((0,∞),),则f的δ阶Erdélyi-Kober分数积分定义为:

(2)

其中,η>0,γ∈.

定义2[1-2]令f:(0,∞)→,则f的α阶Caputo导数定义为:

其中,[α]为α的整数部分．

引理1[17]令δ、η>0,γ、q∈,则

(3)

引理2[18]对任意的(t,x)∈[0,1]×,φp(t)(x)=|x|p(t)-2x,是从到的一个同胚,对任意固定的t,关于x严格单调增长,且其逆算子定义为:

(4)

引理3[19]令2<α<3,λ≠2,y∈C[0,1],则边值问题

(5)

有唯一解,其可表达为:

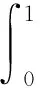
(6)

其中,

(7)

引理4令h(t)∈C[0,1],则边值问题

(8)

可表达为积分方程:

(9)

其中,

(10)

证明运用分数阶微积分运算性质,有:

φp(t)(CDαx(t))=-Iβh(t)+c.

(11)

注意到φp(t)可逆,则

(12)

将t=0代入式(12),并借助CDαx(0)=0,可得:

(13)

结合引理2可知c=0,从而根据式(12),可知:

由此可得:

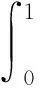
证毕．

引理5[17]令2<α<3,0<λ<2,则G(t,s)满足不等式:

(14)

定义集合P(θ,b,d)={x∈P:b≤θ(x),‖x‖≤d},Pc={x∈P:‖x‖≤c},其中b、c、d>0.

引理6[20]令P是Banach空间E上的一个锥,T:Pc→Pc是一全连续映射．若存在非负连续凹泛函θ,使得θ(x)≤‖x‖,x∈P和正数a

(Ⅰ) {x∈P(θ,b,d):θ(x)>b}≠φ且θ(Tx)>b,x∈P(θ,b,d);

(Ⅱ) ‖Tx‖

(Ⅲ)θ(Tx)>b,x∈P(θ,b,d)且‖Tx‖>b．

则T在Pc中至少有3个不动点x1、x2、x3．

2 主要结论

定义算子T:Pc→Pc:

(15)

定义非负连续凹泛函θ:

(16)

为方便起见,记

定理1若存在正数a

则问题(1)至少有3个正解.

因此,可得:

然后证明T是等度连续的.

对任意的x∈Ω,有:

因此,对任意的t1、t2∈[0,1]且t1

综上,根据Arzelà-Ascoli定理,可得T:Pc→Pc是一全连续算子.

若x∈Pc,则有:

这表明T:Pc→Pc.类似的,由定理1(Ⅰ)可得‖Tx‖

{x∈P(θ,b,d):θ(x)>b}≠φ.

若x∈P(θ,b,d),根据定理1(Ⅱ)可得b≤x(t)≤c,t∈[τ,1-τ]和

这说明引理6(Ⅰ)满足.当d=c,由引理6(Ⅰ)可得引理6(Ⅲ).至此,引理6的条件全部满足.因此,问题(1)至少有3个正解.

证毕.

例1考虑以下问题:

(17)

(18)

很容易验证(I1)～(I3)成立.因此,根据定理1,式(17)至少有3个正解．

3 结 语

本文运用不动点定理研究带有p(t)-Laplacian和Erdélyi-Kober积分算子的微分方程边值问题(1)多正解的存在性.先将问题(1)转化为与其等价的积分方程,再运用不动点定理考察由积分方程构建的算子方程,从而获得了原问题正解的存在性.