Improved complex modal superposition method with inclusion of overdamped modes

Chen Yong Donald M.McFarland Billie F.Spencer,Jr. Lawrence A.Bergman

(1College of Civil Engineering and Architecture,Zhejiang University,Hangzhou 310027,China)(2Department of Civil and Environmental Engineering,University of Illinois at Urbana-Champaign,Urbana 61801,USA)(3Department of Aerospace Engineering,University of Illinois at Urbana-Champaign,Urbana 61801,USA)(4College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou 310014,China)

Abstract：To address the involvement of overdamped complex modes that appear in a nonproportionally damped system,an improved complex mode superposition (ICMS) theory is proposed for forced vibration analysis,which suggests the use of exact modes in pairs for CMS-based dynamic analysis of whether the modes are overdamped or not.A typical nonproportionally damped system,namely,a cantilever beam with attached multiple arbitrarily placed external dampers,is considered an example because the first mode of the system is likely to be overdamped with the increase in damping.First,the relationship between the response in a complex modal space and the actual dynamic response is elucidated,based on which complete theoretical ICMS approaches for attaining time-domain response,transfer functions,and variances are expounded in detail.By decomposing the governing equation into real and imaginary parts,the original equation of motion in the complex domain is represented by an augmented state-space equation with real-valued matrices,which considerably reduces the difficulties observed in computing the time-varying response using complex-valued matrices.Additionally,for external excitations that can be regarded as filtered white noise,an efficient method for evaluating the variance response is proposed,which effectively reduces the computational cost.The results from the application of the proposed CMS-based methods are compared with those obtained by an assumed-mode (AM) method and finite element analysis (FEA).It can be found that the current results are closer to those obtained by FEA than those by the AM method.Finally,the optimal damping and optimal position of the dampers are investigated using an enumeration method,which reveals that the use of multiple dampers with small damping demonstrates a better effect than that of a single damper with large damping.

Key words：nonclassically damped system; continuous system; forced vibration; complex mode superposition method; overdamped mode; dynamic response

In the analysis of structures that exhibit natural modes of vibration,the presence of discrete energy-dissipation devices is recognized to disturb the mode shapes of the original system[1]and consequently leads to a nonclassically damped system (NCDS) if the Caughey-O’Kelly condition[2-3]is not fulfilled.Even today,the mode-superposition method remains attractive in performing a forced vibration analysis[4]owing to its remarkable qualities,such as conceptual simplicity and capability to reduce the order of a system by treating the vibration of the system as a linear combination of finite modal vibrations.The modal methods for NCDSs mainly fall into two categories: 1) Assumed-mode (AM) methods[4-14]in which approximate admissible shape functions,usually the mode shapes of the undisturbed system,are adopted; 2) Complex mode superposition (CMS) methods[15-24],which conventionally utilize the exact modes formed in a complex domain.The CMS method appears to be more promising because the complex eigenvalues and eigenfunctions,which yield a modal vibration with varying configuration rather than a constant configuration found in classically damped systems,are more suitable for characterizing the complicated dynamic behavior of NCDS[15].

Earlier studies on the use of complex modes mainly focused on discrete structures.One can be traced back to Foss[16],who proposed a theoretical approach where a structural motion could be expanded into a modal series,and the nonhomogeneous solutions of the dynamic system could thus be achieved.With regard to a nonclassically damped multi-degree-of-freedom (DOF) system,Veletsos and Ventura[15]elaborated on the application of the CMS method to free and forced vibration analyses in which a shear-beam-type three-story structure was introduced as an example.Recently,Zhao and Zhang[17]have proposed an acceleration technique where the CMS method that used truncated complex modes could be compensated.de Domenico and Ricciardi[18]introduced two real-valued measures to determine the number of complex modes to retain in a reduced-order model.

Although extensive studies related to the application of the CMS method to discrete structures have been conducted,the applicability of CMS for a continuous system remains limited,and only a few relevant studies can be found in the literature due to the lack of exact complex modes and corresponding natural frequencies of NCDS[19].Oliveto and Santini[20]derived the complex modes of a soil-structure system,which was simplified as two connected shear beams,and applied the CMS method to its dynamic analysis.Oliveto et al.[19]then extended the study to a simply supported Bernoulli-Euler beam with two rotational viscous dampers that were individually attached at the beam ends and investigated the dynamic behavior of the system undergoing free and forced vibration.By considering a Bernoulli-Euler beam with viscoelastic boundary supports at its ends,Fan et al.[21]demonstrated the complex modes of the system using complex stiffness coefficients,and the CMS method,in association with the derived complex modes,was then applied to obtain the dynamic response induced by harmonic excitations.By introducing an independent representation of the momentum for damped continuous systems,Krenk[22]formulated a general motion equation in a state-space form in which both the stiffness and damping operators were self-adjoint and symmetric.He considered a cable with a lateral viscous damper and a beam with two identical rotational viscous dampers attached at its ends for their case studies.For a pinned-pinned cable attached to rotational dampers and springs at their ends,Impollonia et al.[23]performed a CMS method-based time-domain dynamic analysis by splitting the modal decoupled equation of motion into real and imaginary parts.For the axial vibration of a rod with various arbitrarily placed viscous damping devices such as external (grounded),mass,and internal spring dampers,Alati et al.[24]demonstrated the exact closed-form eigenfunctions and characteristic equations and revealed that the CMS method,compared with the AM method,inherently satisfied the discontinuity conditions at the locations of the damping devices.Nevertheless,for the incorporation of overdamped modes,relevant development of the CMS method was not well elucidated in previous studies.The exact modes are commonly assumed to be complex conjugates; however,this is not true when overdamped modes are involved[25].

The current study presents theoretical approaches for forced vibration analysis in both the frequency and time domains using a multi-damper-beam system whose first mode is prone to overdamping with the increase in external damping[25].An improved CMS (ICMS) theory is proposed in the present study,in which the exact modes should be strictly used in pairs to decouple the vibration response,whether the modes are overdamped or not.A pair of overdamped modes consist of the modes that correspond to two real-valued solutions of the same characteristic equation.Consequently,pairwise exact modes must be adopted in converting the results in a complex modal space into actual vibration responses.For the convenience of the forced vibration analysis,the relevant methodologies presented herein are formulated in a state space.Moreover,the original continuous system is transformed into a reduced-order system by considering the presence of overdamped modes.For time-domain analysis,an augmented motion equation is proposed in which all of the matrices are real-valued,where the real and imaginary parts of the modal vibrations can be simultaneously obtained.For frequency-domain analysis,the transfer functions are found using Laplace transformation in association with modal decoupling techniques.An estimation equation for variance response is presented in terms of the variance response of a modal vibration.The modal variance response can be approximated by solving a Lyapunov equation in the modal space.The results are corroborated by finite element analyses (FEAs).Finally,we consider the random excitation by white noise located at the midspan.The optimal damping and optimal location are identified for two objective measures,namely,variance in dynamic response at the free end and spatial average variance.The formulas presented herein are nondimensionalized,which enables the identification of minimal sets of parameters that govern the inherent dynamic characteristics and facilitate the comparison of similar systems.

1 Problem Formulation

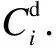
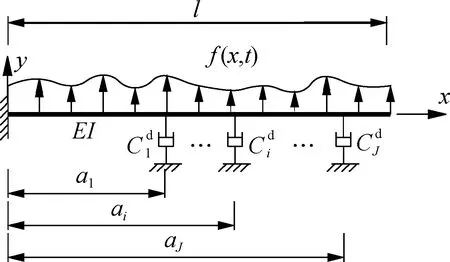
Fig.1 Cantilever beam with dampers and subjected to external excitation

By using d’Alembert’s principle,the governing equation of this system can be expressed as

(1a)

(1b)

whereδ( ) is the Dirac delta function,and Eq.(1b) accounts for the boundary conditions.Without loss of generality,Eq.(1) can be nondimensionalized by

(2)

Thus,we obtain

(3a)

(3b)

where

(4)

For free vibration,we obtain

(5)

By using separation of variables,the solution of Eq.(5) has the following form[25]:

(6a)

ω=jλ2

(6b)

(6c)

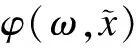
Subscriptsnandkdenote the sequential number of the modes,natural frequencies,or wave numbers,which are sorted using pseudoundamped natural frequencies in ascending order.Thus,Eq.(6a) yields

(7)

(8)

In a similar manner,thek-th mode expression is obtained as

(9)

Subtracting the integration of Eq.(8) that is premultiplied byφkfrom the integration of Eq.(9) premultiplied byφnyields the following:

ωk≠ωn

(10)

Similarly,subtracting the integration of Eq.(8) that is premultiplied byωkφkfrom the integration of Eq.(9) premultiplied byωnφnyields

(11)

Eqs.(10) and (11) are the first and second orthogonality conditions,respectively.

2 Reduced-Order System with Finite DOFs

Discrete systems with motion equations in a matrix form,which are achieved by applying the CMS and AM methods,are presented in this section.Note that the original system has infinite DOFs.Both the CMS and AM methods are capable of producing a reduced-order system with finite DOFs using the truncated modes.

2.1 CMS method

The CMS method lets the vibration response of the system be expressed as a linear combination of modal vibrations with corresponding natural frequencies.Thus,the vibration of the system is approximately expressed as

(12)

Let the following equations be true:

ψ={ψ1,ψ2,…,ψn,…,ψ2N}=

(13a)

(13b)

Λ={Λ1,Λ2,…,Λn,…,Λ2N}=

(13c)

whereψ,q,andΛare the modal,generalized coordinate,and frequency vectors,respectively.Thus,Eq.(12) can be rewritten as

(14)

where notation “°” is the Hadamard product operator.The displacement response can be computed using

(15)

The motion equation represented by Eq.(3) is thus re-expressed in the state space as

(16)

The operators in the coefficient matrices are found to be self-adjoint.Thus,Eq.(16) can be diagonalized by its eigenfunctions.

Substituting Eq.(14) into Eq.(16) and integrating Eq.(16),which is premultiplied by {ψk,Λkψk},yield the following:

(17)

Then,by applying the orthogonality conditions given in Eqs.(10) and (11),we have

(18)

We note that

(19)

Eq.(18) yields

(20)

As Eq.(20) holds for allk=1,2,…,2N,

(21)

where

Ω=diag(Λk)k=1,2,…,2N

(22)

B=diag(Bk)k=1,2,…,2N

(23)

(24)

whereΩandBare the state and input matrices of the system in a complex modal space,respectively;uis the input vector of the system in a complex modal space.

Eq.(21) represents a governing motion equation in a complex modal space and states that the original system can be decoupled.Then,the dynamic response governed by Eq.(3) can be approximated by solving Eq.(21).

We need to note that the response must be computed using Eq.(15) instead of the following:

(25)

which is frequently used in accordance with the assumption that the natural frequencies and modes are in conjugate pairs[20].This assumption does not hold for every NCDS because,in some cases,overdamped modes with low natural frequency will appear.

2.2 AM method

The orthogonality conditions for the modes of a cantilever beam with no attached damper (the undamped/undisturbed system) are expressed as

(26a)

(26b)

The vibration of a beam may be approximated using a truncated series ofNmodes as follows:

(27)

(28)

and

(29)

Substitution of Eq.(27) into Eq.(3) yields the following:

(30)

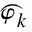
(31)

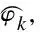
(32)

(33)

(34)

(35)

(36)

The damping matrix in which not all off-diagonal terms are zero implies that this system is NCDS.Accordingly,the eigenvalues and eigenfunctions obtained by Eq.(32) have complex values,and the natural frequencies obtained by Eq.(32) are approximations of those of the original system.Furthermore,the eigenfunctions of the original system can be approximately computed by

(37)

3 Methodologies for Dynamic Response

The formulations for the responses in the time and frequency domains based on the CMS and AM methods are presented in this section.Furthermore,the formulas for the variance analysis are provided.

We assume that the external excitation is separable,i.e.,in the following form:

(38)

The motion equations for both the CMS and AM methods can be generally formed in the state space as follows:

(39a)

(39b)

Thus,for the CMS method,the matrices in Eq.(39) are

(40)

whereIis an identity matrix.For the AM method,the matrices in Eq.(39) are

(41)

3.1 Time-domain analysis

In the CMS method,the initial conditions of the system satisfy the following requirement:

(42)

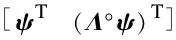
(43)

Thus,the vibration in the modal space induced by the initial condition can be expressed as

q=exp(Ω)q(0)

(44)

In the AM method,the initial conditions of the system satisfy the following:

(45)

(46)

In a similar manner,we can obtain

(47)

Eq.(41) shows that the reduced-order system in a modal space obtained via the AM method is described by real-valued matrices.Hence,the response of the system subjected to external excitation can be obtained via conventional means.In comparison,obtaining the response of the reduced-order system derived via the CMS method is more difficult because of the presence of complex-valued matrices.The following presents a transformation technique whereby the motion equation with complex-valued matrices can be transformed into one equation with real-valued matrices.

Eq.(39a) can be reformulated as follows:

(48)

Rewriting Eq.(48) in a state-space form yields

(49)

As the matrices in Eq.(49) have real values,Eq.(49) can now be easily solved.Accordingly,the output governed by Eq.(39b) is expressed as

(50)

3.2 Transfer function

As the system is linear,the multiple-input-multiple-output (MIMO) response can be regarded as the sum of a series of single-input-single-output (SISO) responses.Thus,the methodologies presented in the following for a SISO problem can be easily extended to that for a MIMO problem.

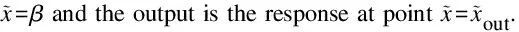
(51)

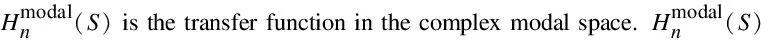
(52)

(53)

(54)

The transfer functions can be easily obtained by applying Laplace transformation to Eqs.(39) to (41).For a SISO problem,the shape function of the excitation in Eqs.(40) and (41) is

(55)

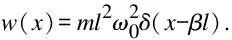
BF={ψ1(β),ψ2(β),…,ψ2N(β)}T

(56)

(57)

3.3 Variance

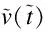
(58)

whereQcan be obtained by solving the Lyapunov equation

(59)

Thus,in the CMS method,the variance in the output can be computed using the following:

(60)

For the average of the variance response of the entire beam,namely,spatial average variance,we can obtain

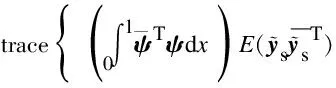
(61)

Eqs.(60) and (61),in which white noise is considered as an external excitation,can be easily applied to variance estimation of many stationary random processes,which can be regarded as filtered white noise.Subsequently,we introduce an example in which the random excitation is a band-limited white noise (BLWN).

BLWN can be regarded as white noise filtered by a band-pass filter in the following form:

(62a)

(62b)

The combination of Eqs.(62) and (39) leads to an augmented system,i.e.,

(63a)

(63b)

where

(64)

Thus,the covariance matrix of the beam-damper system herein subjected to BLWN is

(65)

whereQais the solution of the Lyapunov equation,i.e.,

(66)

Thus,the BLWN-induced response can be easily obtained by substituting Eq.(65) into Eqs.(60) and (61).

4 Numerical Study on the Dynamic Response

FEA is employed in this study to validate the proposed theoretical approach.The element utilized in FEA is an ordinary in-plane beam element.Thus,in FEA,the motion equation of the beam with attached dampers is formulated as

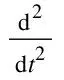
(67)

whereM,C,andKare the mass,damping,and stiffness matrices,respectively;Fis the vector of the external nodal excitations;yis the vector of the nodal displacements.The function of the dampers is introduced by revising dimensional damping matrixCaccording to the relationship between the dimensional and nondimensional damping expressed in Eq.(2).

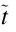
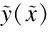
(69)

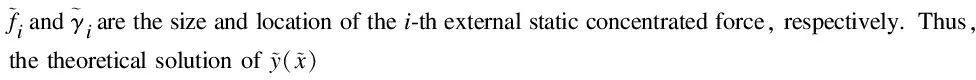
(70)

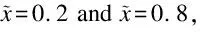
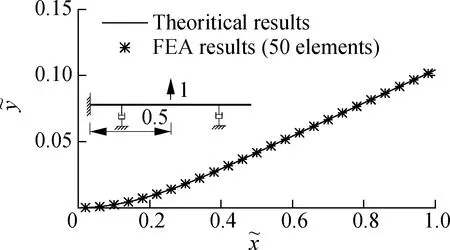
Fig.2 Static deformations caused by a unit concentrated force at the midpoint

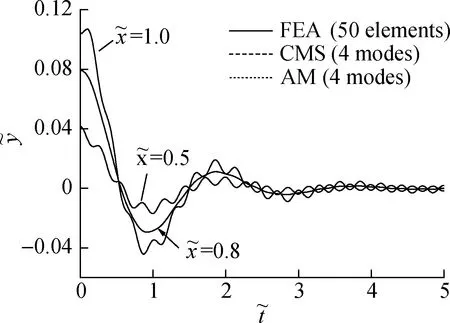
The static deformation shown in Fig.2 is set as the initial condition of the system.For the corresponding free vibration caused by the static deformation of the system shown in Fig.2,the time histories of the selected points are shown in Fig.3.The CMS results shown in the figure are those obtained by Eq.(44),and the FEA and AM results are those computed using the “lsim” function of MATLAB.The curves obtained by FEA and the CMS and AM methods are found to be very close,which validates all these three methods.Note that no overdamped mode is found in the case of small damping with a value ofc=1.0.The existence of overdamped modes in the large damping case (c=50.0) slows down the process of approaching the original equilibrium position from the initial disturbance.

(a)

Fig.4 shows the variance in the tip-displacement response and spatial average variance,which varies with the strength of the damper,with respect to the system shown in Fig.2.A concentrated force and a uniformly distributed force,which varies with time in accordance with a white noise with a noise intensity value of unity,are individually employed to excite beam vibration.We can observe that in terms of the variance response,the results obtained by the FEA,CMS,and AM methods are rather close.The curves of the variance in the free-end response exhibit a trend similar to those of the spatial average variance,although the former is naturally higher than the latter.Generally,as shown in Fig.4,the monotonically decreasing variance responses indicate that higher damping of the dampers can result in a smaller dynamic response.However,the efficiency of suppressing the vibration by increasing the damping decreases with increasing damping.

(a)

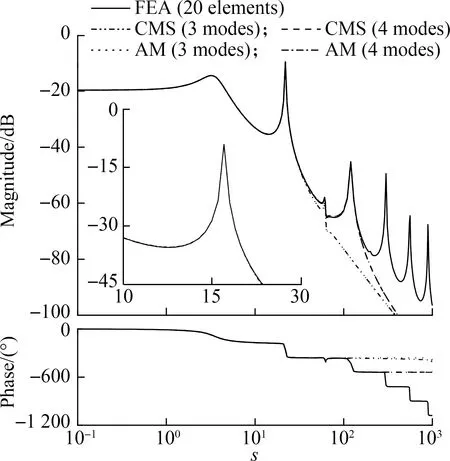
Fig.5 shows the transfer functions of a SISO system in which the damped beam shown in Fig.2 is considered.The input is a concentrated force at the midpoint of the beam,and the output is the displacement response of the free end.At small damping,the transfer functions obtained by the three methods are almost identical.However,when the damping is large,the transfer functions realized by the CMS method remain close to those obtained by FEA.However,the AM-method-based results show a large difference,implying that the CMS method performs better than the AM method in the frequency-domain analysis.

(a)

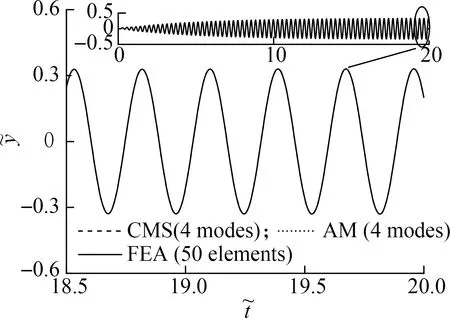
In the time domain,we find that the CMS method also provides a more accurate result than the AM method,especially when large damping results in the appearance of overdamped modes.Fig.6 shows the time histories of the tip vibration in the case of large and small damping,which considers the damped beam shown in Fig.2.A sinusoidal excitation with an amplitude of unity is applied to the midpoint in which the circular frequency of the excitation is equal to the imaginary part of the natural frequency that corresponds to the second mode.We find that the results of the three methods are very close in the case of small damping.However,in the case of large damping,the peak values of the curve obtained by the AM method are obviously smaller than those obtained by FEA.Meanwhile,the results based on the CMS method agree well with the FEA results.

(a)

A random vibration analysis is performed using a random excitation in the form of BLWN to further show the effectiveness of the CMS method.BLWN is generated by filtering a white noise with unit noise intensity.The nondimensional central frequency of BLWN is 27.5,and the bandwidth is 15; thus,the natural frequency corresponding to the second mode is covered.The filter is a Butterworth band-pass filter.The variance responses of the free end are shown in Fig.7,in which the employed system is the same as the damped beam shown in Fig.2.Once again,in the case of small damping,the results from the CMS,AM,and FE methods are very close,while in the case of large damping,the curves resulting from the FEA and AM methods are inconsistent.The divergence becomes more significant as the damping increases.In contrast,the difference between the results via the CMS method and FEA remains very small,which again highlights the superiority of the CMS method.

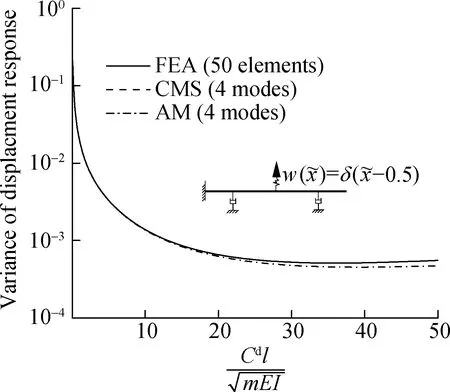
Fig.7 Variance of the displacement response of the free end

5 Optimal Damping and Locations under Random Excitation

The optimal locations and optimal damping of the dampers have been recognized to strongly depend on what types of optimization objective and external excitation are considered.For illustrative purposes,the optimization problem herein is related to a cantilevered beam with two attached identical dampers.The beam is subjected to a concentrated time-varying random force,which is a white noise with unit noise intensity.The enumeration technique is employed to perform this study in which the increments of the damping and damper location are 0.10 and 0.02,respectively.In other words,all the combinations of the nondimensional damping coefficients and locations of the dampers are investigated.

With regard to the variance response of the free end,the optimal installation that minimizes the variance is that the two dampers should be identically installed at the free end.For a spatial average variance,the variations of the least average variances from the nondimensional damping are shown in Fig.8(a),and the corresponding optimal locations are shown in Fig.8(b).The case ofα1=α2indicates that two identical dampers are installed at the same location,which is equivalent to the case of using a single damper but with double damping.The curves resulting from the CMS and AM methods are fairly close.We find that in the case of small damping (c≤2.4),no large difference exists between the strategies of using one large damper and using two small dampers; these two strategies yield almost the same optimal location and effectiveness in vibration control.Whenc≤2.4,installing the dampers at the free end produces a minimum average variance.Whenc≥2.4,installing two dampers at distinct locations is better than installing them at the same location,i.e.,the use of two small dampers demonstrates better performance than the use of one large damper for vibration suppression.Moreover,as shown in Fig.8,the least average variance decreases with the increase in damping,provided that the optimal damping and optimal damping location are considered.

(a)

6 Conclusions

1) Compared with the AM method,the CMS method can better reflect the inherent complex dynamic characteristics in NCDSs and results in a reduced-order model with higher accuracy,provided that the same number of modes are considered for orthogonal decomposition of forced vibration.Nevertheless,once the overdamped modes,which are not complex conjugate,are involved,the conventional CMS theory for NCDS needs to be further modified.An ICMS theory is proposed in this study where the underdamped complex modes are complex conjugates,and a pair of overdamped complex modes consist of the modes that correspond to two real-valued solutions of the same characteristic equation.

2) Methodologies associated with the AM and CMS methods are presented in detail for the time-domain,frequency-domain,and variance analyses to facilitate the forced vibration analysis of NCDSs.With reference to the time-domain analysis,the original complex-valued state-space equation is transformed into an augmented real-valued state-space equation by splitting the original matrices into real and imaginary parts and reassembling the equation so that many existing methods for time-history analysis can be utilized.With regard to the response induced by the filtered white-noise excitation,a Lyapunov equation-based variance analysis method is proposed,which is capable of rapid computation.

3) A cantilevered beam with two attached identical external dampers is used for the numerical case study.The results from the ICMS method are compared with those from the AM method and FEA.We find that the results from the CMS method are closer to those from FEA,which highlights the superiority of the CMS method over the AM method in dealing with NCDSs.The study of optimal damping and optimal damper location using the enumeration method shows that given small damping of the damper(s),no difference is observed between the use of a single damper and multiple dampers; however,the latter performs better provided that the damping of the dampers is relatively large.