空间几何体体积的几种求法
韩萍


求空间几何体的体积问题侧重于考查棱柱、圆柱、圆台、圆锥、棱台、棱锥、球等简单空间几何体的特征及其体积公式.这就要求同学们熟记并灵活运用几个简单空间几何体的性质和体积公式.下面结合实例,介绍空间几何体体积的几种求法.
一、直接法
当遇到一些简单、常见、规则的空间几何体时,可以采用直接法求解.先观察几何体的结构特征,快速确定几何体的底面和高;然后直接运用棱柱、圆柱、圆台、圆锥、棱台、棱锥、球的体积公式来求其几何体的体积.
例[1].已知直三棱柱[ABC-A1B1C1]的侧面[AA1B1B]为正方形,如图1所示,[AB=BC=2],[E,F]分别为[AC],[CC1]的中点,[BF⊥A1B1],求三棱锥[F-EBC]的体积.
解:如图1,连接[AF],
由题意可知:
因为[AB⊥BB1],[BC⊥AB],[BB1?BC=B],
所以[AB⊥平面BCC1B1],所以[AB⊥BF],
二、等积法
当无法直接运用体积公式求得三棱锥的体积时,可以采用等体积法,即不改变三棱锥的体积,通过更换三棱锥的底面和顶点,来求得三棱锥的体积.一般地,可以根据题目的条件选择易于求得面积的底面与高,来求三棱锥的体积.
例[2].如图2所示,已知平面[PCBM]为直角梯形,[∠PCB=90°],[PM∥BC],[PM=1],[BC=2],[AC=1],[∠ACB=120°],[AB⊥PC],直线[AM]与直线[PC]所成的角为[60°],求三棱锥[P-MAC]的体积.
解:设点[N]是[BC]的中点,如图2,
所以平面[PCMN]为正方形,
又因为[MN⊥平面ABC],所以[∠AMN=60°],
要求三棱锥[P-MAC]的体积,需求得底面[PCM]的面积以及点[A]到底面[PCM]的距离,但很难求得点A到底面的距离,而[VA-PCM=VA-MNC=VM-ACN],于是采用等体积法,通过求得三棱锥[M-ACN]的體积,从而求得三棱锥[P-MAC]的体积.
三、割补法
当遇到的空间几何体的形状较为复杂时,往往可以将其分割或者补成几个规则的空间几何体,依次求出这几个规则几何体的体积,再将所得结果进行相加减,即可求得复杂空间几何体的体积.
例[3].如图3所示,在多面体[ABCDEF]中,已知[ABCD]是边长为[1]的正方形,且[△ADE,△BCF]都是正三角形,[EF∥AB],[EF=2],求该多面体[ABCDEF]的体积.
解:如图3,分别过[A]、[B]作[EF]的垂线,垂足分别为[G]、[H],连接[DG,CH],即可将原几何体分割为两个三棱锥和一个直三棱柱.
本题中的图形为不规则几何图形,无法直接求得其体积,于是采用割补法,将其分为两个三棱锥和一个直三棱柱,利用椎体和棱柱的体积公式求出三者的体积,并将其相加,即可得到多面体[ABCDEF]的体积.
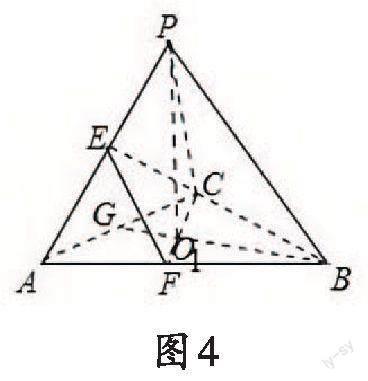
例[4].已知三棱锥[P-ABC]的四个顶点都在球[O]的球面上,且线段[PA=PB=PC],[△ABC]是边长为[2]的正三角形,[E,F]分别是[PA,AB]的中点,[∠CEF=90。],求球[O]的体积.
解:根据题意绘制图形,如图4所示.
因为[PA=PB=PC],[△ABC]是边长为[2]的正三角形,
所以三棱锥[P-ABC]为正三棱锥,
所以顶点[P]在底面的射影[O1]为底面三角形的中心,
连接[BO1],交[AC]于点[G],所以[AC⊥BG],
因为[PO1⊥AC],所以[AC⊥平面PBG],所以[PB⊥AC],
因为[E,F]分别是[PA,AB]的中点,所以[EF∥PB],
又因为[∠CEF=90°],即[EF⊥CE],
所以[PB⊥CE],[PB⊥平面PAC],
根据三棱锥[P-ABC]的几何特征:三条侧棱互相垂直且相等,将其补成为一个正方形,就能够根据正方体的特征,确定三棱锥的外接球的直径即为正方体的体对角线,从而快速确定球[O]的半径和体积.
总之,求解空间几何体的体积问题需注意:(1)灵活运用常见的空间几何体的性质以及体积公式;(2)将几何体进行合理的分割、补形,将复杂、不规则的几何体转化为简单的、规则的空间几何体,根据常见的空间几何体的体积公式快速解题.

