基于加权模糊的时序约束Petri网电网故障诊断方法

程学珍，庄学山，孟璐莎

（1.山东科技大学电气与自动化工程学院，山东青岛 266590；2.煤炭工业规划设计研究院有限公司，北京 100120）

0 引言

电网作为电力系统与用户直接相连的环节，其运行安全性关系到社会、生产、生活各个方面。电网发生故障后，调度中心收到大量报警信息，且可能伴随信息丢失、畸变等情况。根据报警信息快速判别出故障元件，能够为调度中心实时在线调控提供重要的支持，对电力系统可靠运行和快速恢复供电具有重要意义[1-2]。

目前，国内外对电网故障诊断的方法有专家系统[3]、人工神经网络[4-5]、贝叶斯决策[6]、Petri 网[7-10]等，但均存在一定缺点。专家系统过于依赖专家经验与知识库，知识库的维护存在难度；人工神经网络需要大量样本去训练模型，样本完备性难以保证；贝叶斯决策在先验概率获取上没有公认的有效方法；将模糊Petri 网应用于电网故障诊断中，虽弥补了Petri 网在故障诊断中不足，但没有充分利用报警信息，不能准确判别出故障元件。Petri 网是一种图形化建模的方法，因其具有逻辑严谨、推理过程简单、故障诊断速度快等优势，一直是电网故障诊断领域中的研究热点。

将报警信息包含的时间信息引入Petri 网中，能有效提高Petri 网的故障诊断能力。文献[11]提出报警信息不完备情况下的纠错算法，将时序信息应用于模糊Petri 网电网故障诊断中。文献[12]提出报警信息识别算法，提高了故障诊断的准确性。文献[13]提出虚拟有向弧及其应用规则，建立了改进的模糊Petri 网。文献[14]以故障发生时刻为起点，确立各初始库所的时序信息，通过时序检查进行初始置信度的修正。文献[15]将直觉模糊集理论引入到Petri网中，使得Petri 网在处理不确定信息时具有更高的准确性和容错性。文献[16]提出正反向的时序推理方法，修正不满足时序约束的报警信息初始置信度。文献[11-16]通过时序推理来检查不满足时序约束的报警信息，并修正其初始置信度。该类方法计算过程复杂且未充分利用时间信息。部分方法对于规模较大的电网，模型往往会生成维数较大的矩阵，造成计算量过大。

本文提出了一种基于加权模糊的时序约束Petri 网（Weighted Fuzzy Temporal Constraint Petri Net，WFTCPN）电网故障诊断方法，将时序约束引入到Petri 网的库所与变迁中，根据保护与断路器间的动作顺序关系建立WFTCPN 模型，模型对拓扑结构的变化具有较好适应性。研究时间区间与置信度相关联的分层推理算法，在置信度推理过程中，充分考虑到时间信息的影响，将时序推理与置信度推理同步进行。将子关联矩阵参与到矩阵的推理运算中，降低了矩阵维数，解决了计算量过大的问题。

1 WFTCPN模型相关定义

1.1 时序约束定义

电网发生故障后，收到的报警信息主要为保护、断路器的动作状态及其动作时间。报警信息（p，tP）表示保护p 动作，其动作时间为tp，(CB,tCB)表示断路器CB 动作，其动作时间为tCB。由于继电保护的整定遵循逐级配合的机制，报警信息之间存在严格的时序约束。为了描述报警信息之间的时序约束，文献[17]定义了2 种描述时序约束的概念。

1.2 WFTCPN基本定义

WFTCPN 是一个十元组，定义为：

WFTCPN={P,R,F,I,O,w,u,α,T,D}

1）{P,R,F} 表示一个简单的标识网。其中P={p1,p2,...,pn} 是一个有限的库所集合，R={r1,r2,...,rm}是一个有限的变迁集合，F为流关系，pi是集合P中的第i个库所，rj是集合R中的第j个变迁，i=1，2，3，…，n，j=1，2，3，…，m，其中n为库所的个数，m为变迁的个数。

2）I=(Iij)n×m代表输入矩阵。若库所pi到变迁rj存在有向弧，则Iij=1 ；若不存在有向弧，则Iij=0。i=1,2,3,…,n，j=1,2,3,…,m。

3）O=(Oji)n×m代表输出矩阵。若变迁ri到库所pj存在有向弧，则Oji=1；若不存在有向弧，则Oji=0。其中i=1,2,3,…,m，j=1,2,3,…,n。

与传统的模糊Petri 网不同的是，WFTCPN 中库所和变迁都被赋予一个时间区间。库所的时间区间表示库所对应事件的时间点约束，变迁的时间区间表示相邻库所间的时间距离约束。一个简单的WFTCPN 模型如图1 所示，T(p1) 为库所的时间区间，D(p2,p1) 和D(p3,p1) 为变迁的时间区间。若p1，p2，p3分别为断路器、保护、元件，则T(p1) 为断路器报警信息中的时间信息，即动作时间，D(p2,p1)为保护动作后断路器动作的延时区间，D(p3,p1) 为故障发生后保护动作的延时区间。

图1 简单的WFTCPN模型Fig.1 Simple WFTCPN model

2 基于WFTCPN电网故障诊断模型

2.1 WFTCPN图形化建模

一个简单的电网系统结构如图2 所示，其中S是电源，T 是变压器，CB1—CB29是断路器，DG1—DG6是分布式电源，L1—L15是线路，B1—B12是母线。该系统的保护配置如图3 所示，其中断路器用方块来代表，保护用椭圆来代表，虚线箭头代表保护的出口断路器指向。

图2 电网系统结构图Fig.2 Power grid system structure

图3 保护配置Fig.3 Protection configuration for power grid system

图3 中，下标S,R 分别表示送端、受端，下标m,p,s 分别表示主保护、近后备保护、远后备保护。对于线路L2而言，L2Sm表示线路L2送端的主保护，L2Sp表示线路L2送端的近后备保护，L1Ss表示线路L2送端的远后备保护。

线路配有主保护、近后备保护和远后备保护，当主保护拒动时，近后备保护动作，断开对应断路器来切除故障。当主保护、近后备保护或对应断路器拒动时，远后备保护动作，断开对应断路器来切除故障。

故障发生后，保护会在一定的延时区间内动作，保护动作后，相应的断路器会在一定的延时区间内动作，故障发生到保护动作到断路器动作存在固有的时间顺序约束关系。通过倒推的方法，可以根据各事件之间固有的延时关系，对报警信息进行分析，由断路器的信息推出保护的信息，进一步推出可疑故障元件的信息。当保护或断路器拒动后，故障范围会进一步扩大，因此需要考虑故障可能蔓延的各个方向。

本文根据倒推的方法以及元件的故障蔓延方向来建立模型。线路的主保护和近后备保护共用一个断路器，其他保护各对应着一个断路器。以线路L2为例，线路L2有2 个故障蔓延方向，引入元件方向库所送端L2S和受端L2R，建立的WFTCPN 模型如图4 所示。图4 中，I1为P2与R1的子关联矩阵，I2为P3与R2的子关联矩阵，I3为P4与R3的子关联矩阵；O1为R1与P1的子关联矩阵，O2为R2与P2的子关联矩阵，O3为R3与P3的子关联矩阵。

图4 线路L2的WFTCPN模型Fig.4 WFTCPN model of line L2

当拓扑结构发生变化时，只需增加或删除图4中虚线部分中对应的库所和变迁，不会对整体造成影响，因此对拓扑结构的变化具有较好适应性。例如，当增加元件时，只需将对应带虚线的箭头变为带实线的箭头即可。

将时序约束引入Petri 网后，代表断路器的库所与代表保护的库所位于不同的层并具有明显的分层特征，彼此之间通过时序约束来关联。根据分层特征，可以按层对库所和变迁进行分组P={P1,P2,P3,P4}，R={R1,R2,R3} 。其中P1为元件库所，P2为元件方向库所，P3为保护库所，P4为断路器库所。例如在图4 中，P4={p11,p12,p13,p14,p15}，R3={r9,r10,r11,r12,r13} 。

相邻的库所与变迁之间通过子关联矩阵相联系，例如图4 中，P4与R3通过I3相联系，R3与P3通过O3相联系。线路L2的输入矩阵及其子关联矩阵、输出矩阵及其子关联矩阵如图5、图6 所示。

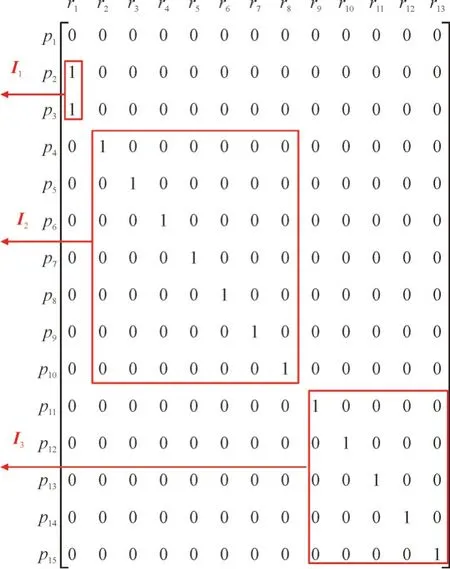
图5 线路L2的输入矩阵及其子关联矩阵Fig.5 Input matrix and its sub-correlation matrix of line L2

图6 线路L2的输出矩阵及其子关联矩阵Fig.6 Output matrix and its sub-correlation matrix of line L2

矩阵推理过程中，仅涉及到与库所和变迁相联系的子关联矩阵。显然，输入矩阵与输出矩阵是稀疏矩阵，含有大量的零元素，子关联矩阵只关注特定的矩阵块，从而忽略了大量没有意义的零元素，因此降低了矩阵维数，提高了推理速度，解决了模型存在的爆炸性问题。

2.2 模型参数设置

1）库所置信度：考虑到报警信息的不确定性，对于收到报警信息的断路器或保护，将其对应的库所赋予较高的初始置信度（无量纲）；为了防止拒动、误动、漏报等问题，对于没收到报警信息的断路器或保护，将其对应的库所赋予较低的初始置信度[18]，如表1 所示。

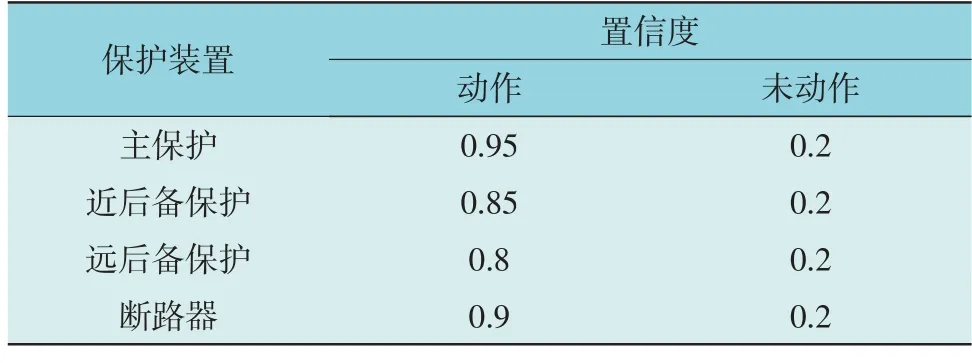
表1 库所初始置信度设置Table 1 Initial confidence setting of place

2）库所时间区间：对于收到报警信息且动作时间为T的断路器或保护，将其对应库所的时间点约束赋值为TP=[T,T]；对于没有收到报警信息的断路器或保护，将其赋值为TP=∅。

3）变迁时间区间：根据文献[19-21]对保护、断路器动作设定延时区间，D(tv,tm)，D(tv,tp)，D(tv,ts)分别表示故障发生后主保护、近后备保护、远后备保护动作的延时区间，D（tp，tCB）表示保护动作后断路器动作的延时区间。其对应的时间距离约束为：

式中：v 表示故障事件；p 表示各种保护。

4）权值与变迁影响因子：目前权值大都是根据专家经验设置，根据文献[16]，设断路器对应库所的输入权值为0.46，保护对应库所的输入权值为0.54。为了区分各保护对结果影响程度的大小，将主保护、近后备保护、远后备保护对应的变迁影响因子设为1，0.95，0.85。其他的权值与变迁影响因子设置为1。

5）高斯函数参数：文献[18]选择α=1.5 的高斯函数作为置信度的修正函数，其中α为高斯函数参数，x为输入值。如表2 所示，α=1.5时，输出值一直大于输入值，函数始终起到增强的作用，不利于进行故障诊断分析。α=3 时，当输入值x≤0.5，会得到更低的输出值，对不正确信息具有一定的抑制作用；当输入值x＞0.5，会得到更高的输出值，对正确信息具有一定的增强作用。因此本文选择作为置信度的修正函数。

表2 输出值与α 取值的关系Table 2 Relationship between output value and value of α

2.3 矩阵推理定义

1）设时间区间T0=[a,b]，T1=[c,d]，则：

式中：a，c为时间区间的下限；b，d为时间区间的上限；a，b，c，d均为实数；M(T0,T1)为时间区间的匹配函数。

2）设事件a的时间区间为T3，则：

3）若B=G(A)，其中A,B为n×m阶的实数矩阵，则：

其中，

式中：Aij，Bij为A，B的第i行第j列元素。

4）若C=A·B，其中A,B,C为n×m阶的实数矩阵，则：

5）若Tc=Ta×B，其中Ta,Tc分别为m×k,m×n阶的区间矩阵，B为n×k阶的实数矩阵，则：

式中：∩(*)为区间的求交集运算。

6）若E=mean(A,B,C′,Ta,Tb,D)，其中A,B,C′,D,E为m×n阶的实数矩阵，Ta,Tb为m×n阶的区间矩阵，则：

即：

7）若Tc=Ta⊕Tb，其中Tc为m×n阶的区间矩阵，则：

式中：∪(*)为区间的求并集运算。

式中：av(*)为求平均值运算。

式中：max(*)为求最大值运算。

2.4 WFTCPN模型推理过程

1）根据调度中心收到的报警信息，通过结线分析法[22]确定可疑故障元件，并建立可疑故障元件模型[23-24]。

2）根据收到的报警信息和可疑故障元件模型来设置初始值，可以确定变迁的时间区间，断路器和保护对应库所的时间区间、置信度，有向弧的权值、变迁影响因子。

3）将第四层库所的置信度和时间区间转移到第三层：此步骤实现断路器的信息向保护转移。

式中：αP4，wP4分别为第4 层库所的置信度、权值向量；TP4为第4 层库所的时间区间向量；DR3为第3 层变迁的时间区间向量，下标表示位于库所或变迁的第几层，后续出现的下标含义以此类推分别为通过第4 层信息推出的第3 层库所置信度、权值、时间区间向量。

4）将转移到第3 层的置信度和时间区间与第3层进行融合：此步骤实现断路器与保护考虑时间信息情况下的置信度融合，并将保护中的置信度和时间区间更新。

5）将第3 层库所的置信度和时间区间转移到第2 层：此步骤实现了各个方向库所的置信度和时间区间推理。

6）将第2 层库所的置信度和时间区间转移到第1 层：此步骤实现了各个方向库所的置信度和时间区间整合。

7）更新第1 层库所的置信度:此步骤考虑时间信息，并对元件库所的置信度进行更新。

式中：α为元件库所的置信度向量。

8）判断元件库所的置信度是否高于阈值0.65，若高于，则认为是故障元件，否则，则不是故障元件。

3 算例验证与比较

3.1 算例验证

算例1：调度中心收到的报警信息为(L2Sm,10 ms),(L2Rm,15 ms),(DG1s,970 ms),(L3Rs,980 ms),(CB3,41 ms),(CB7,1 000 ms),(CB6,1 010 ms)。

1）通过结线分析法对报警信息进行分析，得出线路L2为可疑故障元件，建立线路L2的模型，线路L2的模型如图4 所示。

2）通过调度中心收到的报警信息与线路L2的模型，根据2.2 模型参数设置来设置初始参数，可以得到变迁的时间区间为：

库所的时间区间为：

库所的置信度为：

权值和变迁影响因子为：

3）将第4 层库所的置信度和时间区间转移到第3 层：

4）将转移到第3 层的置信度和时间区间与第3层原本的进行融合：

5）将第3 层库所的置信度和时间区间转移到第2 层：

6）将第2 层库所的置信度和时间区间转移到第1 层：

7）更新第1 层库所的置信度:

8）得到线路L2的置信度为0.967，大于阈值0.65，为故障元件。

3.2 算例比较

文献[16]提出了一种基于时间约束的分层模糊Petri 网电网故障诊断方法，其与本文是考虑时间信息的方法。文献[25] 提出了一种基于分层模糊Petri 网电网故障诊断方法，是不考虑时间信息的方法。将本文提出的方法对图2 所示的电网系统结构进行多种故障场景的诊断测试，并与文献[16，25]所提方法的诊断结果相比较，结果如表3 所示。

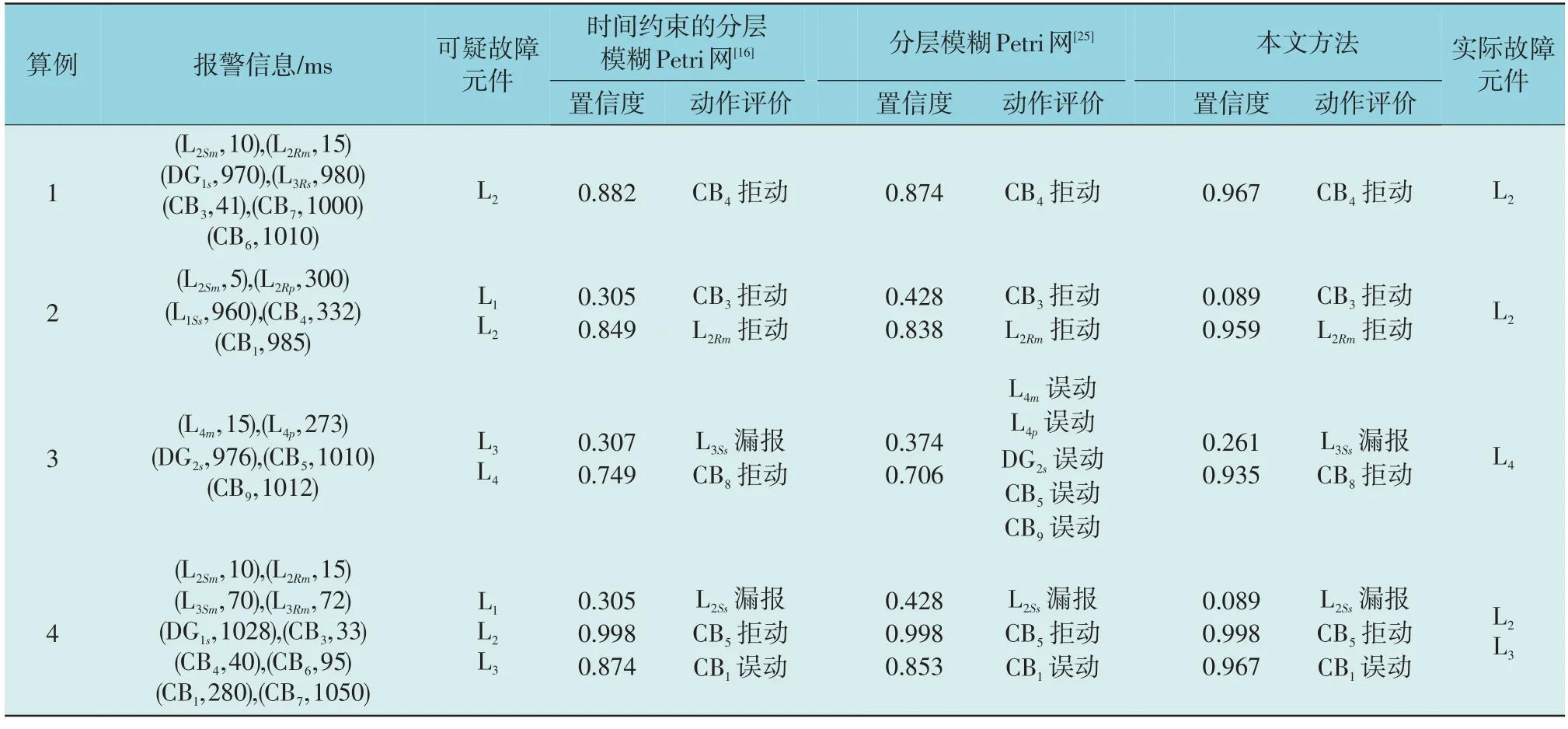
表3 基于WFTCPN方法的算例故障诊断结果Table 3 Fault diagnosis results of example based on WFTCPN method

其他算例的推理过程与算例1 类似，本文不再阐述。如表3 所示，算例1 为报警信息完备的断路器拒动的单重故障，算例2 为报警信息完备的断路器与保护均拒动的双重故障，算例3 为报警信息丢失的断路器拒动的单重故障，算例4 为报警信息丢失的多重故障，文献[16]、文献[25]、本文方法的阈值依次为0.65，0.75，0.65。算例1 和算例2 为简单类型的故障，因此各方法都可以准确的检查出来。算例3 中，基于分层模糊Petri 网的方法没有检测出故障元件。在算例1—算例4 中，本文方法均可检测出故障元件，说明本文方法在受到拒动、误动和报警信息丢失影响的情况下，能够准确判别出故障元件。

基于时间约束的分层模糊Petri 网方法采用正反向时序推理的方法对报警信息进行检查，将不满足时序关系约束的报警信息的初始置信度进行修正，再进行置信度推理。虽然基于时间约束的分层模糊Petri 网方法与本文方法诊断结果相同，但是本文方法在置信度推理中，充分考虑到时间信息的影响，将置信度与时间信息相结合，所以故障元件的置信度相对更高，非故障元件的置信度更低，这说明本文方法具有更高的准确性和容错性。置信度推理与时序推理同步进行，无需对报警信息进行逐项的检查，实现更快的推理。

4 结论

本文提出了一种基于WFTCPN 电网故障诊断方法，将时序约束引入到Petri 网中，定义置信度与时间区间分层推理运算。在置信度推理的过程中，同时考虑到时间信息的影响，将时序推理与置信度推理同步进行，有效避免了时序推理复杂的过程，能够快速得到可疑故障元件的置信度。矩阵推理过程中，子关联矩阵参与运算，降低了矩阵的维数，解决了模型存在的爆炸性问题。通过与多组算例比较得知，本文所提方法在误动、拒动、报警信息漏报等情况下均能迅速正确判别出故障元件，具有较高的准确性和容错性。