含高比例风电的新型电力系统的经济运行及储能配置

郭 峰，王 悦，陆 鑫，张世军，陈 婧，柳维刚，杨金龙

（1.国网陕西省宝鸡供电公司，陕西宝鸡 721004；2.国网信通亿力科技有限责任公司，福建福州 35000；3.三峡大学电气与新能源学院，湖北宜昌 443000）

0 引言

在“双碳”目标驱动下，以风电为代表的可再生能源将是新增装机容量的主力[1]。截止2022 年3 月底，我国可再生能源累计装机容量10.88×108kW，占全部装机容量的44.8%，其中风电装机3.37×108kW，占全部装机容量的13.9%。仅2022 年第一季度，我国可再生能源新增装机2 541×104kW，占全国新增发电装机的80%，其中，风电新增790×104kW[2-5]。

高比例可再生能源电力系统是实现双碳目标的重要途径之一，然而，由于可再生能源输出功率的强烈随机波动性，系统在运行过程中面临着功率实时平衡的挑战[6]。对于高比例风电替代的电力系统而言，风电出力具有明显的反调峰特性，即在谷时大发、峰时小发[7-8]。受这两方面因素的影响[9-10]，系统容易因功率不平衡而发生弃风、失负荷问题，影响系统运行的经济性和可靠性。随着风电替代比例的增加，系统功率不平衡问题将更加严峻。因此，对不同风电替代容量以及储能配置下系统的功率平衡及供电成本进行分析十分必要。

储能技术能有效提高电力系统消纳风力发电的能力[11]。储能可吸收多余的风力输出，并在风力发电量小于所需量时向系统注入电力[12]。现阶段储能成本仍较为昂贵[13]，利用储能平衡系统功率将增加系统运行成本，因此，在尽量减少弃风、不失负荷情况合理配置储能容量，方可保证高比例风电电力系统的经济性和可靠性[14]。为了提高风力并网的可靠性和可操作性，在文献[15]中采用了遗传算法和概率最优潮流算法优化储能配置容量以提高系统的经济运行能力。在文献[16]中提出了一种计及风力发电不确定性的多目标粒子群优化方法，用于储能选址和选型，改善成本最小化和电压曲线。文献[17-18]中提出了一个混合整数线性模型，用于储能设备的输电扩展规划。储能的最佳尺寸是根据节点功率平衡和负载持续时间曲线确定的[19]。文献[20]将云模型理论与k-means 聚类算法相结合来实现对储能系统的合理配置。然而，具体研究中尚未对高比例新能源场景下储能设备对电力系统的可靠性和经济性的影响情况进行分析。

随着风电替代比例增加，本文首先分析了电力系统的供需功率平衡情况，计算不同场景下系统的弃风和失负荷电量以及单位供电成本。针对不同风电替代比例下系统功率出现失负荷和弃风等问题，分别采用优化风电容量和配置储能容量等方式，以满足电力系统对于供电可靠性和经济运行的要求，计算不同风电替代比例对于单位供电成本的影响，以此为高比例可再生新能源系统的规划提供理论参考依据。

1 风火储的新型电力系统拓扑结构

新能源装机规模持续提升，而负荷仍将保持一定增长，实时电力供应与中长期电量供应保障困难更加突出，如何实现新型电力系统中“源-网-荷-储”的高效互动亟需深入研究。另外，随着光伏、风电等新能源为主体的新型电力系统的建设，电力系统的结构将发生深刻变化。新型电力系统供需双侧均面临较大的不确定性，电力平衡模式由“源随荷动”的发/用电平衡转向储能、多能转换参与缓冲的更大空间、更大时间尺度范围内的平衡。供需双侧运行特性对气候等外部条件的依赖性较高，针对传统电力系统建立的供需平衡理论亟需发展完善。

参考全国首个“风火储”沙戈荒新能源基地项目拓扑结构，本文所研究的风火储电力系统输送拓扑结构如图1所示。

图1 风火储电力系统输送拓扑结构Fig.1 Transmission topology of wind-coal-storage power system

由图1 可知，高比例风电替代的电力系统中，风电出力呈现强烈的随机性和波动性，对系统的功率平衡和可靠性有一定影响。因此，随着风电替代比例增加，需要通过储能的灵活性调节以及与源、储与荷的联动，实现电源、电网、负荷、储能各个环节的协调互动，实现系统安全、稳定、可靠的运行[21]。

2 含高比例风电电力系统的运行模型

2.1 不接入风电时的系统运行分析

用户负荷由系统内的多台火电机组供电，在系统日负荷曲线已知，且火电以最小成本运行时，需将负荷需求在火电机组间进行经济分配[21]。对火电机组而言，其运行成本取决于煤耗成本和运行维护成本，可以通过优化模型进行计算。

然而，对于传统火电机组间有功功率经济分配的必要条件是各机组的煤耗微增率相等。同时，在仅由火电机组供能的电力系统中，所有机组的有功出力之和要尽可能满足负荷需求。其中，火电机组的发电煤耗与其出力之间关系表达式如下：

式中：F1(Pi(t))为火电机组i在t时段的煤耗量；Pi(t)为火电机组i在t时段的有功出力；ai，bi和ci均为火电机组i的煤耗量系数；

将式（1）进行求导可得到各火电机组的耗量微增率。此时，系统内机组满足式（2）和式（3）所示关系。

式中：P1(t)，P2(t)，…，PN(t)为第1，2，…，N台火电机组在t时段的出力；N为系统内火电机组数量；a1，a2，…，aN，b1，b2和bN分别为第1，2，…，N台火电机组的煤耗量系数；L(t)为此时系统的负荷需求。

等微增算法能够实现火电机组出力的经济分配。然而，由于火电机组的最大和最小出力限制，在可运行区间内可能无法满足式（3），因此采用优化方法进行求解。

火电成本包括运行成本和碳捕集成本，其中运行成本由运行维护成本和发电煤耗成本构成，综合考虑火电综合运行成本，可得目标函数F的表达式如式（4）所示：

式中：T为调度时段；δ为调度步长；F2(Pi(t))为t时段机组i的运维成本；F3(Pi(t))为t时段机组i的碳捕集成本。

2.2 含不同比例风电系统的运行成本分析

由于风电功率具有明显的随机性、间歇性、反调峰等特点[22]，含高比例风电的电力系统源荷两端的供需矛盾将加剧，导致电力系统功率平衡问题愈发凸显。风电出力较小而负荷需求较大时更易发生失负荷（火电达到最大技术出力）；风电出力较大而负荷需求较小时更易发生弃风（火电达到最小技术出力）。由图2 可知，大容量风电接入将对系统的经济性及可靠性产生较大影响，有必要寻找合理的功率平衡解决方案十分必要。

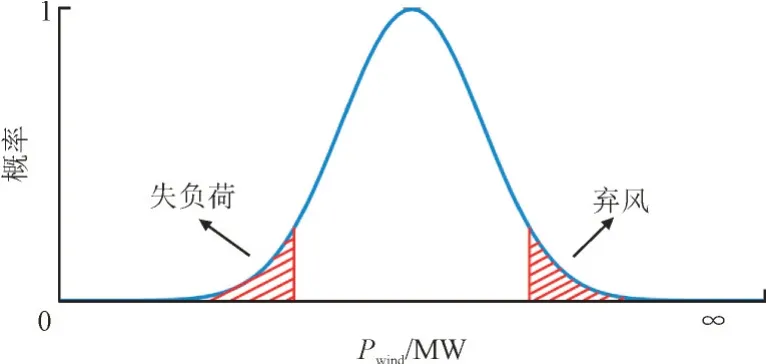
图2 风电替代增加系统的产生失负荷和弃风现象Fig.2 Lost load and wind abandonment of power system with high proportion of wind power

与无风电接入场景相比，风、火联合运行时需综合火电运行成本、风电运维成本和弃风成本，并以总成本最低建立目标函数，其表达式如式（5）所示：

式中：Pi(t)为t时段风电出力；Wp为风电装机容量；F4(WP)为风电运维成本；F5(Pw(t))为弃风成本。

因此，火电发电和风电成本的数学表达式为：

式中：Pw(t)为时刻t下风电供负荷功率；Pwf(t)为风电在时刻t的出力标幺值；Cw_o为风电机组单位电量运维成本；Cw_a为单位电量弃风成本。

同样，在电力系统运行过程中需要满足功率平衡约束，如式（8）所示：

此外，满足火电机组出力和风电机组出力约束条件表达式为：

式中，Pi，max和Pi，min分别为机组i有功出力的上下限。

2.3 含高比例风电系统储能容量的优化配置

在含高比例风电的新型电力系统内同时存在较大的弃风电量和失负荷电量，导致额外的系统成本。而储能作为保障系统功率实时平衡的有效手段可以在弃风时段进行充电，而在失负荷时段进行放电从而保障系统功率平衡[23]。但考虑到储能成本相对比较昂贵，过多配置储能也可能导致系统额外增加成本[24]。因此，本节在满足系统不失负荷的前提下，综合考虑系统的火电成本、风电成本、弃风失负荷成本以及储能成本进行分析，目标函数表达式如下：

式中：PBN为储能配置功率；EBN为储能配置能量；P（tB）为t时刻储能充电/放电值，计算如式（12）所示；F（6PBN，EBN）和F（7P（t8））分别为储能的投资成本和运维成本，数学表达式如式（13）和式（14）所示。

式中：γ1(t)和γ2(t)分别为储能在t时刻的充放电状态判断变量，取值为{0，1}，γ1(t)=1 表示在t时刻充电；γ1(t)=0 表示t时刻放电；Pin(t)表示t时刻储能的放电功率；Pout(t)为储能的单位功率投资成本；CB_P为储能的单位能量投资成本；NB为储能全寿命周期；CB_O为储能充放电单位能量的运维成本。

为保证储能不同时充放电，储能充放电状态判断变量应满足式（15）所示约束：

此外，为保障储能良好运行，还应满足充放电功率约束、储能的荷电状态约束、储存能量约束和全天充放电电量约束，表达式为：

式中：EB(t)为储能在t时刻贮存的能量；E（tB-1）为储能在t-1 时刻贮存的能量；EB(0)为储能的初始能量；为储能的充放电效率；SOC,max和SOC,min为储能的最大荷电状态和最小荷电状态。

联立相关约束，以式（11）作为目标函数进行计算，得到系统各机组出力、储能充放电状态和各时段容量以及弃风情况。

3 算例分析

风电功率的随机性、间歇性、反调峰等特点对电力系统运行经济性和可靠性都带来严峻的考验。因此，本文以全国首个“风火储”沙戈荒新能源基地项目为研究对象，所研究的电力系统由3 组火电机组、多种容量替代风电机组、1 组大型储能装置以及波动负荷组成。本文对5 种含风电系统的可靠供电进行定量分析，其场景设置如下（其中风电渗透率按题设所给计算方法：风电渗透率=最大风电功率与最大负荷功率之比）。场景1：含风电，风电渗透率为0%；场景2：300 MW 风电替代3 号机组，风电渗透率为33.3 %；场景3：600 MW 风电替代2 号机组，风电渗透率为66.7%；场景4：900 MW风电替代2 号、3 号机组，风电渗透率为100%；场景5：600 MW 风电替代2 号机组，考虑增设储能来提高系统供电可靠性。

本文研究系统包含火电、风电、储能和负荷，火电机组3 台、装机容量1 050 MW，其具体参数和运行成本如表1 和表2 所示。风电单位电量运行成本为0.045 元/kWh。

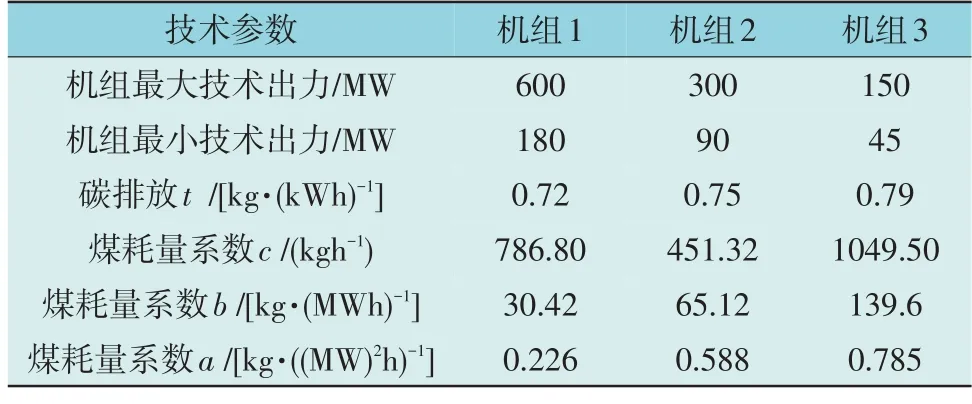
表1 火电机组相关参数Table 1 Related parameters of thermal power unit

表2 储能运行成本参数Table 2 Operating cost parameters of energy storage

3.1 考虑供电可靠性的系统单位供电成本分析

在风电替代容量增加时，采用系统的失负荷量来表征系统供电可靠性大小。在4 种含风电场景下，对不同含风电场景出现的失负荷成本进行统计，如表3 所示。

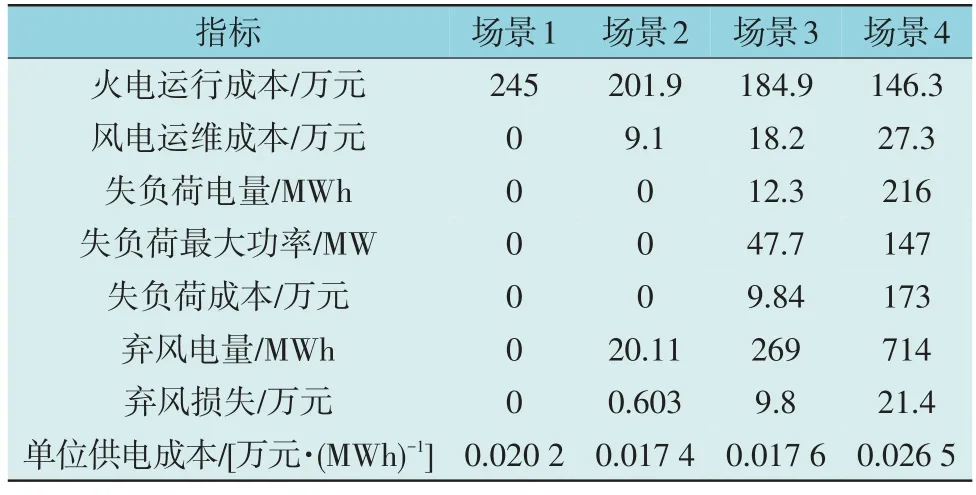
表3 不同风电场景下系统相关指标统计Table 3 Statistics of system indicators under different scenarios with wind power penetration

注：单位供电成本=系统总发电成本/系统总负荷电量，万元/MWh。

由表3 可知，在没有风电及风电替代容量较小时，火电机组技术出力完全能够满足负荷需求，不会出现失负荷情况。因此，场景1 和场景2 下系统的供电可靠性较高。当风电替代容量为600 MW 和900 MW 时，火电机组出力的调节范围有限，即使火电达到最大技术出力也无法满足负荷需求，导致系统出现失负荷。其中，场景3 和场景4 的失负荷电量分别为12.3 MWh 和216 MWh，失负荷最大功率分别为47.7 MW 和147 MW，可见风电替代容量增加会导致系统供电可靠性下降，失负荷成本也大幅度增加，进而导致单位供电成本不减反增。当采用增加风电装机容量以保证不失负荷时，随着风电渗透率增加，系统的单位供电成本也随之增加。因此，风电渗透率越小时，通过增加风电装机容量以保证可靠性更加经济。

给出场景4 下系统各机组出力情况如图3 所示，此时系统的弃风和失负荷情况如图4 所示。

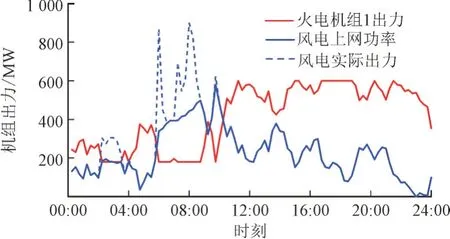
图3 电力系统接入900 MW风电时各机组出力Fig.3 Output of each unit in power system with wind power integration of 900 MW

图4 电力系统接入900 MW风电时系统的弃风和失负荷情况Fig.4 Wind abandonment and loss load of power system integrating wind power of 900 MW

由图3 和图4 可知，由于风资源分布与负荷用能的时序差别，系统内此时存在较大的弃风电量和失负荷电量，其中弃风时段主要集中于凌晨和晨间，此时风电出力相对较高，而负荷需求较低；失负荷时段主要集中于午间和傍晚，此时风电出力较低，而负荷需求较高。计算得到此时系统全天的失负荷电量为215.9 MWh，进而导致失负荷成本高达173 万元，极大增加了单位供电成本、降低了供电可靠性。

3.2 增加储能保障供电可靠性的运行经济影响分析

在含高比例风电电力系统内同时存在较大的弃风电量和失负荷电量，导致额外的系统成本。而储能作为保障系统功率实时平衡的有效手段可以在弃风时段进行充电，而在失负荷时段进行放电从而保障系统功率平衡。但考虑到储能成本相对比较昂贵，过多配置储能也可能导致系统额外增加成本[14-16]。因此，在满足系统不失负荷的前提下，综合考虑系统的火电成本、风电成本、弃风失负荷成本以及储能成本进行分析，求解最小储能容量的目标函数，得到系统各机组出力、储能充放电状态和各时段容量以及弃风情况如图5 和图6 所示。

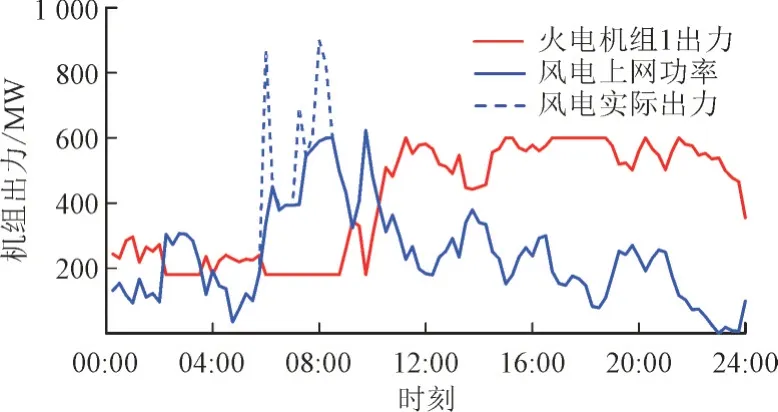
图5 系统加入储能后的系统机组出力Fig.5 Unit output of system after integrating energy storage

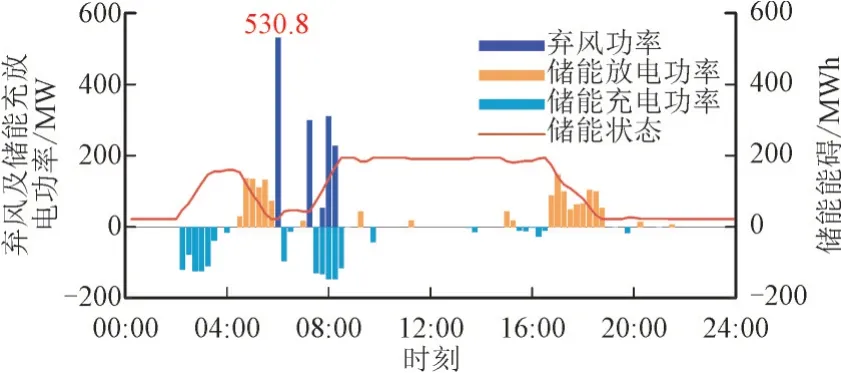
图6 系统加入储能后弃风、储能状态和充放电情况Fig.6 Wind abandonment，energy storage status and charging and discharging status of system after integrating energy storage

此时，优化得到需要配置的最小储能功率为146.505 MW，储能能量为197 MWh。由图6 可知，在配置储能后，系统无失负荷现象发生，且峰时储能释放的电能可在弃风时进行补充，从而减少了弃风电量，此时系统全天的弃风电量为355.3 MWh。综合考虑火电成本、风电成本、弃风成本及储能成本，此时系统的单位供电0.016 8 万元/MWh。

对比场景3 和场景4，储能配置方案的相关指标统计如表4 所示。

表4 高比例风电场景下系统相关指标统计Table 4 Statistics of system indicators under different scenarios with wind power penetration

由表4 可以看出，在600 MW 风电替代时，通过Cplex 求解器仿真分析可得保证不失负荷失时，场景5 中储能投资及运维成本年平均成本为37.9 万元，远低于场景4 的失负荷成本（173 万元）。相比于场景3 和场景4，当采用配置储能的方式来保证不失负荷时，高比例风电替代的电力系统单位供电成本显著降低。因此，当风电替代比例越大时，采用配置储能以保证供电可靠性更加经济。

3.3 长时间尺度下储能方案经济性优势分析

大容量风电接入将对系统的经济性及可靠性产生较大影响，有必要寻找合理的功率平衡解决方案十分必要，由于失负荷成本较高，达到8 元/kWh，因此在功率平衡时应尽量以不失负荷为基本原则，进而保障系统运行的可靠性和经济性。基于该原则，可以通过增加风电装机、配置储能来进行功率平衡，下面分析采用配置储能方案的经济性。

增加配套储能且保障系统不失负荷时，此时的目标函数与约束条件与2.3 节所述相同，得到此时系统需增加的储能功率为826.88 MW，储能能量为18 922 MWh，系统各机组出力和弃风情况如图7 和图8 所示。

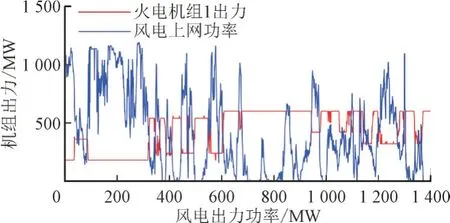
图7 增加储能保证不失负荷时的机组出力Fig.7 Unit out without lost load when integrating energy storage

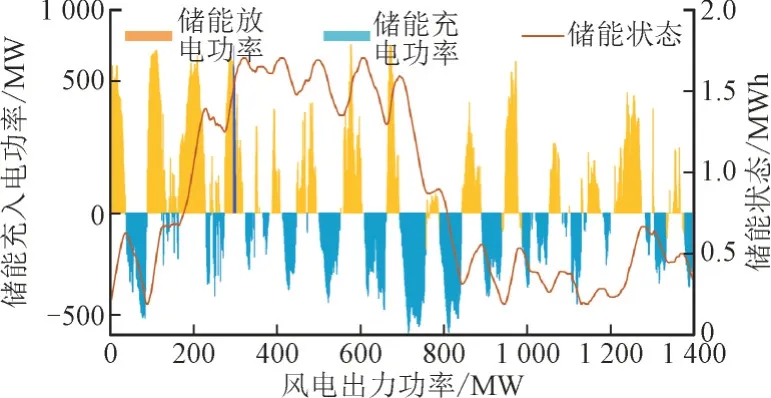
图8 增加储能不失负荷时系统储能状态和充放电功率Fig.8 Energy storage state and charge and discharge power of system without lost load when integrating energy storage

由图7 和图2 可知，在不失负荷的前提下，增加储能容量后的单位供电成本为0.192 元/kWh。原因在于保障某些时段的负荷功率需求，导致其他负荷需求不高的时段产生较大的弃风电量，进而导致单位供电成本上升。因此，在风电渗透率较高时，增设储能设备保证可靠供电的经济性更好。然而，此时的储能装设容量达到较高，在实际工业中无法实现如此大容量的储能设备。

4 结语

高比例风电渗透是未来新型电力系统发展的必然趋势，但高比例风电渗透使电力系统的供电可靠性和调节能力下降，严重威胁电力系统运行的安全稳定，进而导致电力系统的单位运行成本急剧增加。对于含高比例风电电力系统，根据实际电源系统组成及日负荷曲线来合理优化容量储能设备的容量，不仅能增加风电消纳空间以降低单位供电成本，而且能避免系统出现失负荷情况发生而保证电力系统的安全可靠性。