变结构交互式多模型滤波和平滑算法

陈维义, 何 凡,*, 刘国强, 毛伟伟

(1. 海军工程大学兵器工程学院, 湖北 武汉 430030; 2. 海军士官学校兵器系, 安徽 蚌埠 233000)

0 引 言

目前,卡尔曼滤波、粒子滤波、基于机器学习的滤波及其改进形式已被广泛应用在目标跟踪、参数估计和状态预测等领域[1-4]。对于基于单模型的滤波方法而言,当目标机动十分复杂时,会出现滤波模型与目标机动模型不匹配的情况,从而导致滤波精度大幅降低[5]。

针对这一问题,交互式多模型(interacting multiple model, IMM)[6-8]展现出更加优越的性能。近些年,IMM算法得到了很多学者的关注,很多学者在结构和参数等层面对IMM算法进行了改进。文献[9]基于恒速和当前统计模型设计了IMM算法,首先利用最小二乘法估计当前统计模型的平均速度,然后将当前统计模型应用于IMM算法。该方法提高了模型精度,从而提高了滤波精度。文献[10]从多个方面对IMM算法进行了改进,包括采用改进的卡尔曼滤波器作为子滤波器、不同模型之间的非对称状态估计和基于熵的模型概率更新公式。文献[7,11]提出了IMM的一种替代方法,模型集中的模型由匀加速模型构成,降低了模型集的复杂程度。在此基础上,文献[12]提出了一种自适应IMM算法,首先利用滤波器对目标的加速度进行估计,然后选取估计加速度附近的值构建模型。该方法可以减少模型集中模型的数量,在降低计算量的同时提高了模型精度。文献[13]基于二阶马尔可夫链提出了一种二阶IMM算法,该算法利用了更多的先验信息,提高了滤波精度。由于上述IMM模型集中的模型种类和数量不变,所以又称其为固定结构IMM(fixed structure IMM, FSIMM)。

为了避免因模型不匹配而造成的精度误差问题,在使用IMM算法时,应使用尽可能多的模型覆盖目标机动模型。但值得注意的是,单个模型集中模型过多,同样会降低滤波精度[14]。在此背景下,变结构IMM(variable structure IMM,VSIMM)应运而生。VSIMM经过不断的发展和改进,大致可以分为4类:模型组切换(model group switching, MGS)、可能模型集(likely mode set, LMS)、期望模型增强(expected mode augmentation, EMA)和自适应网格(adaptive grid,AG)[15]。其中,MGS将模型集分为模型子集,一个时间步长只选择一个模型子集进行估计,模型子集之间根据模型子集转移概率进行切换[16]。LMS将模型分为3种类型:不可能的、重要的和主要的模型,在每个时间步长里,用于估计的模型子集由主要的模型和接近主要的模型构成[17-18]。与MGS类似,EMA将一个大的模型集分成小的模型子集,然后计算下一个时间步长所有模型子集的概率,选择概率最大的模型子集用于估计[19]。AG算法结合图理论,将所有的模型构成一个网格,利用先验信息和当前数据得到一个局部细化网格,细化网格中的模型构成候选模型子集,然后根据规则选择模型,构成下一时刻用于滤波的模型子集[20]。

值得注意的是,文献[19]所提到的EMA方法在计算似然函数和模型子集概率时,对公式进行了近似。针对这一问题,本文首先设计了一种新的VSIMM(novel VSIMM, NVSIMM)滤波算法,给出了精确的数学模型。另外,在前向NVSIMM滤波的基础上,对数据进行平滑处理,设计了VSIMM平滑(VSIMM smoothing, VSIMMS)算法,前向NVSIMM和后向VSIMMS相结合即为VSIMM滤波和平滑(VSIMM filtering and smoothing, VSIMMFS)算法。

本文安排如下:第1节对滤波和平滑问题进行了描述,并给出了IMM滤波算法和IMM平滑算法的数学模型;第2节设计了VSIMMFS算法,包括前向NVSIMM滤波和后向VSIMM平滑两个部分;第3节对本文所提算法的有效性进行仿真验证和讨论;最后,第4节给出了本文的结论。

1 IMM滤波和平滑算法

1.1 问题描述

假设目标可能有r个运动模型,模型集记为Ω={M1,M2,…,Mr},模型之间的转换概率矩阵为

(1)

式中:pij(1≤i≤r,1≤j≤r)为模型i到模型j的转移概率。

系统离散化状态方程如下:

(2)

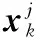
模型j的量测方程为

(3)

1.2 前向IMM滤波

IMM算法框图如图1所示。

图1 IMM算法框图Fig.1 Block diagram of the IMM algorithm

IMM算法一般可以分为以下4个步骤[6-7]。

步骤 1前向输入交互

(4)

(5)

(6)

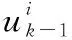
步骤 2滤波

分别基于每一个模型进行卡尔曼滤波:

步骤 2.1预测状态

(7)

步骤 2.2预测协方差矩阵

(8)

步骤 2.3计算卡尔曼增益

(9)

步骤 2.4滤波估计

(10)

步骤 2.5滤波值的协方差

(11)

步骤 3模型概率更新

模型概率更新公式为

(12)

(13)

(14)

步骤 4输出

IMM滤波的状态估计和协方差估计分别为

(15)

(16)

1.3 后向IMM平滑

在前向IMM滤波的基础上,对数据进一步进行平滑处理,得到后向IMM平滑算法,其算法框图如图2所示,包括以下几个步骤[21]。

步骤 1后向状态交互

后向混合状态和对应的协方差为

(17)

(18)

(19)

(20)

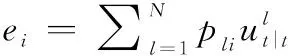
步骤 2卡尔曼平滑[22]

平滑值和对应的协方差为

(21)

(22)

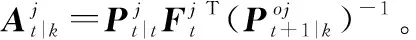
步骤 3平滑模型概率更新

平滑后的模型概率计算公式为

(23)

步骤 4IMM平滑状态交互

后向IMM平滑的状态输出和对应的协方差为

(24)

(25)

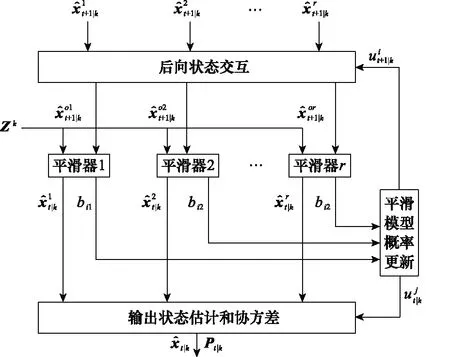
图2 IMM平滑算法框图Fig.2 Block diagram of the IMM smoothing algorithm

2 VSIMMFS算法

VSIMMFS算法包括前向NVSIMM滤波和后向VSIMM平滑两个部分,这两个部分分别在后续两个小节中展开。

2.1 VSIMM滤波

为了避免模型集中模型数量过多,减少模型误差,本节设计了NVSIMM算法。NVSIMM滤波算法包括多个模型子集,每个模型子集独立运行IMM,选取概率最高的模型子集的估计结果作为最终的估计状态输出。NVSIMM算法框图如图3所示。

图3 NVSIMM算法框图Fig.3 Block diagram of NVSIMM algorithm

算法包括以下4个步骤。

步骤 1并行独立IMM状态估计

步骤 2计算每个模型子集的似然函数

模型子集的似然函数为

(26)

(27)

步骤 3计算模型子集概率

记模型子集概率p(Πk(m)|Zk)=κk(n),则有:

(28)

式中:p(zk|Zk-1,Πk(n))在步骤2中已经求出,分母为归一化因子,p(Πk(n)|Zk-1)根据全概率公式有:

(29)

式中:κk-1(m)=p(Πk-1(m)|Zk-1)为上一时刻的模型子集概率,应用马尔可夫性质可知模型子集转移概率与观测值无关,即:

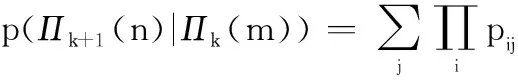
(30)

步骤 4NVSIMM滤波状态估计

选择概率最大的模型子集的IMM估计结果作为最终的状态估计输出,首先求出概率最高的模型子集编号:

(31)

从而可以得到最终的状态估计和对应的协方差为

(32)

Pk|k=Pk|k(nm)

(33)

2.2 VSIMMS算法

本节在NVSIMM的基础上,对数据进行进一步平滑,得到VSIMMS算法。VSIMMS算法框图如图4所示。

图4 VSIMMS算法框图Fig.4 Block diagram of VSIMMS algorithm

算法包括以下4个步骤。

步骤 1并行独立IMM状态平滑

步骤 2计算平滑后的模型子集的似然函数

应用全概率公式和马尔可夫性质,可以得到模型子集的似然函数为

(34)

式中:p(zk|Zk-1,Πk(m))为前向NVSIMM滤波过程中模型子集的似然函数,应用全概率公式和马尔可夫性质,p(Πk(m)|Πt(n))可以转化为

(35)

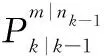
(36)

(37)

步骤 3计算平滑后的模型子集概率

根据贝叶斯定理可以得到模型子集概率为

(38)

(39)

步骤 4VSIMMS状态估计

概率最高的模型子集编号为

(40)

判断概率最高的模型子集在Tswitch时间段内是否发生变化。若发生变化,VSIMMS的状态估计和对应的协方差为

(41)

Pt|k=Pt|k(Ω)

(42)

若不发生变化,VSIMMS的状态估计和对应的协方差为

(43)

(44)

3 仿真与讨论

为了验证VSIMMFS算法的有效性,本节首先针对三维空间中的目标运动轨迹展开分析讨论。目标的初始位置、速度和加速度分别为(10 km, 40 km, 30 km)、(300 m/s, 0, 0)和(0, 0, 0)。目标的机动参数如下:

(1) 30 s的匀速直线运动;

(2) 30 s的匀加速运动,加速度大小为(-10 m/s2, -10 m/s2, -10 m/s2);

(3) 30 s的匀速转弯运动,转弯角速率为(0.2 rad/s, 0.2 rad/s, 0);

(4) 30 s的匀速直线运动。

目标运动轨迹如图5所示。

图5 目标运动轨迹Fig.5 Target motion trajectory

利用蒙特卡罗法分析对比IMM、NVSIMM和VSIMMFS的性能,其中IMM算法包括3个模型:匀速直线运动(constant velocity, CV)模型、匀加速运动(constant acceleration, CA)模型和匀速转弯(constant turn, CT)模型[23-25]。VSIMMFS算法包括两个模型子集,第一个模型子集包括CV、CA,第二个模型子集包括CV、CT;NVSIMM滤波算法包括的模型子集和VSIMM相同。可以注意到,VSIMMFS和NVSIMM仅需两个原始模型子集即可包括所有的模型,但这两种算法的原始模型子集并不包括模型子集CA、CT。设模型转移概率矩阵为

假设系统过程噪声的标准差为1 m/s2,测量噪声的标准差为50 m,Tswitch=20 s,仿真结果如图6～图9所示。图6给出了IMM算法中模型概率变化曲线,其中,概率最大的曲线所对应的模型与目标实际机动模型相同。图7给出了NVSIMM和VSIMMFS中模型子集概率曲线,由图7 可知,平滑后(VSIMMFS)的模型子集概率大于NVSIMM的模型子集概率,说明平滑后的模型子集与目标机动模型匹配程度更高。另外,对比图6和图7可知,图6中概率最大的曲线所对应的模型属于图7中概率高的模型子集,也就是说,概率最高的模型子集始终包括目标实际的机动模型。图8给出了IMM、NVSIMM和VSIMMFS对目标运动轨迹的跟踪效果,这3种方法都能够对目标轨迹进行较好的估计,三者之间的差异具体体现在图9中。图9给出了IMM、NVSIMM和VSIMMFS对目标位置估计的均方根误差(root mean square error, RMSE)曲线。从图9中可以看出,VSIMMFS的RMSE最小,VSIMMFS次之,IMM的RMSE最大。值得注意的是,概率最大的模型子集发生变化时,NVSIMM算法的性能会短暂下降,而VSIMMFS算法对位置估计的RMSE与IMM相同,原因在于在设计VSIMMFS算法时,当最大概率的模型子集短暂发生时,利用基于模型全集的IMM估计值作为VSIMMFS的估计值,从而避免了VSIMMFS算法短暂的性能下降。

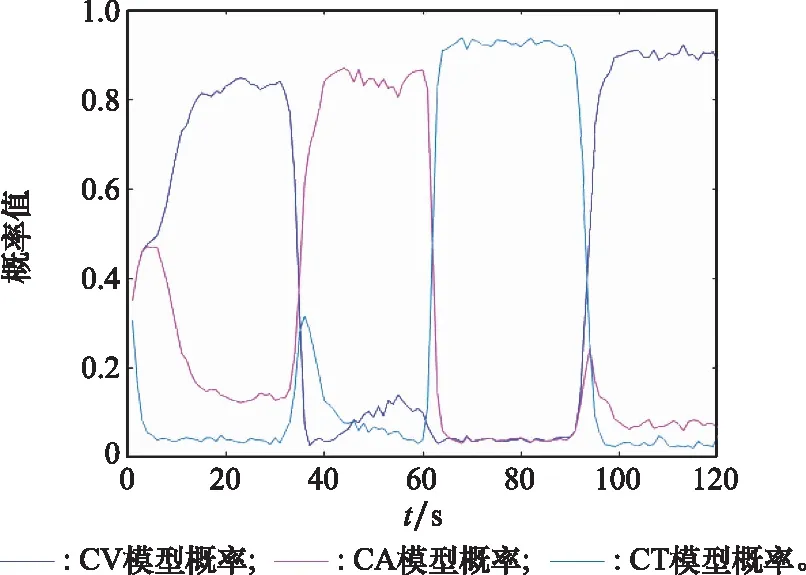
图6 IMM算法中的模型概率Fig.6 Model probability in IMM algorithm

图7 NVSIMM和VSIMMFS中模型子集概率Fig.7 Model subset probabilities in NVSIMM and VSIMMFS

图8 目标运动轨迹跟踪效果Fig.8 Effect of target trajectory tracking

图9 位置跟踪的RMSEFig.9 RMSE of position tracking

为了进一步体现VSIMMFS算法的优越性,将VSIMMFS与基于深度强化学习的目标跟踪算法(maneuvering target tracking based on deep reinforcement learning, MTTDRL)[27]、粒子滤波(particle filter, PF)[28]、基于粒子群优化的PF(particle swarm optimization algorithm-based PF, PSO-PF)[29]、基于混沌PSO-PF(chaos PSO-PF, CPSO-PF)[26,30]进行对比。为了保证对比的有效性,仿真参数参考文献[26]和文献[27]设计,目标的运动轨迹如图10所示。图11分析对比了上述算法对目标位置的跟踪性能。由图11(a)可知,相比于PF、PSO-PF和CPSO-PF,VSIMMFS的位置跟踪的RMSE较小;从图11(b)可以看出,利用VSIMMFS对目标跟踪时的位置偏差更小。所以综上可知,VSIMMFS的跟踪性能优于上述其他算法。

图10 目标运动轨迹Fig.10 Target motion trajectory

图11 算法性能对比Fig.11 Performance comparison of algorithms

4 结 论

为了进一步提高对机动目标的跟踪精度,本文设计了一种VSIMMFS算法。该方法包括前向VSIMM滤波和后向VSIMMS两个部分,通过并行独立运行IMM滤波和IMM平滑,选择概率最大的模型子集的估计结果作为最终的状态估计值。通过与IMM、NVSIMM、PF、PSO-PF、CPSO-PF和MTTDRL算法比较,VSIMMFS具有更好的跟踪性能。