时域离散类主瓣干扰下基于样本识别的雷达和差测角方法

周必雷, 李荣锋, 陈 辉, 陈 浩, 戴凌燕,刘维建, 李槟槟

(1. 空军预警学院, 湖北 武汉 430019; 2. 航天南湖电子信息技术股份有限公司, 湖北 荆州 434000)

0 引 言

空天防御是国家战略力量的组成,已成为新时期军事强国的重要标志。弹道导弹在突防时除了施放诱饵弹头,往往还会施放多个弹载干扰机。这些弹载干扰机与弹头长时间伴飞,处于雷达的同一个波束内,可形成主瓣干扰,对雷达构成严重威胁。

十多年来,雷达抗干扰技术取得了长足进步,旁瓣对消、旁瓣匿影、参数捷变等抗干扰措施的综合运用有效提高了雷达抗干扰能力。但是,这些措施可以有效对抗副瓣干扰,而对主瓣干扰却很难奏效。主瓣干扰按照干扰效果进行分类,可以分为压制类和欺骗类。压制类主瓣干扰在时域上表现为全距离段覆盖,时域上是连续的。而欺骗类主瓣干扰在时域上表现为非全覆盖,如切片转发干扰、密集假目标干扰、灵巧类干扰等,在时域上是离散的。

自适应数字波束形成(adaptive digital beam forming, ADBF)技术[1]是一种目前已经被成熟运用的抗干扰技术,但是在抑制主瓣干扰后存在波束指向偏移、主瓣畸变和目标输出信噪比(signal to noise ratio, SNR)损失严重等问题。针对主瓣畸变问题,李荣锋等[2-3]提出了主瓣干扰条件下基于阻塞矩阵预处理和特征投影预处理的自适应方向图保形方法。1984年,Applebaum等[4]提出了主瓣干扰对消(mainlobe jamming cancellation, MLC)[4]方法,这是一种比较经典的主瓣干扰对消方法,其中心思想是将和波束作为主通道、差波束作为辅助通道进行主瓣干扰对消。Yu等[5]于2005年在其专利[5]中提出联合应用ADBF与MLC技术,由此增加干扰抑制的自由度,可以分步抑制主、副瓣干扰。上述工作只涉及主瓣干扰抑制问题,并未涉及目标到达角(direction of arrival, DOA)估计。

针对主瓣干扰抑制后的DOA估计问题,目前较为经典且应用较为普遍的是单脉冲测角法,其中心思想是在主瓣干扰抑制后保证和、差主瓣不畸变,可以归纳为约束类[6-9]和分维类[10-17]。约束类方法是对自适应单脉冲曲线施加约束点,使其拟合静态单脉冲曲线[6-8],从而有效进行DOA估计,文献[9]在文献[6-8]的基础上利用罚函数增加了低副瓣约束。但是这类方法在主瓣干扰附近的目标DOA估计精度较低。分维类方法的中心思想是在某一维空域上进行主瓣干扰对消,且保证另一维空域上能够有效进行DOA估计,这类方法对阵列天线有要求,要求阵列天线必须为面阵,目前较为经典的是和差四通道算法[10]及其扩展算法[11-17]。这类方法利用某一维空域上的和、差波束对消主瓣干扰,同时不影响另一维空域上的和、差波束测角。近几年,Chen等[13]和Yu等[14]在文献[10]思想的基础上又提出了一种新的思路,其中心思想是在某一维上采用ADBF进行主瓣干扰抑制,同时可以保证另外一维上目标的角度参数信息,进而利用单脉冲技术进行测角。然而,上述方法有效的前提是采集的干扰样本必须足够纯净,能够构造出准确的干扰子空间,以保证干扰抑制效果。

针对时域离散类主瓣干扰而言,若对其进行固定距离单元采样或全程采样,均不能够得到纯净的干扰样本,这将导致所构造的干扰协方差矩阵严重失真,致使干扰抑制空域零深变浅,无法有效抑制干扰,直接影响测距、测角。对此,本文提出了一种时域离散类主瓣干扰下基于样本识别的雷达和差测角方法。所提方法利用了信源(目标和干扰)在和、差通道的相关性差异,基于此提取纯净的干扰训练样本,然后利用空域方位维、俯仰维的正交性进行主瓣干扰抑制,同时估计目标角度。

1 阵列接收信号模型

采用N1行N2列等距均匀矩形面阵,阵元间距为d,阵列波束指向为(θb,φb),前者为方位角,后者为俯仰角。雷达发射信号波长为λ。电磁环境中存在一个目标s0(k)和一个主瓣干扰s1(k),分别位于(θ0,φ0)、(θ1,φ1)。阵列接收数据可表示为

x(k)=As(k)+n(k)

(1)

式中:k表示时域采样序号;A=[a(θ0,φ0),a(θ1,φ1)]为阵列流形矩阵;s(k)=[s0(k),s1(k)]T;n(k)为N1N2×1维阵元噪声矢量;a(θi,φi)=a(φi)⊗a(θi);⊗为Kronecker积;a(φi)=[1,e-jαi,…,e-j(N1-1)αi];a(θi)=[1,e-jβi,…,e-j(N2-1)βi];θi表示第i个信源的方位角;φi表示第i个信源的俯仰角;αi=2πdsinφi/λ;βi=2πdcosθicosφi/λ。

2 算法原理

干扰对消效果的优劣在很大程度上取决于干扰样本采样的准确度。由于常规的自适应处理对于干扰采样是固定的,这就导致了有可能出现学习不到干扰样本或者学到的样本不纯的问题,从而导致算法性能失效。而时域离散类主瓣干扰在时域上处于离散状态,按照常规的固定距离采样显然无法采集到纯净的样本。因此,本文在干扰抑制前增加一个干扰样本选择系统,提高干扰样本学习的纯净度,从而提高干扰抑制的稳健性。整体算法流程如图1所示。

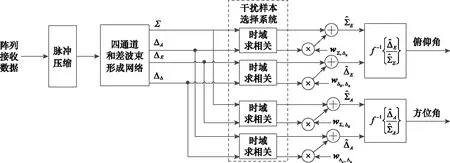
图1 所提方法示意图Fig.1 Schematic diagram of the proposed method

所提方法主要分为以下4个步骤。

步骤 1对阵列接收信号进行脉压处理以提高信源(目标与假目标)SNR,再将其送入四通道和差波束形成网络。和波束低副瓣权值通常采用泰勒权或切比雪夫权,差波束低副瓣权通常采用贝里斯权。在方位维和俯仰维均加“和权”得到和波束Σ,在方位维加“差权”及俯仰维加“和权”得到方位差波束ΔA、在方位维加“和权”及俯仰维加“差权”得到俯仰向差波束ΔE,在方位维和俯仰维均加“差权”得到双差波束ΔΔ。上述4个波束对应的时域输出可以分别表示为xΣ(k)、xΔA(k)、xΔE(k)、xΔΔ(k)。

步骤 2求和通道输出xΣ(k)与方位差通道输出xΔA(k)的时域相关系数。针对制导/火控雷达而言,当雷达跟踪上目标时,其主波束指向基本靠近目标,故和通道内既有目标也有干扰,而差通道内目标能量几近为零,干扰能量较大。因此,xΣ(k)与xΔA(k)的时域相关系数较大值位于密集假目标干扰所在距离单元。基于此结论,设置相关系数门限值为Λ,进而采集得到纯净的干扰训练样本。

假设ρΣ,ΔA(i)表示xΣ(k)与xΔA(k)的相关系数:

(2)

同理,可以求得俯仰差通道输出xΔE(k)与双差通道输出xΔΔ(k)的相关系数ρΔE,ΔΔ,和通道输出xΣ(k)与俯仰差通道输出xΔE(k)的相关系数ρΣ,ΔE,方位差通道输出xΔA(k)与双差通道输出xΔΔ(k)的相关系数ρΔA,ΔΔ。再依据干扰样本判别门限Λ,可以分别得到对应的干扰样本所在距离单位为iΔE,ΔΔ、iΣ,ΔE、iΔA,ΔΔ。

步骤 3根据选取的干扰样本进行自适应干扰抑制处理。

(3)

式中:

(4)

(5)

(6)

式中:

(7)

(8)

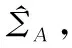
(9)

式中:

(10)

(11)

(12)

式中:

(13)

(14)

步骤 4依据方位维和俯仰维的空域正交性进行和差测角。

式(4)可以重新表示为

(15)

式中:gΔA表示方位差波束ΔA在干扰方向的增益;PJ为干扰功率;PN为噪声功率,显然PJ远大于PN。因此,式(15)近似可得

(16)

式(5)可以重新表示为

(17)

式中:gΣ表示和波束Σ在干扰方向的增益。

因此,式(3)可以重新表示为

(18)

式中:gΣa和gΣe分别表示和波束Σ在干扰方向的方位维增益和俯仰维增益;gΔa表示方位差波束ΔA在干扰方向的方位维增益。

按照相同的步骤,可以得到

(19)

式中:gΔΔ表示双差波束ΔΔ在干扰方向的增益。

(20)

式中:gΔE表示俯仰差波束ΔE在干扰方向的增益。

因此,式(6)可以表示为

(21)

式中:gΔe表示双差波束ΔΔ在干扰方向的俯仰维增益。

根据式(18)和式(19)的结果可知

wΣ,ΔA=wΔE,ΔΔ

(22)

(23)

(24)

式(24)可化简为

(25)

同理,可以得到方位维自适应单脉冲比:

(26)

3 仿真实验与性能分析

3.1 仿真实验

考虑等距均匀面阵,仿真参数设置如表1所示。阵列通道采用和差四通道,即和通道、方位差通道、俯仰差通道、双差通道。

表1 仿真参数设置

图2和图3分别给出了和通道的时域输出与脉压输出结果,可见7个疑似目标,无法判别真实目标所在位置。

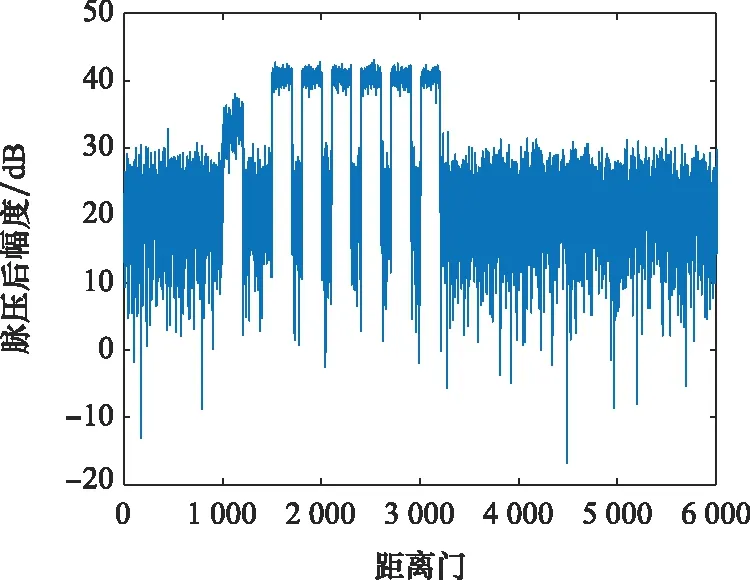
图2 和波束时域输出图Fig.2 Output of the sum beam

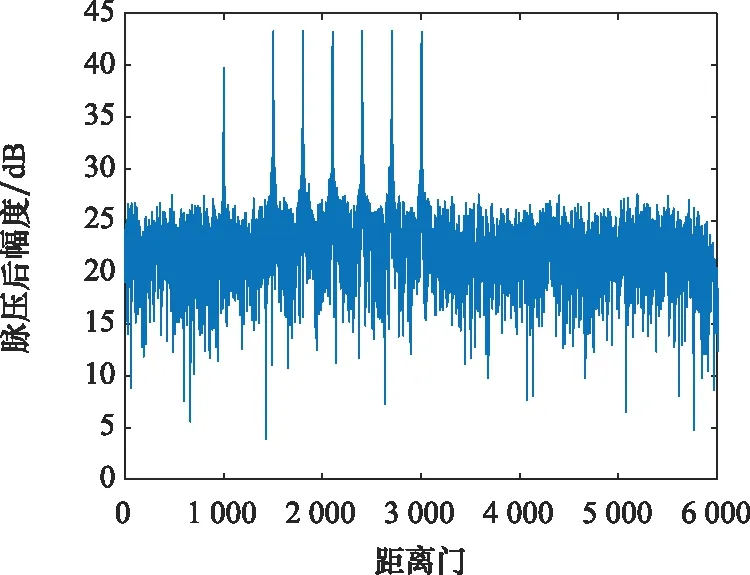
图3 和通道时域脉压输出图Fig.3 Output of the sum beam with time-domain pulse compression

图4和图5分别给出了全距离单元采样下的自适应方位和波束图与自适应俯仰和波束图,可见方向图在主瓣干扰所在位置的零深分别为-19.9 dB与-20.5 dB。图6和图7分别给出了全距离单元采样下的自适应俯仰和波束输出与自适应方位和波束输出,可见干扰未能全部抑制,仍然无法通过鉴别得到真实目标。

图4 自适应方位和波束图(全距离单元采样)Fig.4 Adaptive azimuth sum beam pattern with full range sampling

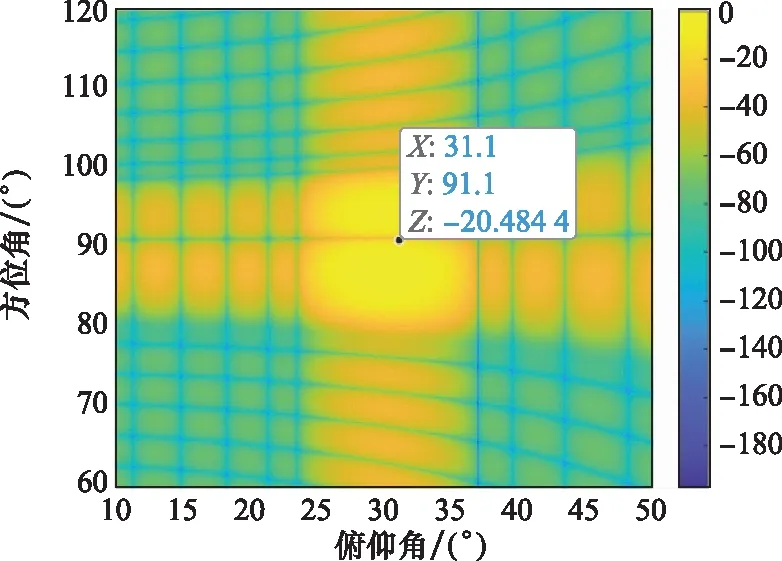
图5 自适应俯仰和波束图(全距离单元采样)Fig.5 Adaptive elevation sum beam pattern with full range sampling

图6 自适应俯仰和波束输出图(全距离门采样)Fig.6 Output of the adaptive elevation sum beam with full range sampling

图7 自适应方位和波束输出图(全距离门采样)Fig.7 Output of the adaptive azimuth sum beam with full range sampling

图8～图11分别给出了和差四通道两两间的相关系数,可见图中大值所在的距离单元与干扰所在距离单元一致。

图8 和通道与方位差通道相关系数Fig.8 Correlation coefficient between sum channel and azimuth difference channel

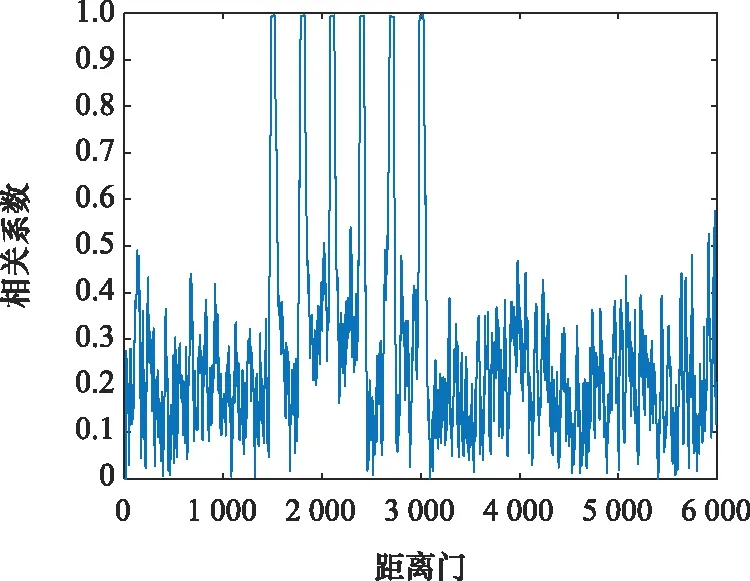
图9 和通道与俯仰差通道相关系数Fig.9 Correlation coefficient between sum channel and elevation difference channel

图10 方位差通道与双差通道相关系数Fig.10 Correlation coefficient between azimuth difference channel and double difference channel

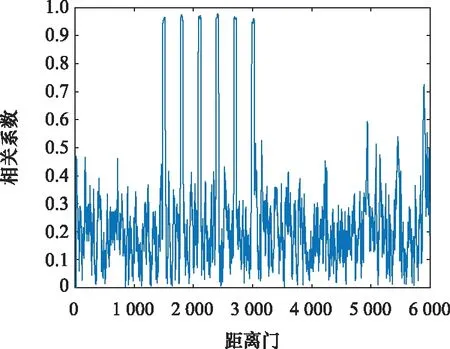
图11 俯仰差通道与双差通道相关系数Fig.11 Correlation coefficient between elevation difference channel and double difference channel

图12和图13分别给出了依据相关性进行采样后得到的自适应方位和波束图与自适应俯仰和波束图,可见干扰零深分别为38.8 dB与43 dB。对比图4和图5可以看出,零深明显加深。

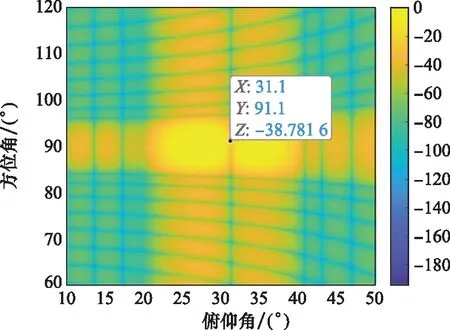
图12 自适应方位和波束图(所提方法)Fig.12 Adaptive azimuth sum beam pattern with the proposed method

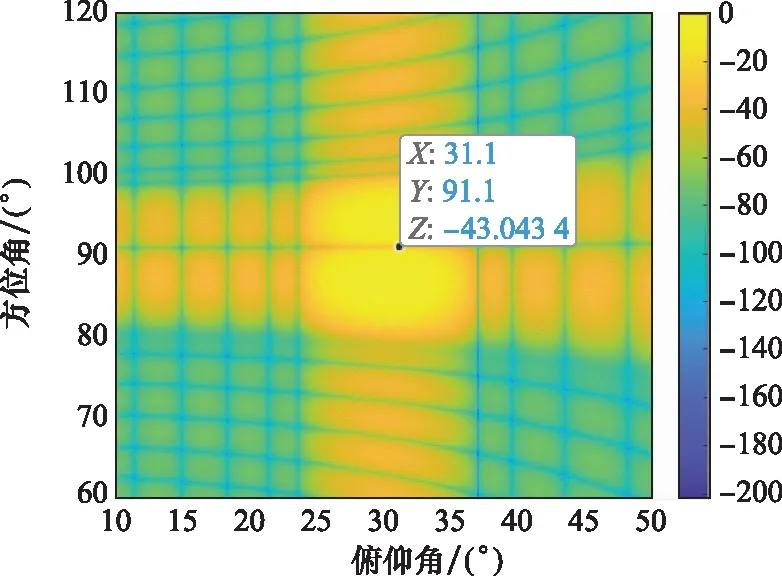
图13 自适应俯仰和波束图(所提方法)Fig.13 Adaptive elevation sum beam pattern with the proposed method

图14和图15分别给出了依据相关性进行采样的自适应俯仰和波束输出与自适应方位和波束输出,可见在第1 000距离单元处发现目标,与仿真设置一致。

需要指出的是,根据图8～图11分别给出的和差四通道两两间的相关系数可知,对应的干扰所在距离单元是一致的。因此,可选择求解其中一路的相关性系数即可,由此可降低一定的运算量。

图14 自适应俯仰和波束输出图(所提方法)Fig.14 The output of the adaptive elevation sum beam with the proposed method

图15 自适应方位和波束输出图(所提方法)Fig.15 The output of the adaptive azimuth sum beam with the proposed method

3.2 性能分析

图16和图17分别给出了方位向及俯仰向的和差单脉冲曲线,可见自适应后的单脉冲曲线很好地拟合了静态单脉冲曲线,即干扰抑制后并不影响单脉冲测角。

图16 方位向单脉冲曲线Fig.16 Azimuth monopulse curve

图17 俯仰向单脉冲曲线Fig.17 Elevation monopulse curve

固定目标输入SNR为20 dB(脉压及空域合成后),目标俯仰角为30°。图18给出了目标方位角变化时的测角精度曲线,以均方根误差(root meah square error,RMSE)描述,可见目标方位角RMSE小于0.6°,约为1/5波束宽度,当目标接近主波束指向时,目标方位角RMSE约为0.3°,即1/10波束宽度;固定输入目标SNR为20 dB(脉压及空域合成后),目标方位角为90°,图19给出了目标俯仰角变化时的测角精度曲线,可见目标俯仰角RMSE小于0.65°,约1/5波束宽度。当目标接近主波束指向时,目标俯仰角RMSE约为0.4°,即1/8波束宽度。

图18 目标方位向测角RMSE(SNR为20 dB)Fig.18 Target azimuth angle measurement RMSE (SNR=20 dB)

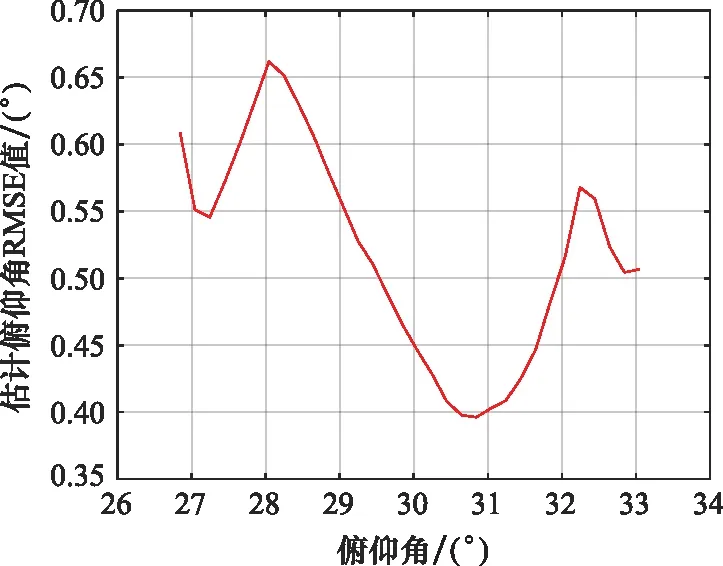
图19 目标俯仰向测角RMSE(SNR为20 dB)Fig.19 Target elevation angle measurement RMSE (SNR=20 dB)

图20给出了所提方法测角精度随目标SNR变化的结果,其中图20(a)为目标方位角估计RMSE曲线,图20(b)为目标俯仰角估计RMSE曲线。由图可见,测角精度随着目标SNR的提高而提高。在SNR较低时,如SNR为12 dB时,方位及俯仰测角精度均约为1.3°,即约为2/5波束宽度。

图20 目标角估计RMSE随目标SNR的变化曲线Fig.20 Target angle estimation RMSE change curve via SNR

4 结束语

针对时域离散类主瓣干扰样本采集不纯导致干扰抑制能力以及和差测角能力严重下降的问题,本文提出一种新的基于样本识别的雷达和差测角方法。该方法利用了目标与主瓣干扰在和通道、差通道时域相关性的差异性,依据此提取纯净的干扰样本来提高干扰噪声协方差矩阵的准确度,进一步提升主瓣干扰抑制能力与和差测角精度。理论推导和仿真实验表明,所提方法在时域离散类主瓣干扰背景下可有效提取干扰样本,从而具备较好的雷达测角能力。