基于混合遗传算法的海军航空兵场站物资配送车辆调度智能优化

阎 哲, 汪民乐, 汪江鹏, 闫少强, 吴丰轩

(火箭军工程大学基础部, 陕西 西安 710025)

0 引 言

海空航空兵战机执行飞行任务,需要海空航空兵场站提供雷弹、航空器材、附属油料等物资供应保障。日常状态下,各类物资分别存储在相应的配送中心,在战机飞行准备阶段,场站根据任务需求派遣车辆,将其送至指定位置。传统的配送模式主要依靠调度人员的工作经验,对配送车辆和物资的配送顺序进行简单筹划,甚至只告知驾驶员总体的配送需求,由驾驶员自己规划配送路线。随着海军航空兵改革转型和任务拓展进一步深入,“多机种”“大批量”飞行保障任务已成常态,继续沿用传统的配送模式,不仅会造成保障资源的浪费,限制场站飞行保障能力的发挥,严重时还会影响战机飞行,所以亟需使用更加科学、高效的方法对物资配送问题进行研究。

海军航空兵场站物资配送问题的关键就是配送车辆调度优化。针对车辆调度优化问题约束要素多、数据规模庞大等特点,许多学者引入智能优化算法对该问题进行研究,并取得了不少成果[1-16]。其中,遗传算法(genetic algorithm, GA)因其思想比较简单、容易实现且算法特性健壮等优点,被广泛应用[17]。但应对愈发复杂的车辆调度优化系统,经典GA迭代时间长、容易陷入局部最优的缺点就越发凸显。因此,提高算法收敛性能、预防其早熟成为了研究热点。文献[18-22]分别从动态调整交叉和变异概率、引入差分变异与粒子群算法的更新规则、采用精英选择机制等对GA进行了改进,均取得了不错的效果,对解决海军航空兵场站物资配送车辆调度优化问题有很大的借鉴意义。

本文针对海军航空兵场站物资配送问题,建立了物资配送车辆调度优化模型,在经典GA的基础上引入模拟退火(simulated annealing, SA)算法,提出了混合GA(hybrid GA, HGA)用于求解该模型,实现物资配送车辆调度的智能优化。仿真实验表明,与经典GA相比,HGA取得了更为满意的优化结果。

1 问题描述

海军航空兵场站雷弹、航空器材、附属油料分别储备在相应的配送中心,场站保障人员在战机地面准备阶段将其送至工作点位。因为不同种类的物资由不同保障车辆配送,且相互之间影响较小,所以可把多种物资配送问题简化成配送一种物资问题来进行研究。

海军航空兵场站雷弹、航空器材、附属油料等各种物资的配送问题可以描述为:有N架战机,分别停在不同停机位上进行地面准备工作,第i架战机需要场站配送数量为Xi的物资,有M辆车可用于配送作业。场站保障指挥中心统筹所有战机的物资需求,制定详细的配送方案,明确保障车辆的出车数量、出车时间和配送顺序,在规定时间内完成配送任务的基础上,做到保障车辆总数最少且所有保障车辆行驶的距离总和最小,达到提高保障车辆利用率、节约保障资源的目标。

2 海军航空兵场站物资配送车辆调度优化模型

2.1 基本假设

为了将海军航空兵场站物资配送车辆调度问题抽象为最优化数学模型,建立基本假设如下:

(1) 每架战机的物资需求已知;

(2) 战机和配送中心位置已知,相互之间路径唯一,距离固定;

(3) 保障车辆性能已知,车速和最大载荷固定不变;

(4) 战机单次需求量小于运输车最大载荷,且每架战机必须且只能被一辆车配送一次,不能由多辆车分批输送;

(5) 受领任务前,配送车辆在配送中心待命。受领任务后,配送车辆从配送中心出发,配送完成后返回配送中心;

(6) 卸载物资需要一定时间;

(7) 不考虑天气、人员、机械故障、道路堵塞等其他因素的影响。

2.2 参数定义

物资配送模型参数定义如下:

N:需要被配送物资的战机数量;

i,j:战机编号,也是该战机所在停机位的编号,i,j∈(1,2,…,N),且i≠j,i,j=0时代表配送中心;

M:可参与配送任务的车辆数;

m:配送车辆编号,m∈(1,2,…,M);

Dij:战机i到战机j的距离;

Tij:配送车辆从战机i行驶到战机j所需的时间;

C:车辆固定使用成本;

Cd:车辆单位距离行驶成本;

v:车辆行驶速度;

Z:车辆最大载荷;

Xi:第i架战机的物资需求量,且maxXi≤Z;

P,Q:很大的常数;

xijm:车辆m从战机i行驶到j时为1,否则为0。

2.3 数学模型

在规定时间完成配送任务的基础上,以动用车辆最少、车辆总行驶距离最短为目标建立数学模型如下:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

xijm(Z-Xi-Xj)≥0, ∀i,j∈{1,2,…,N};

∀m∈{1,2,…,M}

(10)

xijm∈{0,1}, ∀i,j∈{1,2,…,N};∀m∈{1,2,…,M}

(11)

(12)

以上模型中,式(1)为目标函数,表示在规定时间内完成配送任务,且动用车辆最少,车辆总行驶路径最短,本质上是总配送成本最低;式(2)表示参与配送的车辆数小于或等于所有物资配送车辆总数;式(3)和式(4)表示每架战机必须且只能接受一辆车的物资配送服务;式(5)表示物资配送车辆从配送中心出发完成任务后再回到配送中心;式(6)表示保障车辆单程物资配送总量不超过其最大载荷;式(7)表示物资配送的时间窗约束;式(8)表示物资配送车辆行驶时间与物资配送距离和车辆行驶速度的关系;式(9)表示物资配送车辆从战机i行驶到战机j的时间约束;式(10)表示车辆当前承载的物资数量不小于下一架战机的需求;式(11)表示xijk的取值是0或1;式(12)表示违反时间窗惩罚,如果物资配送时间超出时间窗约束,就给予一定惩罚。

3 HGA设计

GA由美国Michigan大学Holland教授创立[23-24],提供了一种求解复杂系统优化问题的通用框架。但作为一种新型仿生类随机寻优算法,GA的局部搜索能力较差,解决这个问题的一个有效途径就是将其与传统的基于问题知识的启发式搜索算法相结合构成改进GA[25-26]。

SA算法来源于固体退火原理,是一种基于概率的随机寻优算法。根据Metropolis准则,适应度更优的新个体可直接替代当前个体,否则以一定概率保留当前个体。随着退火过程的进行,温度逐渐降低,非优新个体被接收的概率也随之减小。SA算法因其逐步归零的突跳性,可有效避免陷入局部最优[26],但其收敛速度较慢,运算代价非常大,所以很少被单独使用[27-28]。

HGA基于经典GA“优胜劣汰”的运算机制,引入SA算法非优解的保留策略,让进化得到的子种群和其邻域中的潜在优秀个体再次组合,不仅进一步增强了算法的局部搜索能力,同时还保持了GA自身较强的全局搜索特性。两种算法跳出局部最优的示意图如图1所示。

图1 跳出局部最优Fig.1 Jumping out of local optimum

3.1 编码与解码

编码是将问题转化到遗传空间的过程。为应对不同问题的求解需求,学者们提出了二进制编码、整数编码、自然数编码、矩阵编码等多种编码方式。海军航空兵场站物资配送车辆调度优化问题是基于次序的组合优化,问题解的结构比较特殊,因此选择自然数编码来求解。

假设有N架战机等待物资配送,有M辆车可参与配送任务,构建的染色体长度为N+M-1,染色体编码串可表示为(i11,i12,…,i1a,m1,i21,i22,…,i2b,m2,…,mM-1,im1,im2,…,imc),其中i表示战机编号,a+b+…+c=N,m1,m2,…,mM-1∈(N,M+N-1]均代表配送中心。以10架战机、4辆车为例,编码串可表示为(5,6,12,1,3,4,2,11,9,10,8,13,7)。

解码是编码的逆过程,即将染色体的编码向量映射为满足全部约束条件的可行解的过程。由编码过程可知,任意两个m之间的自然数串代表1辆车的配送路径,所以字符串(5,6,12,1,3,4,2,11,9,10,8,13,7)代表了4辆车的配送路径,如图2所示。

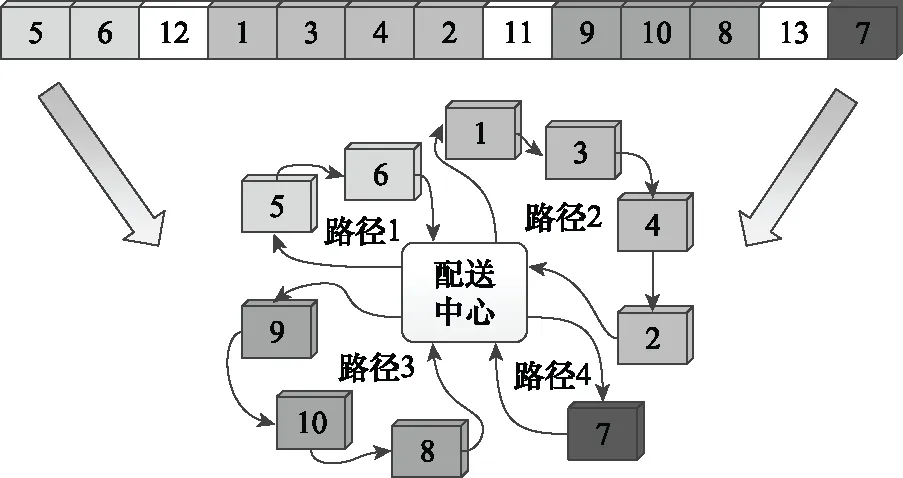
图2 解码过程示意图Fig.2 Schematic diagram of decoding process

第1辆车从保障中心出发,先后为5号、6号战机配送物资再返回;第2辆车从保障中心出发,先后为1号、3号、4号、2号战机配送物资再返回;第3辆车从保障中心出发,先后为9号、10号、8号战机配送物资再返回;第4辆车从保障中心出发,为7号战机配送物资再返回。4条路径共同组成一个完整的物资配送方案。

3.2 初始种群生成

初始种群可以调用randperm函数随机生成,但这样很容易出现劣解,初始种群的质量得不到保证,很有可能影响到算法的效率,因此本文选择类似路径构造的方法来构建初始种群,具体步骤如下。

步骤 1构造一条空路径,随机选择1架未插入的战机作为路径起始点;

步骤 2遍历剩余未插入的战机,选择1架满足载重和时间窗要求的战机插入;

步骤 3重复步骤2,直到没有满足条件的战机为止;

步骤 4重复步骤1～步骤3,直到所有战机均被插入;

步骤 5将上述路径首尾连接生成一条染色体,不同路径间依次使用自然数m1,m2,…,mM-1∈(N,M+N-1]分割,未使用的m放至染色体尾部。

步骤 6将步骤1～步骤5循环NIND次,得到初始种群。

3.3 适应度函数

自然界里的个体是否可以存活下去,取决于其自身适应自然环境的能力,这个能力就是这个个体的适应度。同理,在GA中,一个染色体是否可以遗传下去,也是取决于这个染色体自身的适应度值,适应度值越高,则遗传下去的可能性就越大。本文选取目标函数的倒数作为适用度函数,适应度函数Fit(f(i,j,k))的表达式如下:

(13)

3.4 遗传操作

遗传操作的作用是实现优胜劣汰,让生命力强(即适应度高)的染色体遗传到下一代并进行进化。遗传操作包含3个基本算子,分别是选择算子、交叉算子和变异算子[29]。

3.4.1 选择算子

选择算子是在种群中筛选出可以遗传至下一代的个体,本文选择简单易于实现的轮盘赌选择算子,其基本思路是通过种群中个体染色体适应度值的大小来确定其遗传至下一代的可能性,适应度值越高的个体被选择的可能性越大,适应度值越低的个体被选择的可能性越小。

3.4.2 交叉算子

交叉算子就是将两个父辈个体进行基因重组交换,从而产生适应度更高的子代个体。本文染色体的基因代表是接受配送服务战机的编号,而每架战机必须且只能接受一辆车的物资配送服务。如果对两个父辈个体直接进行交叉操作,则很容易在子代染色体上产生重复基因,这样的子代染色体是无效的。为了避免这种情况的发生,本文选择部分匹配交叉的方式进行交叉操作,即在两点交叉的基础上建立匹配关系,对重复基因进行替换,以消除冲突,得到两条有效染色体。

3.4.3 变异算子

自然界中的基因会受多种因素影响而发生突变,GA中的变异算子就是让染色体现有的基因发生突变,以增加种群染色体基因的多样性。变异算子可以避免算法早熟收敛,提高遗传操作的全局寻优能力。

3.5 SA操作

SA操作的目的是拓展算法局部搜索的能力,主要分为生成邻域解和判断接纳新解两部分。

3.5.1 生成邻域解

对于遗传操作生成的新种群,随机选择交换、逆转或插入的方式生成邻域解。

交换操作:如图3所示,随机选择染色体的两个位置,交换两个位置上的元素,对于一条长度为8的染色体“12345678”,随机选择了位置2和位置7,交换后的染色体变为了“17345628”。

图3 交换操作示意图Fig.3 Schematic diagram of exchange operation

逆转操作:如图4所示,随机选择染色体的两个位置,对两个位置之间的元素进行逆序排列,对于一条长度为8的染色体“12345678”,随机选择了位置2和位置7,逆转后的染色体变为“17654328”。

图4 逆转操作示意图Fig.4 Schematic diagram of reverse operation

插入操作:如图5所示,随机选择染色体的两个位置,抽取第1个位置上的元素插入到第2个元素后面,对于一条长度为8的染色体“12345678”,随机选择了位置2和位置7,逆转后的染色体变为“13456728”。

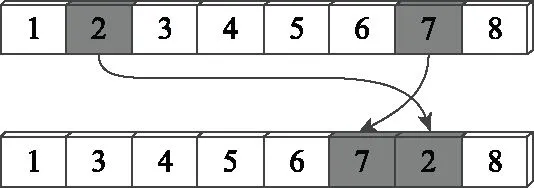
图5 插入操作示意图Fig.5 Schematic diagram of insert operation

3.5.2 判断接纳新解

引用Metropolis准则对生成的邻域解进行甄别,保留其中潜在的优秀个体。其中,Metropolis准则可表示为

(14)

式中:xbefore代表子种群中的旧解;xafter代表邻域解;T0为初始温度;k为冷却因子。若邻域中的新解的适应度值高于旧解,则无条件保留新解,否则根据两者的适应度值差值概率公式p=exp(-Δf/(kT0))来判断是否选择该个体。

3.6 算法终止条件

本文通过预设进化代数来控制算法的终止,这样可以有效求解算法的精度和运行时间。算法运行过程中,每一次迭代进化后,都会判断其是否达到预设值。如果达到,算法停止,输出最优解;如果没有达到,则算法继续运行。

3.7 算法流程

HGA的基本流程如下。

步骤 1设定初始参数,主要包括种群数、迭代次数、遗传操作概率、初始温度、冷却因子等;

步骤 2初始化种群;

步骤 3计算种群个体适应度值;

步骤 4判断遗传运算终止条件,选择继续运算或输出最优解;

步骤 5对初始种群进行选择、交叉、变异3种遗传操作,得到子种群;

步骤 6通过随机概率选择不同方法,生成随机邻域解,即新解;

步骤 7计算新解适应度值并与旧解比较,若新解适应度更高,直接用新解替换旧解,如果新解适应度低,则按照exp(-Δf/(kT0))是否大于随机值random(0,1)的方式保留新解,Δf为新解与旧解的差值;

步骤 8判断SA运算终止条件,选择重复步骤6和步骤7或执行步骤3。

具体的算法流程如图6所示。

图6 HGA流程图Fig.6 Flowchart of HGA

4 算例分析

为验证模型可行性,对比算法的改进效果,分别使用经典GA和HGA对战机数为30、50、100的物资配送任务进行模拟运算。战机物资配送需求表如表1所示,包含物资配送中心和战机点位坐标、物资需求、物资接收时间窗以及物资卸载时间等信息。

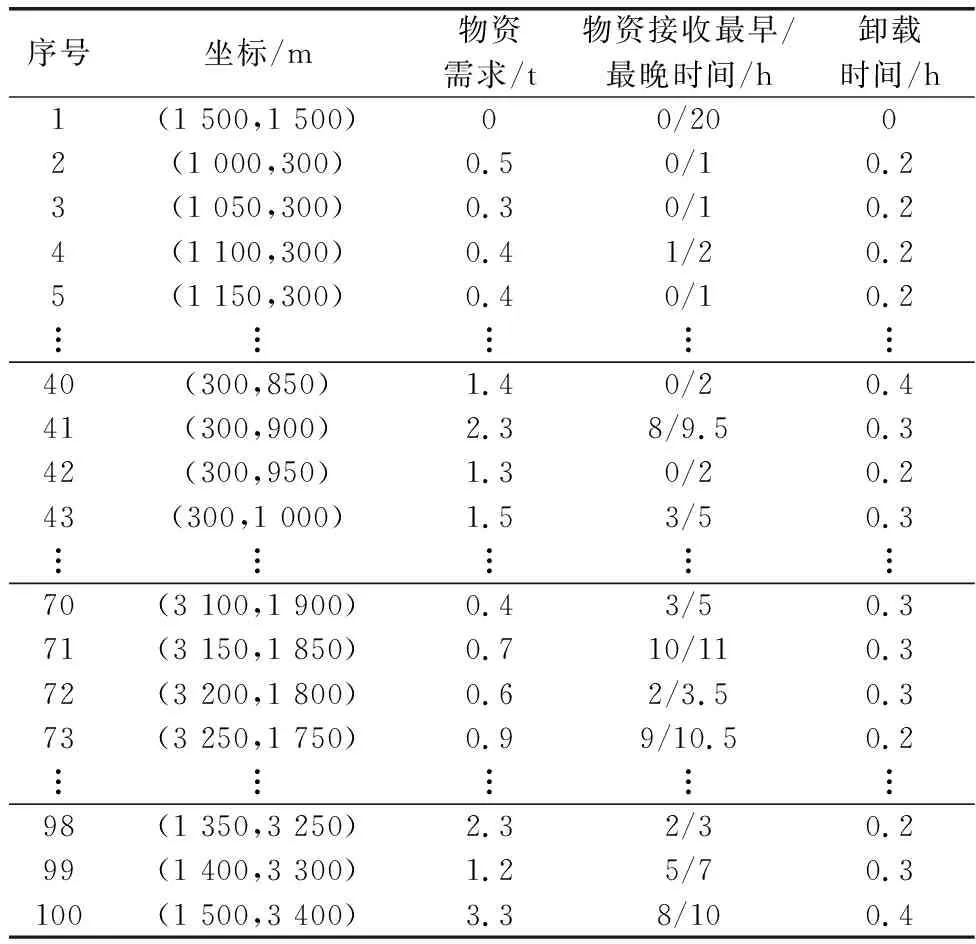
表1 战机物资配送需求

使用装有Inter(R)Core(TM)i-79750H 8核2.6 GHz CPU的电脑对模型进行计算。设定初始种群个数为200,遗传迭代次数为500,交叉概率为0.9,变异概率为0.05,代沟为0.9,SA操作迭代次数为200,初始温度为100,冷却因子为0.99,交换操作概率为0.2,逆转操作概率为0.5,插入操作概率为0.3。可调度最大车辆数为25,单个车辆最大装载重量为20 t,车辆行驶速度为5 000 m/h。为使结果更加客观公正,每种算法各运行20次,求其平均值进行对比,运算结果如表2所示,HGA求解出的方案路线如图7～图9所示,计算100架战机任务的优化过程如图10所示。

表2 运算结果

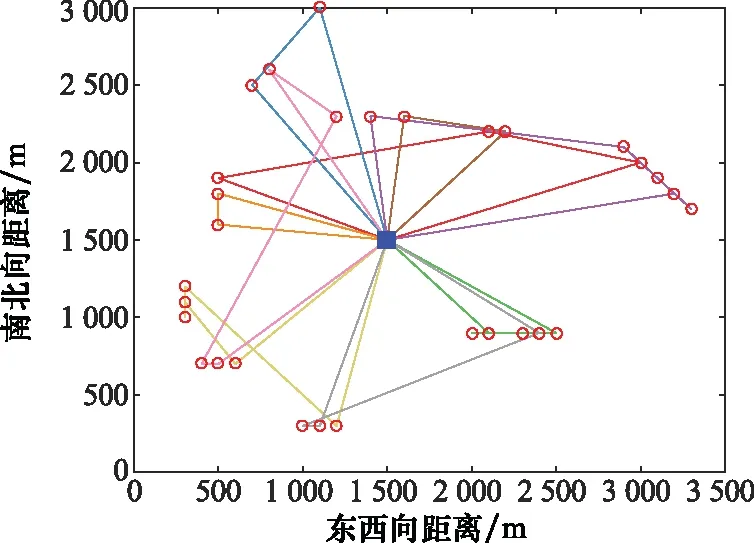
图7 30架战机物资配送方案路线图Fig.7 Route map for materiel distribution of 30 fighters

图8 50架战机物资配送方案路线图Fig.8 Route map for materiel distribution of 50 fighters

图9 100架战机物资配送方案路线图Fig.9 Route map for materiel distribution of 100 fighters

图10 优化过程示意图Fig.10 Schematic diagram of optimization process

分析运算结果不难发现,HGA的运算时间基本保持在200～330 s,是经典GA的4～5倍,但在可接收的范围之内。对比车辆数目和车辆总行驶距离,HGA均优于经典GA,而且随着战机数量的增加,优化的效果更加明显。图10中,蓝色曲线代表经典GA的优化过程,红色曲线代表HGA的优化过程。迭代50次之前,两种运算结果差别不大,经典GA在极少时间优于HGA;迭代50次之后,HGA全时间段优于GA。从曲线的变化趋势来看,蓝色曲线有多个位置变成水平直线,这就意味着运算陷入了局部最优,红色曲线基本没有变成水平直线的情况,但有少部分逆增长的位置,这就是SA操作起到了作用,突破了算法陷入局部最优的僵局。整体而言,改进后的HGA比经典GA的表现更加优秀。

5 结束语

本文以提高海军航空兵场站物资配送效率、减少工作成本为目标,在时间窗和车辆载重的约束下构建了数学模型,提出了引入SA操作的HGA。对比实验表明,所提算法优于经典GA,达到了配送车辆调度智能优化的需要。本文建立的调度模型受限于任务已知、且无外界突发状况干扰的情况,但在现实保障工作中,飞行计划还会受到天气、战机状态、航空管制等多种因素的影响,飞行保障需求也会随之变更,后续可针对动态保障需求进行进一步研究。