轻夸克物质团、奇异子和致密矮星∗

刘珈亦 范子萱 王立经 夏铖君 徐仁新

(1 扬州大学物理科学与技术学院引力与宇宙学研究中心 扬州 225009)

(2 北京大学物理学院天文学系 北京 100871)

(3 北京大学核物理与核技术国家重点实验室 北京 100871)

1 引言

量子色动力学(Quantum Chromodynamics)表明强相互作用同时具有渐近自由和色禁闭两个基本性质, 因此人们预期核物质在密度足够大后会发生解禁闭相变生成夸克物质. 该过程及其逆过程在地面实验室中难以实现, 但是却有可能在极端天体环境下不断发生, 如恒星演化末期的引力塌缩过程、双星系统的并合过程甚至宇宙演化的早期.

对于夸克物质的性质, 最早人们猜想由u、d、s夸克构成的奇异夸克物质比核物质更稳定[1–3], 因此宇宙中可能存在各类由奇异夸克物质构成的物体, 如奇异子[4–7]、奇异核素[8–9]、超密陨石[10]以及奇异星[11–13]等. 然而, 近期一些研究表明, 手征对称性自发破缺将会导致s夸克质量太大, 使奇异夸克物质不再稳定[14–15]. 在这种情况下, 奇异夸克物质只可能存在于混杂星的中心或在重离子碰撞实验过程中短暂地产生并迅速衰变.

另一方面, 在线性σ模型框架内, 通过拟合强子谱的实验数据, 人们发现仅由u、d夸克构成的轻夸克物质(ud夸克物质)可能更稳定[16], 此后其他模型也得到了相同的结论[17–21]. 因此, 与奇异夸克物质类似, 宇宙中可能存在ud夸克物质团[16,18]和ud夸克星[17,19–21]. 进一步研究发现, 若ud夸克物质的对称能较大, 那么其物质团会在特定大小时最稳定[22–23]. 此时更重的ud夸克物质团会发生裂变, ud夸克星表面则会碎裂成由这类物质团和电子构成的壳层结构. 而除此之外, 甚至存在完全由ud夸克物质团和电子构成的致密矮星, 即ud夸克矮星[22–23].

本文主要探讨ud夸克物质对称能及其对ud夸克物质团性质的影响, 并在此基础之上进一步讨论ud夸克矮星的结构和性质. 我们发现, 在对称能较大时重子数A ≈1000附近的ud夸克物质团最稳定.而相较于传统的白矮星, ud夸克矮星通常具有较小的半径, 被正常物质覆盖的ud夸克矮星的半径则在它们之间, 这与最近观测到的质量和半径都异常小的白矮星相符.

2 原子核、ud夸克物质团以及奇异子

为了得到原子核、ud夸克物质团以及奇异子的性质, 我们首先对构成这些物质集团的核物质(Nuclear Matter, NM)、ud夸克物质(ud Quark Matter, udQM)和奇异夸克物质(Strange Quark Matter, SQM)在不考虑有限体积效应下的单位重子能εDM做二阶展开, 即

这里的二阶展开系数εs表示对称能, 自变量fZ≡Z/A为比电荷, 其中Z和A分别表示电荷数和重子数. 当fZ=fZ0时单位重子能最小(εDM=ε0),其对应的比电荷fZ0及最小单位重子能ε0在表1中列出. 需要指出的是, 原子核、ud夸克物质团以及奇异子的密度随重子数A的变化较小. 因此, 为了方便计算, 我们忽略了重子数密度变化的影响, 并假定(1)式对应物质的重子数密度为n0.

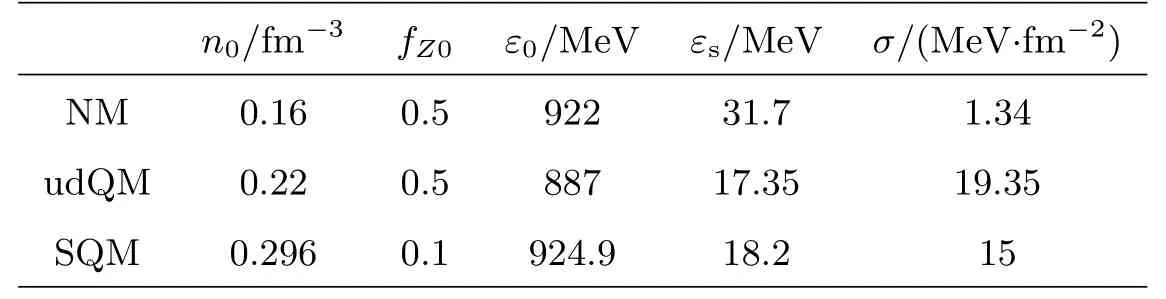
表1 本文采用的对应于核物质(NM)[24–25]、ud夸克物质(udQM)[16]和奇异夸克物质(SQM)[26]的参数组. 除此之外, 对于ud夸克物质和奇异夸克物质, 我们还考虑了更大的对称能(εs = 32、40、60 MeV)Table 1 The adopted parameter sets for nuclear matter (NM)[24–25], ud quark matter (udQM)[16], and strange quark matter (SQM)[26]. Larger symmetry energies are adopted for udQM and SQM as well(i.e., εs = 32, 40, 60 MeV)

表1列出了(1)式中由各类模型得到的核物质[24–25]、ud夸克物质[16]和奇异夸克物质[26]的参数组. 值得一提的是, 表1中奇异夸克物质单位重子能最小处的比电荷fZ0= 0.1是由微扰模型取特定参数组情况下得到的[26]. 而实际上采用其他参数组或模型时fZ0的具体取值会稍有不同, 甚至对于色味锁定的奇异夸克物质fZ0= 0. 除此之外,对于ud夸克物质和奇异夸克物质, 表1所列的对称能εs主要来源于夸克动能的贡献, 而夸克之间的相互作用(如形成u-d夸克库伯对)将会大大改变εs的具体取值[27–31]. 因此我们进一步考虑了εs= 32、40、60 MeV的情形来探讨夸克物质对称能对ud夸克物质团、奇异子以及ud夸克矮星的影响.

在液滴模型框架内, 考虑有限体积效应, 重子数A和比电荷fZ给定的原子核、ud夸克物质团以及奇异子的单位重子能(εNugget)由下式得到

这里的第一项由(1)式给出,第二项对应于库伦相互作用的贡献(精细结构常数α= 1/137), 而第三项则来源于表面能. 表面能的具体取值由表面张力σ和物质集团的表面积决定. 对于不同的物质类型,σ的取值也存在较大差异, 表1列出了σ的典型值. 对于给定的重子数A, 我们对(2)式进行变分, 得到物质集团满足β平衡条件时的比电荷, 即

对于给定重子数A和比电荷fZ的物质集团, 其所带的电荷为Z=fZA.

图1给出了液滴模型预言的原子核、ud夸克物质团以及奇异子的比电荷和单位重子能随重子数A的变化关系, 其中比电荷满足β平衡条件, 由(3)式确定. 由图中黑色实线可知, 随着重子数A增加,β稳定线上原子核的比电荷fZ从0.5附近开始单调下降, 而单位重子能却存在一个最小值εNugget=930 MeV, 对应于56Fe. 随着A增大,εNugget开始不断增加, 此时原子核容易发生裂变并变得越来越不稳定, 最终能够被实验证认的β稳定原子核在266Hs终结, 而目前实验室合成的最重原子核则为294Og[35].原子核单位重子能存在极小值(56Fe)表明恒星核合成存在终点1取决于恒星的质量, 核合成可能在56Fe之前就结束., 是白矮星产生和存在的必要条件.

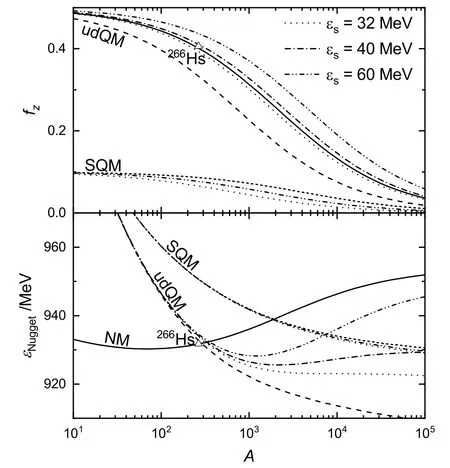
图1 满足β平衡条件的原子核、ud夸克物质团以及奇异子的比电荷(fZ, 上)和单位重子能(εNugget, 下). 图中三角形代表当前实验测得的最重β稳定原子核266Hs[32–34], 若ud夸克物质团的单位重子能小于266Hs则可以被排除.Fig.1 Charge-to-mass ratio (fZ, upper panel) and energy per baryon (εNugget, lower panel) for β-stable nuclei, udQM nuggets, and strangelets. The experimental data for the heaviest β-stable nucleus 266Hs is indicated with the open triangle[32–34], which rules out the udQM nuggets that are more stable than 266Hs.

对于ud夸克物质团和奇异子,fZ和εNugget都随重子数A单调下降, 并且当A足够大时εNugget<930 MeV. 这表明ud夸克物质和奇异夸克物质都有可能比核物质更稳定,在A ≈1057时就会形成ud夸克星或奇异星. 除此之外, 我们发现ud夸克物质团的比电荷与原子核类似, 这主要是因为它们都由两味夸克构成, 在fZ= 0.5时, ud夸克物质和核物质能量最低. 而奇异子的比电荷比ud夸克物质团小得多, 其主要原因是奇异夸克物质由数量大致相同的u、d、s夸克构成. 另一方面, 由于目前实验上还没有发现有原子核衰变成为ud夸克物质团, 因此可以采用最重的β稳定原子核266Hs的单位重子能作为ud夸克物质团的下限. 由图1可知, 本文选取的参数组所对应的ud夸克物质团都满足这一要求. 在此基础之上, 我们进一步增大对称能使其达到εs=32、40、60 MeV, 以探讨对称能对ud夸克物质团和奇异子性质的影响. 我们发现, 随着εs增加, ud夸克物质团和奇异子的比电荷都增加并且趋近fZ0,其对应的每重子能量也增大并趋近于(2)式给出的εNugget(A,fZ0). 由于奇异子的比电荷较小并接近fZ0, 其能量增大的幅度不明显. 而对称能对ud夸克物质团的影响则大得多,由于额外增加的库伦排斥,其单位重子能εNugget在A较大(≿103)时随着εs显著增加, 并在A较小(≾102)时εNugget保持不变. 此时就会出现ud夸克物质团在特定大小(A ≈1000)时最稳定的情形. 在这种情况下, 类似于原子核单位重子能存在极小值的情形, 更重的ud夸克物质团将会发生裂变, 并且还可能存在由这类ud夸克物质团和电子组成的晶体结构, 形成ud夸克星的外壳和ud夸克矮星.

3 白矮星和致密矮星

为了计算得到ud夸克物质团或原子核与电子构成的晶体结构, 我们这里采用BPS (Baym-Pethick-Sutherland)模型[36], 即假定物质集团为球形, 沉浸在均匀分布的电子气当中并构成体心立方晶体. 在给定平均重子数密度nb、物质集团比电荷fZ以及重子数A的情况下, 具有体心立方晶格结构的致密物质的能量密度为

这里的第一项由液滴模型(2)式给出, 代表物质集团的能量密度. 其对应的物质集团数密度为nd=nb/A、Wigner-Seitz (WS)原胞半径为RW= (3A/4πnb)1/3、物质集团的半径为Rd= (3A/4πn0)1/3. 第二项对应于体心立方晶格的能量贡献[37]. 第三项则是电子的能量密度, 由下式可得

其中电子质量me=0.511 MeV,

在给定平均重子数密度nb的前提下, 我们对(4)式关于fZ和A作变分, 得到能量密度的极小值,即对应于β稳定的冷白矮星或ud夸克矮星物质的能量密度. 图2分别展示了由原子核和ud夸克物质团构成的白矮星和ud夸克矮星物质的微观结构. 由左图可知, 白矮星和ud夸克矮星内部物质集团的半径Rd远小于WS原胞半径RW, 即星体内部大部分空间被电子填充. 在较低密度时, 白矮星和ud夸克矮星物质所对应的Rd、A、Z主要对应于图1中单位重子能最低点. 随着nb增加,Rd逐渐增大, 与之对应的A和Z也增大, 而RW则不断减小. 这就造成了各类物质集团的空间占比随nb增加不断增大. 对于由核物质构成的传统白矮星, 当原子核间距足够近时就会发生中子滴出, 此时白矮星就不再稳定,因此这类物质只能在中子星内壳层中稳定存在[38].对于由ud夸克物质团构成的ud夸克矮星, 当其密度足够高时就会发生一阶相变转变成均匀ud夸克物质, 形成ud夸克星[23]. 对比传统的白矮星物质和ud夸克矮星物质, 我们发现ud夸克物质团比原子核大得多, 其对应的WS原胞、A以及Z也更大. 此外, 由于BPS模型采用了真实的包含壳效应的原子核质量, 因此白矮星物质中原子核的A和Z随密度会发生突变. 而这里我们采用液滴模型来得到原子核的结构和性质, 因此A和Z随密度均匀变化, 反映了白矮星物质中原子核的平均性质. 尽管如此, 两种方法得到的能量密度基本相同.

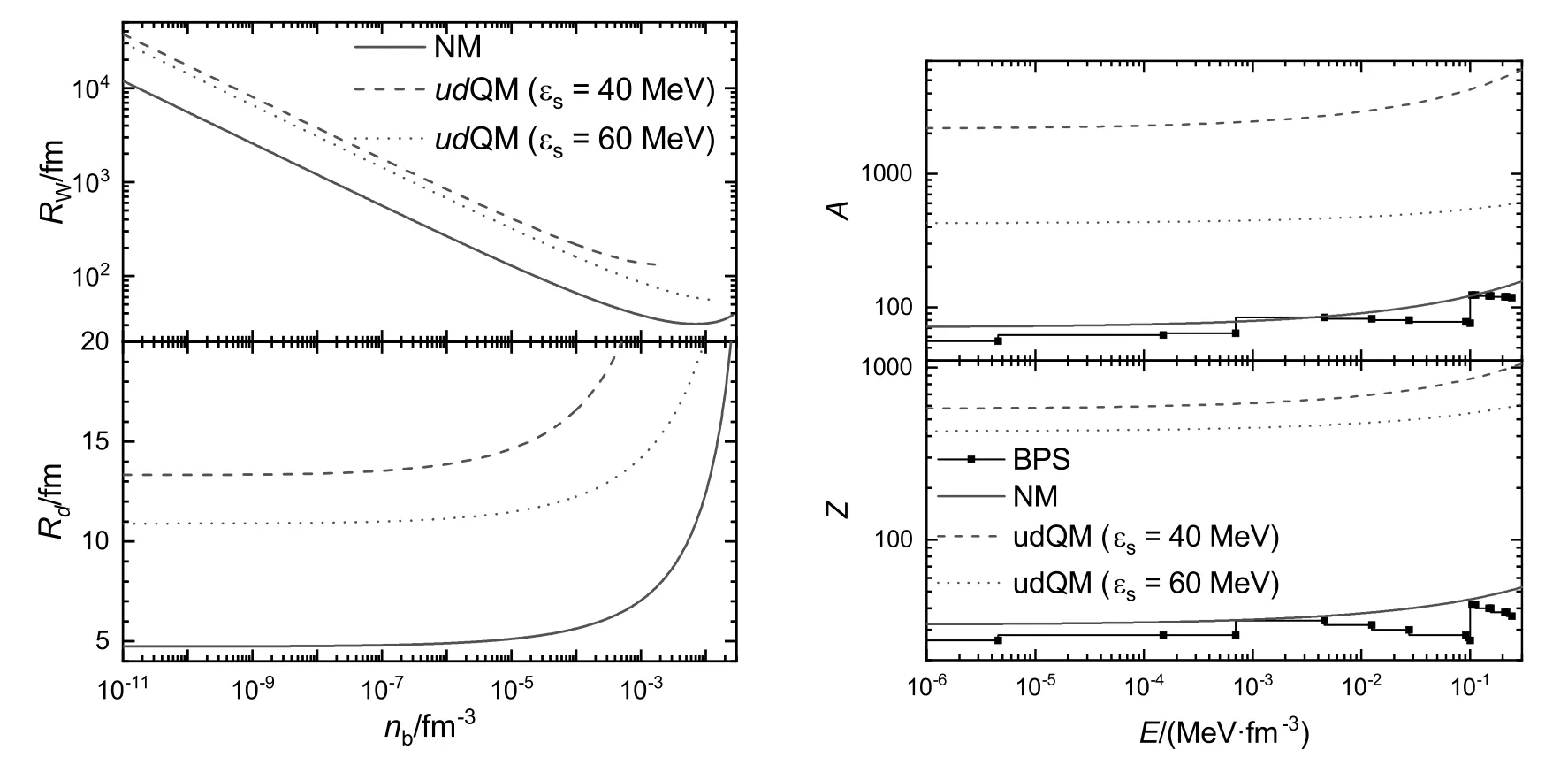
图2 白矮星和ud夸克矮星内部液滴相所对应的半径Rd、WS原胞半径RW、重子数A以及电荷数Z. 而Baym等(BPS)的计算得到的结果也已在右图中标明[36].Fig.2 Droplet size Rd, WS cell radius RW, baryon number A, and charge number Z for the droplet phase in white dwarfs and udQM dwarfs. The corresponding values fixed by Baym et al.[36](BPS) are indicated as well.

基于(4)式预言的白矮星和ud夸克矮星物质的能量密度, 可进一步计算得到其对应的压强, 即

由此我们就得到了白矮星和ud夸克矮星物质的状态方程. 在此基础之上, 通过求解Tolman-Oppenheimer-Volkoff方程

就可以得到与之对应的白矮星和ud夸克矮星的质量-半径关系. 其中(7)式中G=6.707×10-45MeV-2为引力常数,r为球对称星体内部径向坐标,m(r)表示通过坐标r的同心球体所包围的星体物质总质量,由(8)式积分得到. 图3展示了我们计算得到的白矮星和ud夸克矮星物质的状态方程及由此得到的质量-半径关系. 整体上来说, 在相同的压强下, ud夸克矮星物质的能量密度要比传统白矮星物质高得多.因此,ud夸克矮星会比传统白矮星更致密,其质量和半径都要小得多. 此外, 随着对称能增加, ud夸克矮星物质的压强变大, 其对应的ud夸克矮星的半径也增大. 图3左图中黑色实线给出了本文得到的传统白矮星状态方程, 与BPS状态方程基本相同[36]. 相较于图3右图中展示的质量大于0.5M⊙的4颗典型白矮星的质量和半径[39], 我们得到的白矮星质量和半径都稍小. 若进一步考虑温度、磁场以及不同的原子核组分, 白矮星的质量和半径将增大并与观测相符. 然而, 图中7颗质量和半径都异常小的白矮星[40]却无法用传统白矮星模型来解释, 传统模型得到的半径都远大于观测值. 另一方面, 尽管ud夸克矮星比传统白矮星更致密, 但是其半径却比观测值小得多.

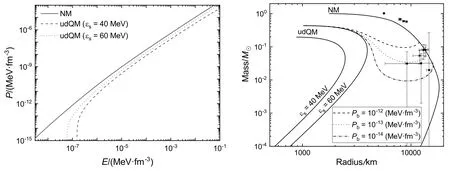
图3 左图: 白矮星和ud夸克矮星物质所对应的状态方程. 右图: 白矮星和ud夸克矮星的质量-半径关系, 其中三条虚线对应于ud夸克矮星表面覆盖正常物质的情形. 图中质量大于0.5 M⊙的4个点代表典型白矮星的质量和半径[39], 而下面的7个点表示质量和半径都异常小的白矮星[40].Fig.3 Left: Equation of states for dense stellar matter in white dwarfs and udQM dwarfs. Right: Mass-radius relations of white dwarfs and udQM dwarfs, where the three dashed curves indicate udQM dwarfs covered by normal matter. The four dots with masses larger than 0.5 M⊙indicate the typical white dwarfs’ masses and radii[39], while the seven dots below present the white dwarfs with unusually small masses and radii[40].

为了解释这7颗白矮星, 文献[40]假定其中心存在奇异夸克物质内核, 内核表面有极强的电场以支撑由正常物质构成的壳层结构. 在这里我们则考虑ud夸克矮星覆盖正常物质的情形, 假设两类物质分界面处的压强分别为Pb= 10-12、10-13、10-14MeV·fm-3, 那么相应的状态方程可由图3左图的两类状态方程组合得到, 即P>Pb处取ud夸克矮星物质状态方程, 而P≤Pb处采用正常物质状态方程. 由此得到的质量-半径关系如图3右图的虚线所示, 能够将ud夸克矮星(εs= 60 MeV)和传统白矮星连接起来. 与奇异夸克物质的情形不同,由图2可知, 在被正常物质覆盖的ud夸克矮星内部,分界面上原子核和ud夸克物质团的重子数A存在较大差别, 因此要将正常物质转变成ud夸克物质需要由多个原子核熔合得到, 相关的反应过程需要同时克服图1处的能量位垒和核熔合的库伦位垒, 因此难以进行. 另一种可能性是通过不断熔合原子核和ud夸克物质团, 形成较大的ud夸克物质团并由此裂变得到稳定的ud夸克物质团, 而该反应同样需要克服极高的库伦位垒[26]. 因此, 可以认为在冷白矮星中正常物质转变成ud夸克物质效率极低, 两种物质可以同时存在. 除此之外, 当白矮星内部出现ud夸克物质团之后质量降低, 即∂m/∂nc<0 (其中nc为该致密矮星中心密度). 由于此时致密矮星由两种不容易互相转化的物质构成, 我们认为致密矮星可能仍然稳定[41–43]. 在这种情况下, 被正常物质覆盖的ud夸克矮星就能够解释最近观测到的质量和半径都异常小的白矮星[40].

4 总结与展望

本文研究了由核物质、奇异夸克物质和ud夸克物质构成的物质集团, 即原子核、奇异子以及ud夸克物质团的性质及稳定性. 随着对称能增加,ud夸克物质团和奇异子的比电荷都增加, 其对应的单位重子能也增大. 尽管如此, 奇异子能量增大的幅度不明显, 而ud夸克物质团在重子数A较大(≿103)时随对称能显著增加. 此时就会出现ud夸克物质团在特定大小(A ≈1000)时最稳定的情形, 并能够形成由ud夸克物质团和电子构成的致密矮星,即ud夸克矮星. 在此基础之上, 我们进一步讨论了传统白矮星和ud夸克矮星的结构和性质. 我们发现, 相较于传统的白矮星, ud夸克矮星通常具有较小的半径, 而其半径和质量也会随着对称能增加而增大. 若ud夸克矮星被正常物质覆盖, 则其对应的半径会在裸的ud夸克矮星和传统的白矮星之间, 这与最近观测到的质量和半径都异常小的白矮星相符[40]. 在本文的基础之上, 下一步我们将更细致地研究被正常物质覆盖的ud夸克矮星的稳定性及其演化过程, 讨论各类不同的脉动模式及可能的引力波辐射过程. 而对于奇异星或ud夸克星, 还有可能通过一些特殊的高能爆发现象如快速射电暴来寻找其存在的线索[44].