地月DRO星载光学测量近地小行星轨道确定∗

刘佳 宋叶志 黄乘利 胡小工 谭龙玉

(1 中国科学院上海天文台 上海 200030)

(2 上海科技大学物质科学与技术学院 上海 201210)

(3 中国科学院大学天文与空间科学学院 北京 100049)

(4 上海航天控制技术研究所 上海 201109)

1 引言

小行星的监测研究主要有两方面的意义, 一方面为未来小行星资源开发利用做准备[1–2], 另一方面可避免潜在危险小行星对地球构成碰撞威胁[3].历史上多次发生小行星撞击地球的事件: 6500万年前, 一颗直径约10 km的小行星撞击在墨西哥尤卡坦半岛, 是目前被认为造成恐龙在内的地球生物灭绝的重要原因[4]; 1908年俄罗斯通古斯地区发生小行星撞击事件, 波及范围达到2000 km2; 2013年一颗小行星撞击俄罗斯车里雅宾斯克地区后发生爆炸, 导致1200余人受伤[5]. 截至2022年7月19日, 全球已发现的近地小行星有29388颗, 其中潜在危险小行星2291颗. 为防范预警近地小行星对地球的撞击威胁,世界各国分别开展了对小行星的监测预警.

小行星监测预警分为多种方式, 根据观测位置分为地基观测和天基观测; 根据技术手段分为可见光观测、红外观测和雷达观测. 地基大口径望远镜是目前小行星监测预警的主力设备, 该设备建设成本低、作用距离远、方法成熟, 但对近太阳方向的监测存在盲区, 即使提高监测能力, 扩大覆盖范围,也很难提前发现和预警, 车里雅宾斯克爆炸就是因为地基望远镜未及时观测到小行星而造成严重损失. 2020年3月15日, 直径约26 m的小行星从向阳方向靠近地球, 距离地球仅有32.8万公里, 在最接近地球两天后才被发现; 随后在6月5日同样来自向阳方向的小行星2020 LD, 直径在89–200 m之间, 从距离地球306675 km处飞过, 在最接近地球两天后才被发现[6]. 与地基光学监测系统相比, 天基光学监测系统监测范围广、观测精度高, 满足对目标连续跟踪监视的需求, 可用来弥补地基观测设备的不足.

低地球轨道(Low Earth Orbit, LEO)、日地系统L1点轨道、类金星轨道、远距离逆行轨道(Distant Retrograde Orbit, DRO)以及地球领航轨道等位置是天基望远镜平台的主要部署轨道. Shao等[7]在2015年提出类金星轨道近地小行星搜索计划; 美国的民间组织提出哨兵任务, 计划将望远镜设在类金星轨道.美国的近地天体望远镜NEOCam(Near Earth Object Camera)计划预计2025年发射卫星到日地系统L1点轨道, 对地球附近的潜在危险小行星进行监测[8]. 2012年Valsecchi等[9]首次提出在DRO上放置一个由三颗卫星组成的星座,但没有进一步评估其探测能力. Stramacchia等[10]分析了位于日地系统DRO轨道上的监测星座的能力与特点.

与国外相比, 我国对小行星监测预警的研究起步较晚. 2016年, 国内提出了在类金星轨道部署卫星星座的NEA (Near-Earth Asteroid)普查与定位系统(Constellation of Heterogeneous Wide-field Near-Earth Object Surveyors, CROWN)方案[11];2022年, 李明涛团队和赵海斌团队提出了地球领航轨道近地小行星天基临近预警任务概念[6]; “嫦娥二号”月球探测器实现了我国对小行星的首次天基探测[12]; 国家航天局在2022年4月24日提出将着手组建近地小行星防御系统, 开始完善建立地基与天基对小行星的监测预警系统, 开展全球合作共同应对近地小行星撞击的威胁.

地月DRO属于逆行环绕月球的共振周期轨道,放置于此轨道上的飞行器能够长期保持稳定, 同时长期的轨道保持只需要较低的燃料成本.DRO距离地球及月球距离适中, 可与地球保持连续通信, 适用于深空探测、小行星预警与防护等长期隔离轨道任务. Bezrouk等人研究了稳定性长达30 yr且适合作为地月系统停泊轨道的DRO轨道族,距离月心的振幅小于50000 km和振幅在60000–80000 km的DRO轨道的稳定性非常好[13]. 即使DRO轨道相对于月球公转轨道面存在一定倾角, 稳定性也能达到数十年.

对于小行星而言, 精确的轨道根数能够有效准确预测出小行星的撞击概率. 因此为有效开展小行星监测预警工作, 首先要确定小行星的轨道. 本文基于地月DRO天基平台对近地小行星进行光学测量, 给出目标天体可视性条件和定轨原理, 通过仿真模拟光学测角数据对目标天体进行轨道确定, 将计算轨道与参考轨道比较,分析DRO平台对四种不同轨道类型的近地小行星的定轨性能.

2 地月DRO轨道

圆型限制性三体问题是研究地月空间轨道的常用模型, 地球m1和月球m2两个主天体看成质点,围绕公共质心做圆周运动, 第三体航天器受两个主天体引力影响, 但不影响两个主天体的运动. 采用质心旋转坐标系X-Y-Z描述圆型限制性三体问题,选取地月质心为坐标系原点,X轴由地心指向月心,Z轴取地月轨道方向. 引入质量参数表征圆型限制性三体问题, 地球和月球则分别位于-µm和1-µm处, 文献[14]给出了航天器在此系统中的动力学方程.

Hill限制性三体问题是一种特殊的圆型限制性三体问题, 适用于µm值小并且航天器轨道接近较小主天体的系统[10].µm= 0时, 可以将圆型限制性三体问题简化为旋转坐标系中的开普勒模型.H´enon[15]提出考虑µm趋近于0, 将方程组简化. 与圆型限制性三体问题中采用的质心旋转坐标系不同, Hill问题采用的会合坐标系ξ-η-ζ, 选取月球为坐标系原点, 地球在ξ轴负方向. 图1分别展示了圆型限制性三体问题和Hill问题采用的坐标系.

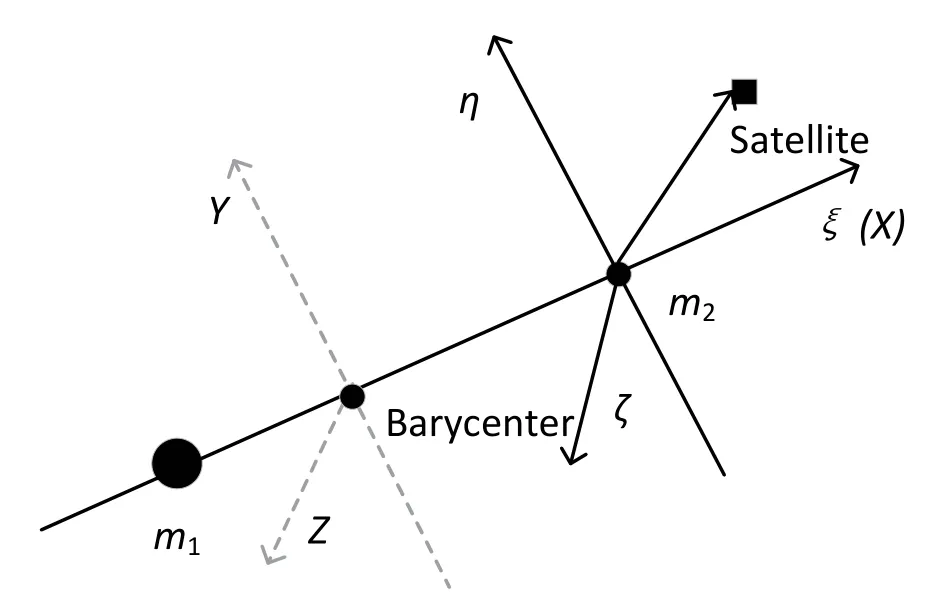
图1 圆型限制性三体问题和Hill限制性三体问题的坐标系Fig.1 Coordinate systems for planar circular restricted three-body problem and Hill’s problem

在Hill问题中, 第三体航天器的运动方程为:

H´enon等[15]对圆型限制性三体问题中的周期性轨道进行分类,分为f族、g族、a族、c族,DRO轨道族属于f族, 是圆型限制性三体问题中的一类特殊平面对称轨道族, 具有Lyapunov稳定性. 地月系统的DRO绕月逆行,对地球和月球有良好的覆盖性且轨道稳定, 适合深空中长期执行的任务. 文献[14]以圆型限制性三体问题为动力学模型研究了DRO轨道族周边的动力系统结构; 文献[16]研究了以地月为背景的DRO设计方法,分析了在实际力环境下地月DRO逆周期轨道的轨道特性和主要摄动因素.DRO轨道幅值范围较大, 当幅值较小时, DRO可以看作低轨的环月轨道, 此时月球为中心天体, 地球引力为摄动力; 而对于大幅值DRO, 地球影响显著,经典轨道根数不再适用, 文献[17]对其进行了相关研究. 本文中DRO轨道设计考虑了完整的力学模型, 运用数值方法进行计算. 在以月球中心为原点的旋转坐标系中, 用DRO的初始X振幅表示DRO的大小, 本文选取了DRO轨道族中初始X振幅为30000 km的一个稳定轨道上放置卫星监测近地小行星.

3 近地小行星的可视性分析

3.1 光学几何条件

天基平台卫星观测近地小行星时, 受到太阳光、极光、地球边缘辐射、其他天体的反射光和星光等光源干扰,其中太阳光是最主要的干扰因素.当平台卫星逆太阳光观测近地天体时, 会因背景光过于强烈无法观测目标. 定义目标–平台–太阳的夹角为θmin,仿真筛选数据的光学几何条件图如图2所示.

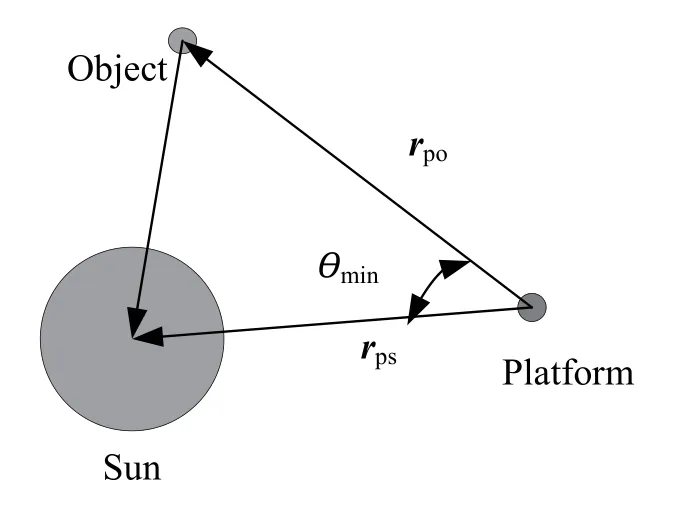
图2 光学几何条件Fig.2 Optical geometry constraints

本文仿真观测时, 设定满足可观测条件为θmin大于40◦时, 才能观测到目标天体, 即:

3.2 空间几何条件

观测平台观测目标天体时, 会受到地球、火星、月球等天体的遮挡, 导致平台无法观测到目标或观测精度较差. 以地球遮挡为例, 观测平台与目标天体的空间几何关系如图3所示.

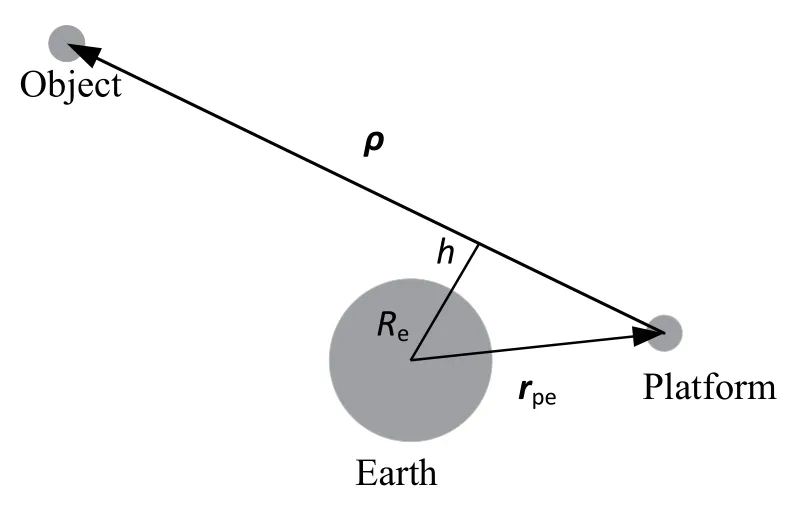
图3 空间几何条件Fig.3 Spatial geometry constraints

其中ρ为视线矢量,rpe为观测平台相对于地球的位置矢量,Re为地球半径,h为大气层高度.

此外目标天体观测时还会受到观测设备自身视场条件和可探测目标极限视星等等性能条件的约束. 本文小行星的可见性研究中只考虑了光学几何条件和空间几何条件的约束, 对于与相机设计有关的亮度可见性等条件约束暂时没有考虑.

4 天基光学定轨原理

近地天体围绕太阳运动的运动方程为:

其中µ=GMc为中心天体的引力常数,G为引力常数,Mc为中心天体的质量;Fε为摄动力, 近地天体的轨道大部分位于地球和火星之间, 考虑的摄动力主要是其他天体的引力摄动和后牛顿效应;r和˙r分别为位置和速度矢量;p为动力学参数;t0为初始历元,r0表示目标天体在t0时刻的位置矢量.

本文基于动力学定轨方法, 对近地小行星进行轨道改进. 在轨道改进中, 将目标天体的待求轨道参数称为状态量X,F(X,t)是和状态量相关的力学参数以及速度等,X0是待估状态量, 满足以下状态微分方程:

将卫星平台的光学测角数据(赤经、赤纬)记为观测量Y j, 其满足的观测方程为:

式中Y j是在tj时刻的一组观测量,j为某个时刻下标;G是相应观测量的理论值;Xj是目标天体在tj时刻的状态矢量;εj是在tj时刻的测量误差.

将观测方程和状态方程线性化, 得到精密定轨的基本方程[18]:

式中y为残差,是观测值与理论值之差;∆X是待估状态量的改正值;ε是测量误差;为状态转移矩阵,是目标当前状态向量对初始状态向量的偏导数,通常用Φ(t,t0)表示;X∗为某一时刻的参考状态量;为初始历元的参考状态量.

精密定轨的原理就是给出一组初始量, 利用大量观测数据, 求解方程(8), 得到待估状态量的改正值, 进而得到改进的状态量, 将改进的状态量作为估计量再次代入, 迭代计算, 得到满足精度的目标轨道解.

对于近地小行星所采用的定轨策略如表1所示, 其中QR中Q代表正交矩阵(Orthogonal matrix),R代表上三角矩阵(Upper triangular matrix);KSG为积分器发明人Krogh Shampine Gordon的缩写.

5 定轨仿真试验

本文选取四种不同轨道类型的小行星分别进行轨道确定, 表2为美国宇航局喷气推进实验室(Jet Propulsion Laboratory, JPL)提供的四颗小行星在日心黄道惯性系下的轨道根数, 其中a为轨道半长轴、e为轨道离心率、i为轨道倾角、Ω为升交点赤经、ω为近日点幅角、M为平近点角. 根据仿真条件测角精度2角秒, 数据采样间隔1 h, 观测近地小行星, 仿真生成观测数据. 此仿真条件考虑了第3节中介绍的光学几何条件和空间几何条件的约束. 在实际工程中可获取的测量数据还受到相机的工作模式和星上载荷的约束.

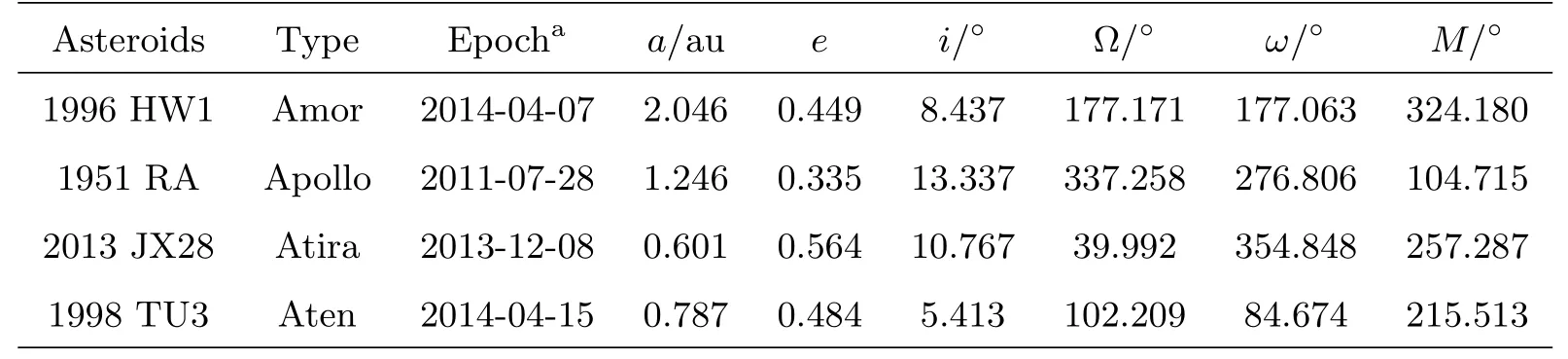
表2 近地小行星的轨道根数Table 2 Orbital roots of near-Earth asteroids

5.1 DRO平台观测小行星1996 HW1

小行星1996 HW1是1996年4月23日太空监测计划中的基特峰天文台所发现的一颗轨道类型为Amor型的近地小行星, 轨道周期为2.93 yr.

定轨弧段为2014年4月7日零时至2017年4月7日零时. 根据仿真条件, 仿真生成观测数据, 利用观测数据进行跟踪定轨, 定轨弧长3年的单平台观测残差如图4所示, 标题中POD为精密定轨(Precise Orbit Determination).

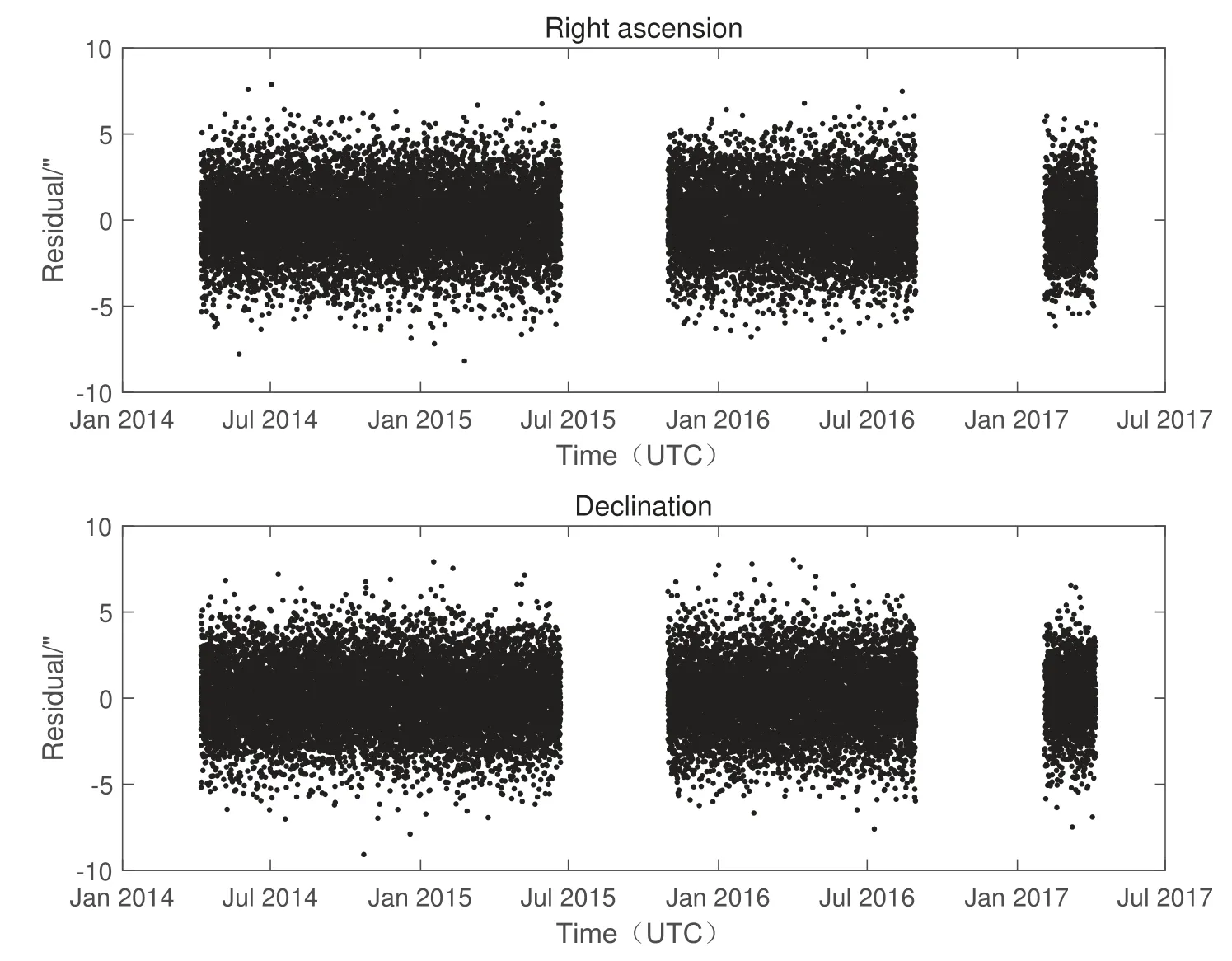
图4 单DRO对1996 HW1测量3年的POD残差Fig.4 3-year POD residuals of single DRO on 1996 HW1

图4上半部分为单DRO平台观测数据的赤经残差, 下半部分为观测数据的赤纬残差, 横坐标为观测时间(协调世界时, Universal Time Coordinated,UTC), 纵坐标为残差范围. 图5给出了单DRO对小行星1996 HW1跟踪定轨与仿真轨道在RTN坐标系下的比较结果, 其中R为径向、T为迹向、N为轨道面法向, RMS (Root mean square)为均方根偏差.图(a)为位置的偏差, 图(b)为速度的偏差, 横轴为观测时间, 纵轴为偏差范围, 轨道精度大致在30 km量级.图6给出了在相同仿真条件下,双DRO平台观测小行星1996 HW1的残差图, 图6中上图为平台1的观测残差, 下图为平台2的观测残差(后续残差图介绍同理).

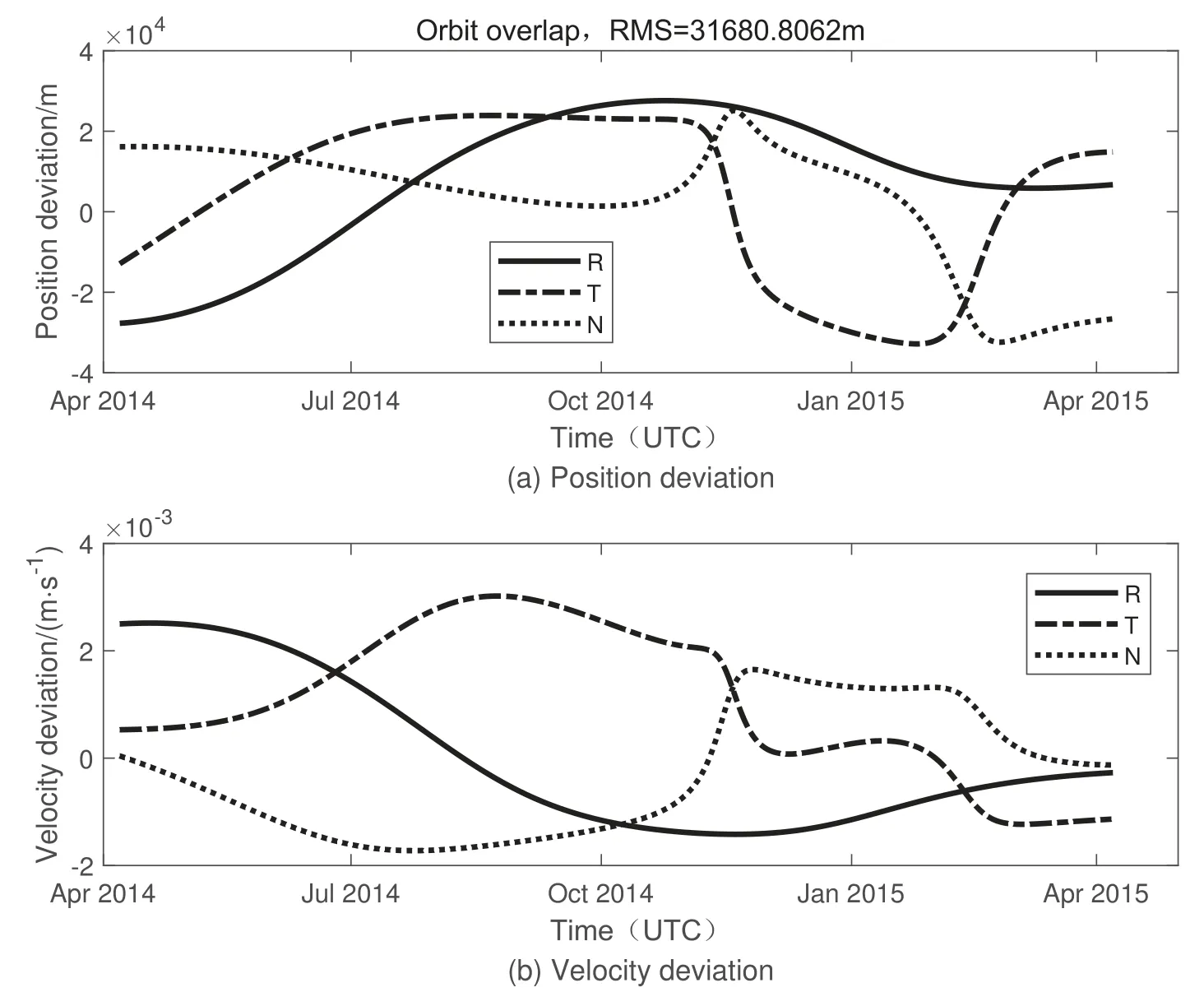
图5 单DRO对小行星1996 HW1定轨与仿真轨道比较Fig.5 Comparison between orbit determination and simulated orbit of single DRO on asteroid 1996 HW1

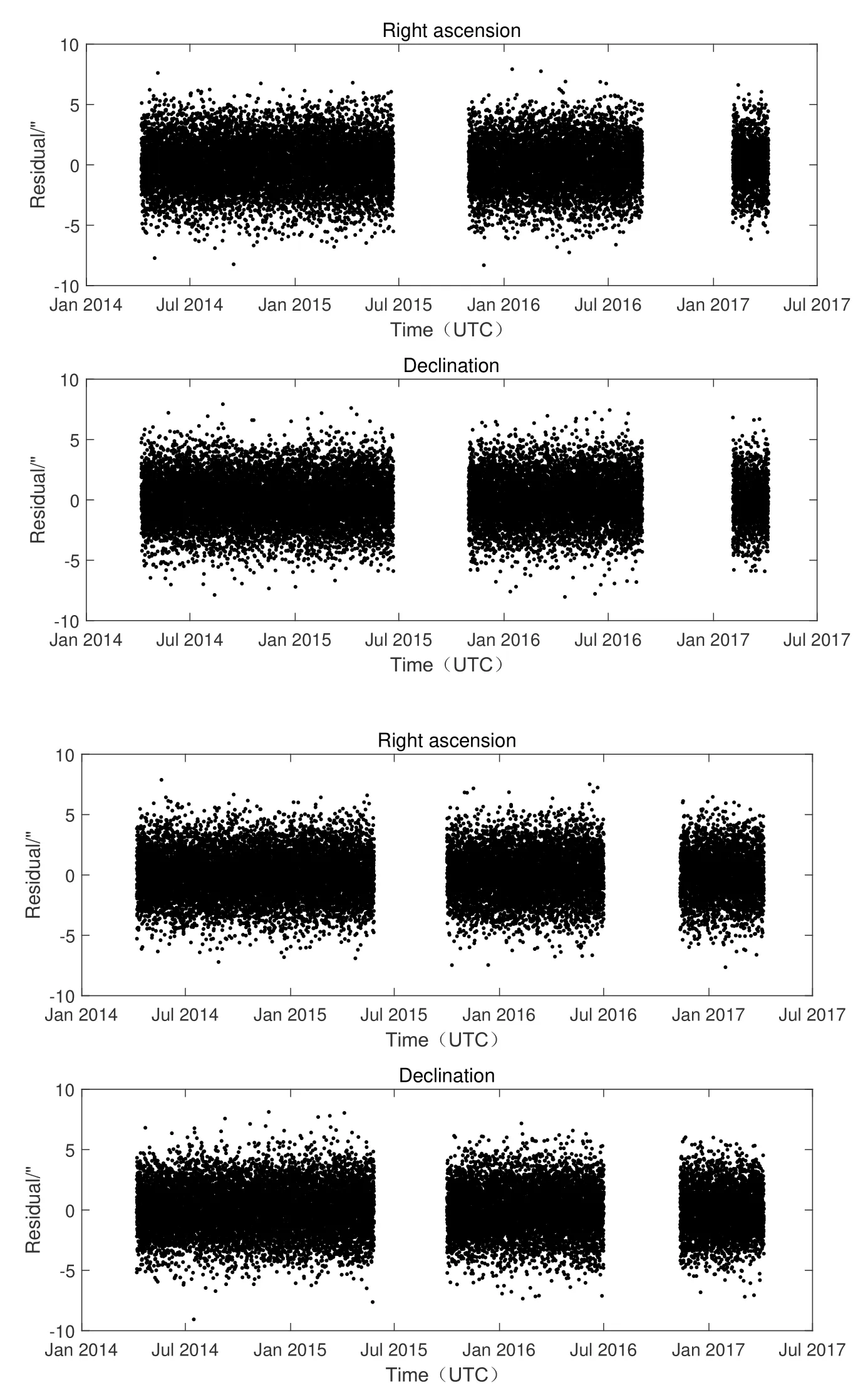
图6 双DRO对1996 HW1测量3年的POD残差Fig.6 3-year POD residuals of dual DRO on 1996 HW1

图7展示了在RTN坐标系下, 双DRO对1996 HW1跟踪定轨所得轨道与仿真轨道的比较结果,轨道精度大约在30 km左右.

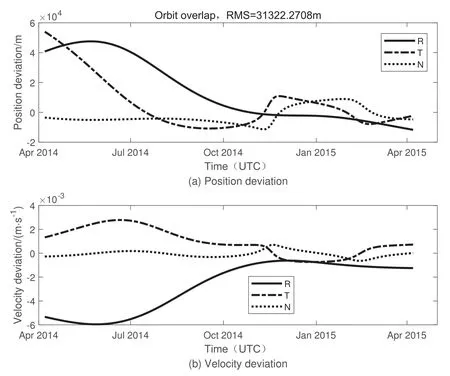
图7 双DRO对1996 HW1定轨与仿真轨道比较Fig.7 Comparison between orbit determination and simulated orbit of dual DRO on asteroid 1996 HW1

5.2 DRO平台观测小行星1951 RA

小行星1951 RA是1951年9月14日在帕洛玛发现的一颗轨道类型为Apollo型的潜在危险小行星,轨道周期为1.39 yr. 定轨弧段为2011年7月28日零时至2014年7月28日零时.

根据仿真条件, 仿真生成观测数据, 利用观测数据进行跟踪定轨, 定轨弧长3年单平台观测残差如图8所示.

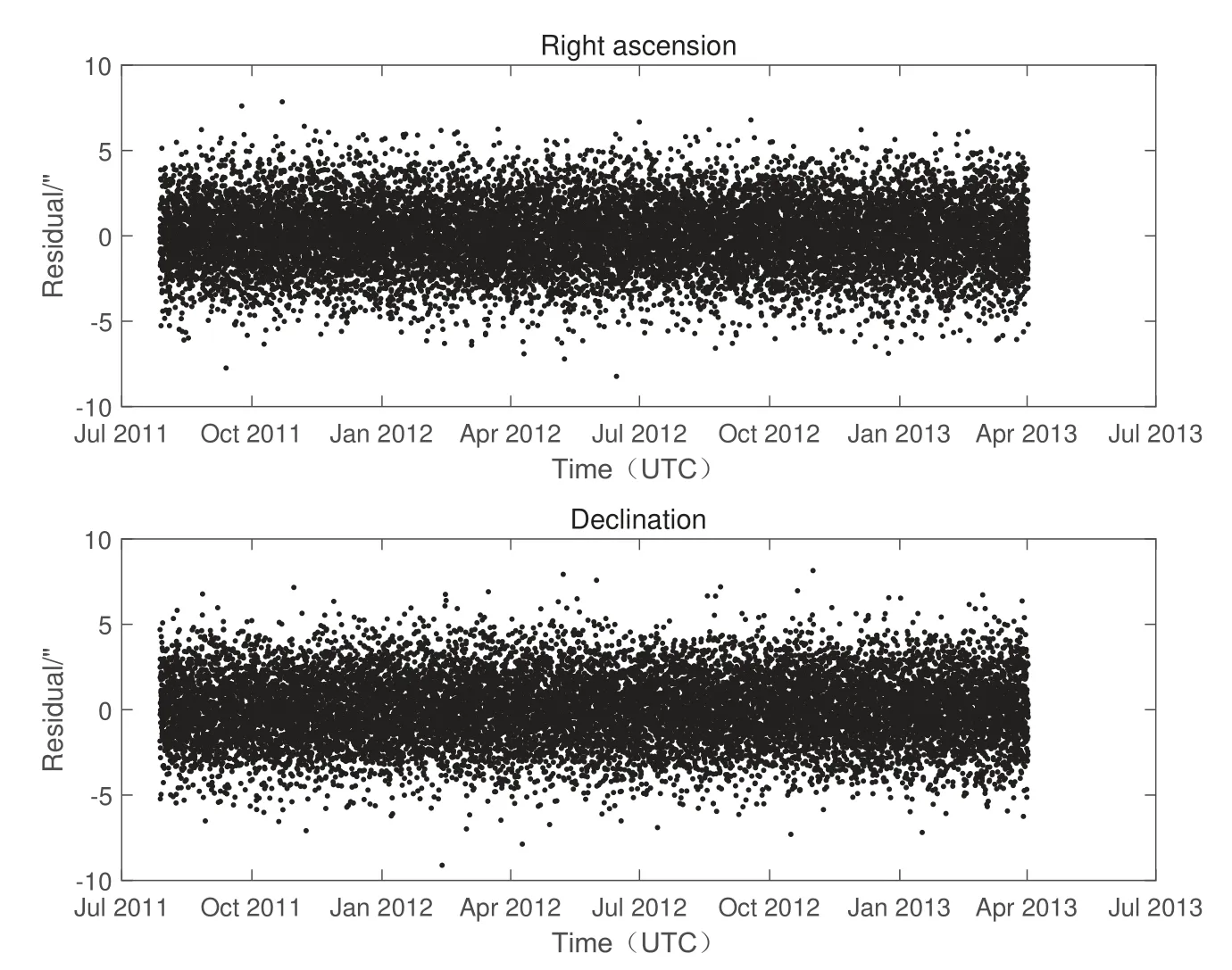
图8 单DRO对1951 RA测量3年的POD残差Fig.8 3-year POD residuals of single DRO on 1951 RA

图9给出了单DRO对小行星1951 RA跟踪定轨与仿真轨道在RTN坐标系下的比较结果, 定轨精度大约在100 km左右. 图10给出了在相同仿真条件下, 双DRO平台观测小行星1951 RA的残差图.

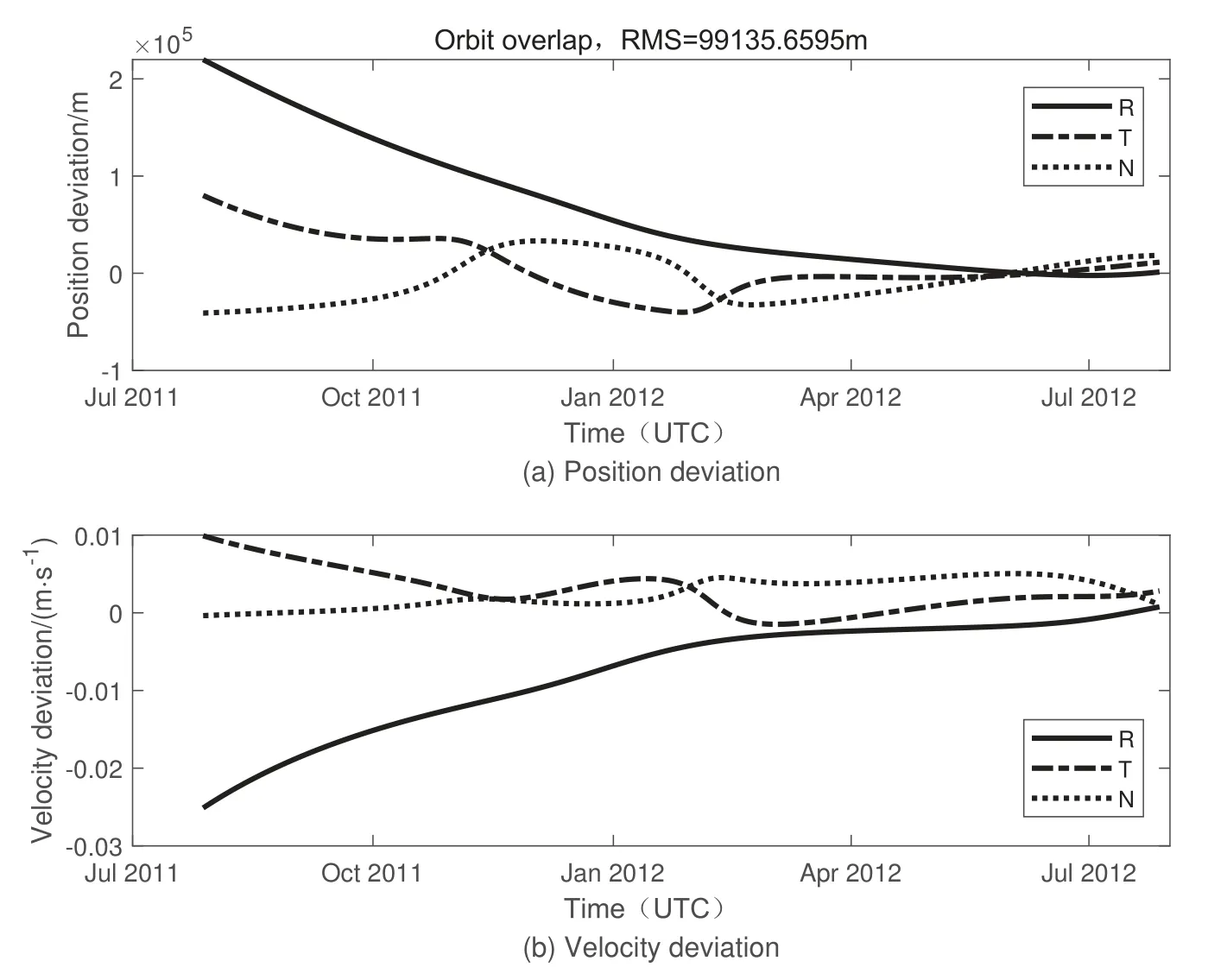
图9 单DRO对小行星1951 RA定轨与仿真轨道比较Fig.9 Comparison between orbit determination and simulated orbit of single DRO on asteroid 1951 RA

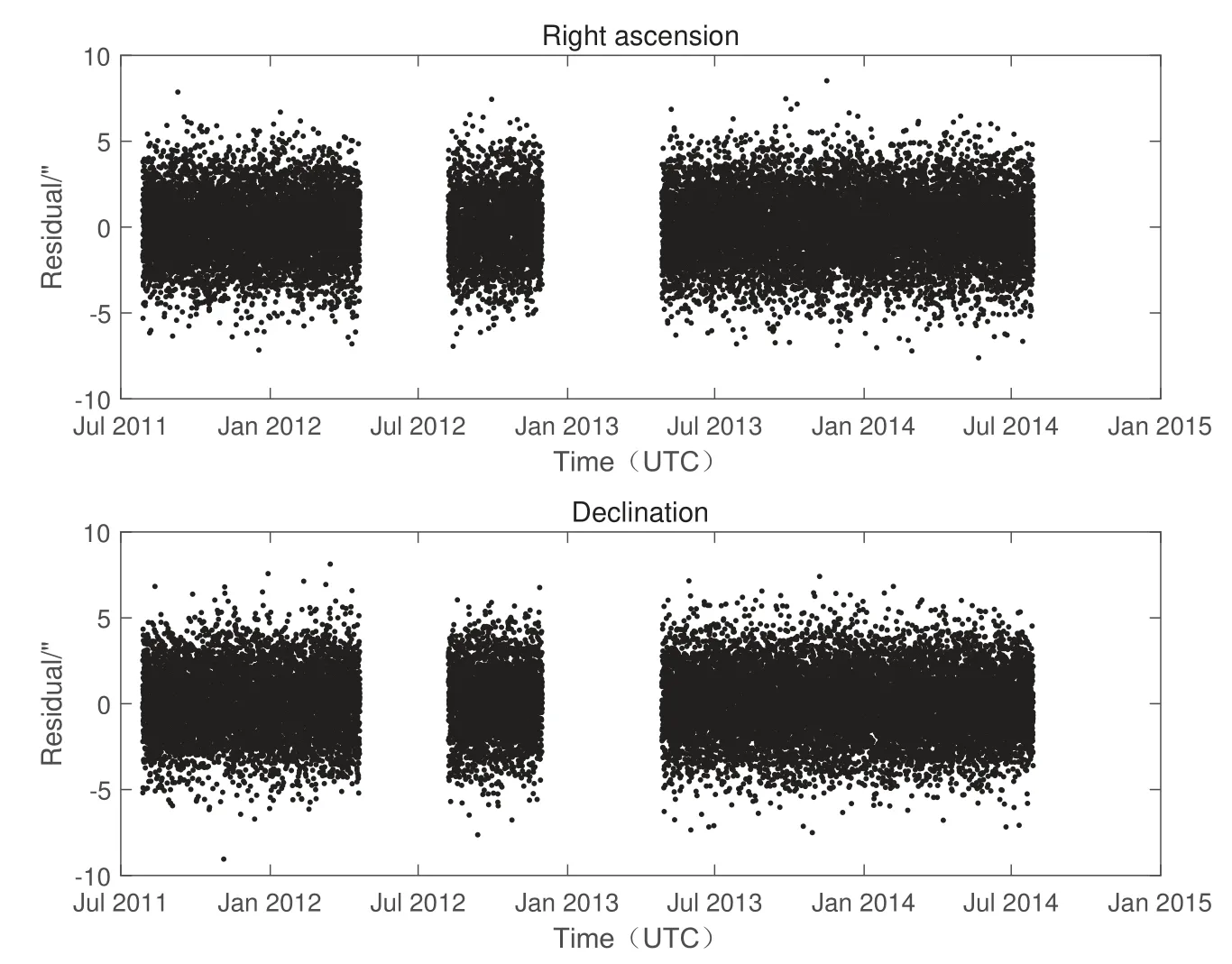
图10 续Fig.10 Continued

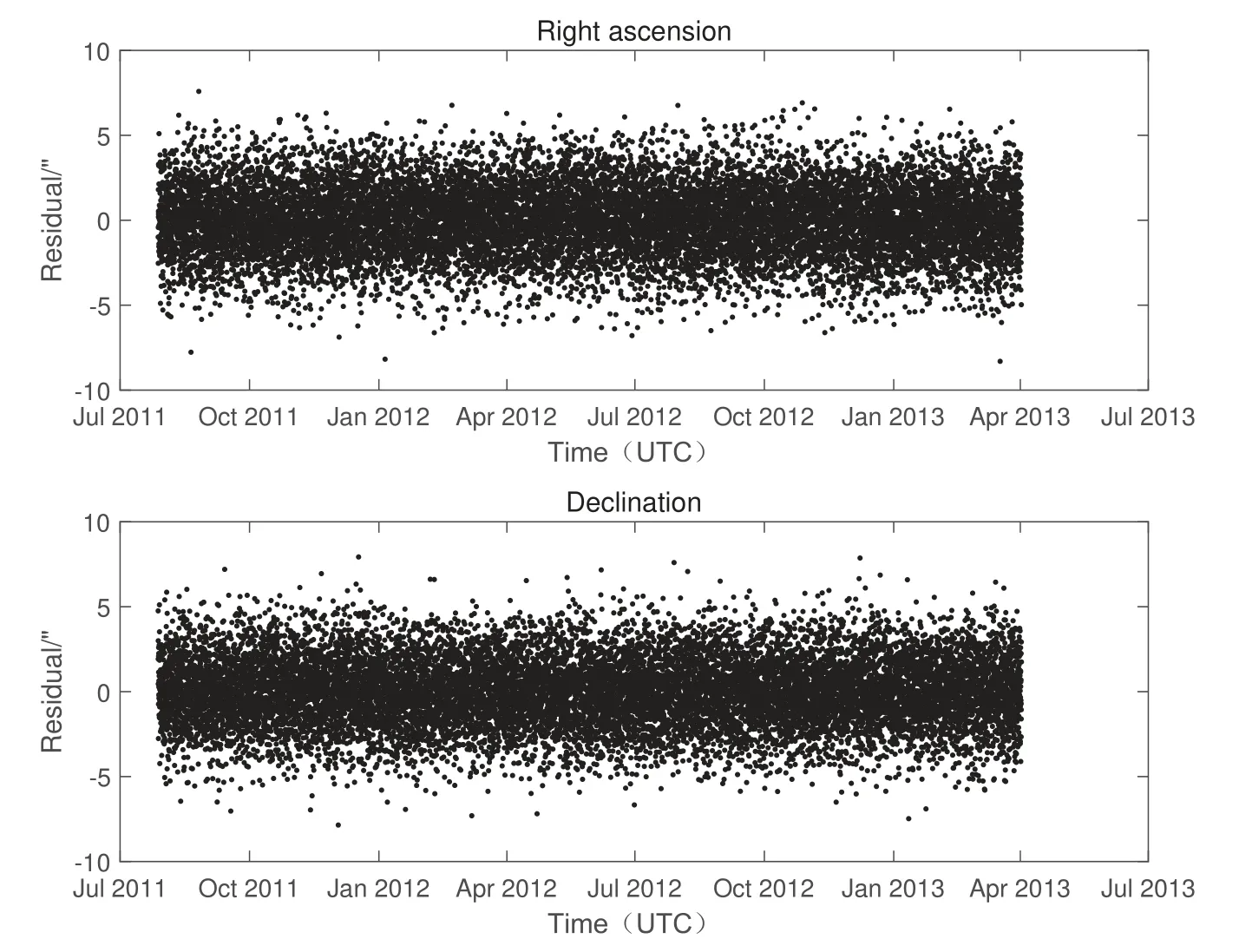
图10 双DRO对1951 RA测量3年的POD残差Fig.10 3-year POD residuals of dual DRO on 1951 RA

图11展示了在RTN坐标系下, 双DRO对1951 RA跟踪定轨所得轨道与仿真轨道的比较结果, 轨道精度大约在20 km左右.

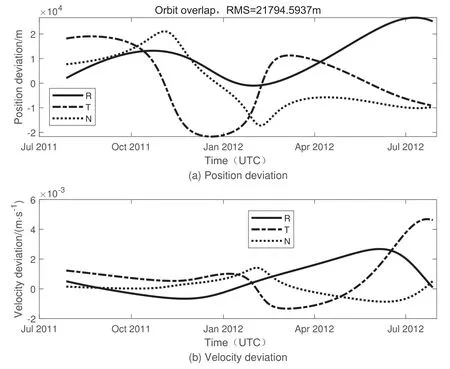
图11 双DRO对小行星1951 RA定轨与仿真轨道比较Fig.11 Comparison between orbit determination and simulated orbit of dual DRO on asteroid 1951 RA

5.3 DRO平台观测小行星2013 JX28

小行星2013 JX28在2016年第一次被发现, 是一颗轨道类型为Atira型的近地小行星,轨道周期为0.47 yr. 定轨弧段为2013年12月8日零时至2016年12月8日零时.

根据仿真条件, 仿真生成观测数据, 利用观测数据进行跟踪定轨, 定轨弧长3年单平台观测残差如图12所示.

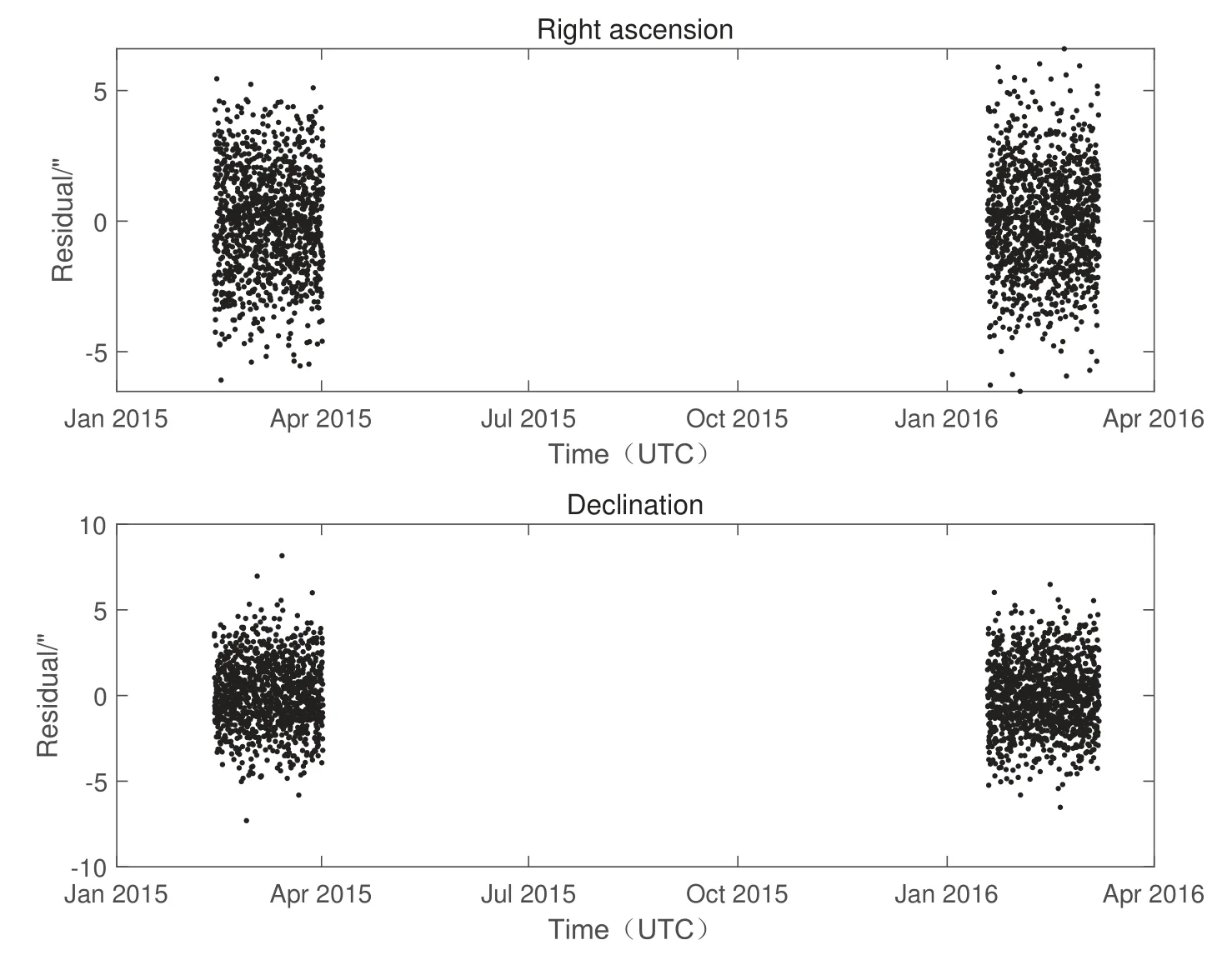
图12 单DRO对2013 JX28测量3年的POD残差Fig.12 3-year POD residuals of single DRO on 2013 JX28

图13给出了单DRO对小行星2013 JX28跟踪定轨与仿真轨道在RTN坐标系下的比较结果, 定轨精度大约为28 km左右. 图14给出了在相同仿真条件下, 双DRO平台观测小行星2013 JX28的残差图.

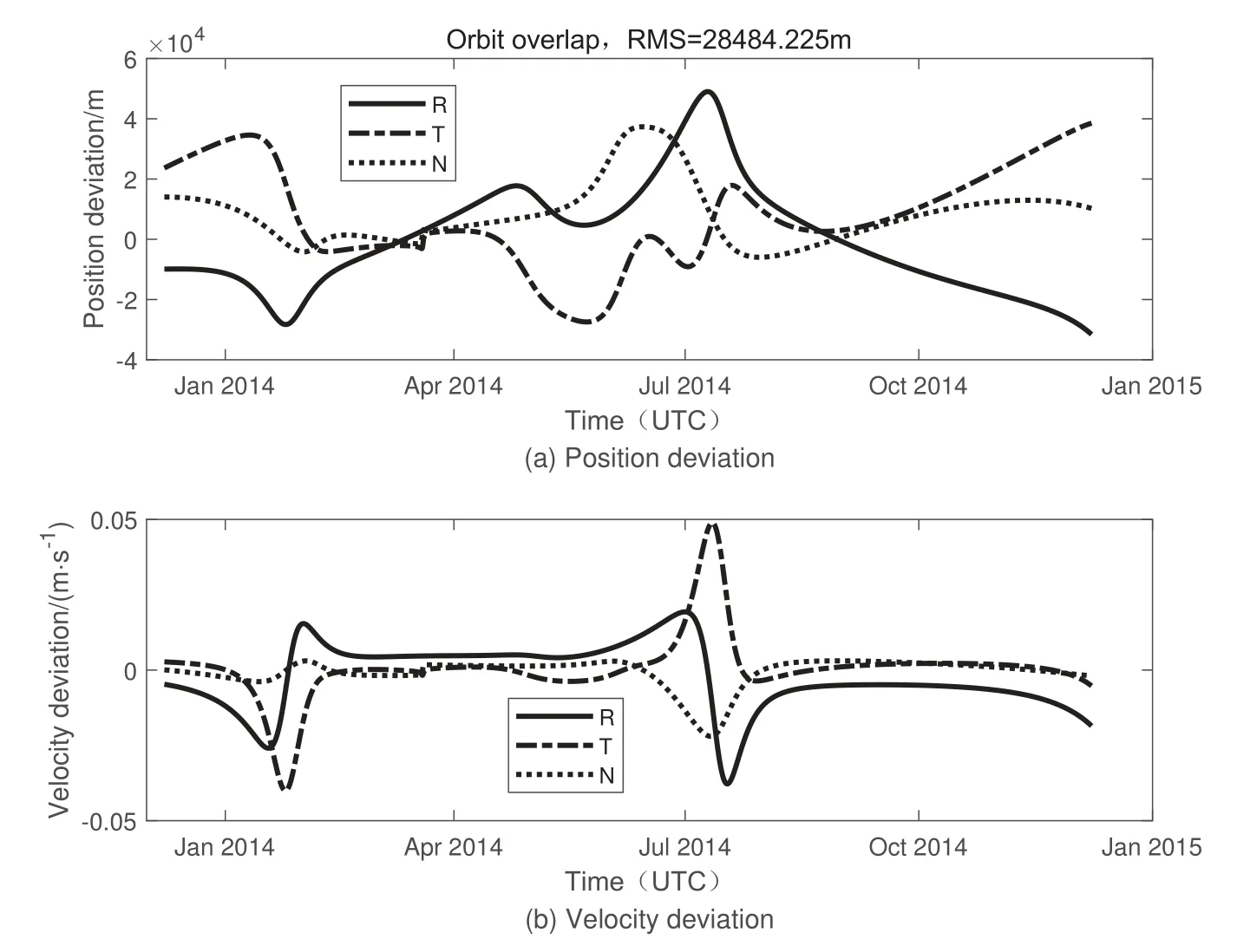
图13 单DRO对小行星2013 JX28定轨与仿真轨道比较Fig.13 Comparison between orbit determination and simulated orbit of single DRO on asteroid 2013 JX28

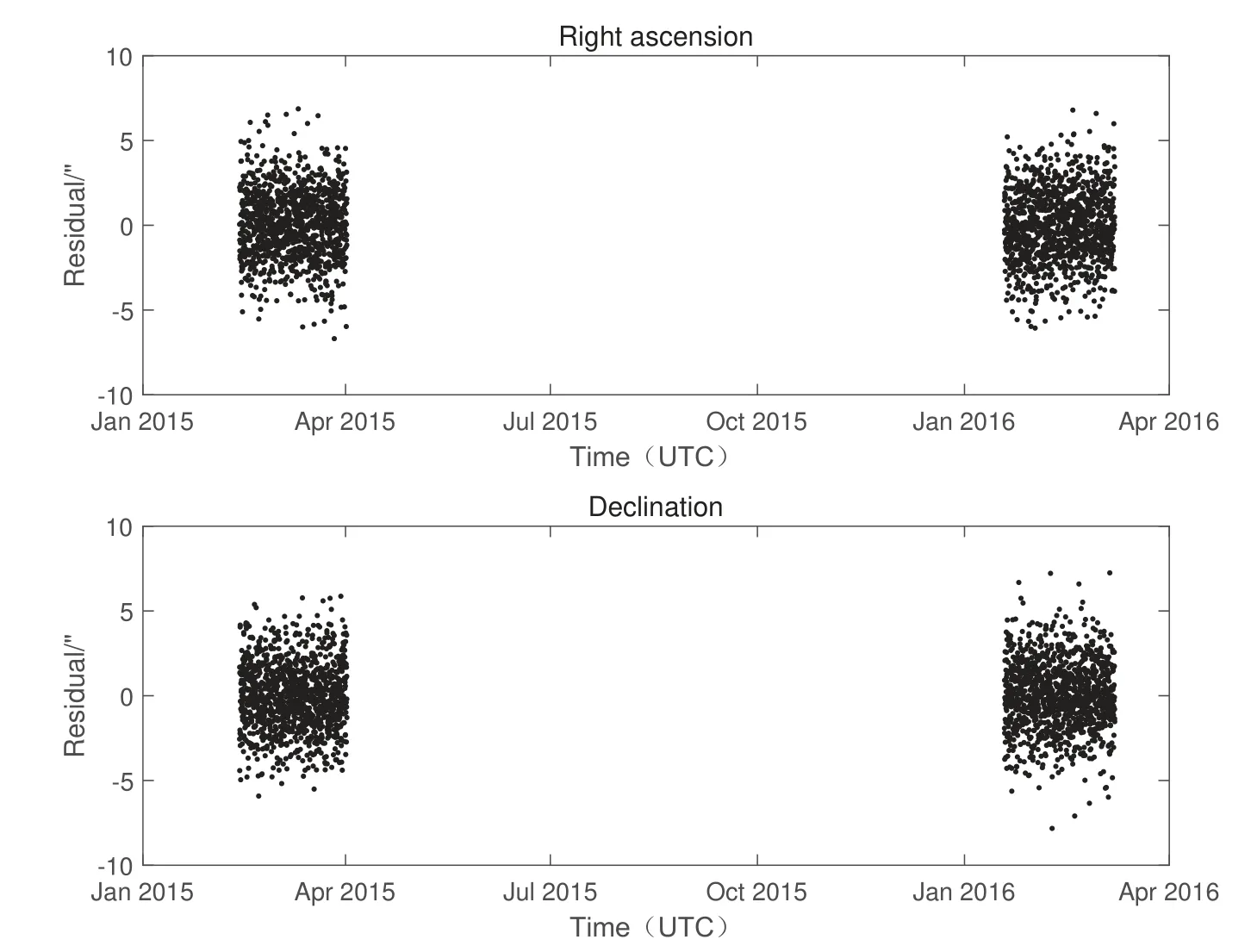
图14 双DRO对2013 JX28测量3年的POD残差Fig.14 3-year POD residuals of dual DRO on 2013 JX28

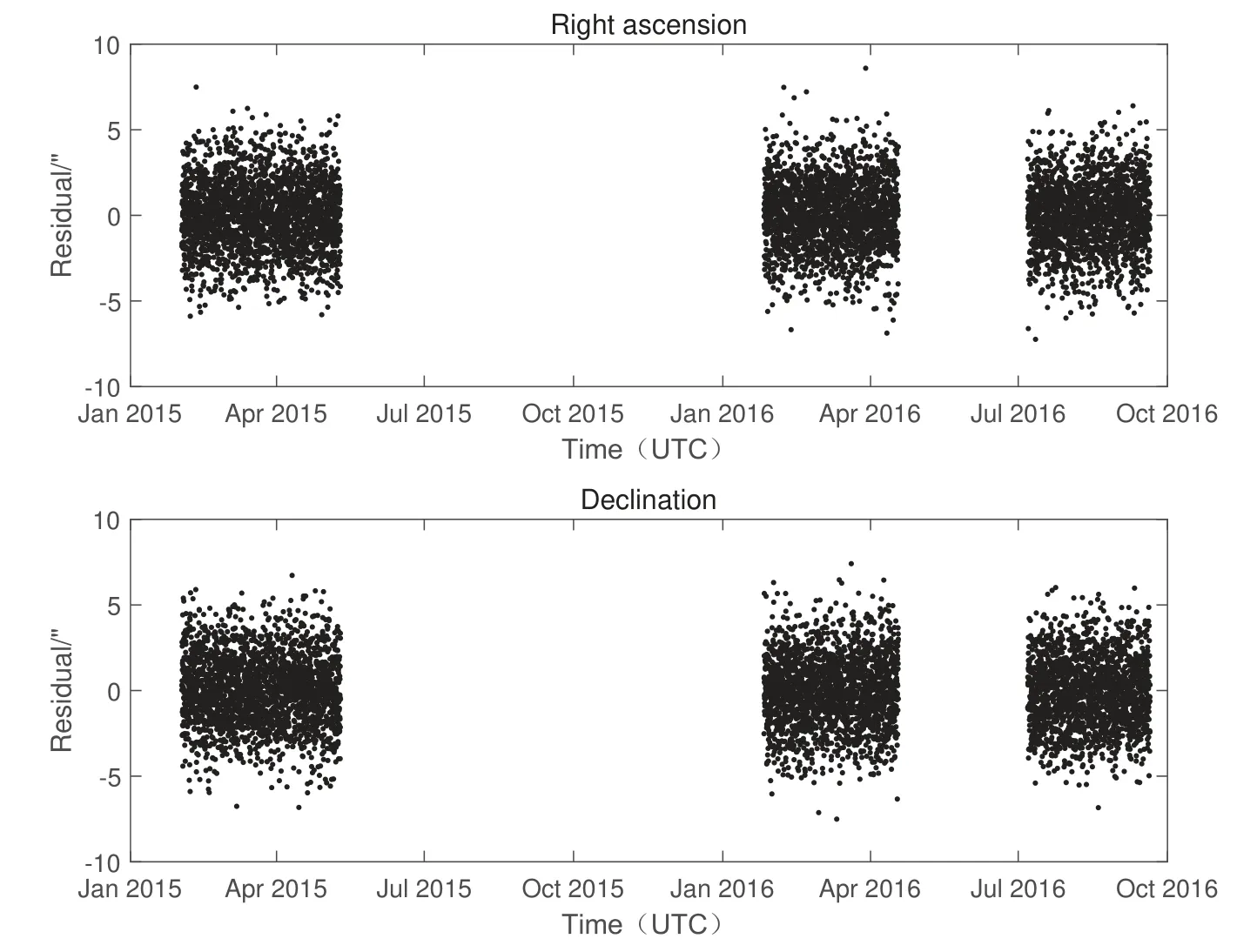
图14 续Fig.14 Continued

图15展示了在RTN坐标系下, 双DRO对2013 JX28跟踪定轨所得轨道与仿真轨道的比较结果,轨道精度大约在9 km左右.

5.4 DRO平台观测小行星1998 TU3

小行星1998 TU3由LINEAR在1998年10月13日发现, 是一颗轨道类型为Aten的近地小行星, 轨道周期为0.7 yr. 定轨弧段为2014年4月15日零时至2017年4月15日零时.

根据仿真条件, 仿真生成观测数据, 利用观测数据进行跟踪定轨, 定轨弧长3年单平台观测残差如图16所示.

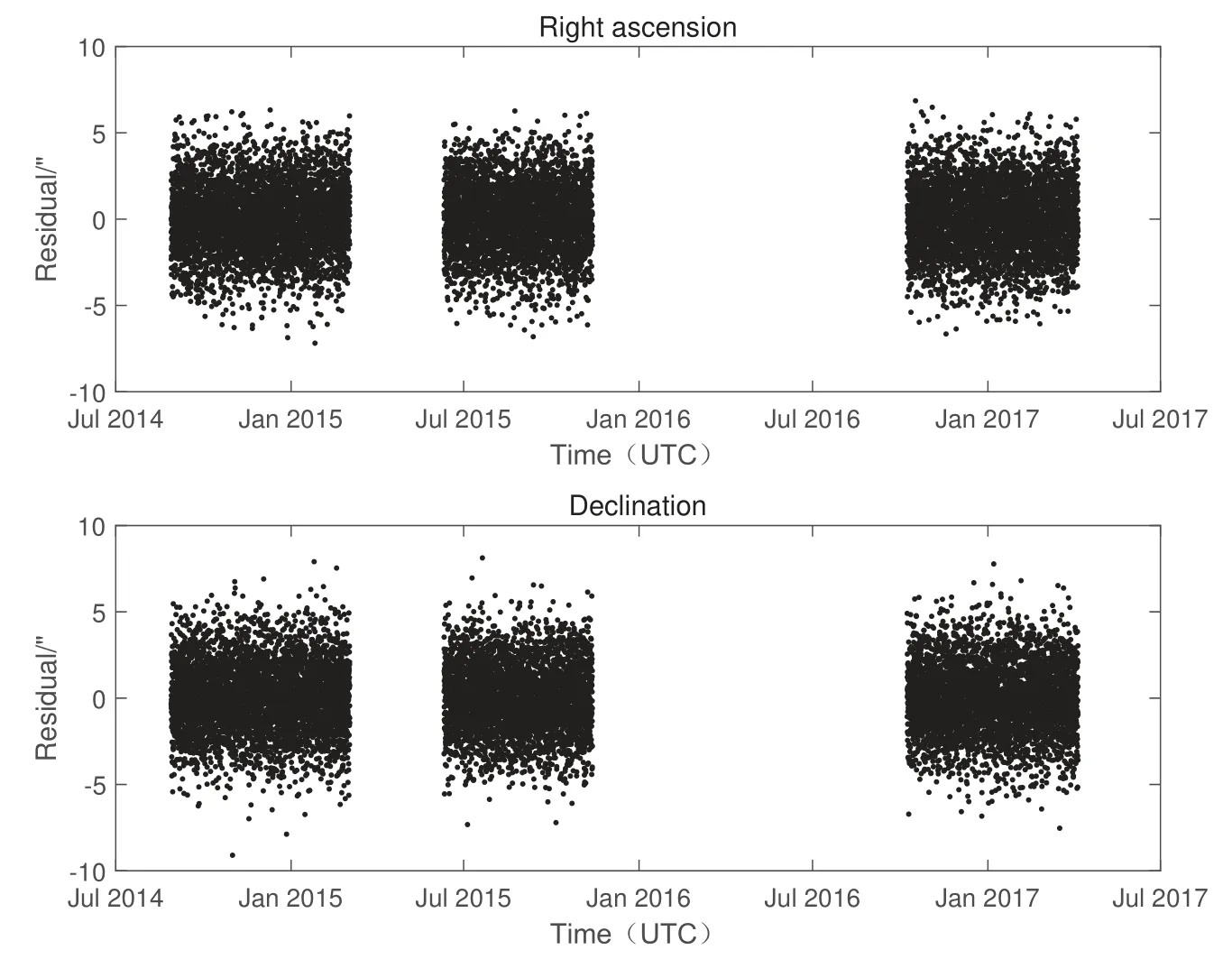
图16 单DRO对1998 TU3测量3年的POD残差Fig.16 3-year POD residuals of single DRO on 1998 TU3

图17给出了单DRO对小行星1998 TU3跟踪定轨与仿真轨道在RTN坐标系下的比较结果, 定轨精度大约为46 km左右. 图18给出了在相同仿真条件下, 双DRO平台观测小行星1998 TU3的残差图.

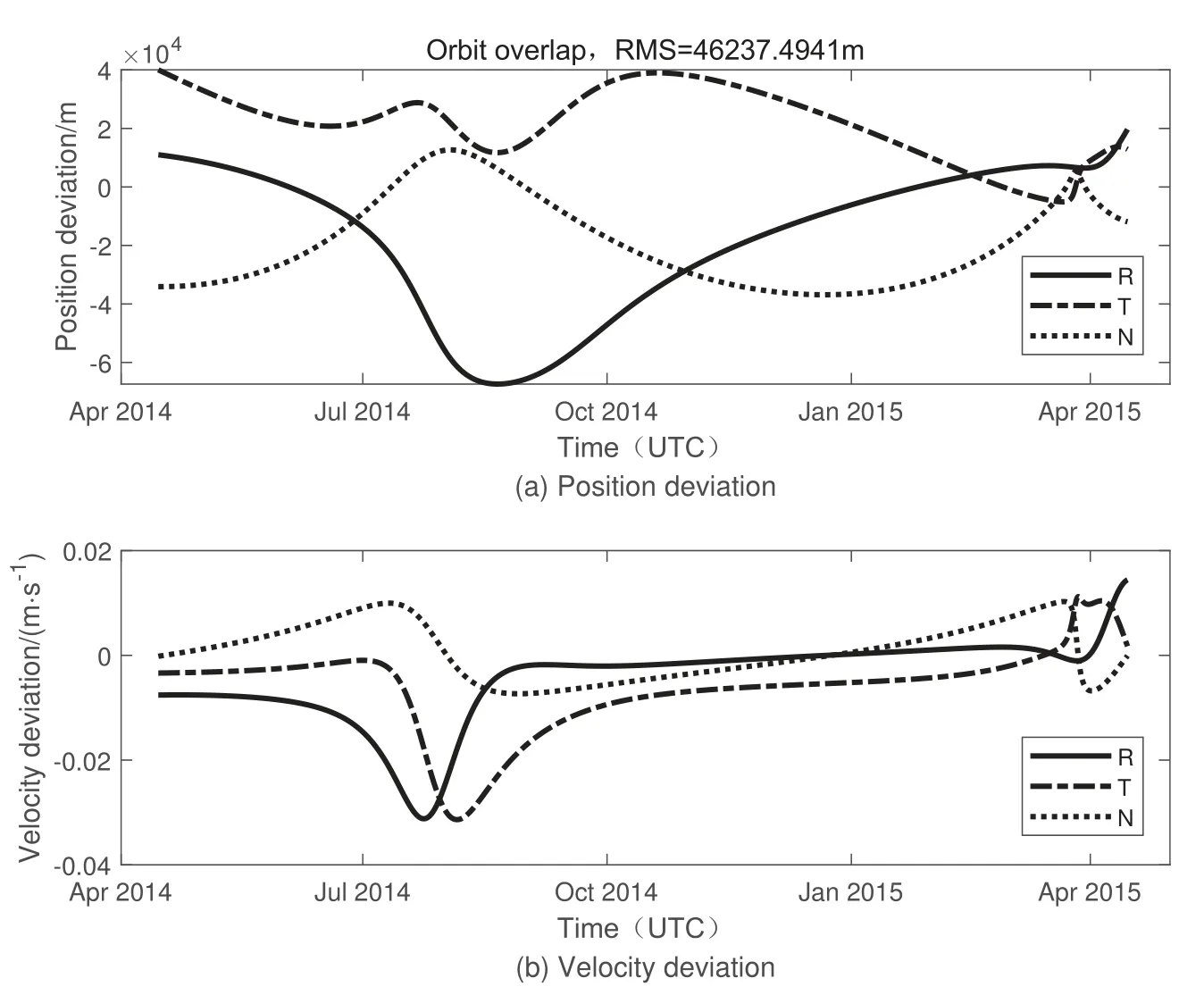
图17 单DRO对小行星1998 TU3定轨与仿真轨道比较Fig.17 Comparison between orbit determination and simulated orbit of single DRO on asteroid 1998 TU3

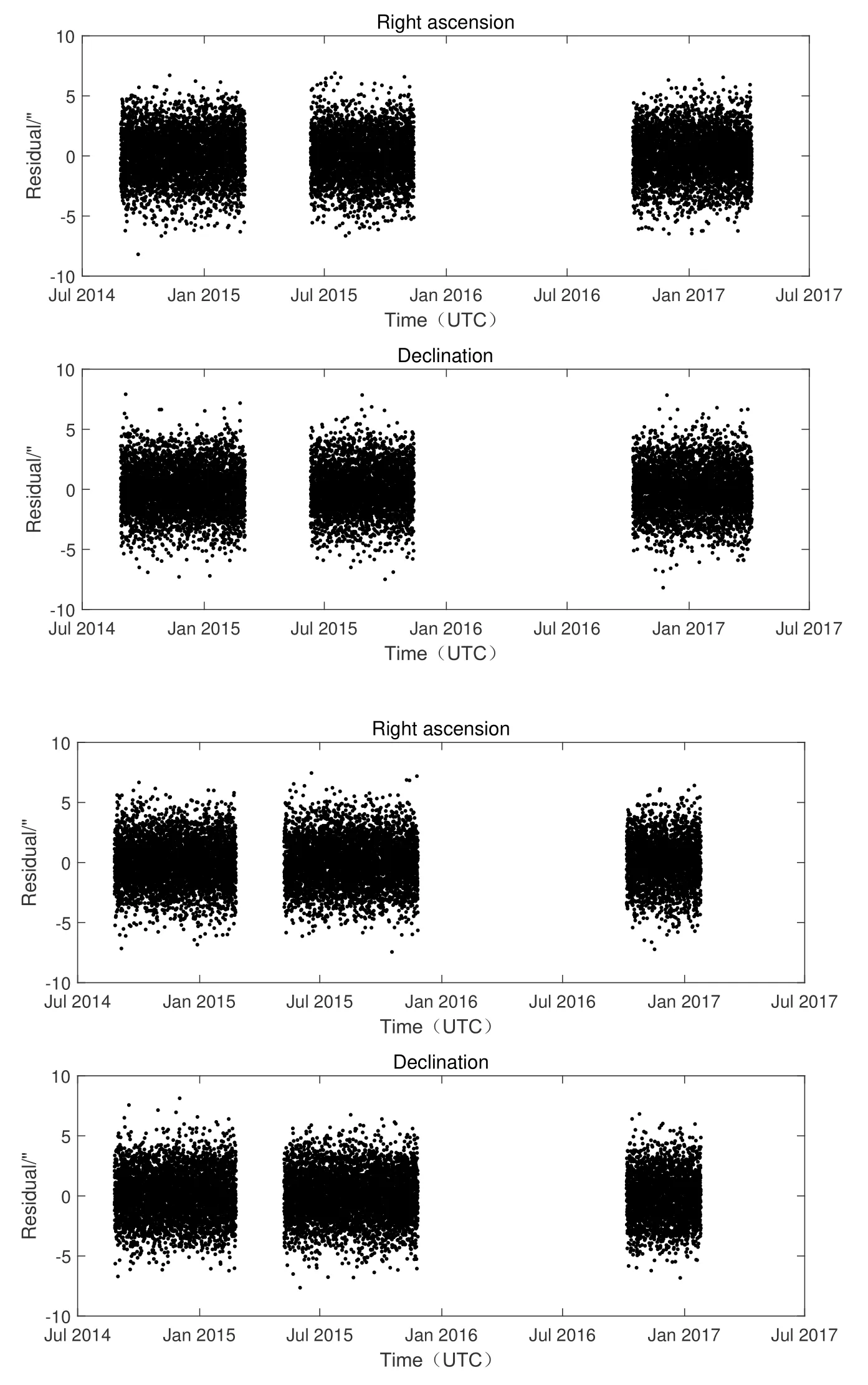
图18 双DRO对1998 TU3测量3年的POD残差Fig.18 3-year POD residuals of dual DRO on 1998 TU3

图19展示了在RTN坐标系下, 双DRO对1998 TU3跟踪定轨所得轨道与仿真轨道的比较结果, 轨道精度大约在29 km左右.

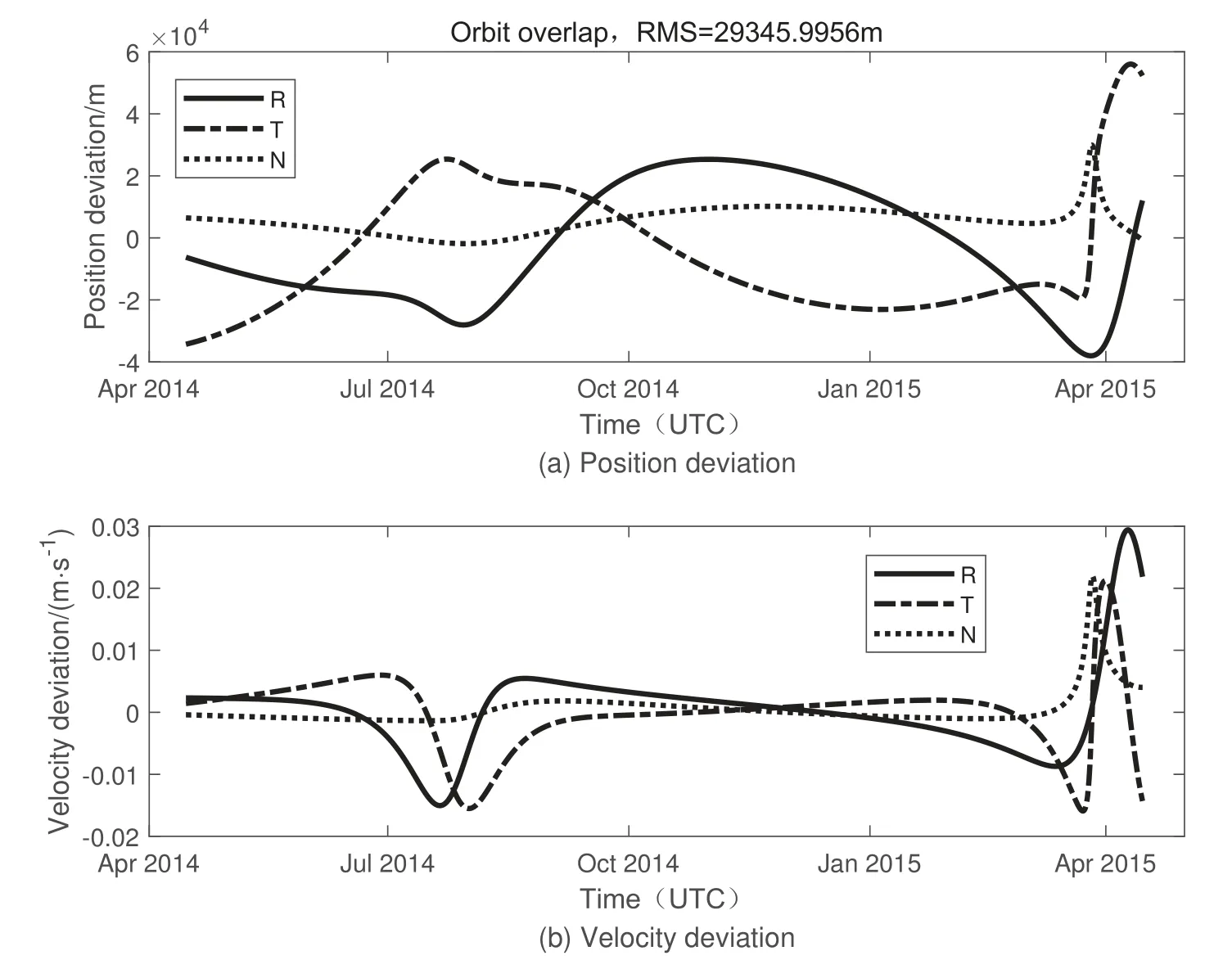
图19 双DRO对小行星1998 TU3定轨与仿真轨道比较Fig.19 Comparison between orbit determination and simulated orbit of dual DRO on asteroid 1998 TU3

综合以上仿真结果, 测角精度2角秒、数据采样间隔1 h、定轨弧长3 yr, 单DRO天基平台和双DRO天基平台对不同轨道类型的小行星进行轨道确定, 不同仿真算例中各台站的残差与仿真噪声大致相当, 定轨结果对比如表3所示.

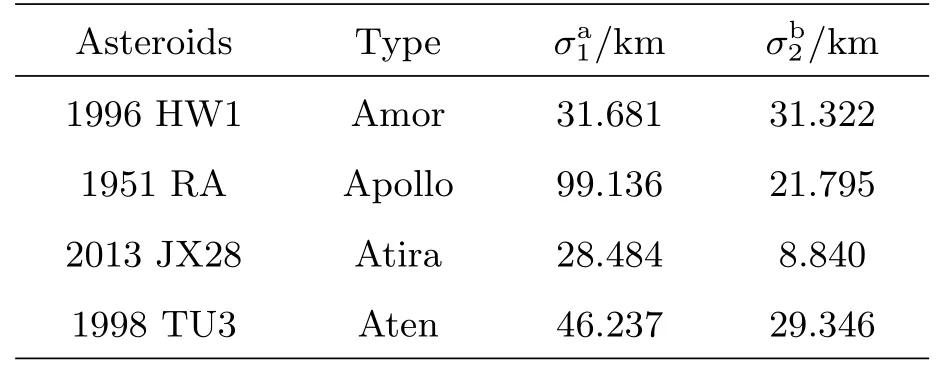
表3 数据采样间隔为1 h时的定轨结果统计Table 3 POD results statistics with 1 h data sampling interval

由表3可以看出, 对于Amor型小行星1996 HW1, 单DRO定轨精度和双DRO定轨精度无显著差异, 均在30 km左右; Apollo型小行星1951 RA和Aten型小行星1998 TU3, DRO天基平台数目由一个增加到两个时, 定轨精度改善明显, 可达30 km左右; Atria型小行星2013 JX28定轨精度最高, 双DRO定轨精度可达10 km以内, 定轨精度均满足一般的轨道监测需求.DRO天基平台对四类轨道类型的小行星的定轨精度不同, 主要原因是不同轨道类型的近地小行星与观测平台构造的观测几何不同,并且由于不同小行星运动周期不同, 导致观测弧长占整个轨道的比例也不同. 本文选择四类不同类型的小行星轨道进行计算分析, 具有一定代表性, 可以作为相关任务的初步参考. 在具体工程中, 不同小行星轨道确定精度会有一定差异. 本文还将数据采样间隔设为0.5 h, 在相同的测角精度和定轨弧长的仿真条件下, 单DRO天基平台和双DRO天基平台对不同轨道类型的小行星定轨精度如表4所示.

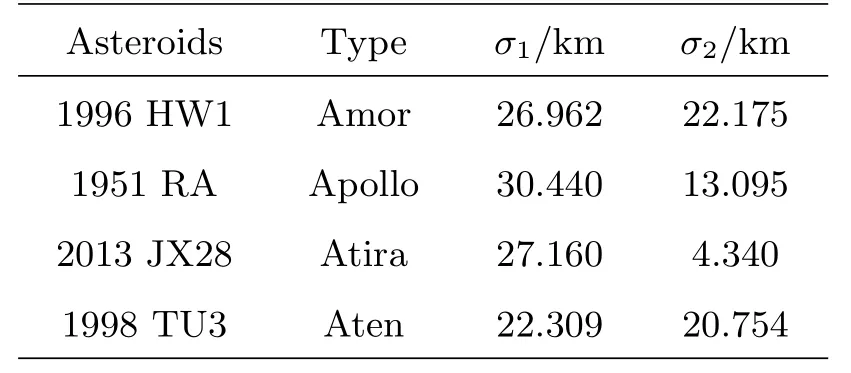
表4 数据采样间隔为0.5 h的定轨结果统计Table 4 POD results statistics with data sampling interval of 0.5 h

从表3和表4可以看出, 采样时间间隔会影响近地小行星的定轨精度, 相同的观测弧长下, 采样时间间隔越短获得的观测数据越多, 定轨精度也就越好. 但对于长期观测情况, 观测弧段足够长, 采样时间间隔对定轨精度不会有显著影响. 因此, 在一些情况下, 减小采样时间间隔可以提高定轨精度.

6 总结

本文针对地基跟踪观测近地小行星存在盲区的问题,提出了地月DRO星载光学测量对近地小行星进行轨道确定的方法. 通过光学可视性分析筛选仿真观测数据, 利用筛选得到的数据和JPL提供的小行星初轨信息, 采用数值法进行轨道确定.

对于不同轨道类型的近地小行星, 在数据采样间隔1 h、测量噪声2角秒的仿真条件下, DRO对目标天体的定轨精度不同.增加DRO观测平台的数量可有效提高Apollo型、Atira型、Aten型近地小行星的定轨精度, 其中Atira型小行星定轨精度最好,精度可达10 km以内. 同时采样时间间隔也会影响定轨精度, 减小采样时间间隔可以提高定轨精度.

地月DRO平台有效弥补地基光学监测系统监测盲区, 通过优化部署可对来自太阳方向的近地小行星实现更长时间的预警提前量, 对小行星的编目与监测预警具有一定意义.

致谢感谢国际小行星中心提供的在线数据下载服务和JPL/Horizons系统提供的在线历表服务.