脉冲星对氢原子钟的频率驾驭算法研究∗

韩孟纳 童明雷 李变

(1 中国科学院国家授时中心 西安 710600)

(2 中国科学院时间频率基准重点实验室 西安 710600)

(3 中国科学院大学天文与空间科学学院 北京 100049)

1 引言

时间频率技术的发展在国民经济、国防建设和基础科学中发挥着重要作用, 通信、互联网以及卫星导航等技术均需要建立精密、统一的时间系统. 为提供时间尺度服务, 美国海军天文台(United States Naval Observatory, USNO), 德国物理技术研究所(Physikalisch Technische Bundesanstalt,PTB),日本信息与通信技术研究所(National Institute of Information and Communications Technology, NICT), 中国科学院国家授时中心(National Time Service Center, NTSC)等均建立了自己的守时系统. 守时系统建立的目的在于实现统一的时间频率基准, 并保证基准的稳定性和准确性. 稳定性表征的是振荡器在一定时间内产生同样时间和频率的能力, 而准确性表征的是与理想值的关系, 时间基准的建立需同时兼顾准确度与稳定度[1].

国际原子时(International Atomic Time, TAI)系统是由全球共同维护的时间基准系统, 它是国际权度局(Bureau International des Poids et Mesures,BIPM)利用全球90多个时频实验室的500多台原子钟建立和维持的高精度时间系统. TAI由ALGOS算法[2]实现, 输入数据为全球实验室参与归算的原子钟与UTC (PTB)的比对钟差(此处UTC (Coordinated Universal Time)为协调世界时, UTC (k)代表实验室k保持的地方协调世界时), 比对方式为GPS (Global Positioning System)共视技术、卫星双向时间频率传递技术以及GPS载波相位时间传递技术.加权平均算法的关键是确定原子钟的权重,ALGOS算法属于典型的加权平均算法, 该算法中原子钟的权重采用月速率方差的倒数计算. 同时,为限制单台钟权值过大对原子时标造成不利的影响, ALGOS算法采用了最大权约束原则. 经加权平均计算后得到的原子时间尺度噪声水平会有效降低, 稳定度将高于单台原子钟.

实验室的原子钟包括守时型原子钟和基准型原子钟. 目前参与UTC计算的守时钟主要为氢钟和铯钟. 为更好地发挥氢原子钟优良的短期稳定度和低噪声特性, 从2014年开始, BIPM降低了铯钟参与TAI计算的总权重, 提升了氢钟的权重[3]. 截至2021年12月, 氢钟在计算自由时标(´Echelle Atomique Libre,EAL)中所占的权重达到了85%左右,成为UTC保持的核心守时钟. 由于氢钟的精度不断提高, 绝大多数实验室的主钟频率源由铯钟更换为氢钟. 2005年3月起, 国家授时中心采用氢钟做主钟.对氢钟开展相应的研究, 有望进一步提高本地时间尺度的性能.

地球时(Terrestrial Time,TT)作为一种理想的时间尺度, 其时间单位与大地水准面上的国际单位制(Syst‵eme International d’Unit´es, SI)秒一致, 原点定义为在1977年1月1日零时(TAI), TT=TAI+32.184 s. TAI为TT的一种实现, 考虑到实时性需求, TAI每月归算一次, 因此TT (TAI)的精度在一定程度上受到影响. 且由于主频标的不确定度以及频率驾驭过程的不完美, TAI存在长期的频率波动. 此外, TAI还存在季节性波动[4]. 为克服TT(TAI)的上述缺陷, BIPM利用了所有可用的基准钟的数据, 在计算过程中进行了黑体辐射频移改正,并对EAL与TT间的频率偏差进行低通滤波与插值处理, 扣除了EAL频率的周年项与长期变化项, 最终得到TT的最优实现–TT (BIPM)[5]. TT (BIPMXX)每年归算一次, XX为年份的后两位数字.

TT (BIPM)的钟差数据发布周期为一年, 影响时间比对的实时性, 而脉冲星有望在缺失比对数据的情况下保证本地时间的准确性. 脉冲星自转非常稳定, 其旋转产生的周期性脉冲信号可被地面射电望远镜接收. 这种稳定的周期信号可作为一种天然的频率源, 称为脉冲星钟[6–7]. 毫秒脉冲星自转的长期稳定度可媲美高精度的原子钟,利用参考钟对所有脉冲星计时残差影响相同的特性, 可构建综合脉冲星时间尺度(Ensemble Pulsar Timescale, EPT)[8–9]. EPT是同时观测多颗毫秒脉冲星, 并设计相应的算法提取计时残差的公共信号得到. EPT可用于检验原子时的长期波动[10],并作为TT的一种新的实现方式, 记为TT (PT),PT (Pulsar Time)为脉冲星时. 原子时的建立与脉冲星时的建立属于两个完全不同的物理过程,而TT (PT)与TT (BIPM)的差异很小[11–12], 因此其他时间尺度相对于TT (BIPM)的波动可利用TT(PT)加以检验.

本地时间UTC(k)是基于单台物理钟产生的时间信号, 而任何一台物理钟相对于标准时间尺度均存在钟速, 因此需要对主钟进行频率驾驭. 目前,各实验室利用BIPM前期发布的UTC (k)与UTC的时刻差, 推算出相位微调和频率微调的数据, 进而对UTC (k)加以控制. 但BIPM发布数据的滞后将对UTC(k)的准确性产生影响.作为TT的另一种实现, 我们尝试用TT (PT)长期驾驭主钟频率.

为了监测和改善伽利略系统时间的长期稳定性, 2018年12月, 欧空局位于荷兰的技术中心开始运行基于脉冲星时驾驭伽利略卫星导航系统主控站主钟的“Pulchron” (Pulsar Chron)项目[13]. 基于此项目与五百米口径球面射电望远镜FAST (Fivehundred-meter Aperture Spherical radio Telescope)等国内望远镜的高灵敏度观测, 周庆勇等人给出了可提高北斗卫星导航系统时间基准长期稳定性的中国脉冲星时地面服务系统(China Pulsar Time Ground Service System, CPTGSS)的构建方案[14]. 目前脉冲星的观测通常利用脉冲星计时阵列开展, 国际上主要的脉冲星计时阵包括澳大利亚Parkes脉冲星计时阵PPTA (Parkes Pulsar Timing Array)、北美纳赫兹引力波计时阵NANOGrav(North American Nanohertz Observatory for Gravitational Waves)以及欧洲脉冲星计时阵EPTA (European Pulsar Timing Array), 三者共同组成了国际脉冲星计时阵IPTA(International Pulsar Timing Array). IPTA的主要科学目标为探测甚低频引力波以及建立脉冲星时间尺度, 其对毫秒脉冲星脉冲到达时间TOA (Time of Arrival)的典型测量精度达到几百纳秒. 本文从IPTA第二批发布数据IPTA2中选取了4颗计时精度较高的毫秒脉冲星(J0437-4715、J1713+0747、J1744-1134、J1909-3744)约6.2 yr的实测数据, 对四颗星的稳定度进行分析. 选取的研究对象为NTSC的一台主动型氢脉泽钟(H1404926), 钟差数据来源于BIPM网站1https://webtai.bipm.org/ftp/pub/tai/data/.. 基于此钟的钟差数据, 本文给出了利用毫秒脉冲星观测数据每三个月、每半年和一年为周期驾驭一次主钟频率的方法, 并对四颗星的综合驾驭能力进行评估.

2 四颗脉冲星稳定度评估

本文首先对IPTA2的实测数据[15]进行处理, 得到四颗星的拟合前计时残差, 该过程涉及一系列的时间尺度转换. 实际记录TOA的钟为测站的本地钟, 为扣除参考钟对脉冲星计时精度的影响, 本地钟的读数需转到TT (BIPM)时间尺度[4]. 此外, 为扣除几何时延、光线弯曲、大气传播时延、视差效应以及狭义相对论的“动钟变慢”、广义相对论中的“引力红移”对不同位置钟的走速影响等因素,TOA需最终转到太阳系质心坐标时TCB (Barycentric Coordinate Time)[16–17]. 脉冲星的计时模型参数通过拟合计时残差获得, 可用于在太阳系质心SSB (Solar System Barycenter)处预报TOA. 计时残差为脉冲实际到达时间与模型预报时间的差值, 一般在TCB时间尺度下计算. 采用Tempo2脉冲星数据处理软件[18]对四颗星的观测数据重新进行模型参数拟合, 最终得到四颗星的拟合后计时残差如图1所示, 图中MJD (Modified Julian Date)为约化儒略日. 为与下文氢钟钟差数据的时间区间一致, 对观测数据进行截取, 截取后数据的时间跨度为MJD: 53739–56014. 从计时残差结果来看, 除脉冲星J0437-4715, 其他三颗星的计时残差均在零附近波动, 说明这三颗星不含明显的计时噪声.

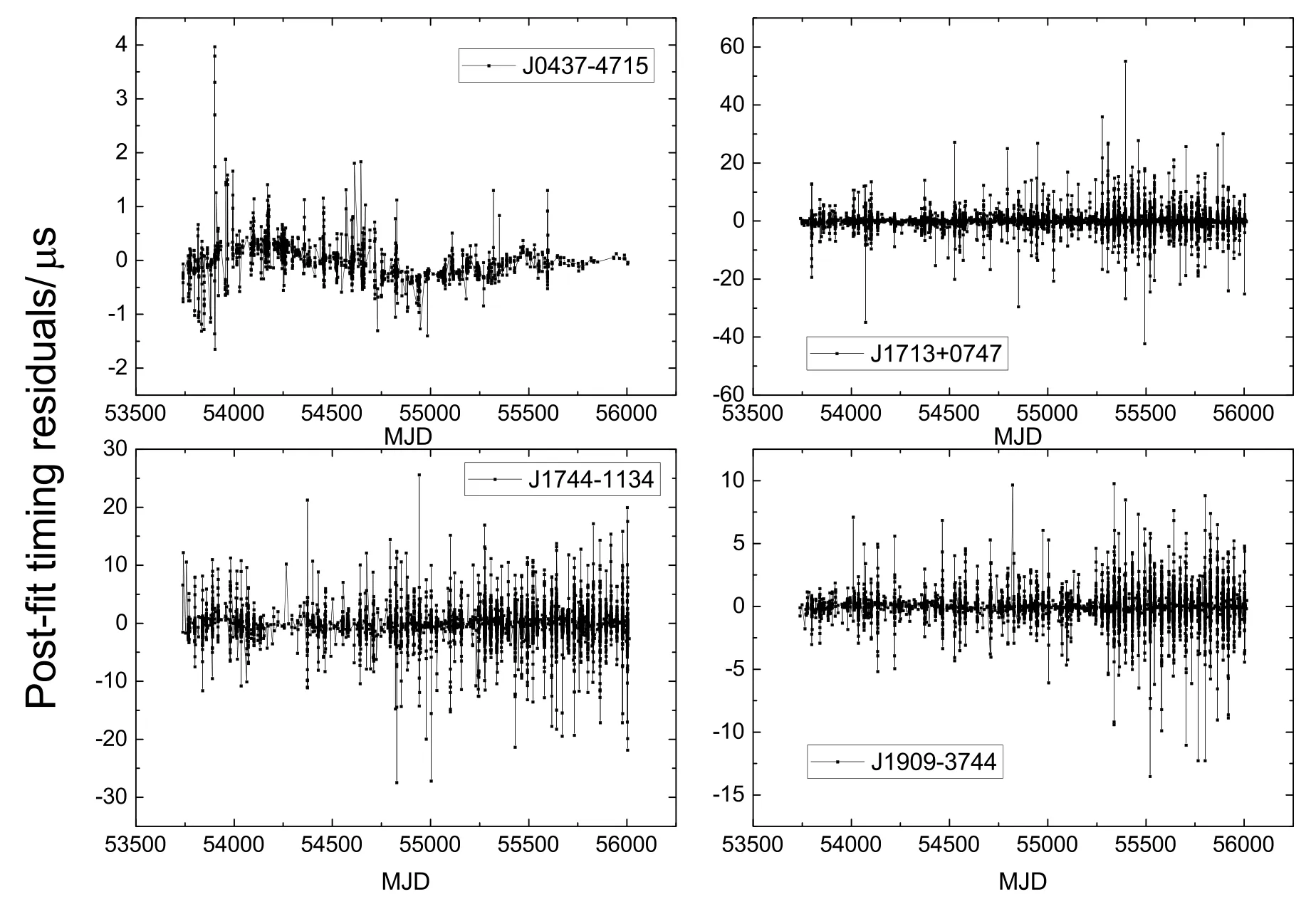
图1 四颗脉冲星的拟合后计时残差图Fig.1The post-fit timing residuals of four pulsars

脉冲星的稳定度采用Matsakis等人提出的统计量σz表征[19], 其不要求数据的等间隔分布, 适用于脉冲星观测数据的分析.σz按照下式计算:

其中,c3为对长度为τ的观测数据进行三次多项式函数拟合得到的三次项系数; 式中的尖括号表示加权平均, 权重为拟合值c3不确定度的平方倒数. 采用上式分别计算脉冲星的稳定度, 得到四颗星的稳定度随时间的变化关系如图2所示. 对四颗星的稳定度结果进行分析, 可以看出脉冲星的稳定度随着时间增加, 即其具有优良的长期稳定度. 四颗星整体稳定度均大致服从lgσz ∝lgτ(µ=-3), 上述关系对应图2中斜率为-1.5的直线, 说明四颗脉冲星的主要噪声类型为白噪声. 对于观测时间小于一年的数据, PSR J1744-4715的稳定度略逊色于其他三颗星. 四颗脉冲星(J0437-4715、J1713+0747、J1744-1134、J1909-3744)约6 yr观测数据的稳定度分别为7.95×10-15、4.38×10-16、4.94×10-15、3.66×10-16. 随着观测设备灵敏度的增加, 四颗星观测数据的稳定度均得到进一步的提高.

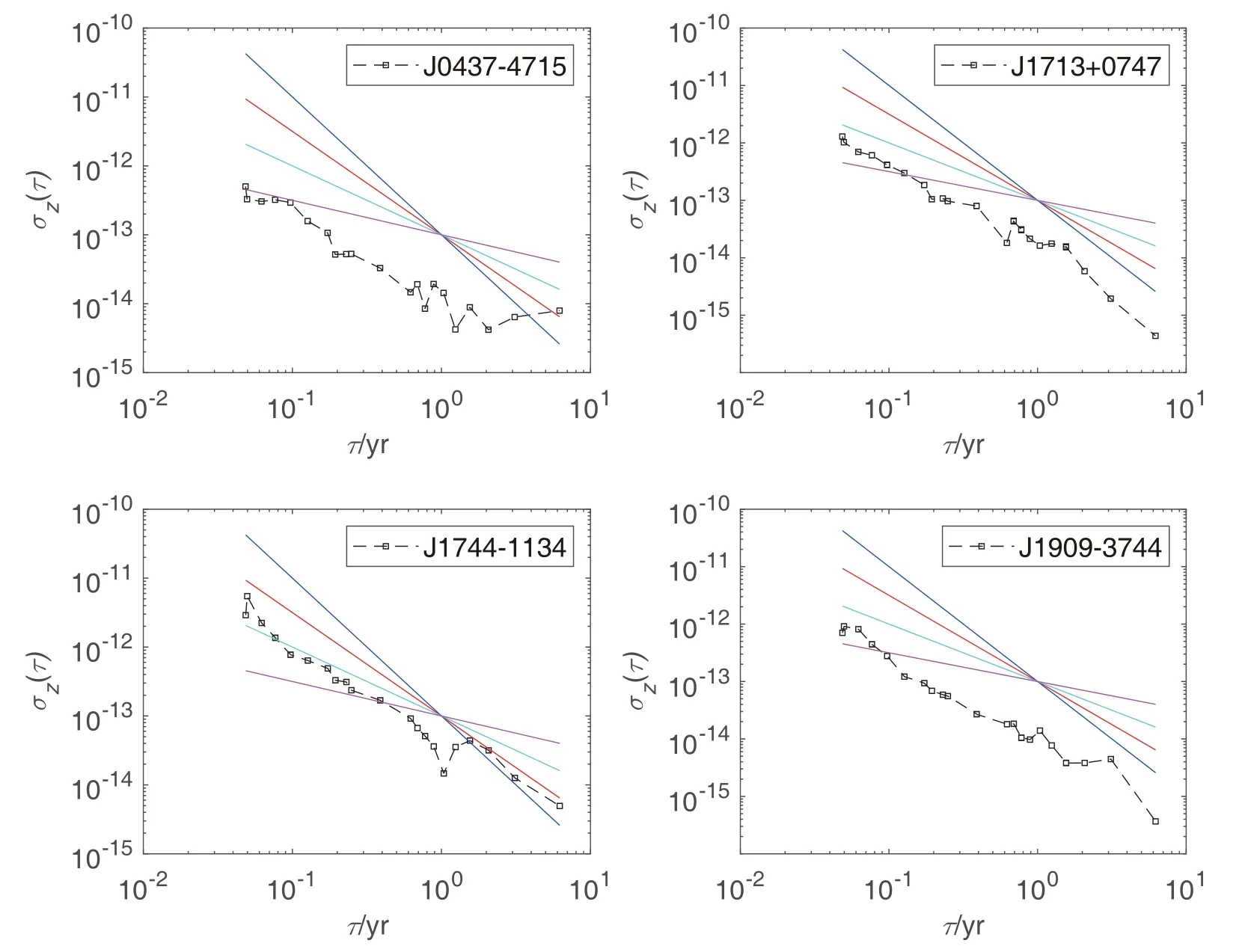
图2 四颗脉冲星的稳定度随时间的变化图. 图中颜色不同的直线斜率不同, 蓝色、红色、青色、洋红色线的斜率分别为-2、-1.5、-1、-0.5.Fig.2 Variation of the stability of four pulsars with time. The slopes of the blue, red, blue-green and purple lines are -2, -1.5,-1 and -0.5, respectively.

3 脉冲星驾驭原子钟

NTSC的守时钟组包括主动型氢钟和铯钟, 主动型氢钟的短期稳定度优于铯钟. 若能利用脉冲星准确预报氢钟的频率偏差及频率漂移并将其扣除,有望提高时间尺度的长期稳定度. 时间实验室负责产生和保持的系统时间包括物理时间和纸面时间.对于物理时间, 可利用毫秒脉冲星的计时信息控制主钟频率, 实时输出物理信号; 纸面时间需要利用历史数据重新进行原子时的计算, 以达到更高的稳定度, 属于事后计算. 本文主要针对主钟的实时物理信号驾驭开展相应的研究.

为提高实时UTC (k)信号的准确性, 可利用守时钟组、快速UTC (UTCr)与UTC分别实现对主钟频率的每日、每周及每月驾驭[20–21]. 为提高氢钟长期保持的准确性, 本文提出在上述驾驭方法的基础上, 增加利用毫秒脉冲星的观测数据定期驾驭氢原子钟的方案. 下文首先研究了NTSC一台参与TAI归算的氢钟H1404926 (H代表原子钟类型为氢钟, 1404926为钟编号)的稳定度, 然后给出利用脉冲星驾驭氢钟的方法.

3.1 氢钟稳定度分析

氢钟具有优良的短期稳定度, 充分发挥氢钟的特性对于地方协调世界时UTC(k)的高精度保持具有重要意义. 图3给出了利用哈达玛方差[22]计算的氢钟H1404926的稳定度,从图中可以看出氢钟的短稳高而长稳较差, 这主要由氢钟的老化引起. 哈达玛方差采用了频率数据的二阶差分、相位数据的一阶差分, 其对调频闪烁游走噪声和调频随机奔走噪声收敛, 且对于线性频率漂移不灵敏, 因此适用于氢钟的稳定度分析. 针对相位数据哈达玛方差的定义为:

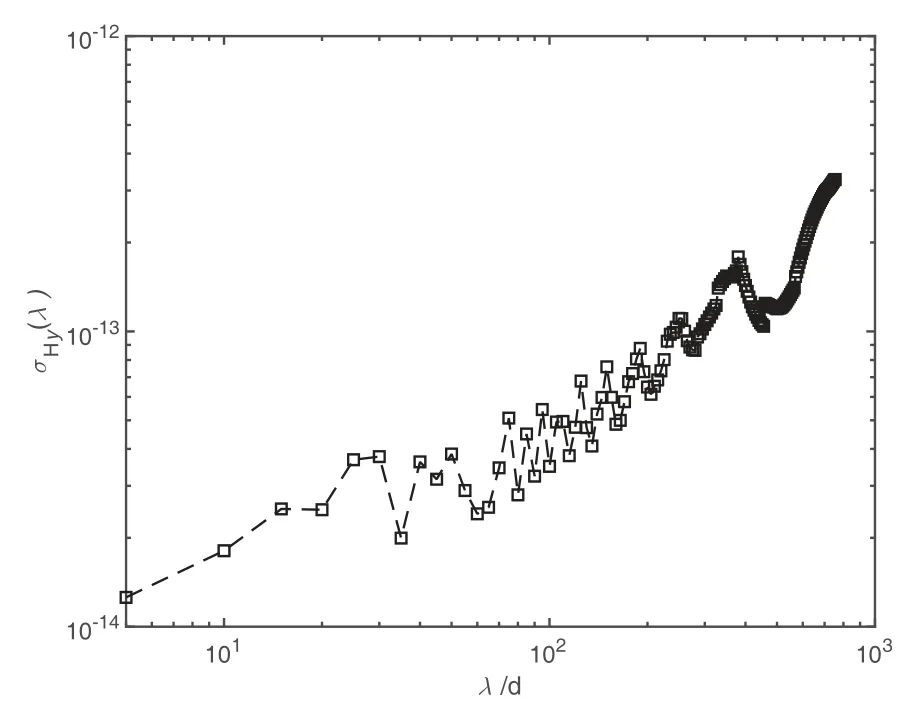
图3 哈达玛偏差表征的氢钟稳定度随时间的变化图Fig.3 The variation of stability of the hydrogen master with time characterized by Hadamard deviation

其中,xi、xi+1、xi+2、xi+3为连续的相位数据, 相邻数据间的时间间隔为λ.N为相位数据的取样数.通常使用哈达玛方差的平方根, 即哈达玛偏差表征氢钟的稳定度.

记单台原子钟实现的TT为TT (Y), 其中Y为原子钟的编号. 将本文使用的氢钟实现的TT记为TT(H1404926), 即TT(H1404926)=H1404926+32.184 s. 利用BIPM发布数据, 经下式转换可以得到真实钟差TT (H1404926)- TT (BIPM),

钟差结果如图4所示, 从图中可以看出二者之间存在频率漂移, 可见单台钟实现的TT是不准确的.

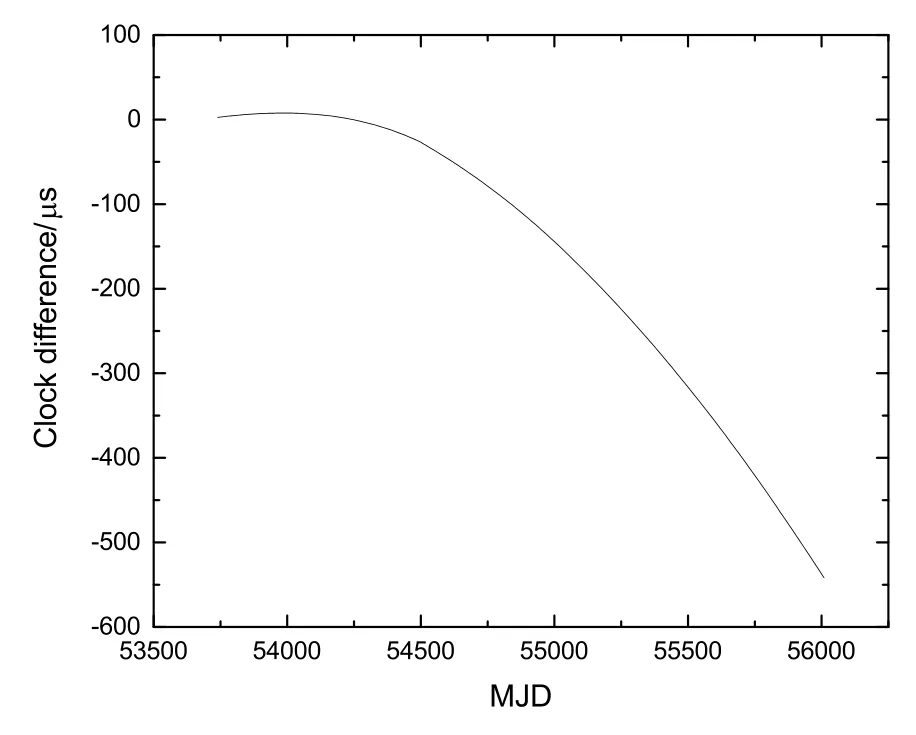
图4 TT (H1404926)与TT (BIPM)之间的真实钟差Fig.4 The real clock difference between TT (H1404926) and TT (BIPM)

与铯钟不同, 氢钟存在频率漂移, 氢钟的预报模型采用二次三项式[23], 即:

这里,h(t)为t时刻氢钟时刻预报值,A为t0时刻的钟差,B、C分别为钟的频率偏差以及频率漂移.对TT (BIPM)与氢钟之间的真实钟差每月进行二次三项式拟合, 得到氢钟的频率偏差不是常数, 而是随时间变化的.

国家授时中心采用类ALGOS算法计算本地时间, 多台原子钟的读数经加权平均算法得到自由时标后, 结合BIPM网站发布的钟差数据计算驾驭量, 对主钟频率进行驾驭. 脉冲星对氢钟的驾驭只需在记录TOA的参考钟与守时原子钟之间建立时间比对网, 也可通过参考共同的时标, 如北斗导航卫星的系统时间(BeiDou Time, BDT), 使二者建立联系. 此外, 可将脉冲星实现的TT (PT)作为TT(BIPM)的一种检验方式, 并在BIPM的比对数据更新不及时的情况下维持本地时间的准确性. 下面我们利用脉冲星对氢钟分别以三个月、半年、一年为周期进行驾驭.

3.2 脉冲星钟对氢钟的频率驾驭方法

通过设计参考钟与主钟系统频率源之间的比对链路, 可实现脉冲星对主钟频率的驾驭, 以此提高本地时间系统的准确性. 若参考钟无钟差、模型参数准确且脉冲星不存在计时噪声, 则拟合前计时残差将呈现出均值为零的白噪声特征. 为研究脉冲星对氢钟的驾驭结果, 本文将TOA的参考时间尺度转换为TT (H1404926). 由于计时残差是在TCB尺度下计算得到的, 因此, 拟合前计时残差应为TT(H1404926)相对于TT (PT)的变化在TCB时间尺度下的对应值.为得到TT(H1404926)-TT(PT),需计算TT与TCB之间的比例关系. TCB与地心坐标时TCG (Geocentric Coordinate Time)之间的差异包括周期项与长期漂移项, 即[24]:

其中LC=1.480826867×10-8,TTl为线性项,TTn为非线性项, ∆b为观测者依赖项. TT与TCG的速率之比为一常数, 即TT与TCB的走时速率存在如下关系:

其中LB= 1.550519768× 10-8. 从上式可知, 若将TCB时间尺度下氢钟的频率偏差记为l, 即TCB(H1404926)- TCB (PT)的斜率, 则在TT时间尺度下氢钟的频率偏差为l(1-LB). 该速率差远小于脉冲星对氢钟频率偏差的估计误差10-15, 因此对估计结果的影响可以忽略.

TOA以TT (H1404926)为参考时, 得到四颗星的拟合前计时残差如图5所示, 脉冲星数据长度约6.2年. 其变化趋势基本与图4中真实钟差的趋势一致, 证实了脉冲星驾驭原子钟的可行性. 从图5可以看出, 以同一台氢钟为参考钟记录TOA时, 四颗脉冲星的拟合前计时残差变化趋势一致; 但由于每颗星本身的计时噪声不同, 因此各星计时残差中随机项的波动程度不同, 下文采用抗差估计[26–27]降低脉冲星计时噪声对驾驭结果的影响.

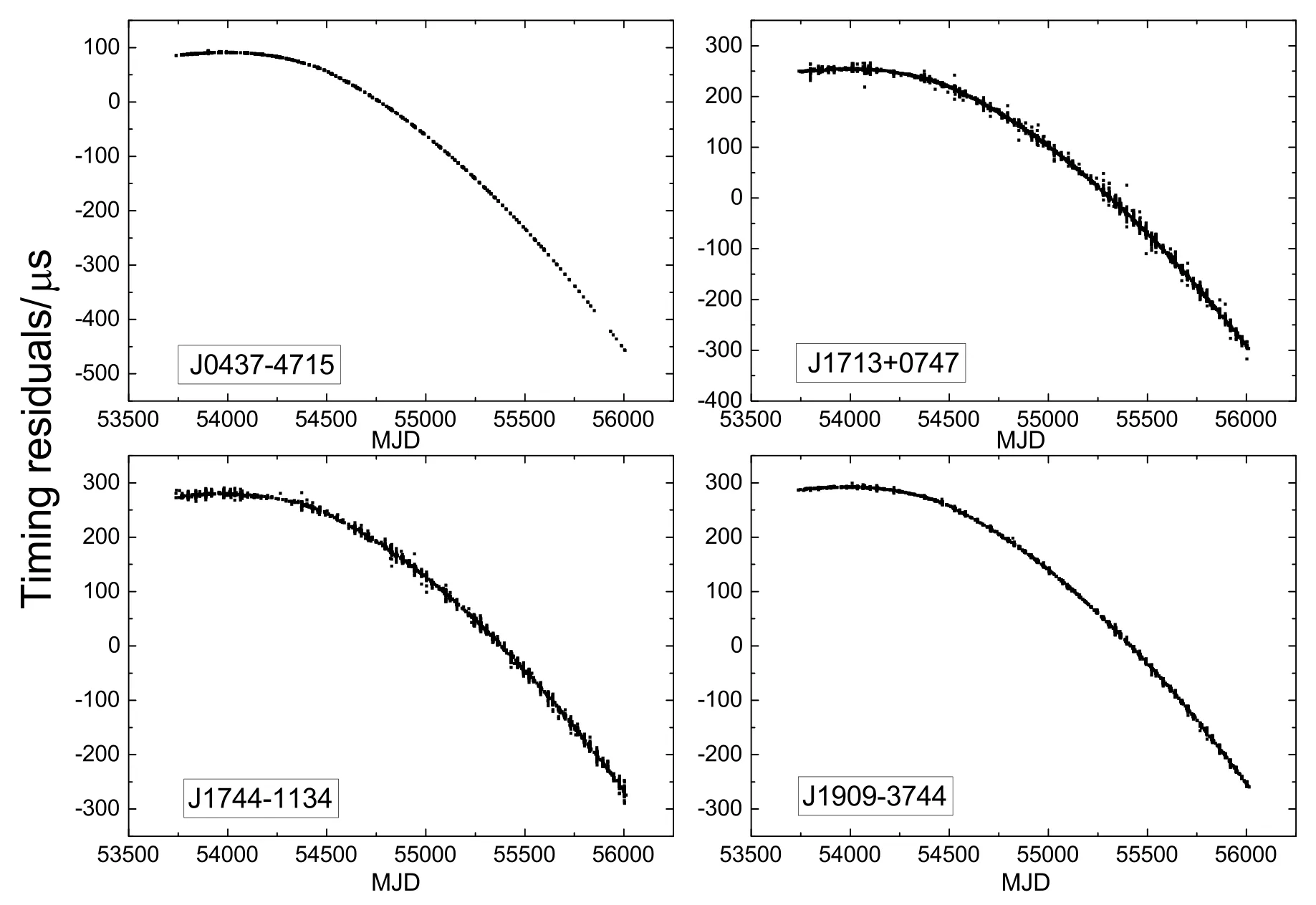
图5 参考钟为TT (H1404926)时四颗星的拟合前计时残差图Fig.5The pre-fit timing residuals of four pulsars when the reference clock is TT (H1404926)

3.2.1 单星抗差估计结果

将脉冲星时作为参考时标, 通过估计原子钟相对于脉冲星时的频率, 对原子钟的频率进行驾驭,最终将得到一个稳定性更高的时间尺度. 对于以氢钟作为记录脉冲到达时刻的参考钟时得到的拟合前计时残差, 利用抗差估计[24]每三个月为一个计算周期按(4)式迭代估计参考钟的频偏与频漂,直至结果趋于稳定. 在采用加权平均算法计算原子时的过程中, 原子钟的频偏与频漂估计一般采用最小二乘算法. 但最小二乘算法受粗差影响较大, 若测量数据中混入少量粗差, 则会导致估计结果与真值的偏离程度较大. 抗差估计是在观测值超过正常范围时, 限制观测值对平差的影响. 采用抗差估计可以在一定程度上减小脉冲星本身的计时噪声对估计结果的影响,提高频率偏差与频率漂移的估计精度.抗差估计的权因子函数应用较广泛的有IGG3函数与Huber函数[25], IGG3函数为:

Huber函数为:

式中,j为每个TOA的序号,wj为权因子,vj为观测值与拟合值之差, 即残差. 若以正态分布统计量构造权函数, 则在特定的显著性水平下权函数的界值可以固定. 为尽可能地减小脉冲星噪声对结果的影响并保留原子钟本身的特性, 根据拟合后残差vj的区间范围选取合适的界值. 对于J1744-1134脉冲星, IGG3函数的误差控制界值c1、c2分别选为10-8与10-5, Huber函数的界值c为10-8; 对于其他三颗星, IGG3函数的界值c1、c2分别设置为5×10-8与10-6, Huber函数的界值c设为5×10-8.

抗差估计得到的频率偏差与频率漂移结果如图6与图7所示, 其中图6使用的权因子函数为IGG3函数,图7使用的权因子函数为Huber函数.从图6与图7的对比结果来看, 二者对应的频率偏差与频率漂移的趋势基本一致, 说明两种权因子函数都可以有效抑制脉冲星噪声对估计结果的影响. 为方便起见, 下文我们只讨论使用IGG3函数的结果. 从四颗星的估计结果来看, J1744-1134与其他三颗星的估计结果偏离程度较大. 这是因为该星的计时精度相较于其他三颗星较低. 因此, 在脉冲星驾驭原子钟的应用过程中, 应选择计时精度高且不受红噪声影响的毫秒脉冲星.

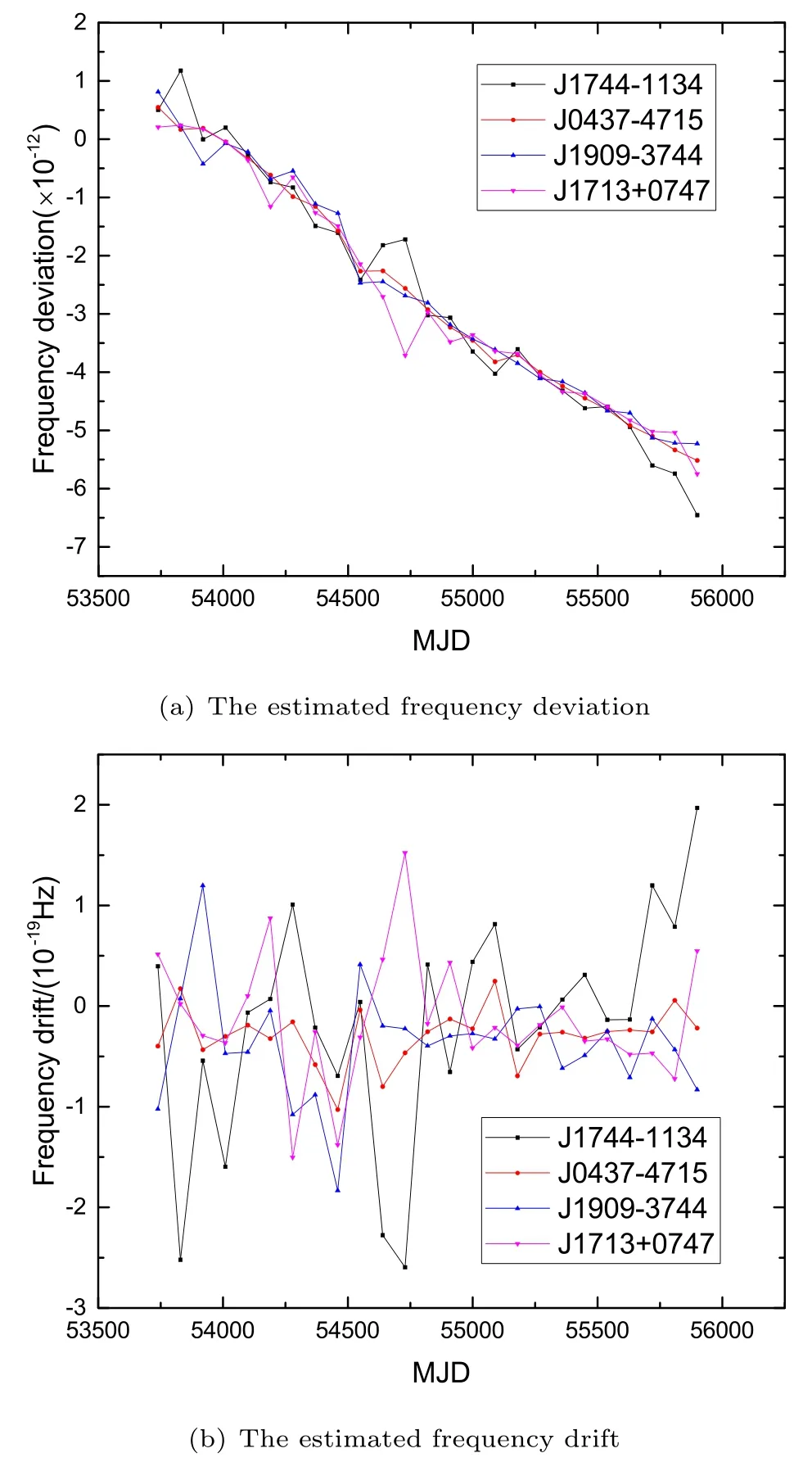
图6 四颗脉冲星数据抗差估计得到的氢钟H1404926的频率偏差与频率漂移. 权因子函数采用IGG3函数.Fig.6 The frequency deviation and frequency drift of the hydrogen maser H1404926 obtained by robust estimation using data of the four pulsars. The weight factor function is IGG3 function.

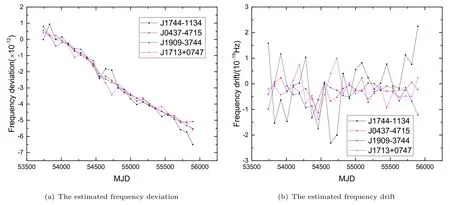
图7 四颗脉冲星数据抗差估计得到的氢钟频率偏差与频率漂移. 权因子函数采用Huber函数.Fig.7 The frequency deviation and frequency drift of the hydrogen maser obtained by robust estimation using data of the four pulsars. The weight factor function is taken to be the Huber function.

3.2.2 四颗星加权平均结果

为了有效降低单颗星的噪声对估计结果的影响, 下面对四颗星的拟合结果进行加权平均处理,每颗星的权重反比于各星以TT (BIPM)为参考时得到的拟合后计时残差均方根值RMS (Root Mean Square)的平方. 进行总权重归一化处理后, 得到四颗星(J0437-4715、 J1713+0747、 J1744-1134、J1909-3744)的权重Wj分别为0.228、0.290、0.025、0.457, 结果如表1所示. 四颗星综合处理的结果如图8所示. 同时, 图8还给出了每季度利用UTC估计的氢钟H1404926频偏与频漂值以及TT (BIPM)对应的估计结果. 通过与TT (BIPM)- TT(H1404926)得到的拟合结果对比可知, UTC对氢钟的频偏与频漂估计结果与TT (BIPM)估计的结果基本一致. 而经四颗脉冲星观测数据估计的氢钟频偏与氢钟相对于TT (BIPM)的频偏在前期差别较大, 后期符合程度较好, 这主要与脉冲星观测设备灵敏度的提升有关. 脉冲星时估计的氢钟频率漂移在TT (BIPM)对应估计值附近波动, 波动程度前期较大而后期较小, 波动量与脉冲星自身噪声、观测设备噪声、传播路径导致的噪声以及脉冲星计时模型精度有关. 为了与每季度驾驭结果进行比较, 图9与图10分别给出了每半年与一年利用TT(BIPM)、PT及UTC对氢钟H1404926的频率偏差、频率漂移的估计结果. 从估计结果来看, 驾驭周期越长, 脉冲星时的驾驭结果与TT (BIPM)的驾驭结果越接近. 为了更好地比较估计结果, 我们将驾驭周期为一年时三者的估计结果展示在表2中, 表中第一列为每个驾驭周期的起始时间, ^B、^C分别代表频率偏差与频率漂移的估计值. 从表2中的结果可以看出, 三者的频率偏差估计结果相近. 在后期研究中, 我们将筛选计时噪声小的多颗毫秒脉冲星进行综合处理, 并采用其他方法更好地扣除脉冲星自身因素对估计结果的影响.

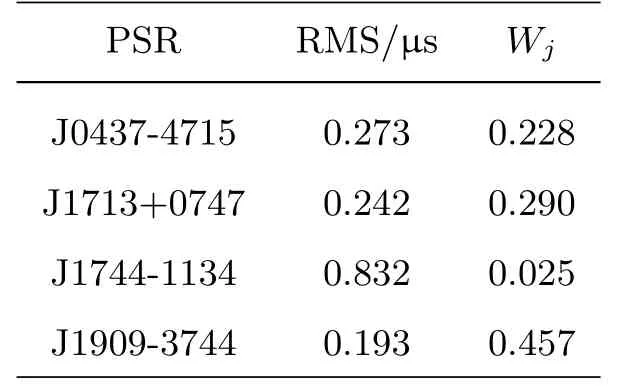
表1 四颗脉冲星的归一化权重Table 1 The normalized weights of the four pulsars

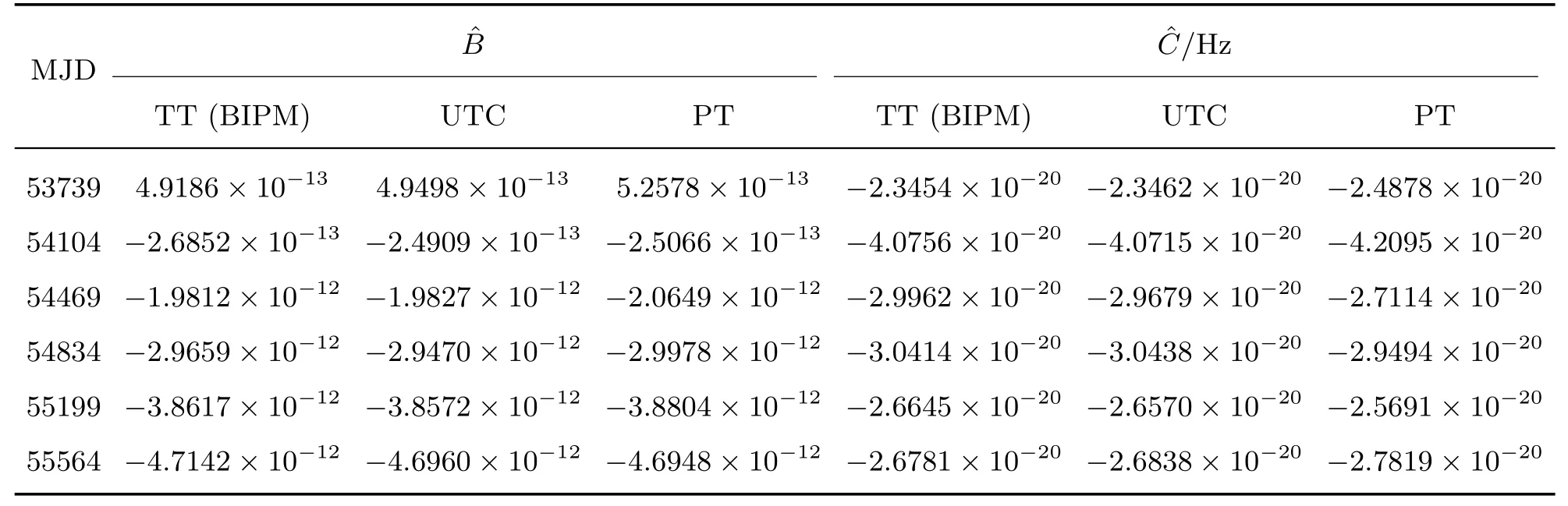
表2 驾驭周期为一年时频率偏差与频率漂移的估计结果Table 2 The estimation of frequency deviation and drift when steering cycle is one year

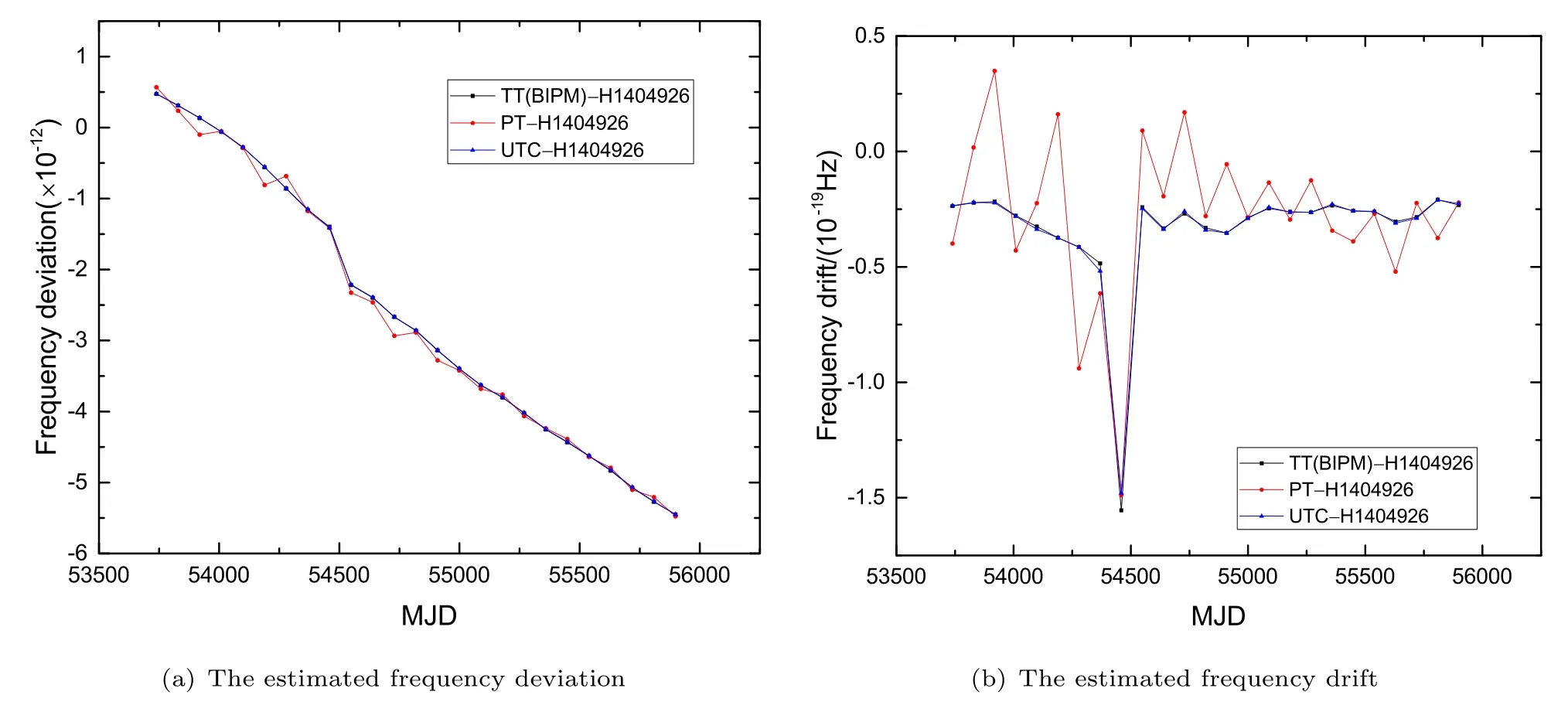
图8 四颗脉冲星估计结果综合处理得到的氢钟频率偏差与频率漂移. 图中的黑色数据点为由TT (BIPM)-H1404926每三个月进行二次三项式拟合得到的拟合值, 蓝色数据点为UTC-H1404926每三个月的估计结果, 红色数据点为四颗脉冲星加权平均得到的估计值.Fig.8 The frequency deviation and frequency drift of the hydrogen maser obtained by comprehensively processing the estimation results of the four pulsars. The black data points in the figure are the values obtained by the quadratic trinomial fitting of TT (BIPM)-H1404926 every three months, the blue data points are the estimated results of UTC-H1404926 every three months, and the red data points are the estimates obtained by the weighted average of the results of the four pulsars.

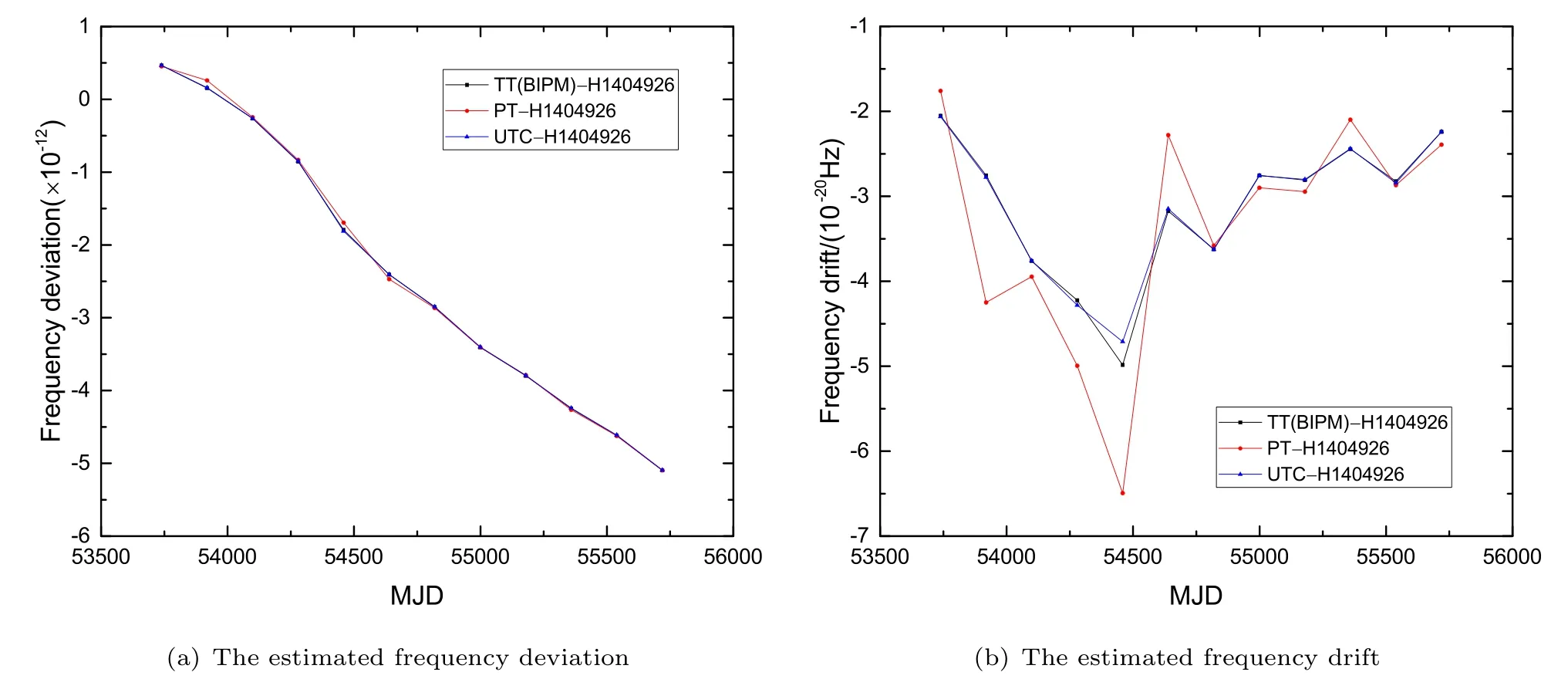
图9 四颗脉冲星估计结果综合处理得到的氢钟频率偏差与频率漂移, 驾驭周期为半年.Fig.9 The frequency deviation and drift of the hydrogen maser obtained by comprehensively processing the estimation results of the four pulsars. The steering cycle is half a year.

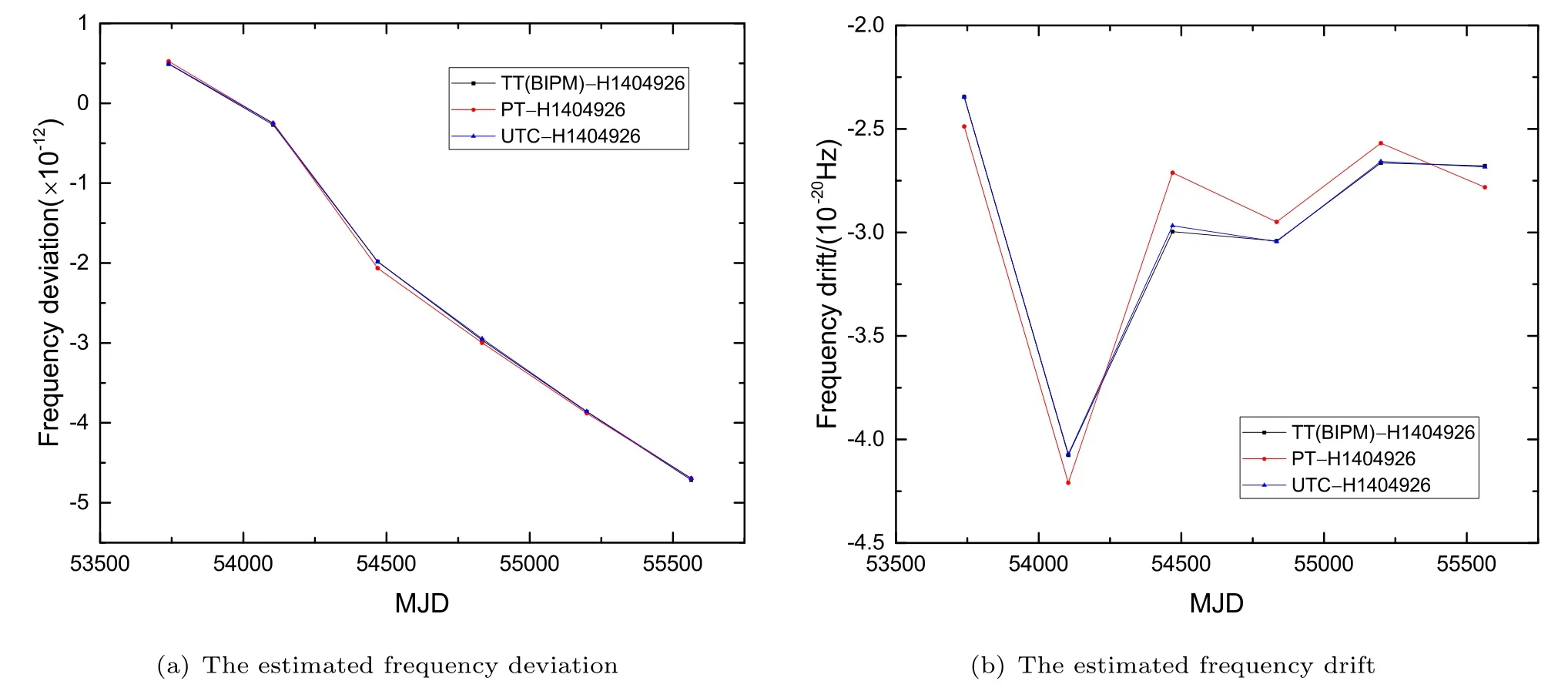
图10 四颗脉冲星估计结果综合处理得到的氢钟频率偏差与频率漂移, 驾驭周期为一年.Fig.10 The frequency deviation and drift of the hydrogen maser obtained by comprehensively processing the estimation results of the four pulsars. The steering cycle is one year.

根据上述氢原子钟频率驾驭流程, 可编制相应的软件, 将利用脉冲星时估计的频率偏差与频率漂移量作为频率补偿值加载到相位微调仪上, 实现对主钟频率的定期驾驭,从而提高本地时间的准确度.

4 总结与展望

本文利用脉冲星长期稳定度高的特性, 给出了脉冲星时驾驭单台氢钟的方法. 利用IPTA第二批发布数据中的四颗脉冲星数据, 根据文中方法得到氢钟的频率偏差与频率漂移. 此外, 采用加权平均算法分别得到了以每季度、半年、一年为周期脉冲星对氢钟的综合驾驭结果, 并与TT (BIPM)的驾驭结果进行对比. 由于脉冲星后期数据TOA测量精度高于前期, 二者的频率偏差估计结果在所用数据段的后期基本一致, 说明脉冲星源的选择、脉冲星的观测精度以及数据处理方法等均会对驾驭结果产生影响. 此外, 对不同驾驭周期的结果进行对比发现, 驾驭周期越长PT与TT (BIPM)的驾驭结果接近程度越高, 说明脉冲星的优势主要体现在其长期稳定度. 本文结果证实脉冲星驾驭氢钟具有可行性. 该方法可以在一定程度上弥补TT (BIPM)发布周期长的不足, 有望提高本地时间UTC (k)的准确性, 并对后期的相关研究具有一定的参考价值.

脉冲星TOA的测量精度及脉冲星钟模型参数精度是影响脉冲星驾驭原子钟精度的重要因素. 为提高脉冲星时驾驭原子钟的水平, 需将计时精度较高的毫秒脉冲星作为候选源, 同时提高观测设备的性能, 以提高TOA的测量精度. 此外, 需对候选脉冲星开展密集而持续的观测, 以缩短TOA的采样间隔, 并实现在时间上对原子钟的持续驾驭. 后续工作中, 脉冲星筛选、候选星取权方法以及将脉冲星时与原子时融合构建综合时间尺度的算法也是值得研究的课题.