大底板混凝土跳仓施工数字化监测与分析

张志敏，徐大为，潘 峰

（上海建工五建集团有限公司，上海 200063）

0 引言

混凝土作为一种脆性复合材料，其抗拉强度几乎只有抗压强度的十分之一左右。基于其组成材料的多样性，混凝土内部情况极为复杂，且容易受到外部各种条件的影响产生裂缝。贯穿性裂缝会直接破坏混凝土结构的稳定性和整体性，表面裂缝、深层裂缝随着拉应力的增大将进一步发展为贯穿裂缝［1］。根据资料显示在混凝土结构中 20 % 的裂缝源于外荷载，80 % 的裂缝却是由于温度、收缩变形等引起的［2］，因此如何控制混凝土浇筑及冷却过程中的温度是中外学者们一直以来都在探究的一个问题。

建筑大底板作为一种典型的大体积混凝土结构，最典型的特征便是其庞大的浇筑面积。由于混凝土散热性较差，大体积混凝土浇筑时内部水化热难以及时散发，而表面与空气对流温度下降较快，导致内外温差大，产生较大的温度应力。基于混凝土本身特性，其强度随着时间发展而增强，早期弹性模量较小，在温度应力影响下容易产生而温度裂缝。

为减小大体积混凝土中的温度应力，除了可通过改变混凝土组成成分降低水化生热量外，在施工技术方面，降低混凝土入模温度、设置冷却管、分层分块浇筑等方法都能有效减小温度应力。其中分层浇筑一般应用于大坝等超厚混凝土，在建筑大底板中分块跳仓浇筑的跳仓法［3］施工技术应用较为广泛，并逐步取代了传统的后浇带施工法。

1 工程概况

本工程为某大型室内滑雪场及其周边配套设施，总建筑面积 299 496.8 m2。基坑总面积约 87 638 m2，由于基坑面积较大，单边延长米较长，故本工程采用分区开挖的顺作法施工方式，将基坑由北向南一次划分为 A1 区、A2 区、B 区（见图1）。本工程地下室普遍区域面底板标高-7.8 m，板厚 650 mm，垫层厚100 mm。底板混凝土强度等级为 C40，抗渗等级为 P 6。

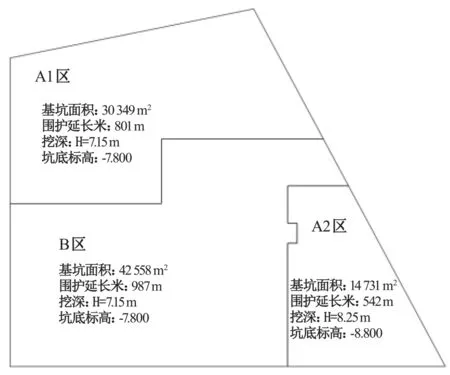
图1 顺作法底板分区

该工程底板面积较大，计划采用跳仓法施工，依据混凝土“抗”“放”原理，将 A 区大底板混凝土板分割成 20 个小仓块，每个仓块面积均不大于 1 600 m2（见图2）。

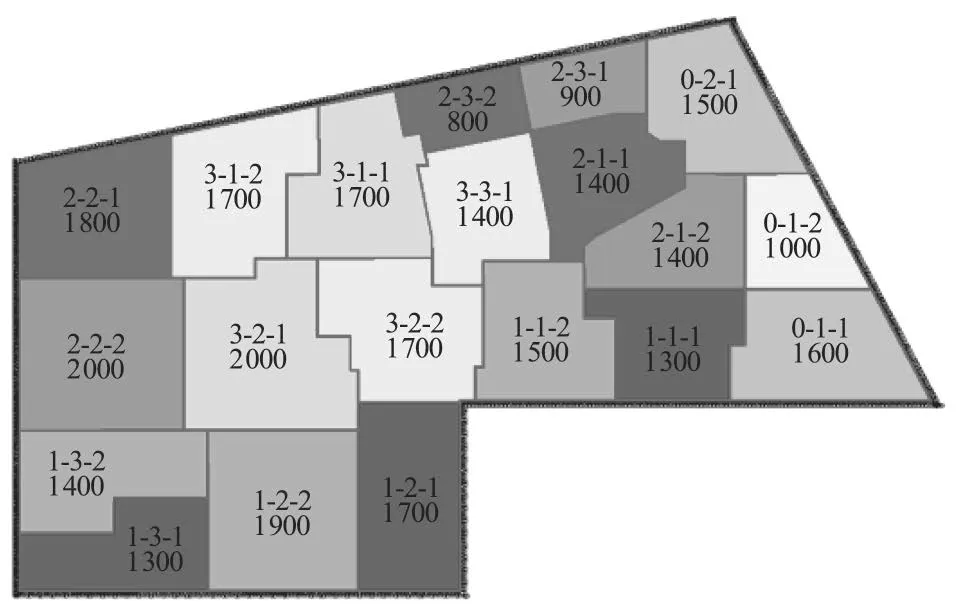
图2 A1 区底板分仓

进行混凝土浇筑时按照既定施工顺序间隔浇筑混凝土仓块，相邻混凝土仓块浇筑时间间隔为 7 d，期间穿插进行养护措施。

2 底板监测

为实测跳仓浇筑下混凝土底板的温度、应力和应变随龄期发展历程，本工程采用混凝土埋入式振弦式应变计对其进行监测。该仪器为一种利用振弦来进行测量的应变传感器（见图3），其结构简单，工作可靠，输出信号为标准的频率信号，后期计算机处理方便［4］。振弦式应变计原理为，当外部应力变化时会改变应变计内部钢弦频率，导致钢弦张力产生变化，通过测量钢弦频率的变化来计算外部应力。图4 为测点 9301 传感器温度变化后台显示曲线，该传感器设定为每小时测量一次。

图3 振弦式应变计安装示意装图

图4 实测温度变化曲线

3 仿真模拟

根据振弦式应变计埋设位置选取 A1 区域底板作为对象，同时选取了底板周围 5 m 内的土体加入模型进行有限元仿真模拟。为简化计算过程和计算时间，在进行仓块划分时进行了简化处理，但每一块仓块都控制在规定尺寸范围内，同时仓块浇筑采用两次浇筑方案。

有限元模型采用热单元 Solid 70，整个模型总计165 461 个节点，529 776 个单元，网格划分后模型图如图5 所示。网格划分完成后施加边界条件，包含土体边界绝热条件、混凝土与土体热量交换条件和混凝土与空气对流条件，再对混凝土施加生热率作为热源模拟其水化发热过程。其中模板及保温层对混凝土的保温效果换算为相应对流条件施加于混凝土模型表面，水化放热采用朱伯芳院士提出的双指数形式。采用“生死单元”程序［5］，即先“杀死”所有混凝土模型，再根据施工进度逐个进行激活并施加生热率，模拟先后两次浇筑仓块之间的热量传导，以达到模拟跳仓浇筑工况的效果。

图5 底板有限元模型

4 温度分析

4.1 温度曲线分析

实际首次浇筑日期为 2020 年 11 月 4 日，取测点9304 自 4 日 0 时起 20 d 的测温数据，该测点位于首次浇筑仓块中心的中间位置，此处混凝土温度变化最为剧烈。有限元软件中，在时间后处理中选取 18 号板块中心的中间节点温度进行分析，该节点与测点 9304 在空间上位置相近。将该节点 20 d 温度数据导出同实测数据一同绘制时间——温度曲线（见图6）。根据温度曲线选取了几个较为典型的时间节点的模拟温度云图以表现混凝土在浇筑过程中的温度分布（见图7）。

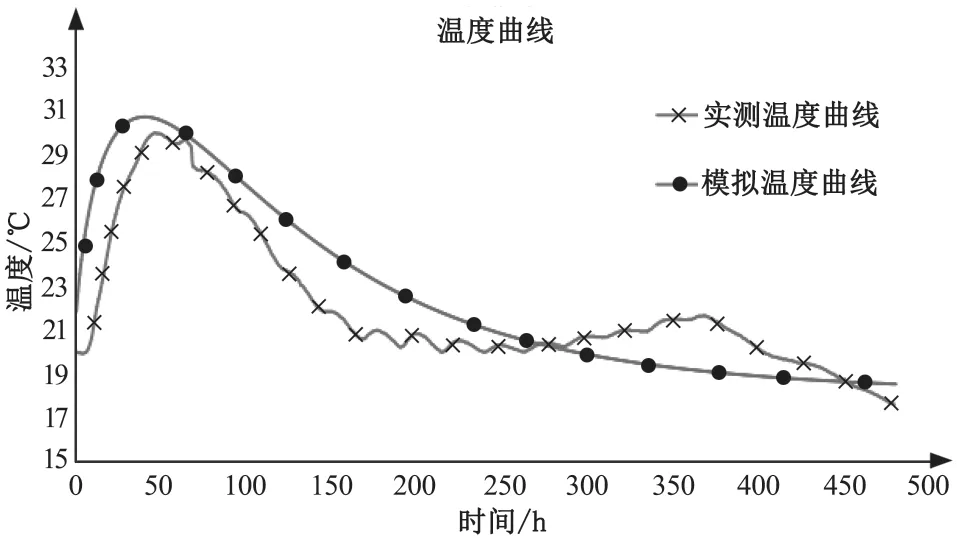
图6 实测与模拟温度变化对比

图7 模拟温度变化云图

从温度曲线对比图中可看出模拟结果与实测结果在温度变化趋势上基本一致。受混凝土水化热影响，二者内部温度均在 48 h 前后达到峰值。模拟数据中温度峰值为 30.533 ℃，实测数据中温度峰值为 29.56 ℃，二者的温度峰值基本一致。值得注意的是，从实测温度曲线反馈来看混凝土底板的实际冷却过程相较于有限元模拟数据曲线更为迅速一些。实测数据中显示混凝土内部在 150 h 左右降至环境温度趋于稳定，而模拟数据中此时间大致在 270 h 左右。且在降至室温后实测数据仍有不同程度的起伏。

图7 中分别截取了 10、40、240、250、280、480 h 的模型节点温度云图，从云图中可看出先浇仓块模型在 40 h 内迅速升温后开始降温，前期升温过程中仓块表面温度分布不均，至第 10 天 240 h 后浇仓块开始浇筑时，先浇仓块表面除靠近后浇仓块边缘部分受到后浇仓块混凝土水化热影响温度略有升高外，其余部分已经基本降至室温，且温度分布较为均匀。后浇仓块温度变化趋势和先浇仓块基本相同，二者温度峰值也基本一致，均为 31 ℃ 左右。

4.2 温度梯度分析

图8 为模拟温度梯度变化曲线，图9 为同温度云图时刻的混凝土仓块的温度梯度云图。从云图中可看出，前后浇筑的混凝土仓块均在 10 h 左右呈现最大内外温度梯度，均在 14 ℃ 左右，最大温度梯度出现位置基本为仓块的中心位置。结合先浇仓块 240 h 内的最大温度梯度变化曲线发现，10 h 内混凝土内外温度梯度迅速增大而此时混凝土温度尚未达到峰值。在后续 40 h 左右的时间段内混凝土仓块的温度梯度始终保持在 14 ℃左右，直到 50 h 后混凝土水化反应基本结束开始降温时温度梯度才开始下降。在 240 h 时，先浇仓块的内外温度梯度降低至 3 ℃ 左右，至 480 h 内外温度已经基本一致。

图8 模拟温度梯度变化曲线

图9 模拟温度梯度变化云图

5 应变计算

依据振弦式应变计测量理论，将应变计固定在测量物内部或者表面，钢丝弦和应变筒同步感受测量物变形，通过测量钢丝弦频率的变化反应测量物变形情况［6］。其变形计算公式如式（1）、（2）所示。

式中：ε为应变；E为钢丝弦弹性模量，GPa；f为应变计显示频率，Hz；f0为应变计初始频率，Hz；ρ为钢丝弦线密度，kg/m；L为钢丝弦长度，m。

上式为国内大部分振弦式应变计采用的计算模型，其K值一般由厂商经过计算标定。本工程选择的应变计同样采用上式进行应变计算。当测量对象的热膨胀系数与钢弦热膨胀系数存在较大差异时应当对应变进行温度修正。根据测点 9304 频率变化曲线（见图10）进行该点应变计算得到应变曲线（见图11）。

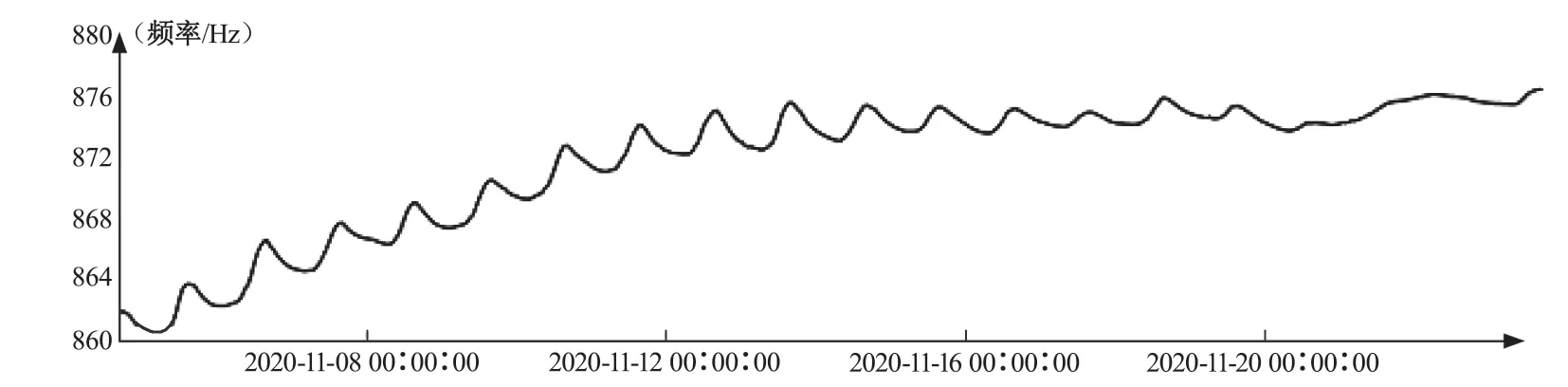
图10 9304 测点实测频率变化曲线

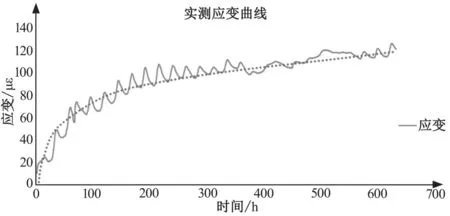
图11 应变曲线

其计算所得应变值包含了弹性变形、徐变变形、各部分收缩变形等［7］。通过应变计只能测量到该点的总应变值，无法具体呈现各种条件影响下的各个变形值。因此此处只考虑变形值的发展趋势及总变形值，并未具体深入各项变形值大小的计算。由于应变计在每天时间内频率呈现波浪起伏状（猜测为冬季施工时日温差较大导致），为较为直观表现应变发展趋势此处引入了应变曲线的拟合曲线（图11 中散点曲线）。经过几种函数拟合效果对比后，应变曲线与对数函数拟合最好，其拟合方程为：

ε=24.681ln（t）-39.777

从拟合曲线中可看出在 100 h 以前该测点应变值迅速增大，100 h 左右应变值为 80με左右。而在 600 h 后该点应变最大值为 120με，即在 100 h 到 600 h 的 500 h 内应变只增长了40με。通过对比温度变化曲线可看出在前 100 h 内为温度迅速增长与迅速降低阶段，此阶段温度变化剧烈；150 h 后温度变化缓和。因此可看出混凝土板块变形主要是受到前期猛烈的升温和降温过程影响，中后期温度缓和后的各项变形值增长较小。

6 应力分析

混凝土材料的性能在每个龄期都有不同情况的变化，且在各阶段都容易受到外界环境条件和施工方式的影响，导致了其应力表现在每个龄期也不同。在早龄期，即开始浇筑至水化放热反应基本结束这一阶段，此阶段的特点是水化反应导致内部温度急剧升高内外温差较大和弹性模量急剧变化。中龄期为混凝土冷却至接近室温的一个过程，晚龄期为冷却后的运行期。这两个阶段混凝土强度基本达标，其应力发展主要受到气温等外界环境因素的影响下与早期应力的叠加。

混凝土的弹性模量在前期剧烈变化，不同于完全弹性材料，混凝土的温度应力无法完全恢复，应力应变无法用简单的线性关系表达，因此本文采用增量法来计算混凝土内部弹性温度应力。

所谓增量法即将时间τ划分为一系列时间段Δτi（i=1，2，……），在此时间段内平均弹性模量为E（τi），温度增量为 ΔTi，则弹性温度应力增量［7］如式（3）所示。

考虑混凝土徐变松弛特性并引入徐变系数，应力累加后得到弹性温度应力公式为：

式中：σ（τi）为τi时段弹性温度应力，MPa；α为混凝土线性膨胀系数取 0.000 01；K（t，τi）为应力松弛系数取值见表1［8］。

表1 应力松弛系数取值

混凝土弹性模量表达式的取用在各个文献中略有差异，经过对几种常用表达式的对比分析本文采用以下指数式公式，该公式曲线能较好模拟混凝土实际弹性模量变化且考虑了混凝土掺合料的修正［9］如式（5）、（6）所示。

式中：E（t）为t时刻混凝土弹性模量，MPa；E0为混凝土养护 28 d 的弹性模量，本工程使用 C40 混凝土，E0取3.25×104MPa；φ系数取 0.09；β1为混凝土中粉煤灰对弹性模量的修正系数本工程取 0.99；β2为混凝土中矿渣灰对弹性模量的修正系数本工程中取1.02。

根据标准 GB 50496－2018《大体积混凝土施工标准》［10］引用混凝土抗裂性能作为判断混凝土安全性的依据，其判断公式如式（7）所示。

式中：σ为t时刻混凝土应力，MPa；ftk为t时刻混凝土抗拉强度标准值，MPa；K为防裂安全系数，取 1.15。

混凝土实时抗拉强度变化公式如式（8）所示。

其中：ftk为混凝土抗拉强度标准值，MPa，C40 混凝土抗拉强度标准值为 2.39 MPa；γ为系数，取 0.3。

根据弹性温度计算公式，取用上文测点 9304 实测数据与对应位置模拟数据计算其弹性温度应力，并将应力计算结果结合混凝土实时安全抗拉强度公式绘制应力变化曲线（见图12）。

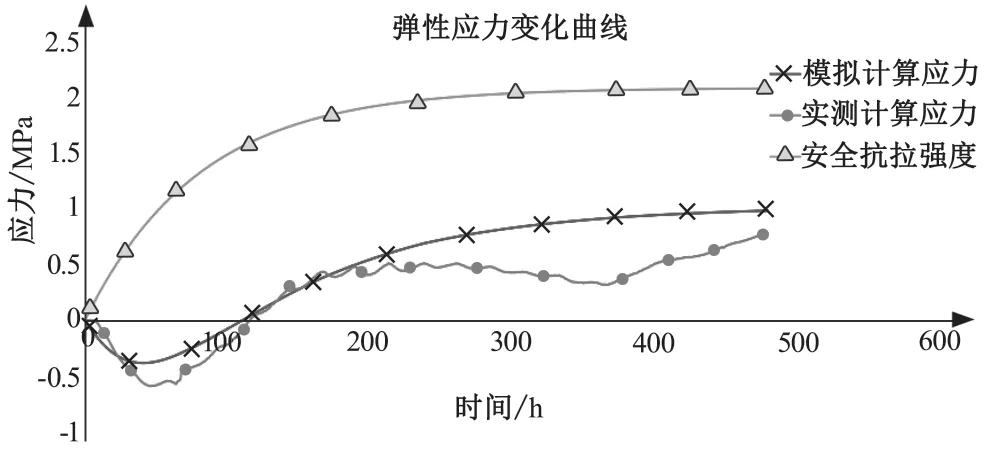
图12 弹性应力变化曲线

模拟数据计算的弹性应力最大值为 0.98 MPa，实测数据计算所得弹性应力为 0.78 MPa。从图12 弹性应力变化曲线可看出二者的曲线变化基本一致，在浇筑早期水化放热阶段混凝土升温，此时混凝土内部以压应力为主，在降温阶段拉应力逐渐增大，但由于弹性应力机制与早期产生的压应力叠加导致 100 h 以前混凝土内部还是呈现压应力状态。至 100 h 以后随着降温的进行，拉应力不断增大直到混凝土温度降低至趋近室温，此时混凝土内部拉应力不再发展。计算所得 C40 混凝土最大安全应力大概为 2 MPa，远大于实际和模拟计算的最大弹性温度应力，且安全应力在每时刻均大于弹性温度应力。从弹性温度应力理论来看，本工程大底板温度应力状态处于安全水平，且有较大的安全强度储备。

7 结语

1）根据模拟结果和实测结果的温度、应力数据曲线对比来看两者曲线变化趋势和峰值都较为接近。证明本工程数值模拟结果在一定程度能反应实际施工状态，可通过数值模拟结果对实际工程施工方案进行合理优化。

2）从温度测量和数值模拟结果来看，本工程最大升温为 31 ℃ 左右，内外最大温差为 14 ℃ 左右。根据相关规范规定大体积混凝土温控指标，混凝土在入模温度基础上升温不超过 50 ℃，内外温差不超过 25 ℃。从温度控制角度而言本工程温度远低于规定指标。

3）从应力与应变角度来看，根据应变计测量计算的最大应变值在 120 με，处于一个较小的应变水平。实测和模拟结果计算所得最大拉应力均在 1 MPa 左右，远小于本工程采用的 C40 混凝土的安全容许拉应力2 MPa。且从应力发展曲线来看结构应力始终保持在安全容许应力曲线之下，结构处于安全状态，且有较大的安全储备值。

4）实测数据频率曲线和温度曲线在一天范围内都存在较大的波动情况，考虑到本工程处于冬季施工状态，受日气温变化影响较大。即使数据显示结构较为安全但仍需考虑可能存在的极端天气对底板的影响，并做好相应的应对措施。Q