高超声速锥-柱-裙外形不同尾裙尺寸对轨控喷流干扰的影响

孙瑞斌,刘耀峰,张小亮,倪招勇

(中国航天空气动力技术研究院, 北京 100074)

0 引言

RCS(reaction control system)喷流是通过发动机喷流反作用力实现姿态和轨道变化的一种控制系统[1],已在多种飞行器中得到应用,基于用途的不同,RCS喷流大体可以分为2类:① 姿控喷流:提供俯仰、偏航及滚转力/力矩以保证或调整飞行姿态[2],例如:飞船返回舱(神舟、嫦娥)、航天飞机(X-37B)、滑翔飞行器;② 轨控喷流:在弹体质心附近提供直接力,以实现大过载、高机动变轨,例如:THAAD(theater high altitude area defense)[3]高速拦截弹、AIT(atmospheric interceptor technologies)[4]临近空间拦截弹等。

RCS喷流是姿/轨控发动机产生的燃气喷流,遇高速来流后形成复杂的干扰流场[5],干扰流场会改变飞行器外部气动环境,在喷口上游产生包含弓形激波、分离激波等的高压区,在喷口下游产生大范围的低压区,并由此产生附加干扰力、力矩;与姿控喷流相比,轨控喷流的流量、推力均高出一个量级左右,在相同的来流条件下,干扰范围明显增大,产生的干扰力、力矩影响更为显著;同时,喷流干扰效应与飞行高度、马赫数、飞行器布局等密切相关[6-7],在高空时(>40 km),来流密度低,流动通常为层流,产生的干扰力、力矩小,但分离点位置明显提前,更关注分离流场对弹体导引窗口的影响,在低空时,来流密度高,流动通常为湍流,产生的干扰力/力矩影响显著,对于飞行高度在20 km左右的拦截器,必须关注附加干扰力、力矩的影响。

对喷流干扰问题的研究始于20世纪50年代,其中对于弹类外形的研究内容包括:不同的头锥外形[8]、升力面外形影响[9-10]、喷口形状[8,11]等。进入90年代以后,进一步针对AIT拦截弹[6-7,12],THAAD[13]高速拦截弹等外形开展了大量的研究工作。研究的内容从基本流场结构[14]发展为对喷口布局[15-16]、冷/热喷差异[6-7,17-19]、喷流与舵面耦合干扰[20-21]、非定常效应[22-23]等多个方面的研究。随着高超声速拦截器的发展,对于轨控喷流的应用需求不断增强,也出现了少量专门针对轨控喷流的研究工作[24-25]。相关研究表明,喷口下游大范围的干扰流场内的压力变化是产生干扰力与力矩的主要原因,因此有必要开展喷口下游的飞行器几何特征对喷流干扰效应的影响研究基于使用轨控喷流控制的典型锥-柱-裙外形,开展M∞=5,H=20 km条件下的尾裙尺寸对喷流干扰效应的影响研究,重点关注尾裙底部直径与尾裙长度变化对气动力/力矩特性的影响。

1 研究对象及条件

锥-柱-裙外形由头锥、柱段与尾裙3部分组成(如图1),总长2 300 mm,弹体直径386 mm,如图1(a)所示,LT是尾裙长度,D是底部直径,θ是尾裙锥角。本文中研究用坐标系与弹体固连,原点为头部顶点,力矩参考点为喷流轴线与x轴交点,位于1 180 mm处,定义喷口侧弹体壁面子午线为0°子午线,喷流对侧弹体壁面子午线为180°子午线。计算网格采用分块对接结构网格,第一层壁面网格间距0.01 mm,半模计算网格量约420万,如图2所示。

图1 锥-柱-裙外形及坐标Fig.1 Cone-cylinder-flare configuration and coordinates

图2 计算网格Fig.2 Compute grid

在保证弹长不变的条件下,以为LT=367 mm,D=502 mm的尾裙外形为基准外形,改变尾裙底部直径、尾裙长度,对底部直径与尾裙长度的影响开展研究,具体外形尺寸如表1所示。

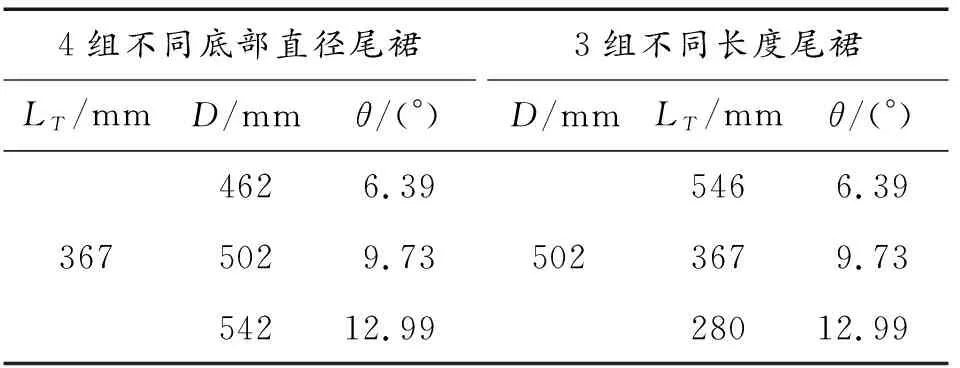
表1 尾裙尺寸

来流条件为M∞=5,H=20 km,α= -4～4°,喷流介质为常温空气,喷流出口压力133 310.9 Pa,总压2.87 MPa。

在姿控喷流干扰问题中,通常采用力/力矩干扰因子来表征喷流干扰对气动特性的影响。

(1)

式(1)中:Ki为喷流产生的附加干扰力/力矩干扰因子;ΔCi为附加干扰量;Ci, jeton、Ci, jetoff分别为有喷、无喷情况下气动力或力矩系数分量 (有喷力/力矩不含喷流本身产生的推力/推力矩);Ci, jet为喷流自身力/力矩系数,i代表y,Mz等分量,jetoff代表无喷,jeton代表有喷。

对于轨控喷流干扰问题,由于轨控发动机位于质心附近,喷流自身产生的力矩(Cmz, jet)为0或为小量,传统定义的力矩干扰因子失效,因此在本文研究中对法向干扰力采用传统的力干扰因子进行表征:

(2)

对俯仰干扰力矩定义轨控偏移量进行表征:

(3)

2 数值方法与验证

2.1 计算方法与模型

通过时间相关法求解三维RANS方程,对不同尾裙尺寸外形的干扰流场进行模拟。对流项离散选择能较好捕捉干扰流场中复杂的波系和涡系结构能力的二阶精度Roe格式,黏性项离散采用二阶精度中心差分格式,时间项离散使用LU-SGS隐式方法,采用局部时间步长加速收敛,湍流模型选择S-A湍流模型[26],S-A湍流模型是低雷诺数模型,第一层网格间距满足y+～O(1),当前第一层壁面网格间距0.01 mm,y+=0.2满足研究需求。

2.2 边界条件

1) 入流边界:来流为高超声速,入流边界处给定来流的静压、静温及马赫数。

2) 出流边界:出口为高超声速,将所有参数数值外推。

3) 物面边界:采用无滑移绝热壁面条件。

4) 对称面:对称面法向速度为零,对称面切向速度、密度、压力的对称面法向的梯度为零。

5) 喷流边界:喷管入口总压、总温及马赫数。

2.3 数值方法与验证

数值计算利用自编的适用于侧向喷流干扰效应研究的CFD软件[17],采用风洞试验结果对数值方法进行验证。试验条件为:P0=2 MPa,M∞=5,α=-4 ～ 4°,P0j=1.96 MPa,模拟20 km高度下的压力比,试验外形为本项研究基准外形的缩比外形(1∶6)。图3给出了常规高超风洞中完成的轨控喷流纹影图像。数值模拟得到的头激波、分离激波与弓形激波等流场结构与试验图像符合良好。

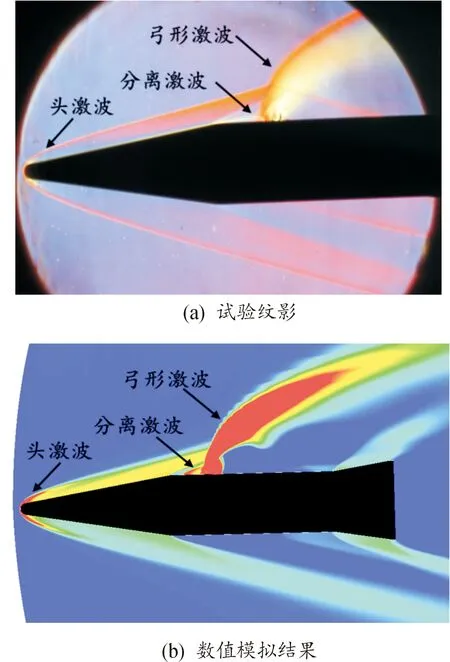
图3 流场结构对比Fig.3 Flow field structure comparison

图4给出了气动力/力矩结果的计算与试验对比情况。附加干扰力/力矩及力干扰因子的数值模拟结果与试验结果规律一致,精度良好。综上,数值模拟精度满足本项研究需求。

3 模拟结果与分析

锥-柱-裙类的高超声速飞行器在飞行过程中的攻角较小,且在喷流迎风时的干扰效应影响大,产生的附加干扰力矩大,是工程应用中重点关注的量。本文中对M∞=5,H=20 km,α=-2°条件下对轨控喷流干扰流场特征、尾裙底部直径的影响、尾裙长度的影响开展分析,最后给出了不同攻角条件下的尾裙尺寸变化对力干扰因子与轨控偏移量的影响规律。

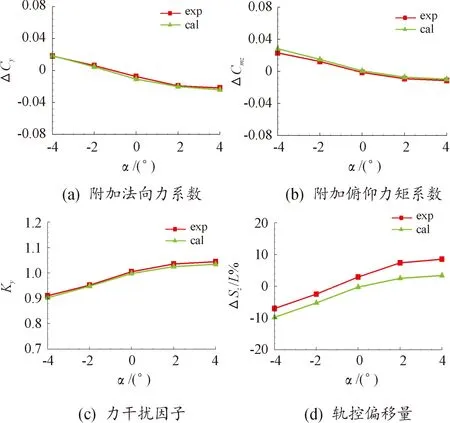
图4 气动系数的计算与试验对比(M∞=5)Fig.4 Calculation and test comparison of aerodynamic coefficient at M∞=5

3.1 锥-柱-裙外形轨控喷流干扰流场特征

图5给出了基准外形LT=366.95 mm,D=502.15 mm在M∞=5,H=20 km,α= -2°条件下喷流干扰流场图。如图5所示,喷流与来流干扰后产生弓形激波,分离与再附等流动结构,喷流上游存在高压区,喷流下游存在大范围的干扰流场,干扰流场会发展到喷流对侧的弹体表面,并导致大范围的弹体外部气动环境的改变。

图5 喷流干扰流场结构Fig.5 Flow field structure of jet interference

图6给出了0°与180°子午线的压力分布。如图所示在喷口侧(0°子午线),喷口上游产生弹体壁面压力升高,对喷流推力有增益效果;在喷口下游的柱段与尾裙段都产生了大范围的低压区,对喷流推力有减弱效果,同时,上述压力变化产生低头力矩。在喷流对侧(180°子午线)下游干扰区弹体壁面压力升高,对喷流推力有减弱效果,同时产生低头力矩。

图6 基准外形壁面压力分布 (LT=366.95 mm,D=502.15 mm)Fig.6 Pressure distribution on the baseline configuration wall (LT=366.95 mm, D=502.15 mm)

3.2 相同长度、不同底部直径尾裙的喷流干扰特性

完成了相同长度,不同底部直径尾裙外形的轨控喷流干扰流场数值计算,尾裙尺寸变化图7所示。

图7 相同长度、不同底部直径尾裙示意Fig.7 Flare of same length and different bottom diameters

图8给出了-2°攻角条件下,相同长度、不同底部直径尾裙外形的子午线压力分布。在尾裙处,尾裙底部直径对尾裙表面的压力影响明显,随着尾裙底部直径增大,有喷及无喷时的迎风侧(0°子午线)与背风侧(180°子午线)尾裙表面压力均升高。在迎风侧(0°子午线),有喷时的尾裙壁面压力低于无喷,该部分压差产生的干扰力对喷流推力有减弱效果,产生低头的干扰力矩,且随着底部直径增大,该部分的压差增加,附加干扰效应增强;在背风侧(180°子午线),整体而言,有喷时的尾裙壁面压力高于无喷,该部分压差对喷流推力有减弱效应,产生低头干扰力矩,但随着底部直径增大,该部分产生的压差减小,附加干扰效应减弱。

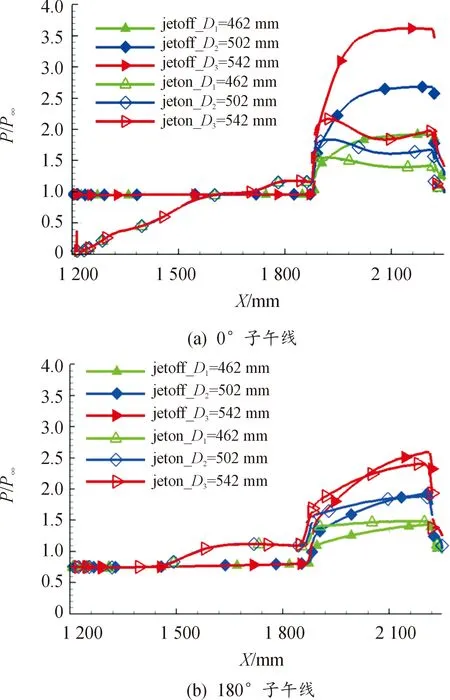
图8 相同长度、不同底部直径尾裙外形 子午线压力分布Fig.8 Meridian pressure distribution of tail flarewall with same length and different bottom diameters

图9给出了相同长度,不同底部直径尾裙外形的力干扰因子与轨控偏移量结果。

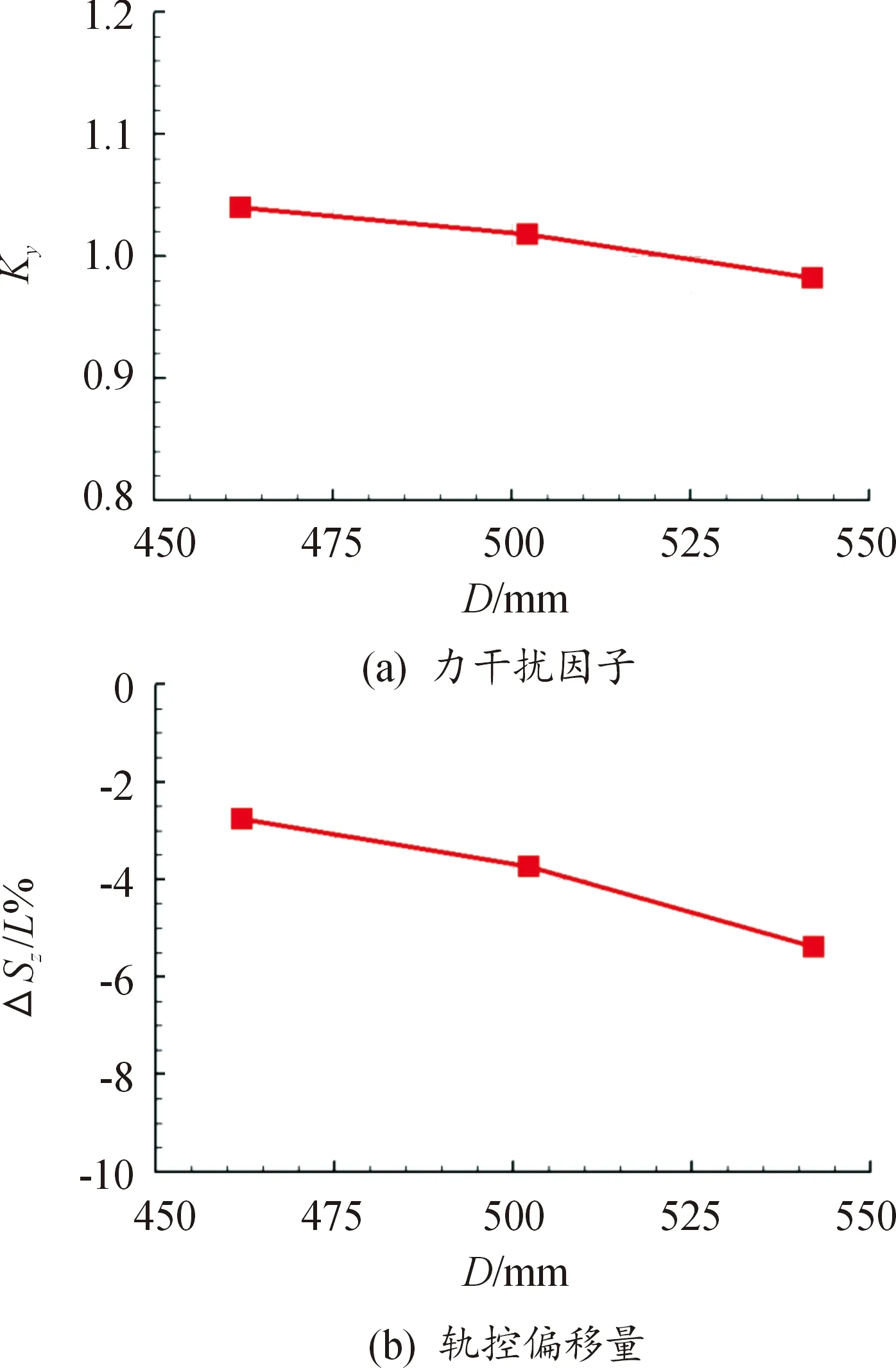
图9 不同底部直径尾裙外形力干扰因子 与轨控偏移量Fig.9 Force interference factor and shift of jet force center of flare with different bottom diameters

由图9可知,随着尾裙底部直径增加,力干扰因子减小,并由大于1向小于1转变,附加干扰对喷流推力由增益效果转变为减弱效果。轨控偏移量始终为负值,且随底部直径增加而量值增大,这表明附加干扰力矩始终为低头力矩,且随负攻角增大而增大。

3.3 相同长度、不同底部直径尾裙的喷流干扰特性

完成了相同底部直径、不同长度尾裙外形的轨控喷流干扰数值计算,尾裙尺寸变化如图10所示。

图10 相同底部直径、不同锥角尾裙示意图Fig.10 Flare of samebottom diameter and different lengths

图11给出了相同底部直径、不同长度尾裙外形的子午线压力分布。在迎风侧(0°子午线),有喷时的尾裙壁面压力低于无喷,该部分压差产生的干扰力对喷流推力有减弱效果,产生低头干扰力矩,随着尾裙长度增加,该部分压力变化区域范围增大,但压差减小。在背风侧(180°子午线),有喷时的尾裙壁面压力高于无喷,该部分压差产生的干扰力对喷流推力有减弱效果,产生低头干扰力矩,随着尾裙长度增加,该部分压力变化区域范围增加,但压差减小。

图11 相同底部直径、不同长度尾裙 子午线压力分布Fig.11 Meridian pressure distribution of tail flare wall with same bottom diameterand different lengths

图12给出了相同底部直径、不同长度尾裙外形的力干扰因子与轨控偏移量结果。

图12 不同长度尾裙外形的力干扰因子 与轨控偏移量Fig.12 Force interference factor and shift of jet force center of flare with different lengths

由图12可知,随着尾裙长度增加,力干扰因子变化较小,且始终大于1,附加干扰对喷流推力始终表现为增益效应。轨控偏移量始终为负值,且随着尾裙长度增加,轨控偏移量值变化较小。这是由于力干扰因子和轨控偏移量受到壁面压力积分值的影响,随着尾裙长度增加,尾裙壁面压差区域变大,但压差减小,因此导致的积分值变化不明显。

进一步对不同攻角条件下的尾裙底部直径与尾裙长度的影响开展研究,分析力干扰因子与轨控偏移量随攻角的变化规律。

图13给出了相同长度、不同底部直径尾裙外形的力干扰因子和轨控偏移量随攻角变化规律。由图13可知,尾裙底部直径在负攻角条件下产生的影响更大且规律一致。大的底部直径外形的力干扰因子小,轨控偏移量量值大且为负值,喷流作用点前移的距离大,产生更大的低头干扰力矩。结合图8的尾裙壁面压力分布可知,迎风侧的压力变化对附加干扰力/力矩的影响更大,且尾裙处的壁面压力变化随着负攻角增大而增大,并导致随负攻角增大,力干扰因子减小,轨控偏移量向负值增大。正攻角条件下不同外形的力干扰因子和轨控偏移量差别小,尾裙底部直径的影响较小。

图14给出了相同底部直径、不同长度的尾裙外形的干扰因子随攻角变化规律。

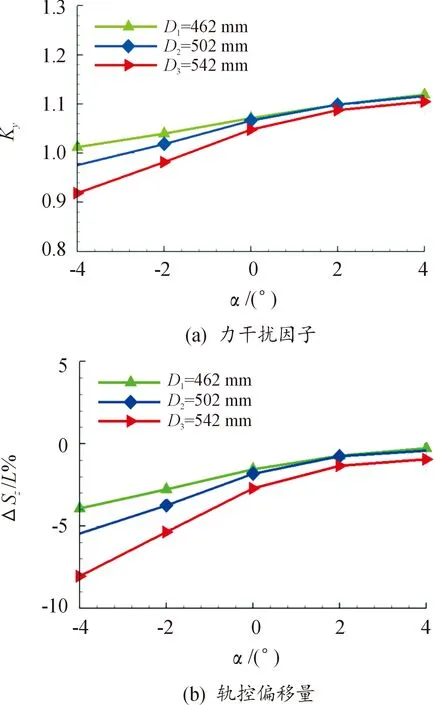
图13 不同底部直径尾裙外形力干扰因子 与轨控偏移量随攻角变化Fig.13 The force interference factor and shift of jet force center of flare with different bottom diameters vary with the angle of attack

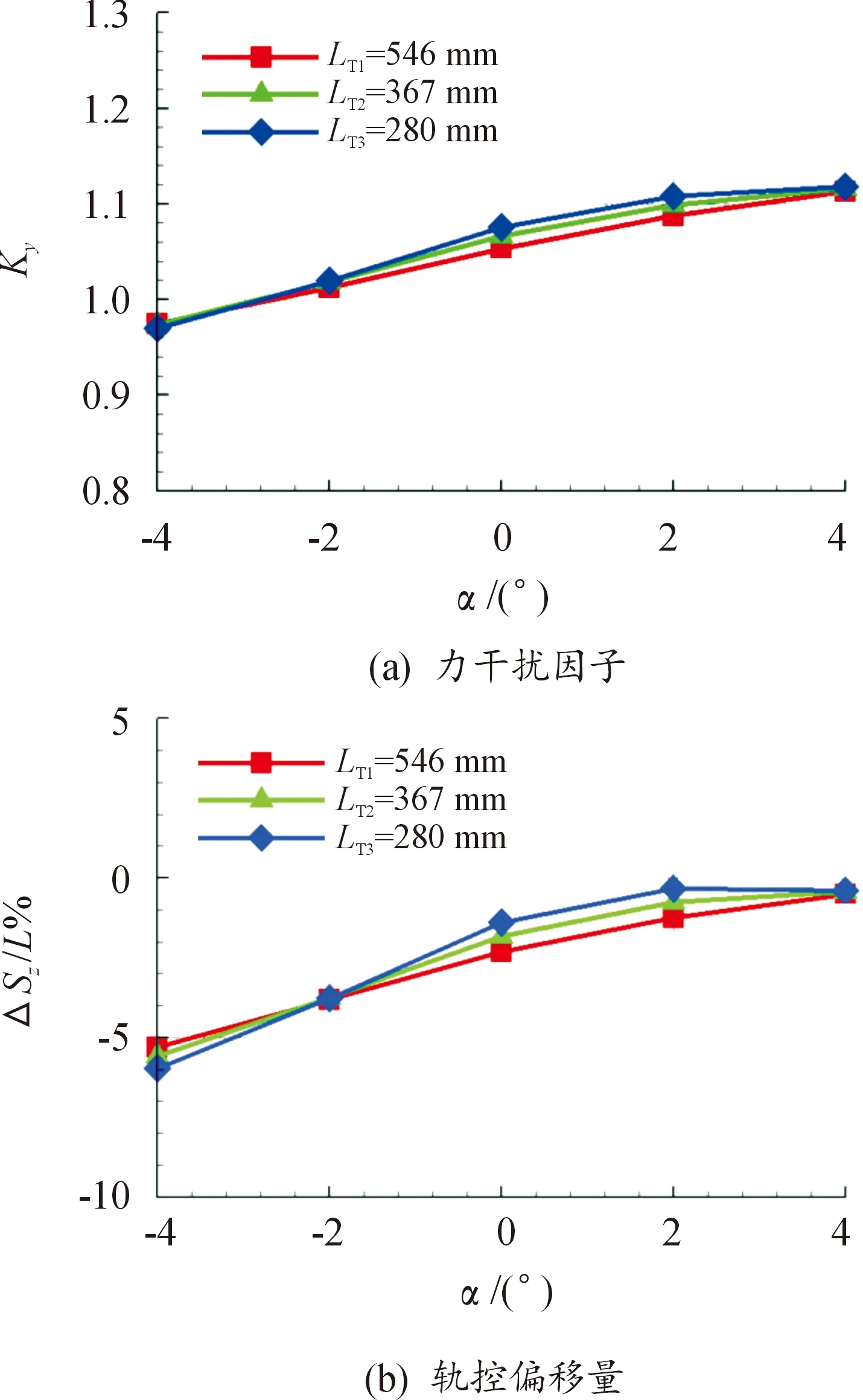
图14 不同长度尾裙外形力干扰因子和 轨控偏移量随攻角变化Fig.14 The force interference factor and shift of jet force center of flare with different lengths vary with the angle of attack

由图14可知,对于相同底部直径的尾裙外形,尾裙长度的变化的影响与攻角密切相关,在α=0°、2°条件下小的尾裙长度外形的力干扰因子大,轨控偏移量量值小,产生小的低头干扰力矩。在α=-2°、4°条件下尾裙长度对力干扰因子与轨控偏移量无明显影响;在α=-4°条件下小的尾裙长度外形轨控偏移量量值大,但力干扰因子差别小。

4 结论

针对不同尾裙尺寸的外形开展了轨控喷流干扰效应数值模拟研究,结果表明:

1) 尾裙几何参数尤其是尾裙底部直径对喷流附加干扰效应影响较大。

2) 对于相同尾裙长度外形,随着尾裙底部直径增加,力干扰因子明显减小,轨控偏移量量值增大。

3) 尾裙底部直径对力干扰因子与轨控偏移量的影响随着负攻角增加而增大,在正攻角条件下的影响较小。

4) 对于相同尾裙底部直径外形,尾裙长度对力干扰因子和轨控偏移量的影响受到攻角的影响较大,不同攻角条件下的规律不一致。