基于多孔介质LTNE模型刷式密封动力学特性研究

刘美红,张家豪,康宇驰

(昆明理工大学 机电工程学院, 昆明 650500)

0 引言

刷式密封是一种具有优良密封性能的接触式动密封技术,多应用于航空发动机的级间密封及轴承腔密封[1-3]。相较于迷宫密封,刷式密封具有质量较轻、磨损更低的优点,泄漏率仅是迷宫密封的1/10～1/5[4-6]。

气流激振是影响旋转机械系统稳定性的难点问题之一,气流激振是由密封径向间隙内气流对转子的切向气流激振引起的[7],因此封严气体的流场分布是由不同弯曲的流线组成的气流。然而,封严气体绕流刷丝束时不仅产生了漩涡流、同向流、射流及横向流等,还与刷丝束-转子接触区域摩擦产生的热量进行对流换热。因此,泄漏气体温度升高,引起体积膨胀加速[8-9]。刷丝温度和气流温度的不断上升会对刷式密封使用寿命和密封性能产生显著的影响,从而影响刷式密封动力特性。而刷式密封的动力特性直接影响旋转机械转子系统的稳定性[10]。因此,开展流体热膨胀情况下的刷式密封转子动力特性分析具有重要意义。

目前,大多学者基于多孔介质模型,采用CFD方法分析刷式密封压力分布,再计算得到刷式密封转子动力学系数。Wei等[11]将刷束处理成多孔介质局部热平衡模型(local temperature quilibrium,LTE)模型,研究单级刷式密封的转子动力特性,并给出转子动力特性系数随刷式密封几何参数的变化规律。Subramanian等[12]基于三维CFD方法及多孔介质LTE模型,求解了刷式密封转子动力特性,研究了离心和热增长对转子动力学特性的影响。结果表明,考虑热增长时,交叉耦合刚度和直接阻尼均表现突出。张元桥等[13]基于非线性达西多孔介质LTE模型,使用涡动转子法,建立了刷式密封转子动力特性的数学模型,研究刷式-迷宫密封的工况对其动力特性的影响。研究结果表明,进口预旋越大直接刚度越大,同时有效阻尼随越低,从而密封系统越不稳定。Wei等[14]采用非达西多孔介质LTE模型,研究不同间隙工况下刷式密封的转子动力系数,结果得出,当间隙增大时,直接刚度先急剧下降然后略有上升。交叉耦合刚度比较复杂,直接阻尼系数随间隙增大而增大,为转子增加了稳定系数。然而,目前的研究中都是基于多孔介质LTE模型建立刷式密封数学模型对刷式密封的动力系数特性进行研究,LTE模型忽略了刷丝与流体间的温度差,导致计算结果存在较大误差。

局部非热平衡(local temperature non-equilibrium,LTNE)模型在LTE模型基础上增加了刷丝与流体间的对流换热,弥补了刷丝与流体间温度差的问题。而基于LTNE模型建立刷式密封数学模型研究刷式密封转子动力特性较少。因此本研究采用LTNE模型建立刷式密封转子动力特性的数值预测模型,研究刷式密封转子动力特性系数,为刷式密封设计及转子动力特性系数的预测提供参考。

1 刷式密封多孔介质模型

1.1 刷式密封多孔介质LTNE模型控制方程

刷式密封中泄漏气体可视为理想可压缩气体,满足以下稳态的控制方程[15]。

连续方程:

div(ρεV)=0

(1)

动量方程:

ρ(V·▽)V=-▽p+μ▽2V+SV+Si

(2)

理想气体状态方程:

p=ρRT

(3)

式(1)—式(3)中:ρ为气体密度;ε为多孔介质孔隙率;V为速度矢量;p为气体压力;μ为流体粘度;SV为广义源项;Si为动量源项;R为气体常数;T为温度。

多孔介质模型采用经验公式定义多孔介质对流体的阻力,即在动量方程中增加一个动量消耗的源项,该源项由粘性阻力损失和惯性阻力损失组成。本文中采用多孔介质模型中的Ergun方程推导刷式密封多孔介质区域的粘性阻力系数和惯性阻力系数,将轴向、周向和径向粘性阻力系数分别定义为ax、ay和az,惯性阻力系数分别定义为bx、by和bz,使用经验公式如下[9]:

(4)

式(4)中:D为刷丝直径;孔隙率ε是指刷式密封中多孔介质区域的微小孔隙体积与整个多孔介质区域总体积的比值,是多孔介质模型最重要的参数之一。根据刷式密封的几何结构得出孔隙率随刷式密封刷丝径向尺寸的关系:

(5)

式(5)中:Vs、V分别为刷丝体积和多孔介质区域总体积;N为刷丝束密度;D为刷丝直径;Dr为转子直径;r为刷丝径向高度;ω为刷丝束轴向厚度;Φ为刷丝束倾斜角。

流体经过多孔介质区域时,流体域与固体域之间存在一定温差,两者间会进行对流换热,LTNE模型使用2个能量方程表征了两者间的对流换热过程,分别为[16]

(6)

式(6)中:α为界面面积密度,即流体与固体接触面积与多孔介质区域体积的比值;κsf为流体与固体表面对流换热系数。从式(6)中可以看出LTNE模型增加了对流换热项。

在使用LTNE模型时,需要确定刷丝与气流的表面传热系数。参考了文献[17]中外掠单管对流换热模型,根据谢努尔特准则可以确定对流换热系数。

(7)

式(7)中:κsf为对流换热系数;κf为流体的导热系数;D为刷丝直径;Re为参与对流换热流体流动的雷诺数;Pr为参与对流换热流体的普朗特数。雷诺数和普朗特数分别为

(8)

Pr=Cpfμκf

(9)

式(8)、式(9)中:v为流体最大流速;μ为动力粘度。

1.2 刷式密封物理模型

刷式密封的基本结构示意图如图1所示。刷式密封主要由前挡板、刷丝束以及后挡板组成[18],刷式密封的工作原理是刷丝与转子接触,阻止气流通过。主要目的是限制主流路气流的流动和损失,防止气流出现回流和泄漏,表1给出了刷式密封的具体几何尺寸。

图1 刷式密封结构示意图Fig.1 Schematic diagram of the brush seal structure

表1 刷式密封几何尺寸Table 1 Brush seal geometry

1.3 边界条件及几何参数

本文中使用ANASYS 19.2仿真软件进行数值计算,基于多孔介质LTNE模型采用RANS方程求解,并用后处理软件进行数据后处理,几何参数采用文献[19]。表2给出了计算边界条件及不同结构参数。

表2 边界条件

由于整体模型划分网格较多,计算比较复杂,如图2所示,选取了1/6圆弧对称结构的网格划分模型。采用有限元软件Mesh模块划分网格,网格数量500万,网格质量良好。图2给出了模拟刷式密封结构的计算区域图,包括流体入口区域,出口区域以及刷丝束区域,采用RNGk-ε湍流模型。根据所采用的RNGk-ε湍流模型对近壁区网格的要求,壁面第一层网格高度设置为0.15 mm,对应的y+<5。

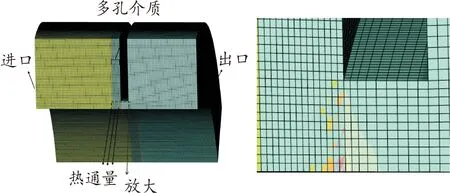
图2 数值模型网格划分Fig.2 Numerical model grid meshing

在刷式密封传热过程中,刷丝束与转子摩擦时产生的热量为[20]

Qh=Ffv=μFnv=μΔr·γBTPv

(10)

式(10)中:Ff为刷丝束与转子的摩擦力;v为刷丝束与转子的相对滑动速度;μ为摩擦因数,选取0.3[23];Fn为刷丝束与转轴的法向接触力;Δr为刷丝束与转轴干涉量;γBTP为刷丝束硬度,取值范围为54.3～1 085.8 MPa/m[23]。

2 刷式密封-转子系统动力特性

2.1 动力特性系数识别方法

刷式密封在运行时,转子发生旋转运动,当转子在静子中以小位移振动时,流体流动产生气动力,可简化为下列斜对称矩阵[24]:

(11)

动力学系数可通过以下公式得到:

Fr/e=-(K+cΩ)

(12)

Ft/e=k-CΩ

(13)

式(12)、式(13)中:e为转子偏心率;Ω为转子转速(r/min)。直接刚度系数K主要影响转子系统的最大临界速度,正向的直接刚度系数将增加转子系统的临界速度;交叉刚度系数k和直接阻尼系数C影响转子系统的稳定性,交叉刚度系数越大,转子系统稳定性越差,正向的直接阻尼系数可以抑制转子的不稳定性,而负的直接阻尼系数导致转子不稳定;而交叉阻尼系数c对转子系统无明显作用。

转子的偏心运动是动态的,为了避免网格的瞬态变化,在研究中建立一个将瞬态转为稳态的相对坐标系,图3(a)为绝对坐标下转子和静子的转速,图3(b)为相对坐标下转子和静子的转速,ω为网格的转速,ω-Ω为转子的相对速度,o′为转子偏心坐标原点,其中在相对坐标下,静子的转速为-Ω,如图3所示。

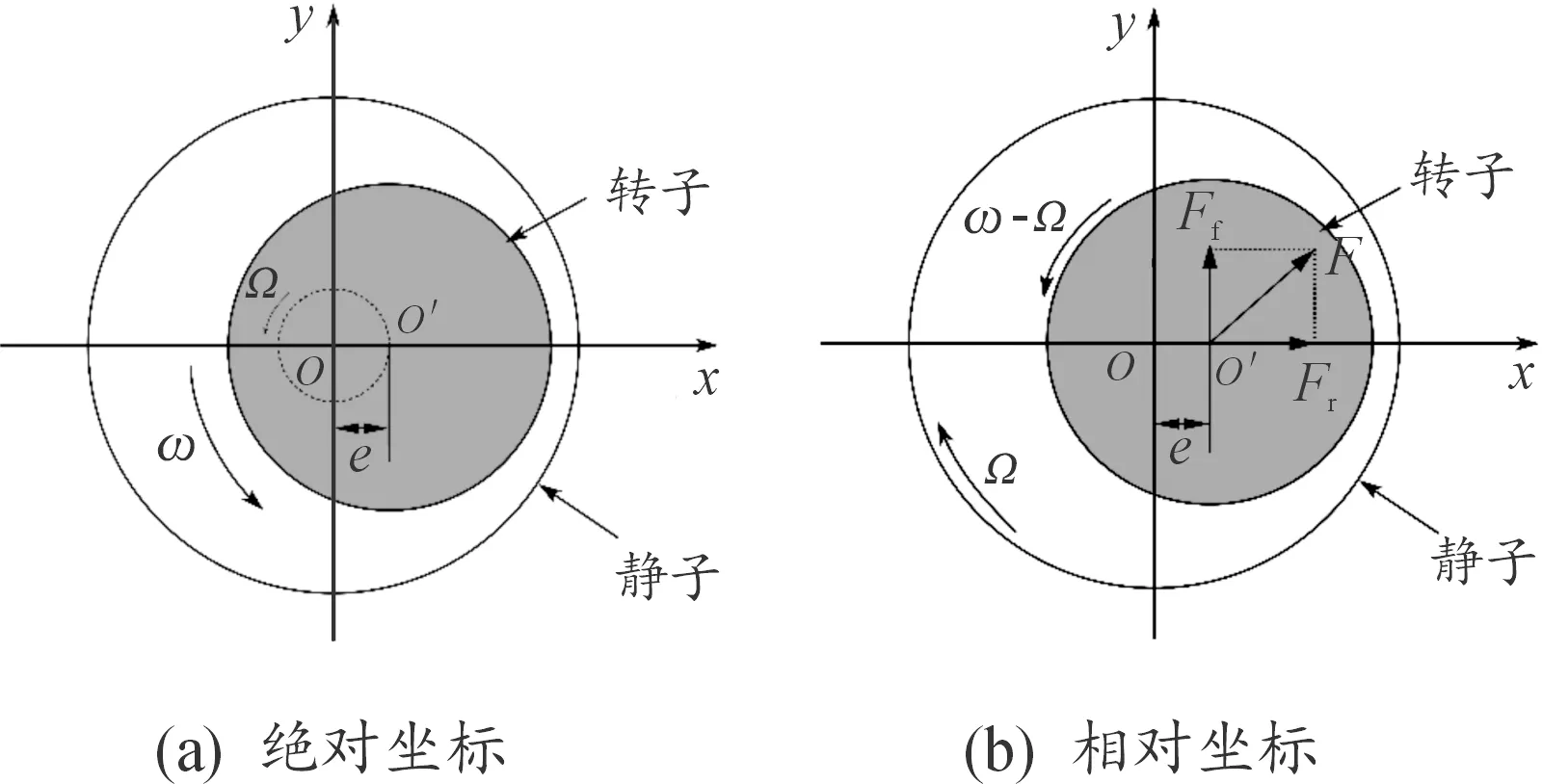
图3 坐标转换示意图Fig.3 The schematic diagram of coordinate transformations

式(12)中的径向力和切向力可以通过计算不同轴向位置圆周的静压力得到,如图4所示[11]:

图4 压力计算示意图Fig.4 The schematic diagram of pressure calculations

当φ=φ及α=β时,静压力为

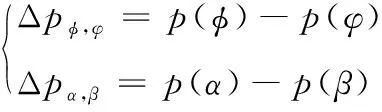
(14)

因此,径向力和切向力可以分别表示为

(15)

式(15)中: Δp、p为静压;φ、φ为径向力的角度;α、β为切向力的角度;x为轴向方向,L为轴向的密封长度。

2.2 动力特性系数求解

图5给出本文中刷式密封转子动力特性系数计算流程。首先基于CFD方法和多孔介质模型建立刷式密封动力特性数值计算模型;随后进行网格划分及边界条件设置,并加入热通量及对流换热的UDF输入,进行流固热耦合计算模型;最后由刷式密封周向压力求解径向力和切向力,进而求解转子动力特性系数。

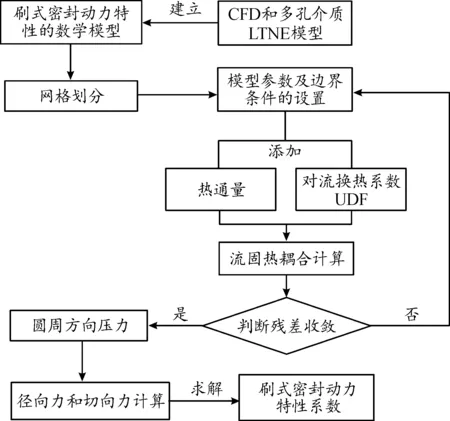
图5 动力特性系数计算流程框图Fig.5 The flow chart of dynamic characteristic coefficient calculationt

3 模型准确性验证

图6所示的是本文中计算的刚度系数与文献[13]中数值的对比。本文中数值计算的直接刚度系数K和交叉刚度系数k与文献中的数值随压比变化呈现相同的变化趋势,由于刷丝与转子接触时,刷丝弯曲程度不同导致数值计算存在误差,直接刚度系数K误差大小在18.6%～21.9%,但整体吻合良好。

图6 刚度系数计算值与文献[13]中数值对比Fig.6 Stiffness coefficient comparison between numerical values and Zhang’s

图7所示的是本文中计算泄漏率与文献[25]中的数值的对比。可以看出计算结果与文献中的数值吻合良好,有相同的增长趋势,由于考虑刷丝与转子间存在不同大小间隙,泄漏率数值上存在误差。

图7 泄漏率数值与文献[25]中数值对比Fig.7 Leakage rate comparison between numerical values and Gaszner’s

4 结果与分析

4.1 直接刚度系数K的影响因素

图8—图10分别给出了直接刚度系数K在不同压比下随刷束厚度、栅栏高度及间隙增加时的变化规律。由图8可见,随着刷束厚度增加,直接刚度系数K整体上呈现先减小后增加的趋势。而压比Rp等于5时,直接阻尼系数K随刷束厚度一直减小,但减小的较少。由于压比越高,刷丝束紧缚在一起与后挡板接触,刷丝束刚度增加,抵抗变形的能力增加,直接刚度系数K越大。

图8 刷束厚度对刷式密封直接刚度系数K的影响Fig.8 Effect of brush bundle thickness on the direct stiffness coefficient K of the brush seal

图9 栅栏高度对刷式密封直接刚度系数K的影响Fig.9 Effect of fence height on the direct stiffness factor K of the brush seal

图10 间隙对刷式密封直接刚度系数K的影响Fig.10 Effect of clearance on the direct stiffness factor K of the brush seal

由图9可知,直接刚度系数K整体上随栅栏高度增加呈现先增加后减小的趋势,压比越大,K值也越大,当栅栏高度为2.1 mm时,直接刚度系数K达到最大。当栅栏高度较小时,流体流经刷丝后通过后挡板,流速增加,直接刚度系数K增加;随着栅栏高度增加,流体经过刷丝束后会产生一个涡流,使流速减小,直接刚度系数K减小。由图10可知,直接刚度系数K随间隙增加呈现先减小后增大的趋势,在间隙等于0.1 mm之后,压比越小,K值增加的越多,在间隙大于0.2 mm时,压比越小,K值增加的越少。由于刷丝与转子间存在间隙,流体从间隙流过,刷丝变形减小,抵抗刷丝变形的能力减小,直接刚度系数K减小。但随着间隙的增加,流体经过刷丝束后会产生涡流,增加刷丝的变形,使直接刚度系数K增加。

4.2 交叉刚度系数k的影响因素

图11—图13所示分别为交叉刚度系数k在不同压比下随刷束厚度、栅栏高度及间隙增加时的变化规律。由图11可以看出交叉刚度系数k随刷束厚度增加呈现先增加后减小的趋势,并且压比越小数值越大。随刷束厚度的增加,经过刷束区域流速减小,交叉刚度系数k减小。由图12可以看出交叉刚度系数k随栅栏高度的增加先减小后增加。在栅栏高度小于2.1 mm时,压比越大交叉刚度系数k下降越多;栅栏高度大于2.1 mm时,压比越大交叉刚度系数k上升梯度越大,直到栅栏高度为2.5 mm时,压比越大交叉刚度系数k越大。这是由于栅栏高度增加,流速减小使交叉刚度系数减小,但栅栏高度高于2.1 mm时,随栅栏高度增加,产生涡流增加刷丝变形,从而增加交叉刚度系数k。由图13可以看出交叉刚度系数k整体上呈现先增加后减小的趋势,在间隙为0时,压比越大交叉刚度系数k数值越小,随着间隙的增加压比大的交叉刚度系数k数值也越来越大,直到间隙为0.2 mm时,压比越大交叉刚度系数k数值越大。当间隙继续增加到0.3 mm时,交叉刚度系数k减小,压比越大交叉刚度系数k降低的越多。直到间隙为0.3 mm时,压比大的交叉刚度系数k越小。随间隙增加,交叉刚度系数k变化与直接刚度系数K变化完全相反。

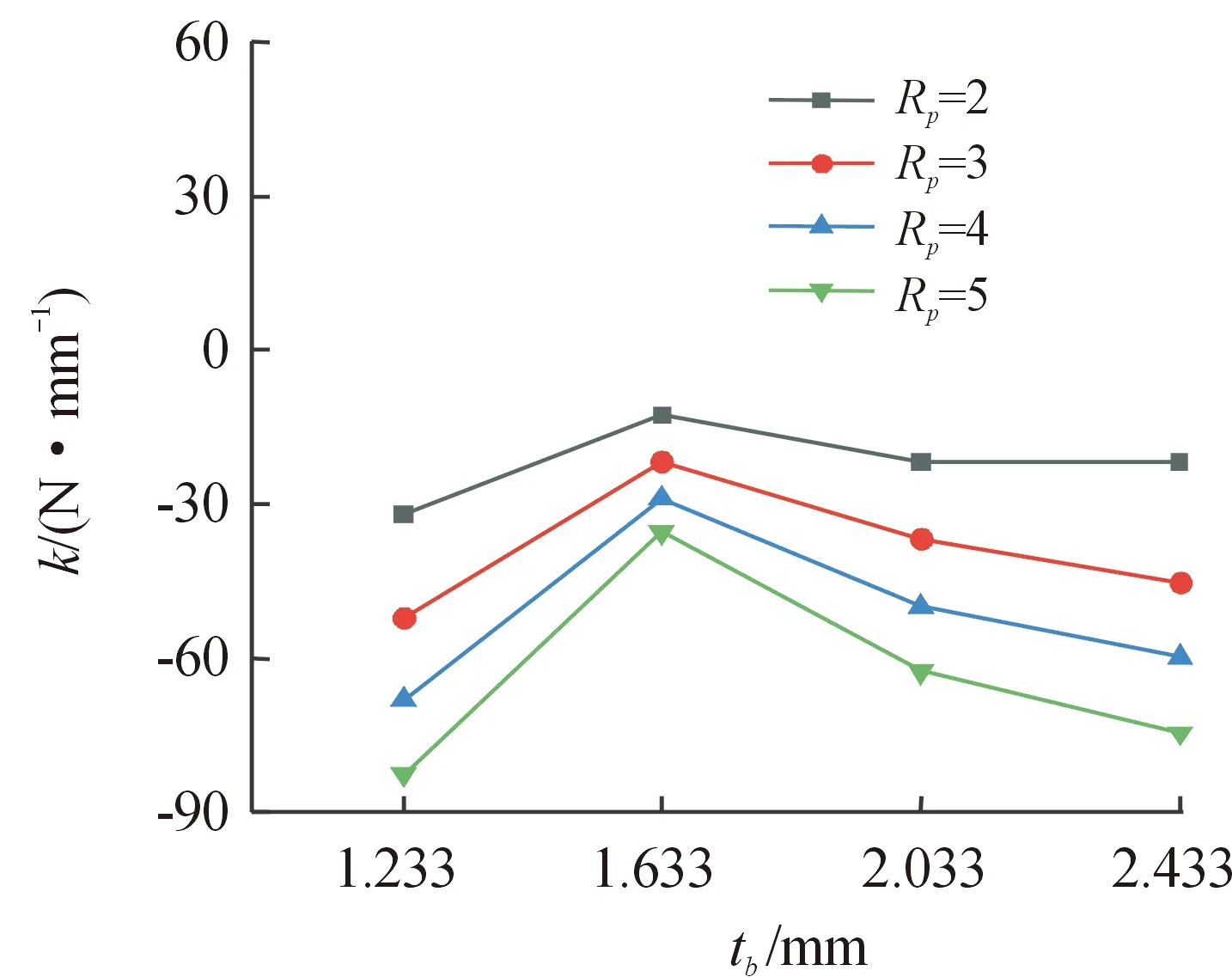
图11 刷束厚度对刷式密封交叉刚度系数k的影响Fig.11 Effect of brush bundle thickness on brush seal cross stiffness factor k

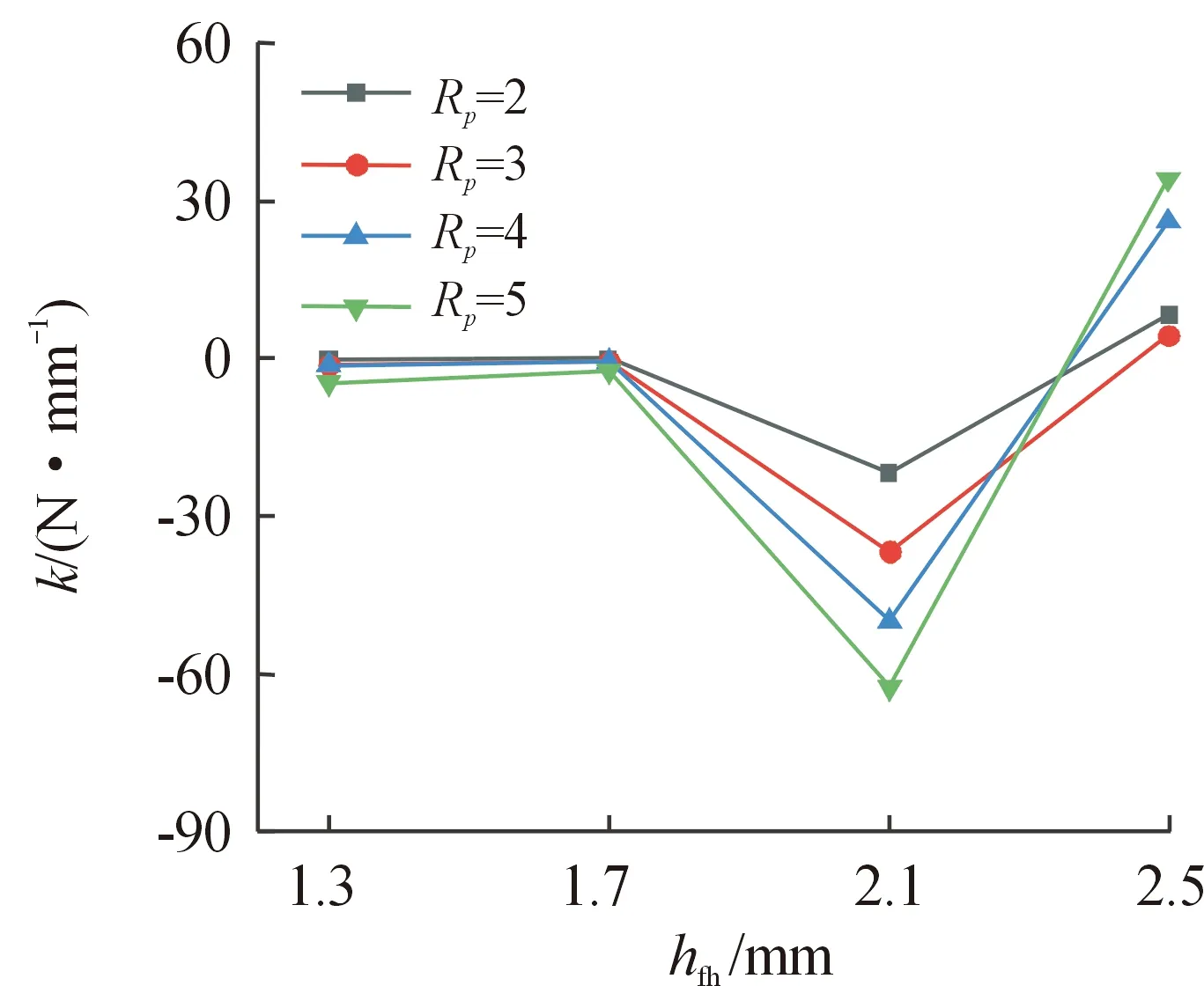
图12 栅栏高度对刷式密封交叉刚度系数k的影响Fig.12 Effect of fence height on brush seal cross stiffness factor k

图13 间隙对刷式密封交叉刚度系数k的影响Fig.13 Effect of clearance on brush seal cross stiffness factor k

4.3 直接阻尼系数C的影响因素

图14—图16分别给出了直接阻尼系数C在不同压比下随刷束厚度、栅栏高度及间隙增加时的变化规律。由图14可以看出不同压比下直接阻尼系数C在0值附近变化,有少量增加但不明显,可以看出直接阻尼对刷束厚度的变化并不敏感。由于刷束厚度增加,刷丝束对流体的阻碍作用增加,直接阻尼系数C增加。由图15可以看出压比为2和4时,直接阻尼系数C变化并不明显。压比为3时,直接阻尼系数C随栅栏高度的增加呈现先增加后减小的趋势。压比为5时,直接阻尼系数C随栅栏高度的增加越来越大。整体来看,直接阻尼系数C随栅栏高度的变化并不敏感。由图16可以看出不同压比下,直接阻尼系数C随间隙增加呈现先减小后增加的趋势。而在间隙为0.2 mm之后,压比为2和5时直接阻尼系数C是增加的,压比为3和4时直接阻尼系数C是减小的。这是由于间隙增加,流体通过间隙,刷丝束阻碍作用降低,直接阻尼系数C减小,但随间隙增加,流体经过刷丝束后产生涡流,流速减小,直接阻尼系数C增加。

图14 刷束厚度对刷式密封直接阻尼系数C的影响Fig.14 Effect of brush bundle thickness on the direct damping factor C of the brush seal

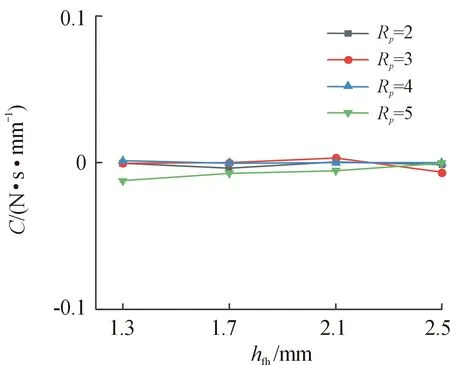
图15 栅栏高度对刷式密封直接阻尼系数C的影响Fig.15 Effect of fence height on the direct damping factor C of the brush seal

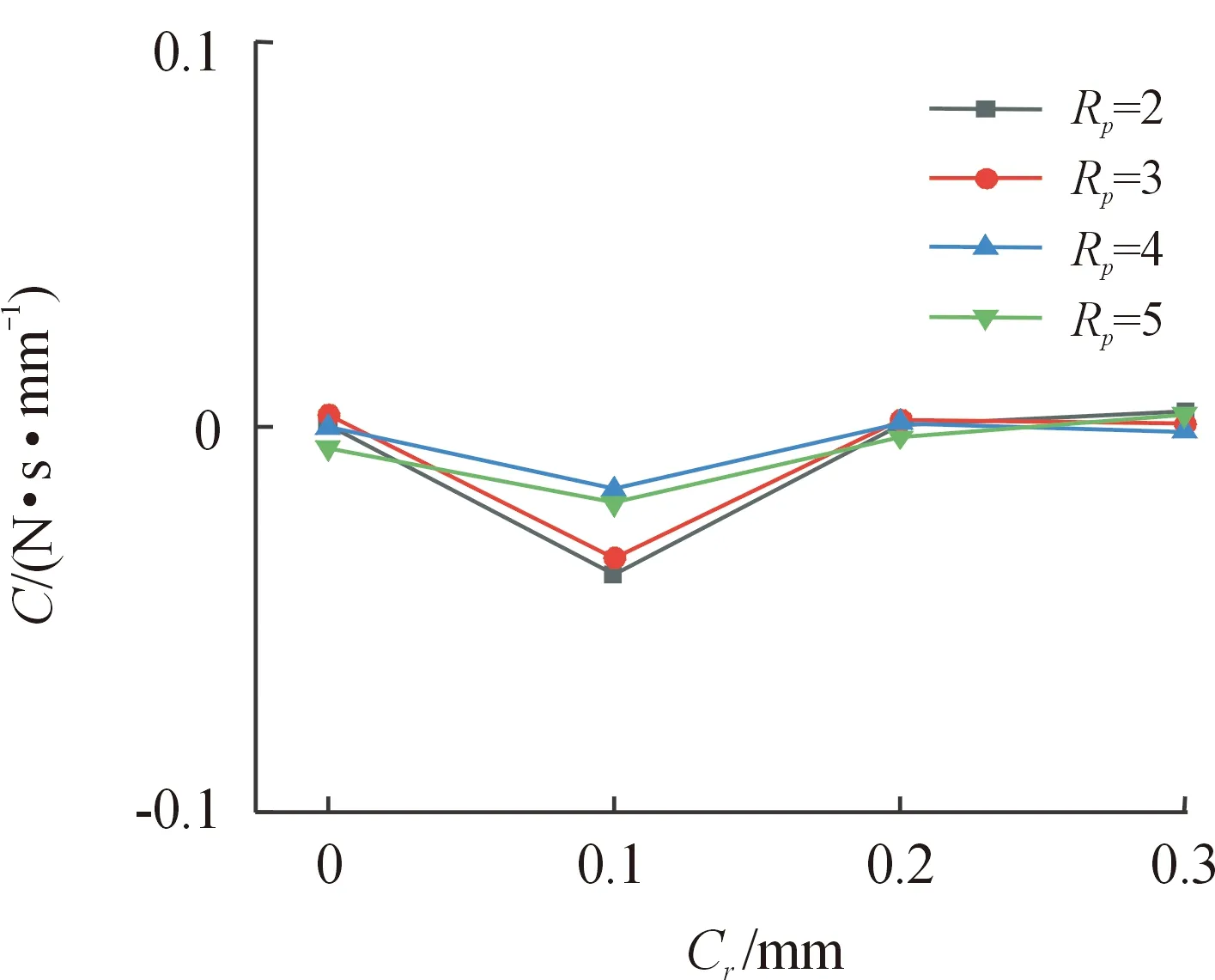
图16 间隙对刷式密封直接阻尼系数C的影响Fig.16 Effect of clearance on the direct damping factor C of the brush seal

4.4 交叉阻尼系数c的影响因素

图17—图19分别给出了直接阻尼系数c在不同压比下随刷束厚度、栅栏高度及间隙增加时的变化规律。由图17可以看出压比为2、3和4时,交叉阻尼系数c随刷束厚度的增加呈现先减小再增加再减小的趋势。而压比为5时,交叉阻尼系数c随刷束厚度的增加而增加。随刷束厚度增加,刷束阻碍作用增加,但交叉阻尼系数随刷束厚度变化并不敏感。由图18可以看出压比为2、4和5时,交叉阻尼系数c随栅栏高度变化并不明显。压比为3时,交叉阻尼系数c随栅栏高度的升高先增加后减小。随栅栏高度增加,交叉刚度系数c呈现无规则的变化。由图19可以看出不同压比下交叉阻尼系数c随间隙的增加呈现先增加后减小再增加的趋势。在间隙为0.1 mm时,交叉阻尼系数最大,并且压比越小数值越大。随间隙增加,交叉阻尼系数c与直接阻尼系数C呈现相反的变化趋势。

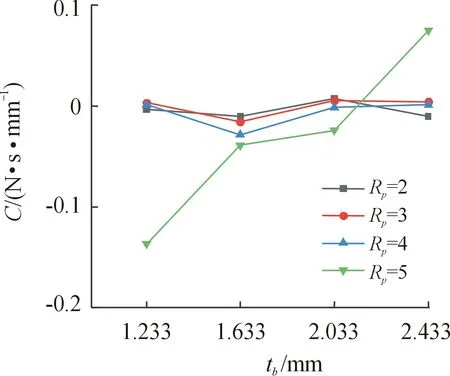
图17 刷束厚度对刷式密封交叉阻尼系数c的影响Fig.17 Effect of brush bundle thickness on brush seal cross damping factor c

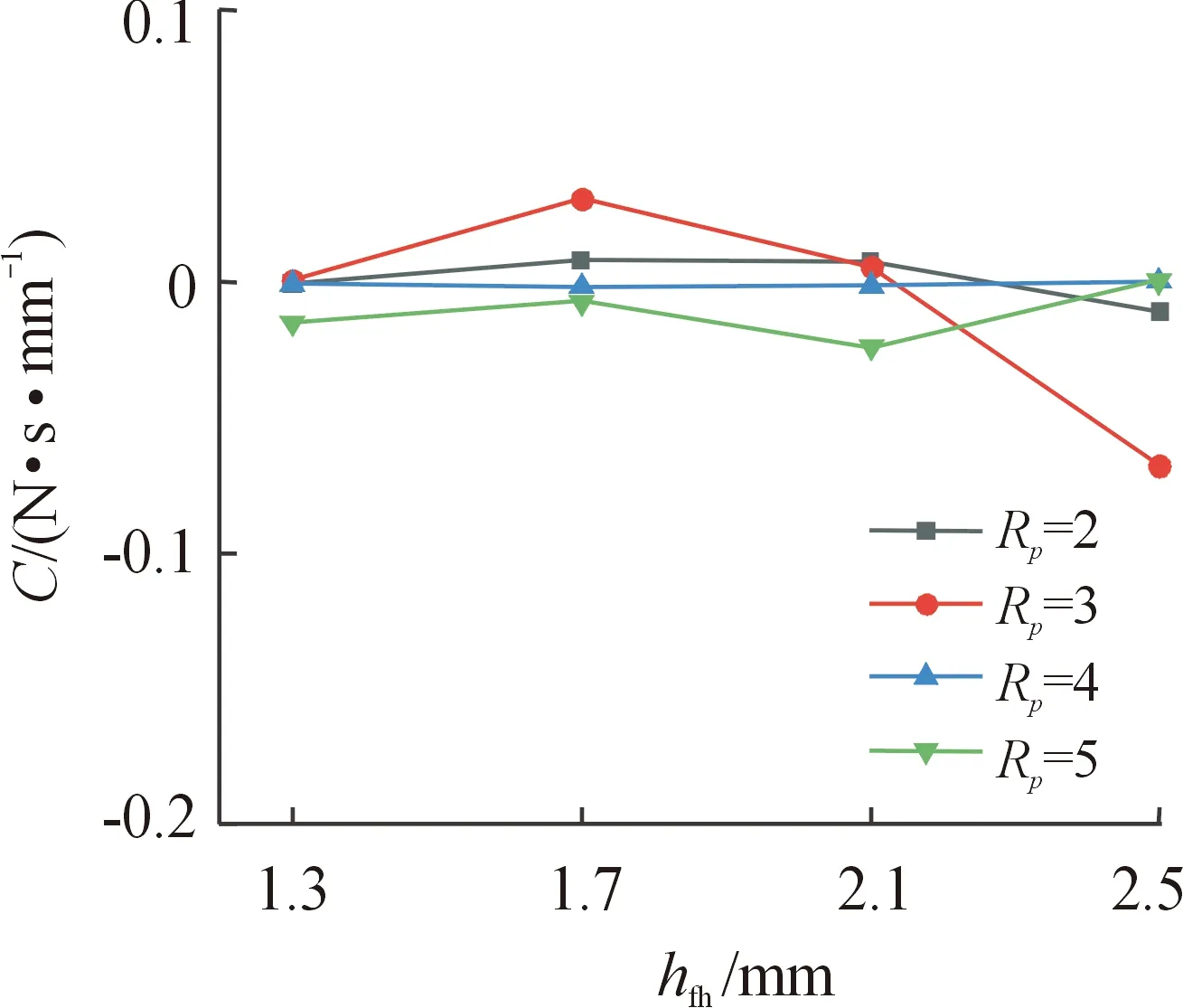
图18 栅栏高度对刷式密封交叉阻尼系数c的影响Fig.18 Effect of fence height on brush seal cross damping factor c

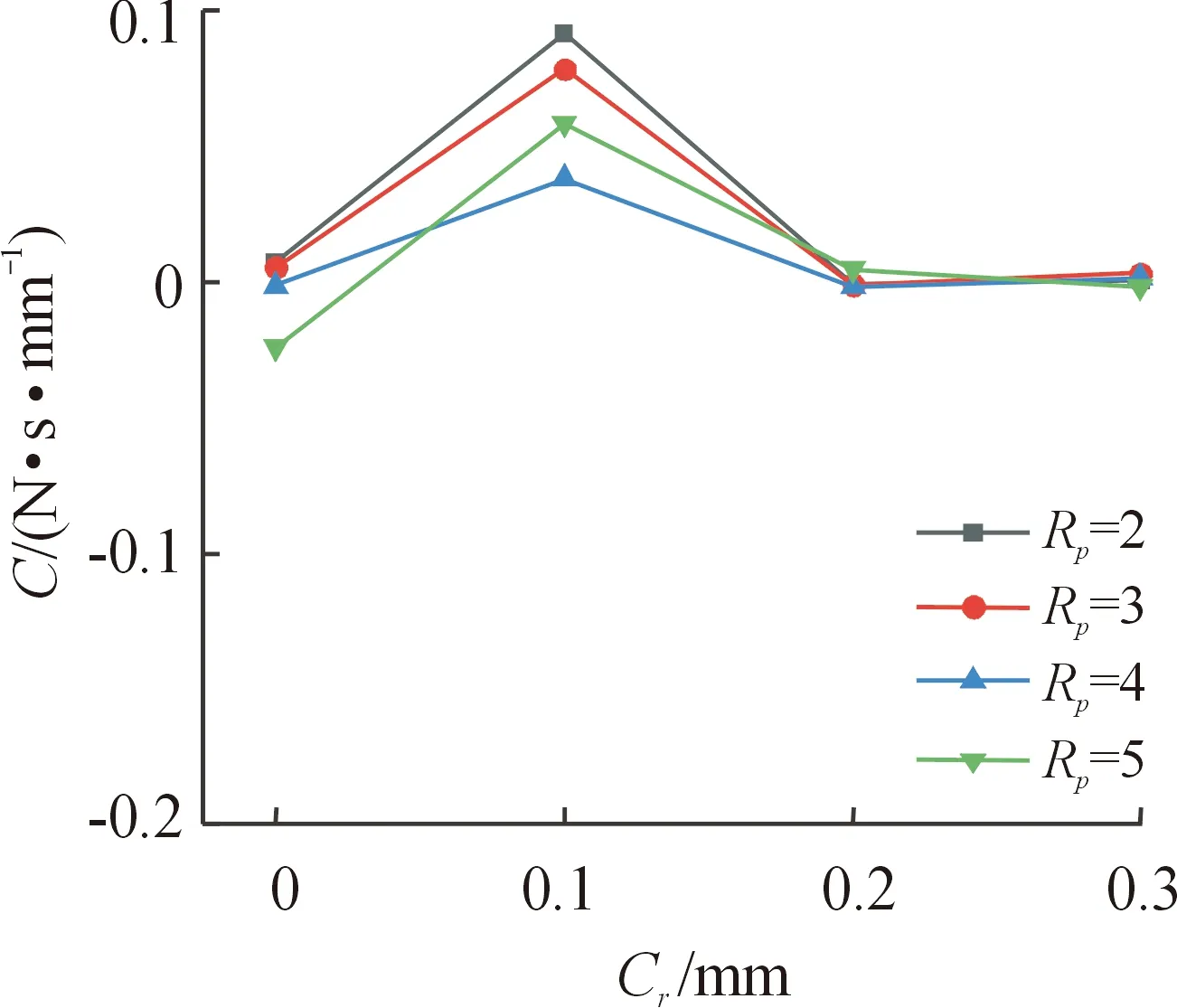
图19 间隙对刷式密封交叉阻尼系数c的影响Fig.19 Effect of clearance on brush seal cross damping factor c

5 结论

研究基于多孔介质LTNE模型建立了刷式密封转子动力特性数值预测模型,研究了不同压比下,不同刷束厚度、栅栏高度和间隙等结构参数对动力特性的影响,得到如下结论:

1) 直接刚度系数K随刷束厚度变化一直是正值,但随着刷束厚度增加,直接刚度系数K整体上在下降;K随栅栏高度增加时从负值增加到正值;当间隙增加时,K从正值下降到负值。K越大,转子系统的最大临界速度越大,系统越不稳定。

2) 交叉刚度系数k随刷束厚度变化时一直是负值;随栅栏高度增加呈现先减小后增加的趋势,整体上是从负值一直降低,直到栅栏高度高于2.1 mm时,k值开始增加一直到正值,压比越大增加的越快;随间隙增加,系数k整体上从负值开始增加到正值,到间隙为0.2 mm时,k值达到最大,然后开始减小。交叉刚度系数k越小系统稳定性越大。

3) 直接阻尼系数C随刷束厚度、栅栏高度变化不明显,敏感度较低影响小。随间隙的增加直接刚度系数C整体上呈现先减小后增加的趋势,但数值都在0值附近变化,因此小于交叉刚度系数k对系统稳定性的影响。

4) 交叉阻尼系数c随刷束厚度的增加在0值附近变化,压比为5时变化较为明显,一直在增加;随栅栏高度无规则性变化;随间隙增加,交叉阻尼系数c呈现先增加后减小趋于0值。交叉阻尼系数c对转子动力系统没有明显的影响。