以应用能力培养为导向的高等数学课程改革初探
赵 蕾
文华学院数学科学系 湖北武汉 430074
高等数学是高等院校理工类专科生必修的重要理论基础课,主要学习函数、一元和多元函数的微分学和积分学、常微分方程、空间解析几何、线性代数和概率论的初步知识及其运用。学生掌握上述知识,能够为学习后续课程奠定良好的数学基础[1-2]。在实际教学中,教师主要是依据大纲要求,在课堂上对于数学基本概念、定理进行讲解和推导,学生主动参与度较低。为提升教学质量,培养学生知识运用能力,把专业学习与动手实践结合起来,全面提高人才培养的市场适应能力,改进教学方法和课程体系,将Matlab软件引入高等数学教学。
Matlab是最近几年应用广泛、计算能力强大的数学计算软件,几乎涵盖了高等数学中大部分计算,学生在大学一年级阶段就可以得到Matlab编程和实践能力的训练,同时在实践过程中促进理论知识的学习[3]。在教学中通过一些实际案例,让学生在计算机中求极限、求函数的微分和积分、函数作图、求解微分方程,这不仅帮助学生更好地理解了教材的知识和定理,又克服了高等数学内容抽象、不直观的不足,提升了教学效果,在实践中激发了学生的学习兴趣,同时提升了学生运用数学知识,解决数学问题能力[4-5]。
一、Matlab在极限教学中的应用
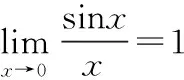
在Matlab中用comet命令生成动态曲线图,输入如下程序:
x=-10:0.01:10;
y=sin(x)./x;
comet(x,y)
axis([-10 10 -1 1.5]);
grid on
运行后,在Matlab中自动生成动态曲线图(如图1所示)。
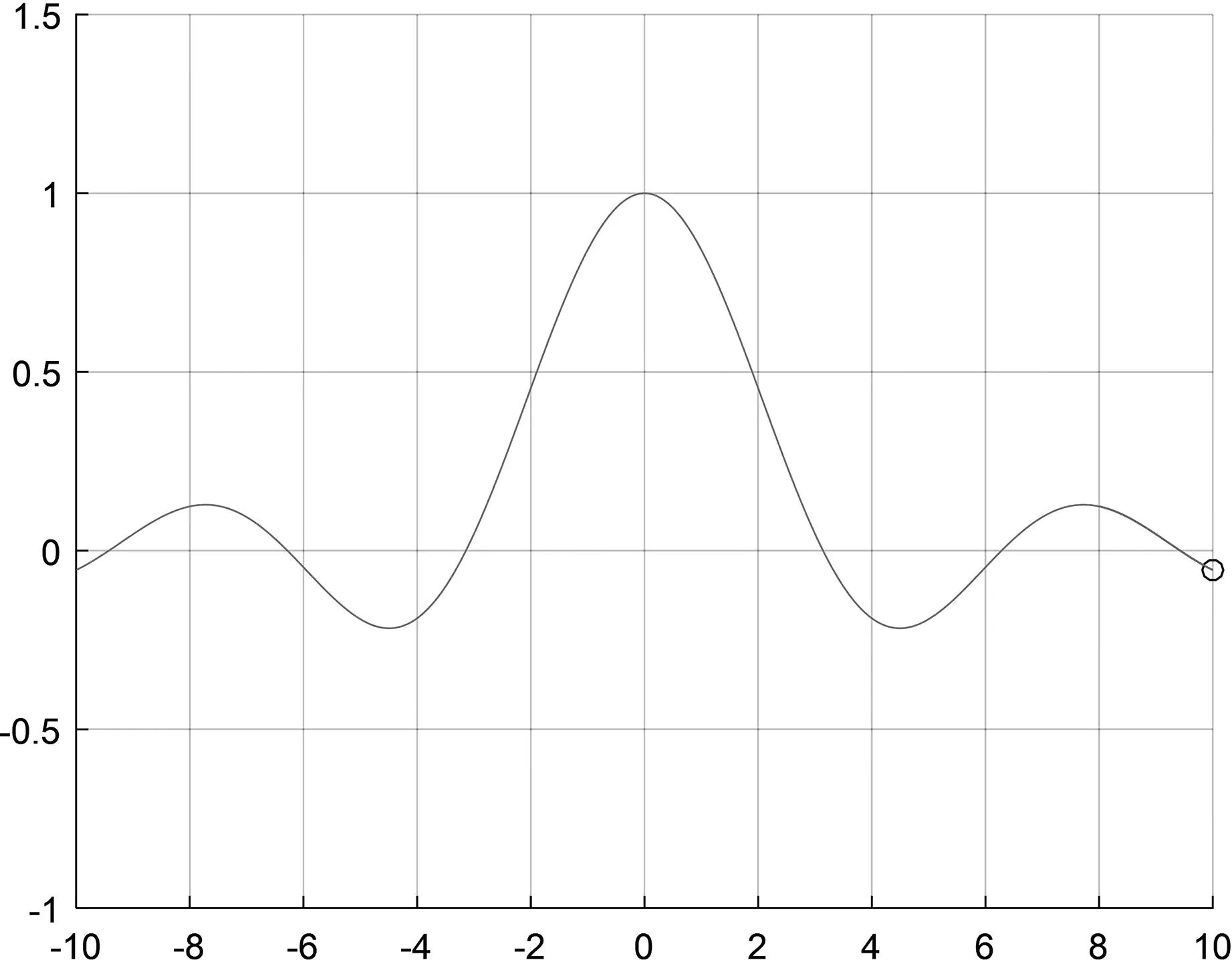
图1 函数的动态曲线图
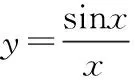
当学生从几何上深刻感知函数值随着自变量取值的变化,教师可以指导学生通过Matlab的limit命令直接计算函数的极限,进一步去计算其他函数的极限。
在Matlab中输入如下程序:
syms x y;
y=sin(x)/x;
limit(y,x,0)
ans =
0
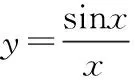
二、Matlab在导数教学中的应用
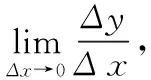
Matlab的diff命令可以直接计算函数的导数,以函数y=x2为例:
例3:求函数y=x2在x=1处的导数,并求出在该点处的切线方程。
在Matlab中输入如下程序:
close all;clear all;clc;
syms x
y=x^2
symDf1=diff(y,x,1);%求解y=x^2的一阶导数Symbolic function
df1=matlabFunction(symDf1);
df1(1)
得到y=x2在x=1处的导数值为2,通过点斜式方程,得到切线在该点的切线方程为y=2x-1。
由于y=x2在x=1处的导数值即为曲线在该点处切线的斜率,为了让学生更好地理解导数的意义,我们选择几个点,通过x→1时割线的位置变化,直观展示出割线的极限即为切线。
首先,通过Matlab程序,在x=1附近选择6个点,分别为(0,0),(0.5,0.52),(0.99,0.992),(1.01,1.012),(1.5,1.52),(2,22),观察x趋于1时,割线的位置变化情况(图2),帮助学生理解导数的几何意义,对切线是割线位置的极限有了更深的认识。
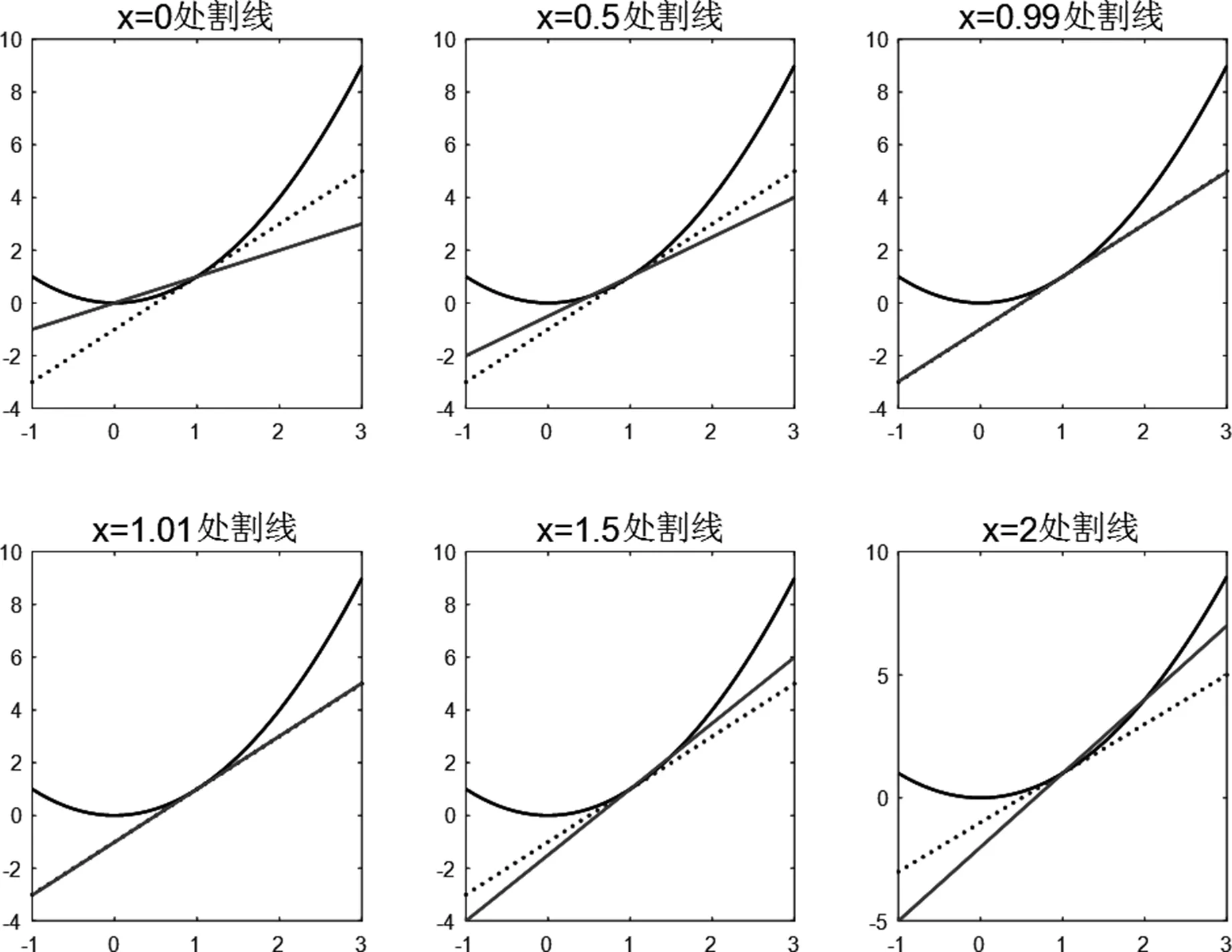
图2 函数y=x2在6个点处的割线(虚线为切线)
从上图可以观察到,x越靠近1,割线越接近切线。进一步验证了导数就是切线的斜率这一结论。
为了提升演示效果,还可以将割线位置接近切线的过程进行动态展示,我们将步长设置为0.1,逐步演示当自变量x从0趋向于1,以及x从2趋向于1时,割线的变化规律(见图3、图4、图5)。
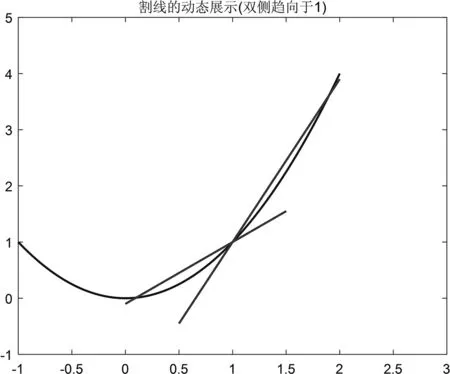
图3 割线的动态展示(初始状态)
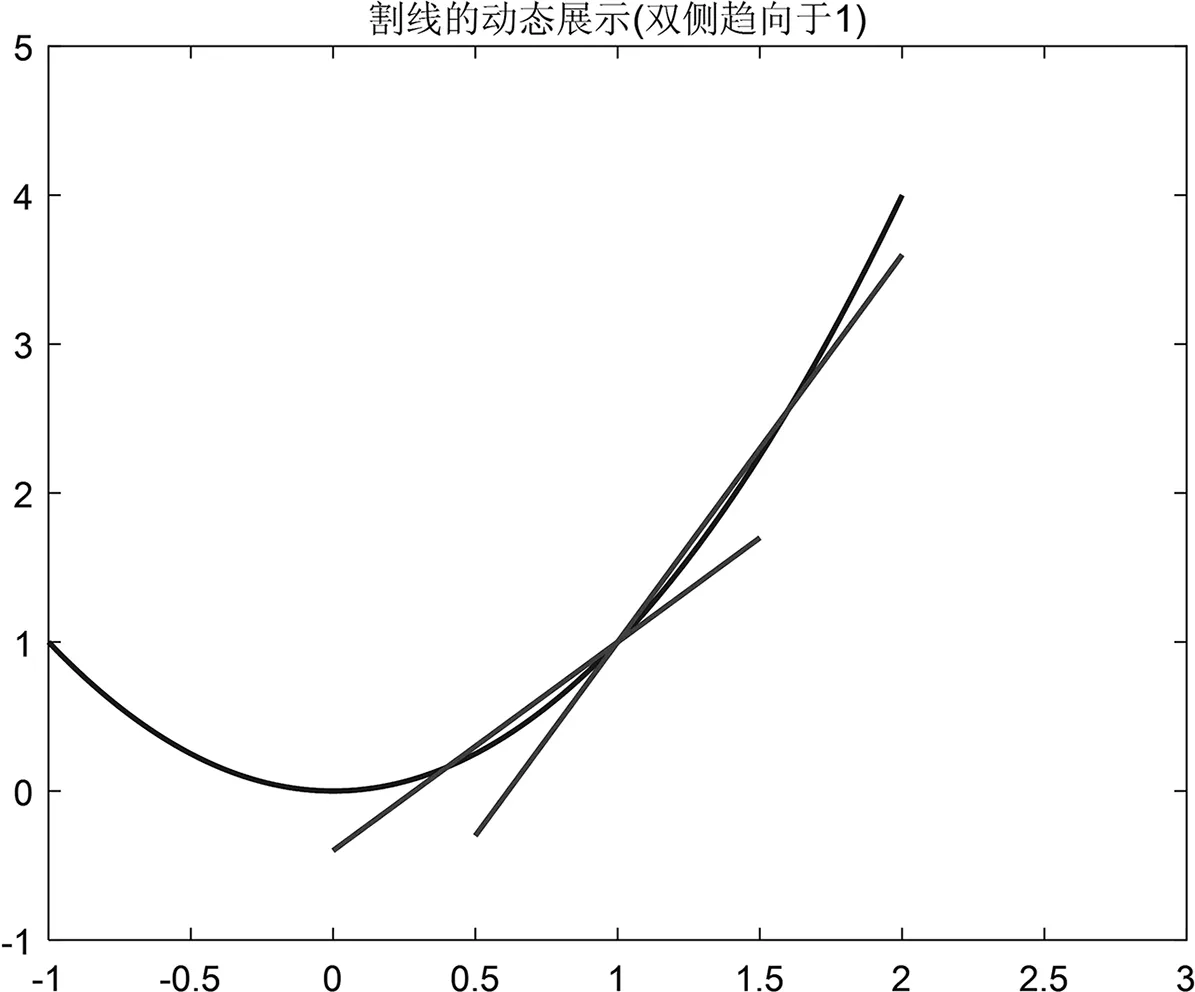
图4 割线的动态展示(5次迭代后)
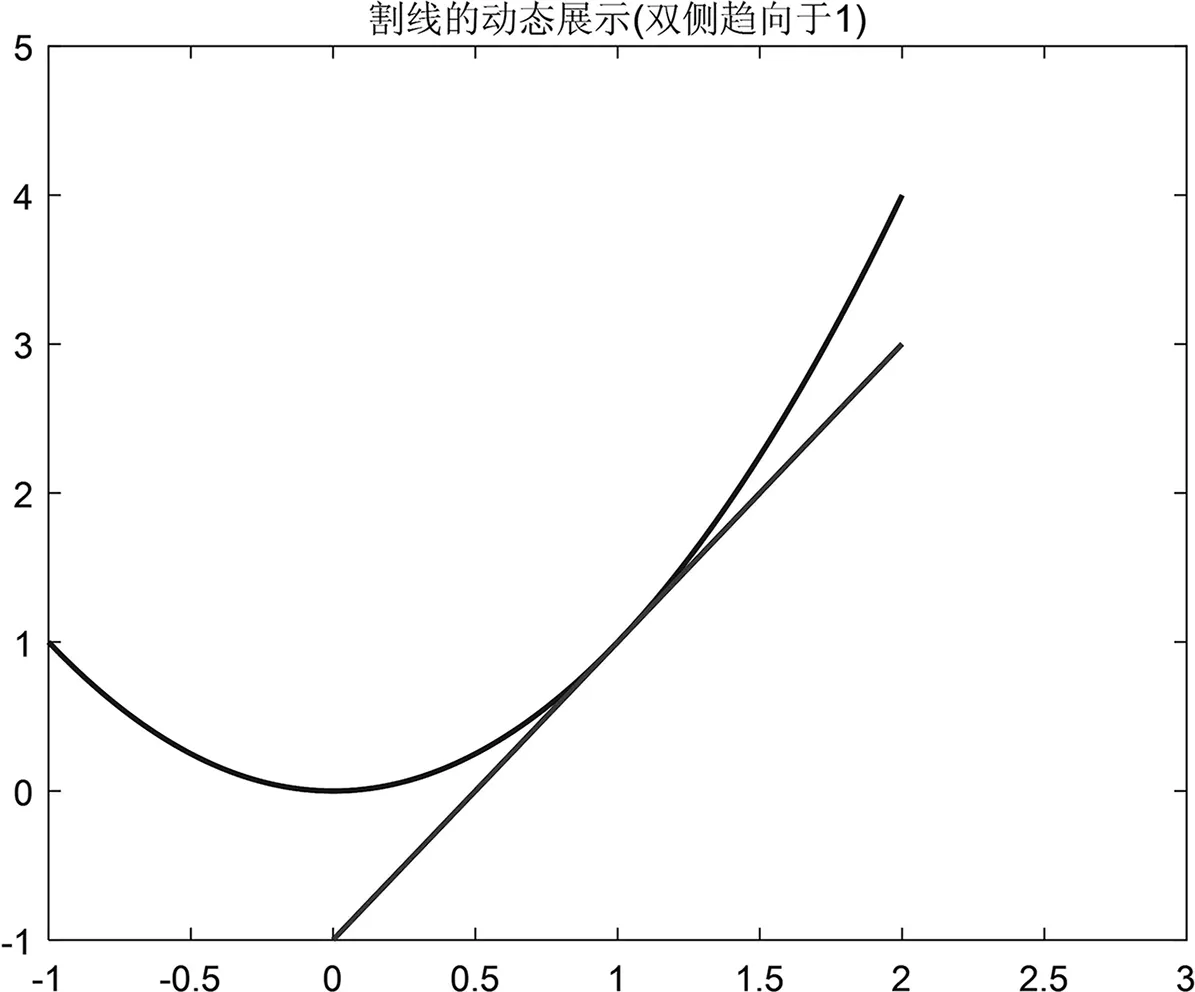
图5 割线的动态展示(最终位置)
在动画展示过程中,学生认识到曲线割线位置的极限即为切线,同时,更深刻地体会到了导数的几何意义,导数是函数的局部性质,对于给定的函数,当函数的自变量和取值都是实数的时候,它在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。通过Matlab的动画演示,我们更清晰地看到数形之间的联系,同时也大大提升了学生的积极性和兴趣,提升了学习效果[8-9]。
三、Matlab在积分教学中的应用
积分是高等数学的一个核心概念,也是需要学生重点掌握的概念,在高等数学教学中,积分主要分为不定积分和定积分两个部分,Matlab软件功能强大,既可以求函数的不定积分,也可以计算函数在指定区间上的定积分。Matlab计算积分是通过int命令实现[7]。
(一)Matlab计算不定积分
在Matlab中输入如下程序:
close all;clear all;clc;
syms x
y=x*exp(x^2)
int(y);
pretty(int(y))
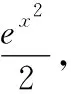
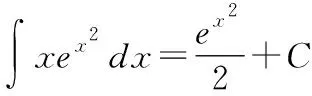
当被积函数中包含由字母表示的数时,要通过Matlab的int(f,v)命令,计算函数f对变量v的不定积分。
在Matlab中输入如下程序:
close all;clear all;clc;
syms x a
y1=1/((a^2+x^2))
y=int(y1,x);
pretty(y)
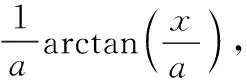
(二)Matlab计算定积分
除了不定积分,Matlab软件也可以计算定积分,通过Matlab的int(f,a,b)命令,求函数f在区间[a,b]上的定积分;当函数f包含由字母表示的数,要通过Matlab的int(f,v,a,b)命令,计算函数f对变量v在区间[a,b]上的定积分。
在Matlab中输入如下程序:
close all;clear all;clc;
syms x
y1=sin(x)
y=int(y1,0,pi);
(三)Matlab通过数值计算方法计算定积分
对于初等函数来讲,虽然原函数存在,但是其原函数不一定都是初等函数,也不一定能够用解析式表达,此时用符号解法计算定积分失效,我们可以通过数值积分去计算定积分的值[10]。
求定积分近似值的方法,教材上通常给出的是矩形法、梯形法和抛物线法(辛普森法),接下来就以一个例子来说明这三种办法求解定积分近似值的过程[1]。
矩形法:
在Matlab中输入如下程序:
dx=0.1;
x=0:dx:1;
y=4./(1+x.^2);
sum(y(1:length(x)-1)*dx)
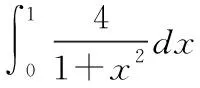
梯形法:
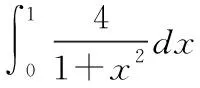
抛物线法:
小曲边梯形的曲边通过抛物线近似,得到小曲边梯形面积的近似值,进一步得到定积分的近似值,在新版本的Matlab软件中可通过integral命令计算:
Matlab程序如下:
y=@(x)4./(1+x.^2);
val=integral(y,0,1,'RelTol',1e-8,'AbsTol',1e-13)
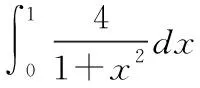
本例所给积分的精确值可以通过int命令直接计算得到:
下表展示了本例积分的精确值及不同数值积分方法计算处的积分值,可见,通过抛物线法(integral命令)得到的精确值最高。
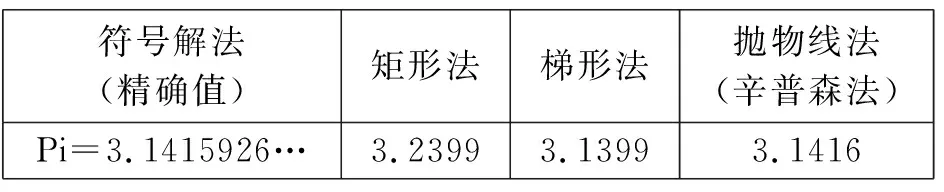
不同数值积分方法得到的结果比较表
一元函数积分学是学好高等数学的基础,在学习过程中,许多同学都会反映有点难度,教师在教授积分方法与技巧的同时,用Matlab软件实现积分计算,不仅可以帮助学生掌握一些积分公式,还可以对积分的结果进行验证。同时,对于复杂函数的积分,当原函数无法用初等函数表示时,我们仍然可以通过数值积分的方法,在Matlab软件上计算出定积分值,在这个过程中加强了学生的学习积极性和学好高等数学的信心。
(四)Matlab计算重积分
在实际问题中,往往要计算与多元函数有关的量,比如计算空间立体的体积、计算曲面面积等,即要把积分加以推广。在高等数学教学中,二重积分是教学的重点也是难点。
当积分区域D为X-型区域时,即当区域为:
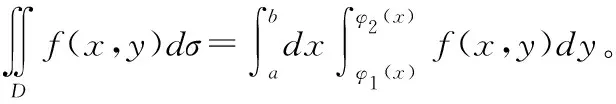
当积分区域D为Y-型区域时,即当区域为:
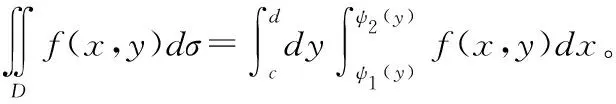
在Matlab软件中可以计算重积分,所用到的命令仍然是int,当积分区域为X-型区域时,Matlab命令为int(int(f,y,φ1(x),φ2(x)),x,a,b),当积分区域为Y-型区域时,Matlab命令为int(int(f,x,ψ1(y),ψ2(y)),y,c,d)。下面以具体例子来说明二重积分的计算。
在Matlab中输入如下程序:
syms x y
f=x*y;
int(int(f,y,0,1-x),x,0,1)
由于积分区域既是X-型区域也是Y-型区域,可以考虑用两种不同的方法求解。
在Matlab中输入如下程序:
syms x y
f=4-2*x-y;
int(int(f,y,-1,1),x,-2,2) 注:将积分区域看作X-型区域。
int(int(f,x,-2,2),y,-1,1) 注:将积分区域看作Y-型区域。
输出结果均为32。
由此可见,Matlab仅仅用一些简单的指令就可以计算重积分,二重积分的计算比一元函数的积分要复杂一点。通过Matlab软件,学生可以直接得到积分值,大大提升了学生的课堂参与度,激发学生学习的兴趣,对于计算机软件的运用能力也得到了提升。
四、Matlab在微分方程教学中的应用
函数是微积分的研究对象,反映了客观事物的内在联系,在科学研究和生产实际问题中,寻找事物间的函数关系非常重要,但很多情况下,函数关系不能直接得到,而是根据问题情境,列出未知函数及其导数的关系式,这样的关系式即为微分方程,当未知函数为一元函数时,即为常微分方程。随着科技进步与发展,物理、经济、金融、航空航天等众多领域的问题都可以描述为常微分方程,因此它的运用也非常广泛。在教学过程中,教师要引导学生不断探索和发现生活中的数学问题,通过微分方程,建立数学模型去描述、分析和解决实际问题,提升数学知识的应用能力。
Matlab软件求解常微分方程,得到微分方程的符号解,是通过dsolve命令实现的[11]。
在Matlab中输入如下程序:
syms y(x)
y(x)=dsolve(diff(y,x)==2*x*y)
得到结果为y=Cex2。
例11:求微分方程y″+2y′+y=0满足初始条件y(0)=4,y′(0)=-2的特解。
在Matlab中输入如下程序:
syms y(x)
Dy=diff(y);
y(x)=dsolve(diff(y,x,2)+2* diff(y,x)+y==0,y(0)==4,Dy(0)==-2)
得到结果为y(x)=4e-x+2xe-x
在教学过程中,我们讲到不同类型的微分方程,如可分离变量的微分方程、齐次方程、一阶线性微分方程、二阶常系数齐次线性微分方程等,对于不同类型的微分方程,有不同的解题方法,因此常微分方程既是教学重点,也是难点。Matlab功能强大,可以通过dsolve命令计算出微分方程的解析解,计算准确,运行效率高。将Matlab与高等数学教学结合起来,学生可以将手工计算的结果进行验证,提升了教学质量和教学效果。
结语
在专科高等数学教学中引入Matlab软件,在保持原有教学体系不变的前提下,弱化定理的证明和逻辑推导,通过设计和专业知识相结合的案例,让学生在实践中学到了知识,即克服了教学内容抽象、不直观的不足,又让学生逐步学会Matlab软件使用和操作方法,增强了学生的实践能力和应用能力,感知数学美,进一步增强学好数学的自信心。

