欠驱动式柔性轮足机器人的腿部结构及步态设计

杨童磊 王庆礼 康 华 谢丽辉

江西理工大学能源与机械工程学院 江西南昌 330000

轮足机器人兼具轮式移动平台的快速性和足式移动平台在非结构化环境中的强适应能力,在军事、灾害救援、野外作业、家居服务等领域有广泛的应用前景。轮足机器人作为一种新型的移动平台,通常基于仿生腿部和轮足结合方式,既保持轮式平地运动能力,又通过多自由度的腿部设计和离散的落足点,使机器人在可达空间内选择最优支撑点,拥有较强的越障能力,并能实现躯干质心运动轨迹与足端轨迹解耦,保证了在崎岖路面上运动的稳定性。研究表明,轮足机器人在非结构环境运行中能耗效率、移动速度和负载能力方面相对于其他运动形式和复合移动形式的机器人具有更优异的表现[1]。

将轮足装于多关节足式结构末端是最常见的布置形式,2018年以来苏黎世联邦理工学院的研究验证了一种基于机器狗ANYmal基础上衍生轮足复合式移动机器人,根据每条腿的轮子运动的效用在滚动和步态之间无缝转换,实现高度动态的运动[2];基于Stewart平台的六自由度并联机构的六足轮足机器人[3-4]是学者关注的另一种典型结构形式,六个可调节腿类似于并联机械手,提供具有高精确运动及多点稳定支撑;此外,采用可缩回模块的轮—腿可变形的结构设计,既可作为轮子也可作为腿足,提高了在复杂环境中的运动性能和通过性能[5-6]。上述轮足设计结构都具备良好的地形适应能力和机动性能,但其结构方案及其运动策略在灵活性、稳定性、越障能力、负载能力及运动规划求解效率等方面存在不同程度的问题,需进一步分析评估。

本文提出一种仿蜘蛛腿部的具备良好运动性能、控制策略简单的四足轮足机器人移动平台。机器人整体采用腿部位于躯干两侧,质心低、支撑面积大、静态稳定性高的布置形式[7];腿部机械结构采用欠驱动并联式柔性多连杆机构形式,能够保持较快运动速度和较强的越障能力,简化运动控制策略,控制简单算法高效,且柔性杆件结构能起到减震作用。

1 轮足式机器人结构

该轮足式四足机器人主要由底盘和轮足式腿部结构、驱动舵轮、控制模块、上位机模块、传感器模块、电源模块、安装在躯体上方的旋测云台机构以及激光雷达等组成。为增加机器人支撑面积,增加机器人稳定性,轮足式腿部结构采用仿爬行动物式布局方式,对称分布在躯体两侧。四足轮足式机器人整体布置如图1所示。

1.腿部连杆机构;2.减震元件;3.直驱车轮;4.移动底盘图1 轮腿式机器人整机模型

2 轮足式机器人腿部结构设计

该腿部结构是该机器人的关键部件,出于对机器人腿部电机负重的实际需求,对关节型腿部结构进行改进,利用机械连杆机构简化腿部驱动,如图2所示。

图2 欠驱动腿部结构简图

机器人腿部行走部分都采用一个髋关节转动副和一个平行四连杆机构来实现。每条腿有两个自由度,在腿部结构髋关节和膝关节分别安装一枚伺服电机,可以进行0°～180°的双向转动。髋关节完成机器人腿部的前后摆动,膝关节完成腿部的上下移动,两个方向的自由度可以使得机器人腿部完成基本的步行动作;平行四连杆机构保证小腿垂直运动,辅助机器人能完成连贯的欠驱动式行走,提高动作连贯性,增强越障能力;足部直流驱动舵轮配合腿部装置,使得机器人兼具轮式快速移动能力。

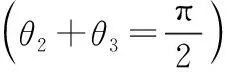
3 轮足机器人腿部结构运动学分析

针对此机器人的腿部结构,单条机械腿可视为一组欠驱动串联机械臂,利用前置D-H法建立腿部结构的运动学模型及位姿正、逆求解,建立起机器人姿态与驱动电机转角的运动学关系,利用Matlab进行仿真验证与分析。

3.1 基于改进D-H法的腿部运动学模型

3.1.1 D-H坐标系建立

根据改进型D-H法的坐标系构造原则,以各旋转关节旋转轴或直线关节运动方向为相应的Z轴,沿连杆方向为X轴,通过右手定则确定Y轴,分别构建机器人右前腿机构的坐标系。各杆长设为L1,L2,L3,L4,L5,各转动关节转角设为θ1,θ2,θ3,通过D-H法坐标系得到D-H参数表,见表1。

表1 模型D-H参数表

改进D-H法可以采用齐次矩阵的形式表示出坐标系i-1与坐标系i的变换关系,为了使公式简洁,约定sinθ=Sθ、cosθ=Cθ。坐标系i-1与坐标系i变换矩阵可表示为式(1)。

(1)

3.1.2 位姿变换矩阵与腿部D-H模型

由此,可得坐标系1到坐标系0、坐标系2到坐标系1、坐标系3到坐标系2、坐标系4到坐标系3的齐次变换矩阵。通过上述四个齐次变换矩阵的点乘可得到关节末端相对于固定坐标系的位姿变换矩阵:

(2)

坐标系4到坐标系0的旋转变换矩阵为:

(3)

其中,n为X坐标系旋转矩阵,o为Y坐标系旋转矩阵,α为Z坐标系旋转矩阵:

(4)

代入尺寸参数,由此得到机器人腿部空间位置与电机运动参数件的运动学模型,表达式为式(5)所示:

(5)

3.1.3 基于Matlab足端位姿矩阵求解

为验证该腿部结构模型的有效性,基于Matlab的Robotic工具箱的模拟仿真功能进行验证。通过在Robotic工具箱中构建的仿真机械腿,将初始θ1设定为0,θ2值设定为-π/4,θ3设定为3π/4,通过转换方程(5)可解算出关节角与足端位姿关系,模拟仿真可分析机器人腿部结构运动,如图3所示。

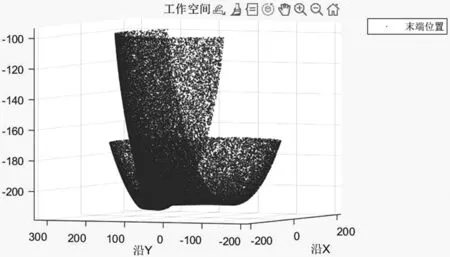
(b)工作空间点阵图图3 腿部结构运动姿态仿真

如将表达式(5)中机械腿部实际D-H参数设定θ1=0、θ2=π/4,可得到机器人腿部末端的位姿,即X=225.77,Y=0,Z=-69.43。结果表明,当电机参数θ1、θ2确定时机器人腿部结构末端唯一确定,Matlab的仿真结果和机械腿部结构位姿的描述吻合,验证了机器人腿部结构模型具有运动姿态变化的可行性。

3.2 腿部结构工作空间分析

在多足机器人的运动学分析中,腿部结构的工作空间是多足机器人运动学分析中不可或缺的一环,是步态分析的基础。根据表达式(5),通过机器人腿部结构末端的位姿矩阵结合具体参数,可以得到机械腿末端相对于腿部固定起始端的空间相对位置。

在Matlab的仿真环境中结合几何约束,采用蒙特卡洛法,通过随机在三维空间中创建一百万个可达点,可得到机械腿部末端的工作空间点阵图,如图3(b)。可以看出,机器人腿部运动轨迹是有规律的弧线运动,其工作空间将呈现空间多弧面交叠的状态。欠驱动式的结构使得机器人腿部转角θ2、θ3之间拥有线性关系,即:θ2+θ3=π/2,将使三个关节驱动参数变为两个关节驱动参数θ1和θ2,降低了腿部结构的自由度降低,控制简单,求解效率更高,且在工作空间内该轮足腿部结构具有足够的灵活性。

4 轮足式机器人的步态规划及稳定性分析

为保证轮足式机器人能够进行稳定的运动,对机器人进行步态规划,以实现机器人的稳定周期性运动。多足机器人步态规划主要内容包括足端轨迹规划,以及协调好多足之间运动相对时序关系,即步态时序。足端运动轨迹通常包括悬空相轨迹和支撑相轨迹,这两个特征可以基本描述机器人单腿的运动状态。空悬轨迹相数与总轨迹相数之比称为占空比β,通过四足机器人的占空比β,将四足机器人的运动步态划分为静态步态0.75≤β≤1,准静态步态0.5≤β≤0.75,以及动态步态0≤β≤0.5。

腿足机器人采取仿爬行动物式构造,步态规划主要采取静态步态规划,即在步行过程中每一时刻都至少有三条足处在支撑相,即三点支撑。根据静态稳定边界法(Static Stability Margin,SSM),可初步得到机器人行进时跨距大小ΔL应不大于机器人身体长度L的一半,即满足ΔL≤L/2;而由Qu Meng-ke等人的研究可知,当达到一定稳定裕度时,机器人行走速度越快,所消耗的能量越少,该步态就越佳[8],而在一个周期中机器人行进速度与跨步大小成正比。考虑到机器人功能的实际需求,取机器人迈步长度为机器人主体长度(L=300mm)的一半,即取ΔL=L/2=150mm。

为满足机器人的运动需求将设计三种腿的支撑相T1、T2、T3,如图4所示三支撑相示意图。

(a)三支撑相

(b)单个周期行走步态时序图4 腿部支撑相

(6)

因而根据机器人移动时每个位姿对应的足部相位(末端坐标),便可得到单个周期内的机器人移动六种步态及腿部相序。从图4(b)单周期内步态时序图可以看到,移动步态所对应腿部支撑相,而支撑相对应的腿部末端的X、Y坐标位置可由方程组(5)逆求解,得到电机运动参数θ1和θ2,实现对轮足机器人行走的步态规划。

采用规范化能量稳定边界法[9](Normalized Energy Stability Margin,NESM),充分考虑了构建机器人质心与支撑多边形几何位置、外界势能的影响和质量影响,能更准确地描述机器人在崎岖路面上行走的稳定性判别方法。该方法中,质心p点到p′的高度hij所克服的最小势能,为稳定裕度法对应边lij的稳定裕度SESM,表达式可表示为式(7)。

(7)

进行规范化处理:

(8)

在机器人仿真模型上通过SolidWorks建立仿真模型及ESM边界,利用传感器功能分别追踪轮足式机器人在步态1和步态2状态的质心位置及相关参数,可计算机器人周期步态的规范化能量稳定裕度,见表2。

表2 各步态能量稳定裕度

通过表2可以看出,规范化能量稳定裕度即机器人在一个周期每个步态的倾覆所需要的最小势能高度,如步态1中机器人在水平面上运动时整个周期步态中机体上升高度应小于6.06mm,以避免势能过高导致倾覆的可能。保证规范化能量稳定裕度在边界范围,即可保证机器人周期步态的足够稳定性。

结语

本文提出了一种新型四足轮足机器人移动平台,进行了机器人腿部结构模型的设计与运动学模型推导,在此基础上求解出腿部结构的运动空间,并以此运动空间及稳定裕度两个方向为基准,设计出一套新的四足机器人步态。

本文提出的四足式结构,采用欠驱动并联式柔性连杆结构形式,既具备快运动速度和较强的越障能力,也具有运动模型简单、运动控制策略简化的优点。通过仿真结果表明,该移动平台具有较好的稳定性及可行性,可为轮足机器人的设计和应用提供参考,后续拟通过样机制作对该轮足机器人方案进行进一步运动特定验证和方案优化。