数学课程资源建设探索研究

倪新东 吴嘉琳 王海兰

衡阳师范学院南岳学院数学与计算科学系 湖南衡阳 421200

数学课程的教学资源比较缺乏。好的教学资源是教师精心准备的,随着课时以及需求不断更新的。拥有好的课上课下教学资源,对于学生和老师而言在课上都会更加轻松。目前一些教学资源已经可以由教师通过雨课堂这种在课堂上与学生产生即时互动。借助一些开源工具,可以让学生接触到高质量的数学课程资源。教师可以通过多种方式来展示课程资源,从而丰富教学活动形式,提高教学质量,进而促进学生各方面的发展。

徐继存等认为课程资源的开发与利用不能随意而行,应遵循开放性原则、经济性原则、针对性原则和个性原则。教师可以采用实践——体验、问题——探究和情境——陶冶等方式引入课程资源[1]。

王爱玲教授认为教师要开发数学课程资源,一要合理拓宽数学教材资源,用“活”教材;二要积极开发软件和网络资源;三要充分挖掘数学中的人力资源;四要整合学科综合资源;五要善于利用学生生活中的数学资源[2]。其中第三点挖掘数学中的人力资源主要是以学生为中心。第四点整合学科综合资源是将语文、英文、化学等各科知识综合起来。

吴刚平等认为首先要解决课程资源建设中的三个问题:一是教材不是唯一的课程资源,二是教师是最重要的课程资源,三是课程资源的建设必须纳入课程改革计划[3]。

1 文字资源、实物资源、活动资源和信息化资源

根据物理特性和呈现方式,课程资源可分为文字资源、实物资源、活动资源和信息化资源。

1.1 文字资源

随着社会经济的发展,大部分的学生更希望遇到通俗易懂的教材,而不是一本关于这门科目的字典。所以推荐一些经典的纸质教材是非常有必要的。Gilbert Strang教授的《线性代数导论》可以配合对应的公开课的视频使用。David C.Lay编写的《线性代数及其应用》或对应的中文翻译版本也是十分优秀的教材。另外有一些讲义、书评、杂文等都可以作为文字资源使用。

1.2 实物资源

在讲解立体几何时可以利用的实物资源包括教室里的三面墙则刚好可以充当三个坐标平面。在讲直线方程的时候,可以拿一根长长的棍子作为演示。在讲直线方程的一般形式时,打开一本书,书脊刚好构成书封面形成的两个平面的交线。可惜解析几何中其他常见的曲面则没有能够买到的模型,只有圆柱体等中小学中常见模型。

1.3 活动资源

活动资源也是十分重要的。老师的某些言语可能无形之中影响了学生,造成学生的学习兴趣下降。相反,如果多鼓励学生,那么学生的积极性会变得更强。

1.4 信息化资源

信息化资源建设是有无限发展空间的,其包含的形式也非常多。

1.4.1 电子教材

学校购买的教材部分包含电子资源,这样学生回家可以不带纸质教材。如韩旭里、谢永钦主编的《概率论与数理统计》教材可以在书中的二维码扫码得到正版的电子资源。Dr.Gregory Hartman等教授编写的著名的APEXCalculus。在线互动式的英文线性代数教材InteractiveLinearAlgebra,里面有一些可以交互的资源。Jim Hefferon教授的LinearAlgebra,与《线性代数应该这样学》对应的Sergei Treil教授的LinearAlgebraDoneWrong内容也都十分丰富。

1.4.2 网易公开课、慕课等视频形式

网易公开课中与数学公共课相关的视频有麻省理工Gilbert Strang教授的《线性代数》,麻省理工Denis Auroux教授的《多变量微积分》。这些视频教室里有学生在场也比较有代入感。

中国大学慕课国家精品课程中对应同济大学第七版的高等数学有浙江大学苏德矿教授的《微积分》。苏教授的课程内容丰富,知识点讲得特别详细,对于学习难度比较大的同学有帮助,非常适合理工科的同学。

其他课程比如有可汗学院,但因为是英文的视频,没有字幕,所以学生使用起来比较困难。

1.4.3 传统的办公软件及其与学习通、雨课堂的结合

使用传统的办公软件制作课程资源是非常高效率的。学习通与雨课堂在近几年线上教学与线上线下混合式教学中起到十分重要的作用。二者可以在教学的过程中与学生产生互动。雨课堂可以让学生在教学过程中发弹幕来与教师进行交流。学习通在课后能够为师生们提供方便。老师们可以掌握同学们的学习进度,查看作业和布置考试。

1.4.4 Geogebra等可视化演示

在解释微积分的定义过程中,使用geogebra的课程资源动态地展现这个极限的过程是非常有意思的,学生的兴趣也很好。这个软件的优点包括开源免费,有接口支持自己二次开发,有其他作者已经制作好了的丰富的课堂资源,等等。

使用geogebra嵌入网页可以制作出自己风格的网页,积极开发软件和网络资源。因为是自己制作的网页,可以离线使用,适用于网络信号不稳定的时候。这与教室里的电脑可能不兼容自己制作的资源一样,有时需要自己带电脑去教室以确保教学教程正常开展以及达到设定的教学效果。在讲解高等数学(下)空间解析几何部分时可以把直线、平面以及很多类型的曲面都用geogebra嵌入网页里展示。

与geogebra类似的还有desmos,几何画板等。Desmos与geogebra功能十分类似,但不具有二次开发的功能。而几何画板是付费软件,使用起来不是很方便。

同样用于可视化演示的还有blender、3dmax等三维软件。其中blender是开源的,而且有比较多的教程。图1是用blender展示求z=xy与x2+y2≤1所围成的曲面的表面积时的三维动画截图。

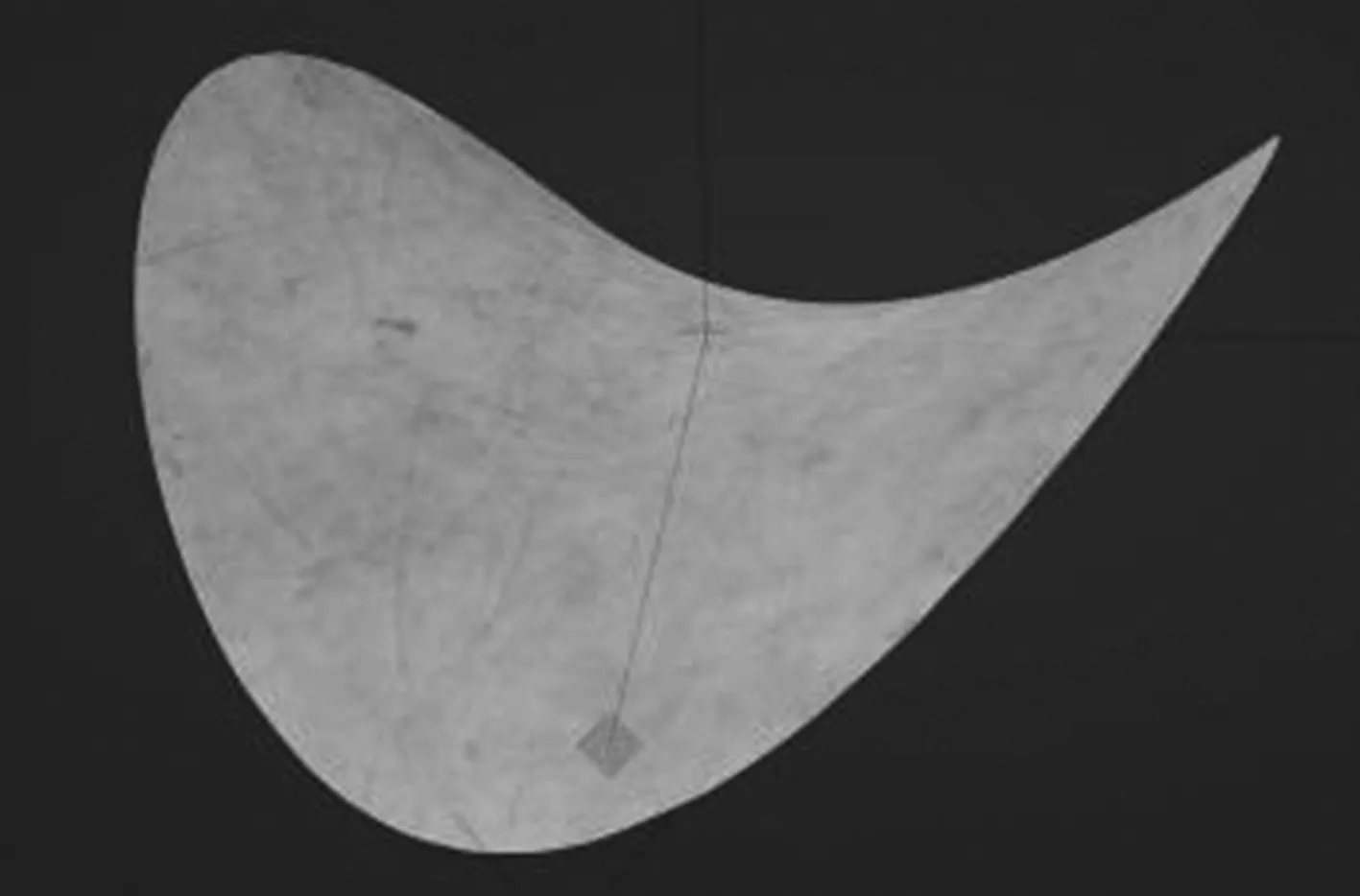
图1 求曲面表面积的动画截图

1.4.5 3Blue1Brown开发的制作视频的工具及其视频

3Blue1Brown账号的作者Grant Sanderson老师基于Python开发的开源视频动画制作工具manim是一个非常有吸引力的工具。大量的学生能从其视频中直观地感觉到微积分、线性代数的本质。也有很多视频创作者借助于manim做出了非常出色的数学知识视频。不过manim软件安装使用起来有一些复杂。

1.4.6 LaTeX资源

使用LaTeX工具可以很方便地开发出优秀的课程资源。其制作的beamer功能上类似于PPT。其优点是稳定、跨平台,不同设备使用起来效果一致,等等。LaTeX中包含的宏包可以让老师方便地完成复杂形式的素材,比如借助siunitx宏包可以产生国际单位制中的符号,借助exam宏包可以制作试卷,借助tikz、pgfplots宏包可以画出融入文本的各种图形。网络上也有很多制作好的素材,对此进行学习或者编辑可以方便得到自己想要的素材,并再次分享出去供别人使用。

1.4.7 使用asymptote等制作图形

Asymptote一词名为渐近线,在此特指这个绘图工具。除了有非常丰富的案例用于学习,很多老师也用这些工具来绘图。Samuel S.Watson教授在多元微积分中用asymptote所画的图也十分漂亮。在讲解拉格朗日乘数法时,为了展示极值点处条件函数的梯度与目标函数的梯度是平行时,利用Inkscape制作了矢量图[4]。

1.4.8 markdown等程序的使用

借助LaTeX相关的markdown可以方便地制作出含数学公式等丰富内容的课程资源。使用vscode中的插件还能生成html等易浏览的文件。在线上教学的时候,不太好使用板书的时候,可以用vscode写markdown代替用鼠标手写。MathJax则可以生成网页上的公式,而且stackexchange上公式的动态展示就是用的这个JavaScript工具。

1.4.9 计算工具

一些计算工具可以推荐给学生,方便学生课下核对答案等。Wolfram Alpha求平方函数在0到1上的定积分可以通过输入integrate x^2 from 0 to 1得到。

线性代数中的一些计算可以通过octave来实现。学生可以在课下时检验自己计算是否正确。老师也可以在课上已经讲过一些题目的计算后,跳过一些类似的计算过程,由学生们课下推导,并用octave检验。

1.4.10 问答网站

还有一些数学类型的问答网站可以推荐给学生课下使用。中文社区的包括哆嗒数学网、博士论坛等。英文的问答网站有stackexchange下的mathoverflow与math.stackexchange。

1.4.11 自媒体

现在很多人会做自媒体来分享自己的知识,比如微博里浙江大学的苏德矿教授的账号矿爷课堂经常给学生答疑。南京大学的朱富海教授的公众号会发布启发学生的内容。北京大学周兰珺个人公众号会发布一些具有启发性的物理与数学方面的问题,比如泰勒展开影响质点自由吗?还有更多地分享题目、题型、试卷的自媒体。

2 数学课程资源建设以及数学课程资源探索

2.1 基本的教学资源

2.1.1 教学课件的制作

为了方便改写与获得较好的数学公式的展示效果,采用了LaTeX的beamer来制作教学课件。虽然传统办公软件可用素材很多,但LaTeX可用的宏包也多,例如上面提到的tikz宏包用于绘图。图2就是一个使用tikz与pgfplogts宏包制作的图形。

图2 求阴影部分的面积

2.1.2 平时作业与测试的编写

如果是编写一个题目,可以使用tikz的standalone宏包。再截图放到学习通里,这样的效果比较好。如果是很多题目,则自定义一个模板类,这样可以使用自己beamer讲义中的资源。学校的试卷模板就写过一个LaTeX版本的。

2.1.3 答案的制作

答案与测试的编写都可以使用LaTeX中的exam宏包。宏包作者Philip S.Hirschhorn教授将答案可以调颜色高亮显示是一个非常不错的功能,很容易辨别题目与答案部分。

新版Word或WPS都很容易编辑公式了,但适配不同的电脑还是有很大的问题。

2.2 值得学习探索的教学资源

我们可能还会时不时遇见让人眼前一亮的教学资源。虽然有些资源可能不是特别适合课堂教学,但是也可以给我们一些启发。

2.2.1 独特的视频效果

北师大李老师在视频网站上传的关于高等代数等的视频所呈现出来的效果是李老师站在玻璃的后面,用手指着玻璃上彩色签字笔写的知识点并讲解。这种形式特别有意思,相信同学们学起来很有劲,这是一个让人感动惊喜的实物资源与电子资源。

2.2.2 使用手动PPT

罗永浩先生在某场辩论上使用了手动PPT的方法,即拿着很多大纸板,上面写着一些观点和数据。它基本起到了一个PPT的作用。这种方式给了我很大启发,我也偶尔使用,学生应该能有很深的印象。这是一个不太容易想到或实施的实物资源。

2.2.3 塞尔达讲物理、图寻学地理

借助年轻人感兴趣的东西与学生交流,可能会事半功倍。我看到过利用塞尔达讲解小船过河问题,利用图寻找到街景中的地理要素并指出该地区位于哪里来学习地理。自己坐在很多钉子上解释关于压强的知识,这一系列很特别的教学视频也给我们带来启发。

概率论中有一个经典的三羊问题,在课上讲解三羊问题应该是非常常见的教学内容,但是让学生们怎么参与进来,可能需要一些探索。现在有很多程序可以做到实时游玩,而且保证了可操作性、随机性。我在线上上课的时候,就曾经让同学体验过,几个同学学习都非常积极。

网易公开课《单变量微积分》的课里麻省理工教授在说到链式法则的时候,拿出了一条长链,相信很多同学对此会很感兴趣。在讲到解析几何里的单叶双曲面时,我总会以广州塔为例,这也恰好是王爱玲教授所说的第五点——善于利用学生生活中的数学资源。

结语

笔者虽然已经做好了满足基本教学需求的课件,也使用了inkscape等工具制作图形形象化地解释某些知识点。但对于学习成本比较高的利用manim制作视频等需要大量的时间与熟练的技巧。暂时还只是搭建了运行环境,并未做出更多丰富的实用的教学视频。