“特殊”操作“一般”思考

文／王竞进

同学们，我们先来看小明与小亮一起做的一个“游戏”。

小明背对小亮，让小亮按下列4个步骤进行操作：

第一步：分发左、中、右三堆牌（每堆张数相同且不少于两张）；

第二步：从左边一堆拿出两张，放入中间一堆；

第三步：从右边一堆拿出一张，放入中间一堆；

第四步：左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆。

这时，小明准确说出了中间一堆牌现有的张数为5张。

小亮不服气，又按上述步骤操作一遍。小明仍然准确说出了中间一堆牌现有的张数。

一、从游戏活动的解密，整体感受代数式的价值

这其中有什么奥妙吗？其实，在第一次游戏中，我们不妨设左、中、右三堆牌的张数为m（m≥2）。然后，小亮操作第二步“从左边一堆拿出两张，放入中间一堆”，此时，左边一堆的张数为（m-2），中间一堆的张数为（m+2）；再操作第三步“从右边一堆拿出一张，放入中间一堆”，右边一堆的张数为（m-1），中间一堆的张数为（m+2+1），即（m+3）；第四步后，中间一堆牌现有的张数为（m+3）-（m-2）=5。

这个游戏不仅能让我们领悟到数学的趣味性，还能感受到数学的奥妙，体会到用字母表示数所具有的优越性和一般性。这是数学知识从小学算术到初中数学的一次质的飞跃。

二、从游戏过程的分析，整体领略代数式研究的内容

在后续的多次游戏中，我们仍然设左、中、右三堆牌的张数为m（m≥2）。若这样操作第二步，“从左边一堆拿出a张，放入中间一堆”，此时，左边一堆的张数为（m-a），中间一堆的张数为（m+a）；再操作第三步“从右边一堆拿出b张，放入中间一堆”，右边一堆的张数为（m-b），中间一堆的张数为（m+a+b）；第四步后，中间一堆牌现有的张数为（m+a+b）-（m-a）=2a+b。也就是说，小明只要知道a和b的值，就能够知道并说出中间一堆牌现有的张数。这个数值与左、中、右三堆牌原始的张数没有关系。

对游戏活动过程的分析，能够充分体现本章将要研究、探索和学习的知识。用字母m、a、b分别表示操作过程中牌的张数，实际上就是列代数式，其中m、a、b都是单项式，m+a、m-b、m+a+b以及2a+b都是多项式。将（m+a+b）-（m-a）化简为2a+b，这实际上还经历了去括号、合并同类项的过程。每次游戏所得的结果，本质上就是对a、b取不同值时代数式2a+b的值。如果你能深刻理解本章内容，也就能同小明一样，迅速地报出中间一堆牌现有的张数。同样，我们还要学会运用整式的加减解决生活中的一些实际问题。

本章知识结构图如图1所示。

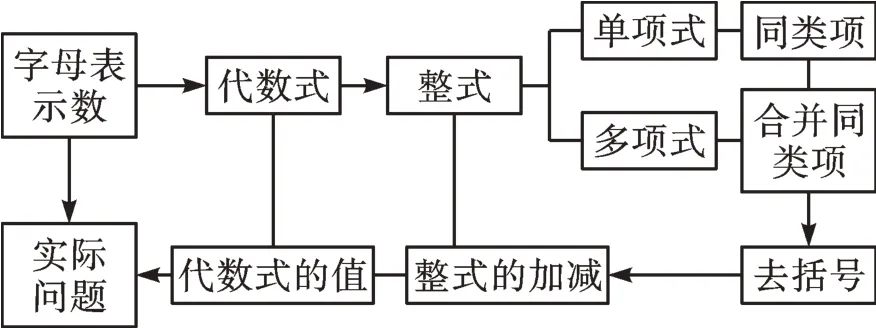
图1

在上述游戏活动的过程中，我们一起经历了数次从摆放特殊张数的操作，到一般规律的归纳发现，还领悟到“代数式”这一章所蕴含的数学思想，比如从直观到抽象、从具体到一般。希望同学们在学习过程中能细细品味这些数学思想，提高我们应用适当的模型解决实际问题的能力。