基于有限元的农用拖拉机挡泥板弯曲成形分析及优化

王 硕,吴 艳,马炎漫,曾如铁,熊锦林

基于有限元的农用拖拉机挡泥板弯曲成形分析及优化

王 硕,吴 艳*,马炎漫,曾如铁,熊锦林

武汉轻工大学机械工程学院, 湖北 武汉 430048

借助DYNAFORM有限元软件建立农用拖拉机挡泥板弯曲成形的有限元模型，分析厚度、压边力、冲压速度、摩擦系数和凹凸模间隙对其弯曲回弹的影响规律，研究6061铝合金农用拖拉机挡泥板的回弹问题。在数值模拟的基础上，通过正交优化分析得出：在一定范围内，农用拖拉机挡泥板的回弹量与厚度、压边力、冲压速度、摩擦系数呈现负相关关系，与凸凹模间隙呈现先负后正相关关系；影响回弹量的因素排列次序为压边力、凹凸模间隙、厚度、摩擦系数、冲压速度；最优参数组合为厚度2 mm，压边力300 kN，冲压速度5000 mm∙s-1，摩擦系数0.65及凹凸模间隙1.65 mm。同时，基于工艺参数优化，采用等效拉延筋和回弹补偿策略共同控制该制件的回弹，结果分析表明：等效拉延筋起到降低回弹程度的作用；回弹补偿策略能够有效地减小回弹量。本项研究表明，采用工艺参数控制法、等效拉延筋法和回弹补偿策略能够有效地控制农用拖拉机挡泥板的弯曲回弹程度，为挡泥板实际生产加工过程提供坚实的理论基础与可靠的数值依据。

农用拖拉机挡泥板;数值模拟;正交试验;回弹优化及补偿

随着汽车轻量化进程的不断推进，冲压成形工艺在汽车零件生产中得到了广泛应用。近年来，材料轻量化问题备受关注，研究表明，通过减轻汽车质量10%，可实现油耗降低6%～7%[1]。实现汽车质量减轻的主要途径之一是采用轻量化材料替代传统钢板，而铝合金因其低密度、轻重量、高比强度、高比刚度、强耐腐蚀性以及高回收率等优点，被公认为是最具研究价值的轻量化材料之一[2]。因此，铝合金在汽车轻量化技术中逐渐替代汽车钢板并得到广泛应用[3]。同时，农用拖拉机作为农业中不可或缺的设备，其挡泥板作为必要零件，其成形过程存在着起皱、破裂及回弹等问题，这些缺陷在一定程度上制约了农用拖拉机在汽车轻量化进程中的发展与推广。在这些缺陷中，回弹被认定为弯曲成形过程中最难控制的缺陷之一[4]。

汽车零件的回弹优化与补偿问题一直都是学者研究的热点。例如，艾锋[5]以某汽车挡泥板为研究对象，基于Design-exper软件建立摩擦系数、压边力、拉延筋阻力系数与板料拉裂、起皱之间关系的数学模型，以解决板料成形中起皱、破裂及回弹的问题；王大鹏[6]等人为解决某汽车纵梁冲压成形过程中存在的破裂、起皱和回弹等缺陷，采用基于正交试验设计、数值模拟、克里金模型和遗传算法相结合的优化策略，并使用DYNAFORM有限元软件对某汽车纵梁进行了工艺优化和回弹补偿；苟春梅[7]等人研究了某汽车后地板零件的回弹控制问题，采用AutoForm软件对某汽车后地板零件进行工艺优化和回弹补偿。这些研究都属于采用数值模拟技术模拟金属板料成形过程，并进行缺陷预测与改善的领域。实际研究表明，不同结构的制件成形过程存在着截然不同的变化规律，各工艺参数对于制件成形质量有着不同的影响[1]。农用拖拉机挡泥板在弯曲成形过程中容易出现回弹现象，该难题严重影响着农用拖拉机挡泥板的成形质量、尺寸精度与使用寿命等。

本文主要从优化工艺参数和改善铝合金板料弯曲性能两个角度出发，通过对6061铝合金挡泥板弯曲成形进行数值模拟，考察厚度、压边力、冲压速度、摩擦系数和凹凸模间隙等工艺参数对其弯曲回弹的影响，结合优化设计理念，从而达到改善农用拖拉机挡泥板成形质量的目的，为解决6061铝合金板料回弹提供理论基础与数值依据，这对于提高弯曲件的产品质量和生产效率具有重要意义。

1 材料及零件模型

1.1 材料参数和模型

在大多数情况下，农用拖拉机挡泥板主要采用钢材等重质材料进行制造。6061铝合金虽然不常作为生产挡泥板等关键零件的首选材料，但考虑到减轻整体重量的需求，选用其作为挡泥板材料。此外，6061铝合金具备优异的强度、耐腐蚀性和可加工性等特性，这些特性使其能够满足挡泥板在实际使用中的基本需求。采用6061铝合金作为农用拖拉机挡泥板材料，其化学成分如表1所示[8]。通过6061铝合金板料单向拉伸试验获得力学性能数据，拟合数据输入至DYNAFORM软件中的36号材料模型(3参数Barlat材料模型)。36号材料模型特别适合应用于任何金属薄板冲压成形分析中，能够更好地反映出各向异性对冲压成形的影响，从而获得更可靠的分析结果[9,10]，故6061铝合金材料须采用此模型进行分析。

表 1 6061铝合金化学成分表

在DYNAFORM软件中创建6061铝合金材料模型，其力学性能参数如表2所示，应力-应变曲线及成形极限曲线如图1所示[8]。

表 2 6061铝合金力学性能参数表

图 1 应力-应变曲线(a)及成形极限曲线(b)

1.2 成形工艺分析

本文研究的是400-12型号的农用拖拉机前轮挡泥板，该挡泥板适配时风和福田品牌的小型农用拖拉机，成形工艺为翻边-弯曲。弯曲毛坯件的尺寸计算[11]：

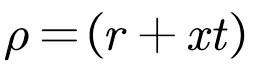
图 2 农用拖拉机挡泥板工件图

1.3 有限元模型

运用CATIA软件设计出农用拖拉机挡泥板的三维模型，并且将其进行相应处理后，导入DYNAFORM软件中进行网格划分。采用双动成形技术，利用DYNAFORM模面工程(DFE)模块，自动生成凸模、凹模和压边圈工具，并对相应的参数及成形工序进行了定义与设置。有限元分析中的网格质量是确保模拟准确性和计算效率的关键[9]。在DYNAFORM软件中，壳元网格适用于薄壁结构成形模拟，能够有效捕捉材料的厚度变化。结合自动、手动网格划分及其局部细化，允许仿真初步验证后逐步提高网格密集度，增强模拟仿真的精度，使设计验证和性能预测更为精确。在板料弯曲冲压过程中，凸模下行，压边圈与凹模首先贴合并压紧板料，凸模继续下行完成弯曲冲压。模拟过程中不考虑板料与模具之间的热交换问题，即将其视为等温问题[8]。6061铝合金农用拖拉机挡泥板弯曲成形有限元光照模型，如图3所示。

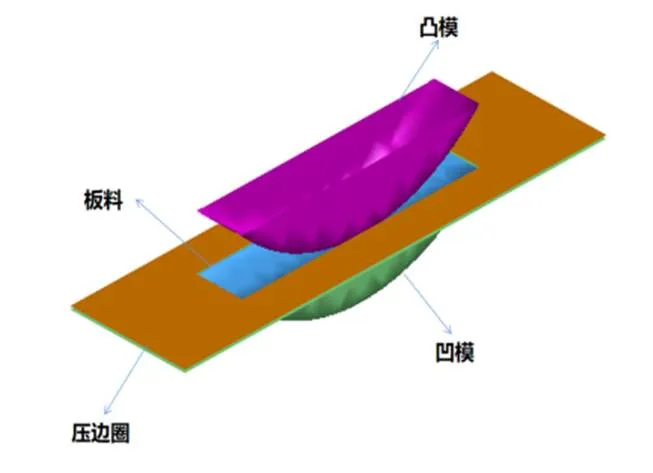
图 3 农用拖拉机挡泥板弯曲成形有限元光照模型

2 基于正交试验的回弹分析

2.1 正交试验

正交试验具有优良的均衡分散性和整齐可比性，能够简化数值模拟及计算的繁杂性，是研究多变量多水平问题的有效试验方法[12,13]。在板料弯曲成形过程中，回弹量受到很多因素的影响，但材料确定后，其他主要影响因素就是工艺参数[14,15]，例如厚度、压边力、冲压速度、摩擦系数和凹凸模间隙等。这些工艺参数对弯曲件的成形质量起着至关重要的作用。

本文正交试验考察了以上5个影响因素，其主要目的是研究各影响因素对弯曲回弹量的影响程度并探讨其影响规律。正交试验能否取得实质性效果的关键是，确定影响因素的水平[16]。在本试验中，根据板料成形数值模拟经验，可将厚度分别设定为1.0 mm、1.5 mm和2.0 mm三个水平；结合实际生产经验和文献[2]，综合考虑取100 kN、200 kN和300 kN作为压边力的三个水平[2]；在板料成形数值模拟时，通常将实际拉深速度放大若干倍作为冲压速度(即虚拟冲压速度)，依据文献[2]作为参考，故取1000 mm∙s-1、3000 mm∙s-1和5000 mm∙s-1作为冲压速度的三个水平[2]；在数值模拟中，可以认为挡泥板制件各处的摩擦系数是一致的[17]，取6061铝合金板料在1427润滑剂、3959润滑剂以及无润滑剂（干摩擦）三种润滑条件下的摩擦系数，分别为0.10、0.14和0.65，并将其设定为摩擦系数的三个水平；在实际生产过程中，通常根据经验公式=(0.9～1.3)来确定凹凸模间隙，故将凹凸模间隙设定为0.9、1.1和1.3三个水平（值指厚度大小）。

采用上述5个因素作为研究因素，针对每个因素设置3个不同的水平值，并且制定出正交试验因素水平表，具体内容详见表3。

表 3 正交试验因素水平表

基于上述因素水平表，则相应地选择18(37)标准正交试验表，正交表中会有2个空白列，且在试验中不起作用，但可以用于其他分析。回弹问题是直接影响农用拖拉机挡泥板成形质量的最大问题，需要对回弹量(弯曲角回弹量)进行综合性研究，故将其设置为评价指标。在板料弯曲成形数值模拟过程中，根据公式(4)[2]能够计算出弯曲变形区在卸载过程中的弯曲角回弹量大小。

(4)

式中[2]：0—加载时的中性层曲率半径；0—加载时的弯曲角；´0—卸载后的中性层曲率半径；∆—卸载后的弯曲角回弹量。正交试验表列于表4。

表 4 正交试验表

2.2 极差与方差分析

极差分析结果如表5所示，从此表中可以看出厚度、压边力、冲压速度、摩擦系数和凹凸模间隙5个因素均为有效影响因素。从极差分析结果来看，因素的极差值愈大，则说明回弹量受到该因素的影响愈显著。由表5可知，影响回弹量的因素排列次序为(压边力)>(凹凸模间隙)>(厚度)>(摩擦系数)>(冲压速度)。

回弹量越小，即各因素水平对应的k值也越小[7]。因素3较小，故3较好；因素3较小，故3较好；因素3较小，故3较好；因素3较小，故3较好；因素2较小，故2较好。根据各因素水平的值，得到最优参数组合为33332，即厚度为2.0 mm，压边力为300 kN，冲压速度为5000 mm∙s-1，摩擦系数为0.65及凹凸模间隙为1.65 mm。

表 5 极差分析结果

注: 其中k为同一因素下第个水平的回弹量平均值(=1、2、3)，为因素的极差。

Note: In this context,krepresents the average rebound quantity at theth level under the same factor (=1,2,3), anddenotes the range of the factor.

由于极差分析无法估计试验误差的大小，也不能进行显著性测量[18]。通过方差分析，可进一步了解各因素对回弹量影响的量化估计[19]。根据各因素的试验数据进行定量分析，得出各因素的显著性结果。各因素对回弹量影响的方差分析结果，如表6所示。

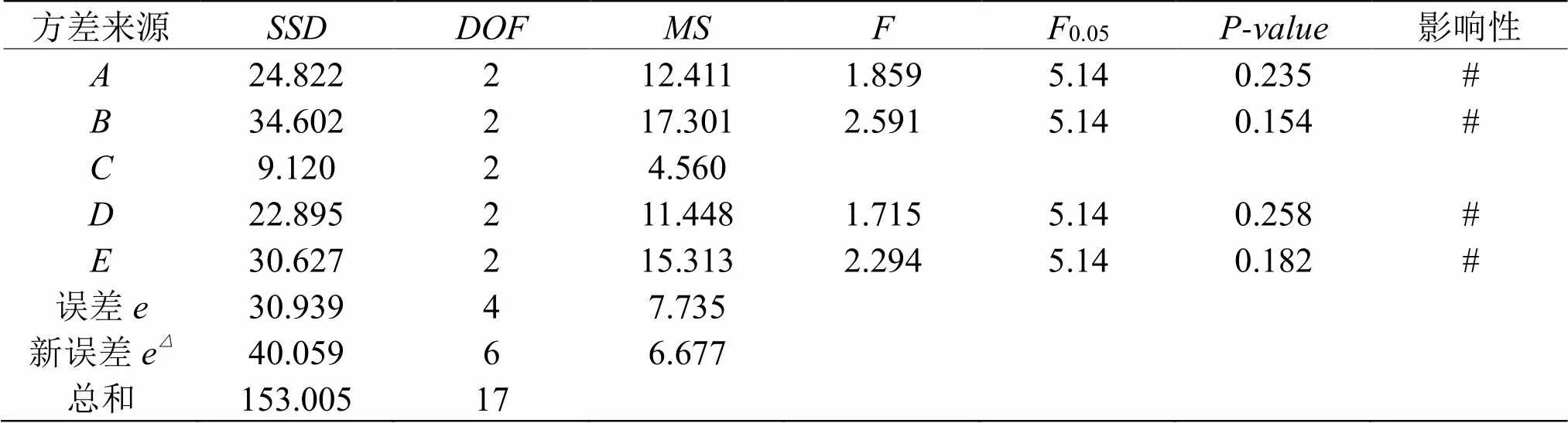
表 6 方差分析结果

注:1.离差平方和；自由度；-均方；-分布统计量；0.05-显著性水平=0.05时查表获得的临界值，0.05=5.14；因素对试验结果无显著影响的概率；-该因素的影响性显著；-该因素对试验结果有影响，但不显著。

2.均方计算完成后，若某个因素的均方比误差的均方小或者相等，则应该将这些因素归为误差[5]，从而构成一个新误差e。在方差分析中得到MS＜MS，这表明了因素对试验结果的影响较小，将其归入误差，从而形成新误差e，新误差e的离差平方和、自由度和均方都发生变化。

Note: 1.-Sum of Squares for Deviation;-Degrees of Freedom;-Mean Square;-distribution statistic;0.05-the critical-value at the significance level=0.05, where0.05=5.14;-value-the probability that the factor has no significant impact on the experimental results;-indicates that the effect of the factor is significant;-indicates that the factor has an effect on the experimental results, but it is not significant.

2. After calculating the mean square, if the mean square of a factor is less than or equal to that of the error, these factors should be attributed to the error[11], thus forming a new errore. In the analysis of variance, ifMS<MS, it indicates that the influence of factoron the experimental results is minor, and it should be included in the error, forming a new errore. The sum of squares for deviation, degrees of freedom, and mean square for the new erroreall undergo changes.

方差分析结果显示，虽然各因素的值均小于0.05，但是压边力依旧是影响最大的因素，其次是凹凸模间隙、厚度以及摩擦系数，冲压速度的离差平方和很小，其影响可以忽略不计。

综合考虑极差与方差分析结果，故6061铝合金板料弯曲成形时应着重考虑压边力和凹凸模间隙的合理取值，这样容易获得回弹量较小的制件，提高制件的成形质量和生产效率。

2.3 正交试验结果分析

根据极差分析结果，绘制出各研究因素与回弹量的关系图，以便从图形上直接看出回弹量随各研究因素水平变化的大体关系。其中，横坐标为各研究因素的水平值，纵坐标为回弹量，各因素水平趋势图分别如图4、图5、图6、图7及图8所示。

6061铝合金板料弯曲成形时，其厚度会对板料的弯曲回弹量产生影响，图4中曲线表示厚度水平变化对回弹量的影响。

图 4 厚度水平趋势图

板料的厚度越大，其所承受的弯曲应力也越大，其能量分布在板料的纵深方向上也越均匀[13]。当该制件板料厚度增大时，其所承受的弯曲应力也相应增大，且位于靠近板料表面的塑性变形层的尺寸也会增加，使得板料所承受的弯曲应变分布更加均匀，进而减小回弹量。因此，在一定范围内板料厚度越大，其弯曲回弹量越小。但是，若板料厚度过大，则会产生更大的弯曲应力，可能导致板料断裂或过度变形。因此，在实际生产过程中，应根据具体要求选择合适厚度的板料弯曲成形。

压边力作为板料弯曲成形中的重要工艺参数之一，其大小能够控制材料在板料内部的流动，并且能够改善其内部应力的分布状况[20]。图5中曲线表示压边力水平变化对回弹量的影响。

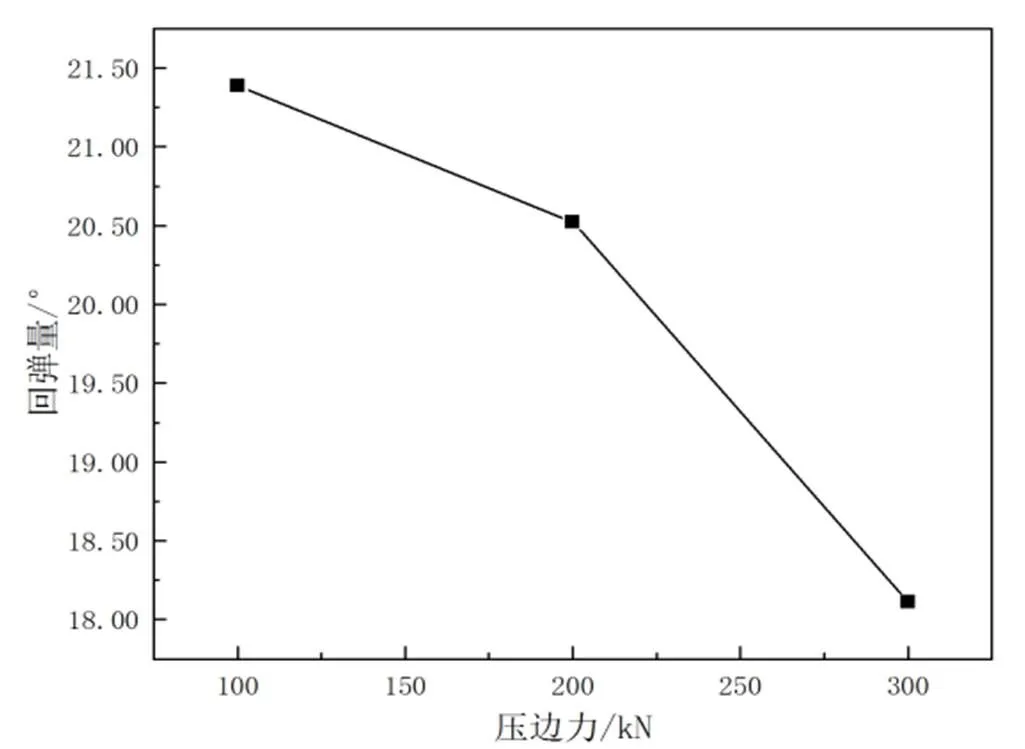
图 5 压边力水平趋势图

压边力越大，板料在弯曲处的应变越均匀，从而减小回弹量。因此，在一定范围内压边力越大，回弹量越小。总体来说，如果合理地控制压边力大小，则能够最大程度地减小回弹程度，从而保证制件成形质量。

冲压速度的快慢会影响板料的形变速率和形变历程[21]，进而影响回弹量，图6中曲线表示冲压速度水平变化对回弹量的影响。

图 6 冲压速度水平趋势图

从图6中的曲线可以看出，虽然回弹量随着冲压速度增加而减小，由于冲压速度对回弹量的影响较小，故回弹量的变化范围也较小。因此，在一定范围内冲压速度越大，回弹量越小。

在板料弯曲成形过程中，摩擦系数能够影响板料的形变过程、能量分布和形变均匀性[10]，从而影响回弹量。图7中曲线表示摩擦系数水平变化对回弹量的影响。

图 7 摩擦系数水平趋势图

从实质上分析，板料弯曲成形时两侧边缘部分发生折弯变形，而中间部分则发生拉伸变形，当摩擦系数较小，则凹凸模表面与板料表面间的摩擦力较小，板料形变时可能会出现滑动和相对错位的情况，从而增加板料的弯曲不一致性，进而造成回弹量增加。板料发生塑性变形时，摩擦系数愈大，变形抗力愈大。随着摩擦系数的增大，板料变形区的内外层所承受的压拉应力状态呈现出一致的趋势，导致回弹量的减少。因此，在一定范围内摩擦系数越大，回弹量越小。在板料弯曲成形过程中，需要合理控制摩擦系数大小，通过涂抹润滑剂以及调整模具表面的处理方式、材质等方法，以减小回弹量，从而保证制件成形质量。

凹凸模间隙水平变化对回弹量的影响，如图8中曲线所示。

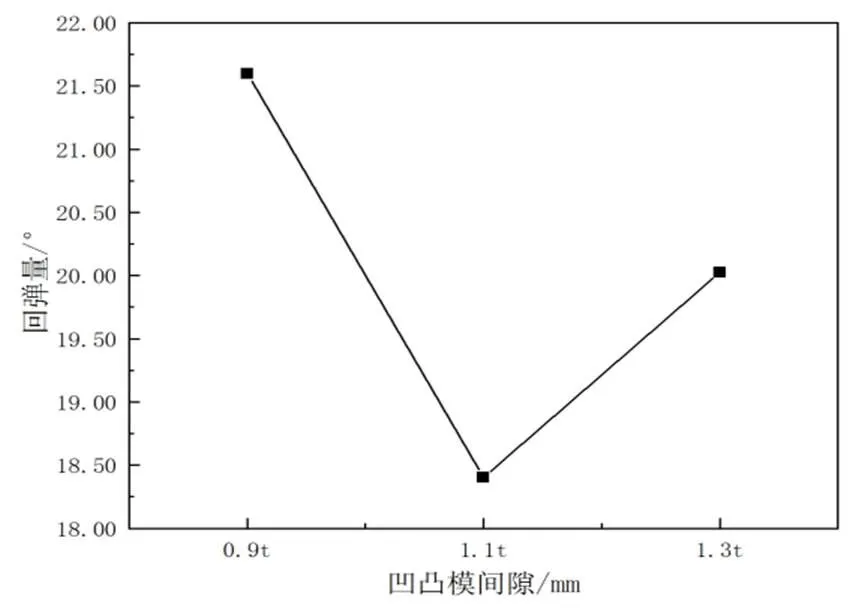
图 8 凹凸模间隙水平趋势图

从图8中的曲线可以看出，随着凹凸模间隙的增加，回弹量大小呈现出先下降后上升的趋势，故应该合理地选择凹凸模间隙，既不能太大，也不能太小，要使得板料塑性能力充分发挥，尽量得到最佳的弯曲回弹量。若凹凸模间隙较大，则板料受力分布不均，增加板料变形难度，会导致弯曲回弹量增大。同时，凹凸模间隙较大，还会容易导致板料发生材料堆积，出现起皱现象。反之，若凹凸模间隙较小，则在板料形变时难以应对应变的压力，引起塑性发挥不够，从而造成弯曲不均匀、变形不一致的问题，导致弯曲回弹量增加。

3 回弹优化及补偿

3.1 最优组合的数值模拟

通过基于正交试验的回弹分析得到最优参数组合33332，将其进行数值模拟验证，得到回弹模型，如图9所示。

图 9 回弹模型图

3.2 回弹优化

采用等效拉延筋方法，对最优参数组合的回弹模型进行优化，观察是否能够得到回弹效果更好的模型。等效拉延筋布局，如图10所示。采用等效拉延筋的回弹模型，如图11所示。

图 10 等效拉延筋布局图

图 11 采用等效拉延筋方法的回弹模型图

3.3 回弹补偿

虽然采用工艺参数控制法和等效拉延筋方法降低了零件的回弹程度，但是不能完全控制零件的回弹量[7]。因此，采用回弹补偿策略对加入等效拉延筋的回弹模型进一步控制回弹。补偿后的回弹模型图12所示。

图 12 补偿后的回弹模型

4 模拟研究的结果验证

根据文献[2]中的结论表明，在一定范围内，农用拖拉机挡泥板的弯曲回弹量与厚度、压边力、冲压速度、摩擦系数呈现负相关关系，与凸凹模间隙呈现先负后正相关关系，符合6061铝合金板料的冲压成形规律。

通过一些关于DYNAFORM模拟研究(Jstamp/NV)的验证结果表明[23,24]，适当地采用工艺参数控制法、等效拉延筋法、回弹补偿策略能够降低回弹程度，解决回弹问题，这也与实际生产中的经验规律相符合。

由于本文研究的零件与参考文献中的零件存在差异，因此参考文献中的结果与本文的结论可能存在些许差异。例如，针对冲压速度因素，本文只得出“随着冲压速度增加，回弹量减小”的结论，但未得到“回弹较大的区域面积增加”现象。这种差异可能是由于不同零件的几何形状、材料特性或模拟参数等因素引起的。目前的研究正在积极解决这些验证问题，也在进行物理试验，以确保结果的可靠性和一致性。这一系统的努力有助于提升对回弹行为的全面理解，为未来的研究和应用提供更为可靠的基础。

5 结 论

（1）基于有限元仿真分析，构建了农用拖拉机挡泥板及其模具有限元模型。同时，采用正交试验研究了厚度、压边力、冲压速度、摩擦系数和凹凸模间隙5个影响因素对制件弯曲回弹的影响。根据极差与方差分析，得出影响回弹量的因素主次顺序为：压边力>凹凸模间隙>厚度>摩擦系数>冲压速度，并且得到了最优参数组合33332，即厚度为2.0 mm，压边力为300 kN，冲压速度为5000 mm∙s-1，摩擦系数为0.65及凹凸模间隙为1.65 mm；

（2）根据正交试验和各因素水平变化趋势图，分析得出：在一定范围内，农用拖拉机挡泥板的弯曲回弹量与厚度、压边力、冲压速度、摩擦系数呈现负相关关系，与凸凹模间隙呈现先负后正相关关系；

（3）在最优参数组合的回弹模型上，采用等效拉延筋方法对6061铝合金板料弯曲成形进一步优化，以达到改变进料阻力分布、调节材料流动情况的目的，从而减小回弹量。同时，也验证了拉延筋模型能够有效地降低回弹程度；

（4）在使用等效拉延筋的回弹模型基础上，采用回弹补偿策略对制件进行回弹补偿，其回弹量明显减少；

（5）本项研究表明，采用工艺参数控制法、等效拉延筋法和回弹补偿策略能够有效地控制制件的回弹问题，缩短试模调试时间，降低模具成本。

致谢:感谢湖北省教育厅科学研究计划，编号：D20221606资助。

[1] 臧其其,闫华军,张双杰,等.基于Dynaform的铝合金汽车地板梁成形分析及工艺参数优化[J].塑性工程学报,2019,26(2):125-131

[2] 任静.6061铝合金板材冲压成形回弹问题研究[D].武汉:华中科技大学,2017

[3] 张铧.铝合金变压边力冲压成形的模拟分析及智能预测[D].合肥:合肥工业大学,2010

[4] 柴海啸,胡树根,王耘.基于神经网络的板料冲压回弹预测系统的研究[J].机械工程师,2006,24(1):82-84

[5] 艾锋.基于Design-expert软件的汽车挡泥板多目标优化[J].热加工工艺,2015,44(11):126-131

[6] 王大鹏,李晓峰.某汽车内板冲压成形工艺优化及回弹补偿[J].塑性工程学报,2022,29(9):40-46

[7] 苟春梅,吴民,董静,等.汽车冲压件工艺参数优化及回弹控制[J].锻压技术,2018,43(2):34-37

[8] Ma WP, Wang BY, Xiao WC,.Springback analysis of 6016 aluminum alloy sheet in hot V-shape stamping [J]. Journal of Central South University, 2019,26(3):524-535

[9] 李奇涵,王文广,邓义,等.基于数值模拟的油箱底壳拉延筋设置与优化[J].锻压技术,2014,39(12): 31-34

[10] 尹晓阳,凃杰松,段海涛,等.表面润滑对6061铝合金板材成形性能的影响[J].塑性工程学报,2018,25(2):65-72

[11] 王孝培.冲压手册[M].2版.北京:机械工业出版社,2011:178

[12] 郜晓,刘妮娜,李俊,等.加强黄土的动力特性研究[J].地震工程学报,2022,44(4):854-864

[13] 王苏静,邓沛然,宣守强.6061高强度铝合金拉深工艺参数优化[J].模具工业,2021,47(2):6-10

[14] 郭驿.拉延筋对拉深成形及回弹影响的关键技术研究[D].合肥:合肥工业大学,2017

[15] 高嵩,于长春,梁继才,等.铝型材多点三维拉压复合弯曲成形工艺[J].机械工程学报,2019,55(20):152-159

[16] 车利,李小曼,王悉颖,等.6061铝合金飞机溢油口拉深成形研究[J].精密成形工程,2023,15(3):112-119

[17] 余国庆,鲁世红.基于有限元分析的铝合金板料弯曲回弹的影响因素研究[J].机械科学与技术,2005(9):1077-1080

[18] 闵范磊,朱光明,高绪杰,等.铝合金板材挤压自弯曲成形机理及模具优化设计[J].中国有色金属学报,2021,31(12):3508-3519

[19] 沈智,金康,周英丽,等.6014铝合金U形件弯曲回弹[J].锻压技术,2021,46(10):88-92

[20] Zhou J, Yang XM, Wang BY,. Springback prediction of 7075 aluminum alloy V-shaped parts in cold and hot stamping [J]. The International Journal of Advanced Manufacturing Technology, 2021,119(1-2):203-216

[21] Sun XM, Ji YN, Xiao A,Influence of single-pulse and high-amplitude current on springback and mechanical properties of AA5052 aluminum alloy sheets [J]. Materials Characterization, 2022,194:167-185

[22] 刘迪辉,李光耀.等效拉延筋模型对回弹预测的影响[J].塑性工程学报,2007,67(6):88-91

[23] 张泉达,孙福臻,吉日格勒,等.基于Dynaform的球底筒形件充液成形回弹有限元模拟[J].锻压技术,2023,48(5):275-281

[24] 张勇,范轶,薛洋.基于DYNAFORM和正交试验的轿车加强梁冲压工艺参数优化[J].锻压技术,2019,44(2):37-42

Finite Element-based Analysis and Optimization of Agricultural Tractor Fender Bending

WANG Shuo, WU Yan*, MA Yan-man, ZENG Ru-tie, XIONG Jin-lin

430048,

With the help of Dynaform finite element software to establish the finite element model of agricultural tractor fender bending and forming, we analyzed the thickness, crimping force, stamping speed, friction coefficient and concave and convex mode gap, and studied the resilience of 6061 aluminum alloy agricultural tractor fender. On the basis of numerical simulation, through orthogonal optimization analysis, it is concluded that, within a certain range, the rebound quantity ofagricultural tractor fender is negatively correlated with the thickness, crimping force, stamping speed and friction coefficient, and negatively correlated with the concave-convex mold gap; the factors affecting the rebound quantity are in the order of crimping force, concave-convex mold gap, thickness, friction coefficient, stamping speed, the optimal parameter combination of the thickness of 2 mm, crimping force of 300 kN, concave-convex mold gap, friction coefficient, stamping speed. The optimal parameter combination is thickness of 2 mm, crimping force of 300 kN, stamping speed of 5000 mm•s-1, friction coefficient of 0.65 and die clearance of 1.65 mm. Meanwhile, based on the optimization of process parameters, the rebound of the part is controlled by the equivalent stretching bar and the rebound compensation strategy, the results shows that: the equivalent stretching bar plays a role in reducing the degree of rebound; the rebound compensation strategy can effectively reduce the amount of rebound. This study shows that the process parameter control method, the equivalent stretching bar method and the rebound compensation strategy can effectively control the degree of bending rebound of the agricultural tractor fender, and provide a solid theoretical basis and a reliable numerical basis for the actual production process of the fender plate.

Agricultural tractor fender; numerical simulation; orthogonal testing; rebound optimization and compensation

TG389

A

1000-2324(2023)05-0782-10

10.3969/j.issn.1000-2324.2023.05.019

2023-10-27

2023-11-11

混晶调控改善再结晶纳米变形镁合金热稳定性机制模型研究(D20221606)

王硕(2000-),男,硕士研究生,主要研究方向:金属材料冲压成形工艺.E-mail:ws17860245596@163.com

Author for correspondence. E-mail:wuy611@163.com