改进深度神经网络的用户用电量预测方法

蔡翔 朱莉

[摘 要]针对深度神经网络对电能预测精度低的问题，提出正弦粒子群优化神经元数量的深度神经网络算法，通过对粒子群算法进行变异操作和惯性权重改进，来对深度神经网络隐藏层神经元参数进行寻优。实验结果表明，SPSONN-DNN算法相比于DNN、极度梯度提升、线性回归、两种改进PSONN-DNN算法的预测精度分别提高了1.926%、2.820%、1.500%、0.633%、0.582%；SPSONN-DNN算法相比于两种改进PSONN-DNN算法迭代次数分别减少6次、4次。

[关键词]电量预测；深度神经网络；粒子群算法；预测精度

[中图分类号]TP391[文献标识码]A

电量预测是智能电网中电能调度的理论依据，提前通过预测模型来推测出各地区的用电量，使供电部门的输电量和各地区的用电量达到供需平衡，从而减少电网中电能的浪费^[1]。随着人工智能的兴起，深度神经网络由于具有自学习、自适应、容错性等特点，大量的学者将其应用在电量预测领域，但是深度神经网络处理不同领域的数据集时，由于数据的多样性导致深度神经网络的结构参数不同。人们利用其它算法的优点来对深度神经网络的结构参数进行优化，但只是对神经网络中的训练数据、学习率、输入权值等参数进行寻优，而隐藏层神经元数量是根据输入参数随机设置的，不是最佳的參数，导致网络的模型达不到最优，模型预测精度较低^[2-3]。

优化算法能准确的对深度神经网络各隐藏层神经元进行寻优，其典型方法有粒子群算法、遗传算法、蚁群算法。又因粒子群算法相比于遗传算法、蚁群算法需要调整的参数少、搜索速度快、效率高以及简单容易实现等优点^[4-5]。本文利用改进粒子群算法来优化深度神经网络各隐藏层神经元数量。

1 算法设计

1.1 SPSONN-DNN预测模型框架

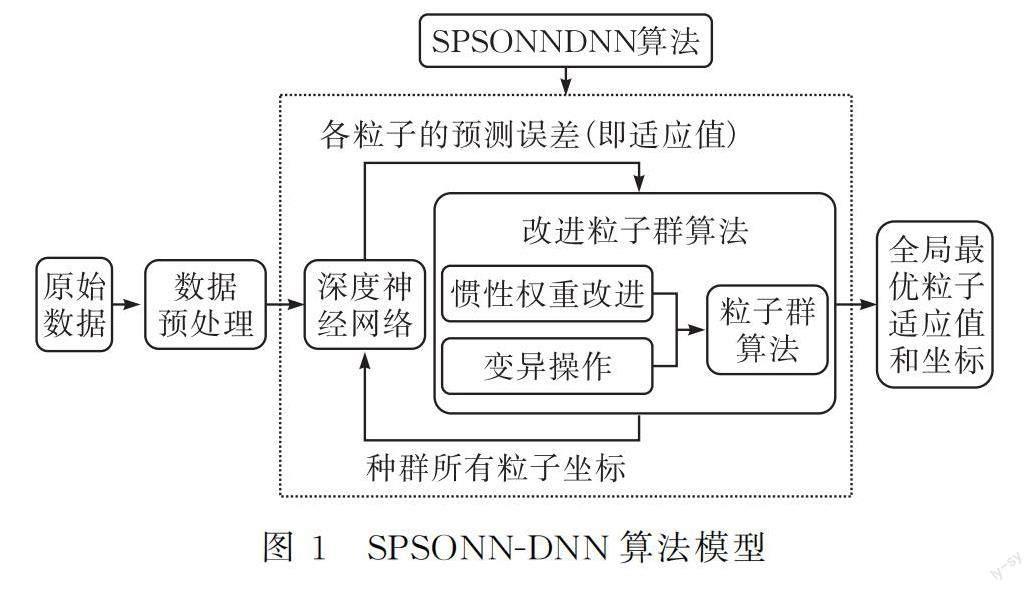
改进粒子群优化深度神经网络的模型见图1。

本文原始数据为某地区的家庭用电量数据，数据包括日期、时间、平均有功功率、平均无功功率、平均电压、平均电流、3个计量表等9个维度的参数。

首先，对原始数据进行预处理。在数据预处理过程中，先将数据格式进行转换，然后将数据的日期和时间转换为浮点型，将各参数的单位换算统一；接着查找缺失、异常字符串的数据并将其删除，因为是对家庭用电量进行短期预测，删除对数据的整体没有影响。

SPSONN-DNN算法是利用改进粒子群算法的种群粒子在迭代过程中的位置坐标来确定深度神经网络隐藏层神经元数量，深度神经网络根据每个粒子坐标来确定其对应的预测误差（即适应值），粒子群算法从所有粒子中寻找出最优粒子，然后再根据粒子群的速度和位置更新公式来更新所有粒子，经过多次迭代后寻找出全局最优粒子，全局最优粒子坐标和适应值分别代表深度神经网络隐藏层神经元的数量和相对应的预测误差^[6]。

1.2 粒子群惯性权重的改进

粒子群算法是通过模拟鸟群觅食的行为而发展起来的一种基于群体协作的随机搜索算法^[7-8]。

粒子群有两个特性：速度和位置。速度大小决定下一次迭代后的位置变化大小；位置的维度是由所要解决的问题决定的，每个粒子的位置信息可以看成适应函数的一组解，每个粒子空间坐标的不断变化，代表其函数解也是在不断变化的。PSO算法中粒子的速度和位置公式如下：

式中，v^k_id表示粒子i第k次迭代的飞行速度的第d维分量；x^k_id表示粒子i第k次迭代的位置矢量的第d维分量；pbest_id表示粒子i第d维分量的局部（即个体）最优值；gbest_id表示粒子i第d维分量的全局（即群体）最优值；c₁、c₂表示学习因子；r₁、r₂表示取值范围在[0，1]之间的随机数；w表示惯性权重（非负数）。

通过对粒子群算法的分析可知，粒子群算法的搜索能力和收敛能力都与惯性权重w息息相关。根据分析，粒子群算法在寻优时，前期需要速度较大，从而提高全局搜索能力；中期需要速度适中，来平衡全局搜索能力和局部搜索能力；后期需要速度较小，使得局部搜索能力较强。

惯性权重为固定值已经很难满足粒子群算法在寻优过程中全局搜索能力和局部搜索能力的转换。很多学者提出了优化的方法，一般分为线性和非线性两种方法：

式中，w是指惯性权重，w_max、w_min分别代表最大、最小惯性权重值，t_max表示种群的最大迭代次数，t表示种群的当前迭代次数。

公式（3）是线性变换，在粒子群算法迭代过程中惯性权重变化率相同，不能满足粒子群算法在迭代前期惯性权重变化较小的要求；公式（4）是非线性变换，在粒子群算法迭代中期，变化仍然很小，不能很好平衡全局搜索能力和局部搜索能力。

为了使粒子群算法计算结果更加准确，提出了正弦惯性权重，使惯性权重随着粒子的迭代次数而成正弦变换，满足粒子群算法在整个迭代过程中全局搜索能力和局部搜索能力的转换如下式：

式中，w表示惯性权重，w_max、w_min分别表示惯性权重的最大值和最小值，iter表示当前迭代次数，iter_max表示最大迭代次数。

1.3 粒子群陷入局部最优的改进

粒子群虽然对惯性权重进行了改进，但是在寻优的过程中，随着种群聚合程度越来越高，种群也可能会汇聚于一点。发生这种情况的根本原因是种群在迭代寻优的过程中，其本身的多样性逐渐降低，导致陷入局部最优。为了解决这个问题，引入种群平均距离来描述种群的离散程度，根据平均距离的大小和迭代误差来判断种群是否陷入局部最优。

式中，L（iter）表示种群在第iter次迭代的平均距离，N表示种群的粒子数，d表示粒子的维度，x_in（iter）表示第i个粒子的n维分量在iter次迭代的值，x-_n（iter）表示所有粒子在iter次迭代的平均坐标的n维分量的值。

当种群粒子平均距离L（iter）的值较大时，粒子分布程度较分散，PSO进行大范围的全局搜索。随着迭代的进行，L（iter）的值会逐渐减小，表示种群中粒子分布程度较密集，种群的多样性也会降低，此时PSO易陷入局部最优，从而无法达到全局最优。

此时就需要变异操作来提高种群粒子的多样性。给定阈值，如果种群粒子平均距离L（iter）的值低于设定阈值则表示PSO陷入局部最优，应启动变异操作，将特定的粒子通过变异的方式增加种群活性，使其跳入到其它区域继续寻优，让种群达到全局最优。

可通过L（iter）的大小或粒子群全局最优值来判断是否需要进行变异操作。若粒子经过多次迭代仍未发生明显变化或A低于给定的阈值，则可进行变异操作。变异操作时根据粒子离全局最优的距离来选取变异操作的粒子，而变异前后粒子群的最优值保持不变。变异操作的公式如下：

式中，x′_i表示粒子i变异后的位置，x_i表示粒子i變异前的位置，iter是种群的当前迭代次数，iter_max是种群的最大迭代次数，N（0，1）表示0～1之间的任选随机数。

1.4 算法流程

SPSONN-DNN算法流程如下：

1）初始化。对改进粒子群算法和深度神经网络进行初始化设置，改进粒子群算法需要设置以下参数：粒子的数量N、粒子的维度D、算法的最大迭代次数iter_max、惯性权重的最大值w_max和最小值w_min以及两个学习因子c₁和c₂；深度神经网络需要设置迭代次数、隐藏层数等。

2）选取合适适应函数并计算适应值。根据具体问题，设计相关的函数关系，然后将粒子的信息输入到函数关系中求出函数的输出值（即适应值）。本文以深度神经网络损失函数为参考，以均方根误差公式作为适应度函数。

3）将初始的粒子位置参数作为DNN网络各隐藏层的神经元个数，计算出预测误差作为粒子群算法的适应值。各粒子的适应度值就是个体最优值，在个体最优值中寻找全局最优值。

4）惯性权重的更新。将种群当前迭代次数带入式（5）中，计算出新的惯性权重值。

5）更新种群各粒子的速度和位置。根据式（1）、式（2）来更新每个粒子的速度和位置。

6）将更新后的各粒子分别带入适应函数，计算出对应的适应值。

7）更新个体最优值。计算出各粒子适应值后，分别与各粒子的当前个体最优值作比较，若小于当前个体最优值，则将该粒子的适应值作为个体最优值，反之，个体最优值不变。

8）更新全局最优值。当个体最优值更新后，将各粒子的个体最优值依次与全局最优值作比较，若粒子个体最优值小于全局最优值，则将该粒子的个体最优值作为全局最优值，反之，全局最优值不变。

9）变异判断。按照公式（6）计算得到的平均距离来判断是否达到变异条件，如果距离低于给定的阈值或种群迭代多次全局最优值没有发生明显变化则执行步骤10）；否则执行步骤11）。

10）变异操作。选取部分平均距离较小的粒子，根据式（7）计算出变异后粒子位置。

11）结束循环判断。当迭代次数或者最优适应值满足种群要求后，则执行步骤12），否则执行步骤4）。

12）算法结束。输出算法计算的最优值。

SPSONN-DNN算法流程如图2所示。

2 算例分析

为验证预测方法的有效性，选用网上公布的某一地区的用户电量数据集。数据集包含平均有功功率、平均无功功率、平均电压、平均电流等数据参数。

2.1 实例分析

选取用户的用电量数据（表1），进行数据分析、过滤。首先将数据的格式统一，单位换算成统一的标准；然后查找缺失、异常字符串的数据，接着剔除异常数据或填补缺失数据；最后将处理好的数据集作为DNN、SPSONN-DNN等算法的数据集，以有功功率为输出，其它参数为输入。

2.2 实验参数设置

由式（2）、式（6）可知，需要初始化设置的实验参数有粒子的数量N、粒子的维度D、算法的最大迭代次数iter_max、惯性权重的最大值w_max和最小值w_min以及两个学习因子c₁和c₂。本文将N设置为50、D设置为6、iter_max设置为30，w_max设置为0.9、w_min设置为0.4、c₁和c₂都设置为0.2；深度神经网络隐藏层数设为6，各隐藏层神经元的数量根据全局最优粒子坐标值来确定。

2.3 实验结果与分析

深度神经网络、线性回归、极限梯度提升、两种改进 PSONN-DNN算法以及SPSONN-DNN算法分别以处理好的数据集来训练和预测用户用电量，预测结果见图3-9，本文以MAPE和MSE为标准对算法的精度进行衡量。

图3为深度神经网络的真实值与预测值误差曲线，其中蓝色曲线代表真实数据集，红色曲线表示预测数据集，MAPE为5.997%，说明训练数据集的预测值与真实值之间的平均绝对百分比误差为5.997%；MSE为0.3673，说明训练数据集的预测值与真实值之间的均方误差为0.3673。

图4表示线性回归的真实值与预测值的对比曲线图，图中横坐标表示样本点的个数，纵坐标表示每个样本点的数值，其中蓝色曲线代表真实数据，红色曲线表示预测数据。计算可知，MAPE为6.871%，即训练数据集的预测值与真实值之间的平均绝对百分比误差为6.871%；MSE为0.5717，即训练数据集的预测值与真实值之间的均方误差为0.5717。

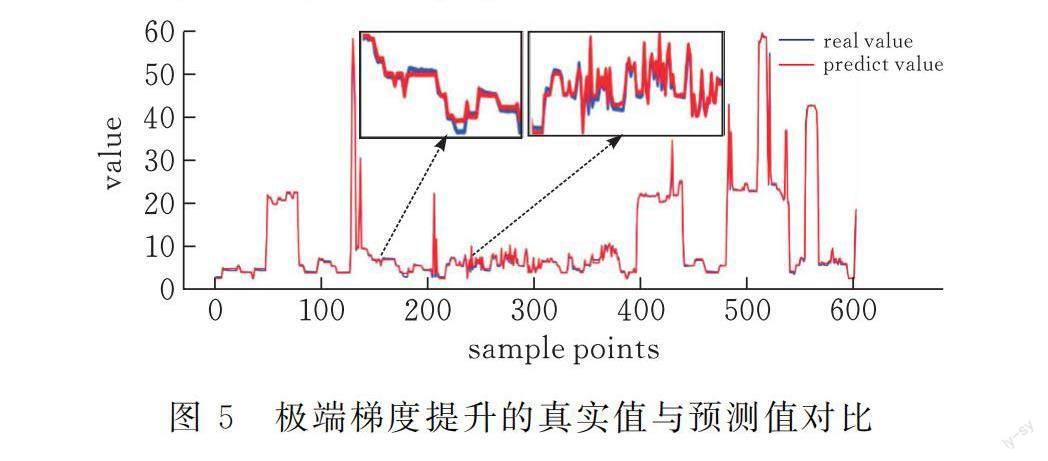
图5表示极端梯度提升的真实值与预测值对比曲线图，图中横坐标表示样本点的个数，纵坐标表示每个样本点的数值，其中蓝色曲线代表真实数据，红色曲线表示预测数据。计算可知，MAPE为5.551%，说明测试数据集的预测值与真实值之间的平均绝对百分比误差为5.551%；MSE为0.3232，说明训练数据集的预测值与真实值之间的均方误差为0.3232。

本文对粒子群优化神经元数量的深度神经网络算法中的惯性权重分别做线性变换、微分变换、正弦变换，如式（3）、（4）、（5）所示。图6中PSONN-DNN（method1）表示惯性权重为线性变换；PSONN-DNN（method2）表示惯性权重为微分变换；SPSONN-DNN表示惯性权重为正弦变换。

图6a没有设置粒子群算法的适应值阈值，可知PSONN-DNN（method1）算法的适应值（即MAPE）为4.693%，是指PSONN-DNN（method1）算法的全局最优粒子的适应值为4.693%，全局最优粒子位置为（30，15，55，27，27，13）；PSONN-DNN（method2）算法的适应值为4.622%，是指PSONN-DNN（method2）算法的全局最优粒子的适应值为4.622%，全局最优粒子位置为（54，51，45，29，3，44）；SPSONN-DNN算法适应值为4.103%，是指SPSONN-DNN算法的全局最优粒子的适应值为4.103%，全局最优粒子位置为（58，15，54，34，53，33）。因此，相比于其它两种算法，SPSONN-DNN算法预测精度有所提升。

图6b设置粒子群算法的适应值为4.9%，PSONN-DNN（method1）算法在迭代13次后达到4.9%；PSONN-DNN（method2）算法在迭代11次后达到4.9%；SPSONN-DNN算法在迭代7次时适应值达到了4.9%。因此，相比于其他两种算法，SPSONN-DNN算法迭代次数均减少了。

将PSONN-DNN（method1）算法、PSONN-DNN（method2）算法以及SPSONN-DNN算法的全局最优粒子坐标带入深度神经网络中检验其准确性。

图7表示PSONN-DNN（method1）算法的迭代次数与训练误差曲线图，图中横坐标表示样本点的个数，纵坐标表示每个样本点的数值，其中蓝色曲线代表真实数据，红色曲线表示预测数据。计算可知，MAPE为4.684%，即PSONN-DNN（method1）算法中训练数据集的预测值与真实值之间的平均绝对百分比误差为4.684%；MSE为0.2853，表示PSONN-DNN（mothed1）算法中测试数据集的预测值与真实值之间的均方误差为0.2853。

图8表示PSONN-DNN（method2）算法的迭代次数与误差曲线图，图中横坐标表示样本点的个数，纵坐标表示每个样本点的数值，其中蓝色曲线代表真实数据，红色曲线表示预测数据。计算可知，MAPE为4.633%，表示PSONN-DNN（method2）算法中訓练数据集的预测值与真实值之间的平均绝对百分比误差为4.633%；MSE为0.2846，表示PSONN-DNN（method2）算法中测试数据集的预测值与真实值之间的均方误差为0.2846。

图9表示SPSONN-DNN算法的迭代次数与误差曲线，图中横坐标表示样本点的个数，纵坐标表示每个样本点的数值，其中蓝色曲线代表真实数据，红色曲线表示预测数据。计算可知，MAPE为4.051%，表示SPSONN-DNN算法中训练数据集的预测值与真实值之间的平均绝对百分比误差为4.051%；MSE为0.2647，表示SPSONN-DNN算法中测试数据集的预测值与真实值之间的均方误差为0.2647。

综上所述，验证了PSONN-DNN（method1）算法、PSONN-DNN（method2）算法以及SPSONN-DNN算法的准确性。

由表2、表3可知，SPSONN-DNN算法的预测精度（MAPE）相比于DNN、线性回归、极限梯度提升分别提升了1.926%、2.820%、1.500%；并且SPSONN-DNN算法相比于PSONN-DNN（mothed1）算法、PSONN-DNN（mothed2）算法预测精度（MAPE）分别提升了0.633%、0.582%，迭代次数分别减少了6次、4次。实验证明，相比于传统的方法，SPSONN-DNN算法在用户电量预测中预测精度更高。本文方法在电量预测中具有普遍的适用性。

3 结论

目前，深度神经网络应用广泛，但是面对不同领域的数据集，深度神经网络隐藏层神经元参数不确定。针对这一问题，提出改进粒子群优化神经元数量的深度神经网络算法对家庭用电进行预测，该算法是将粒子群中的惯性权重改进为随迭代次数变化而成正弦变化的变量；同时在计算中加入了变异操作，使陷入局部最优的粒子跳入其它区域继续寻优。通过实验验证，SPSONN-DNN算法相比于DNN、线性回归、极限梯度提升方法的预测精度（MAPE）分别提升了1.926%、2.820%、1.500%，同时相比于PSONN-DNN（mothed1）算法、PSONN-DNN（mothed2）算法的预测精度分别提升了0.633%、0.582%，并且迭代次数分别减少了6次、4次。因此，通过SPSONN-DNN算法可以提高电量的预测精度，以此来减少发电量，从而减少能源的浪费。

[ 参 考 文 献 ]

[1] GYAMFI S， KRUMDIECK S. Scenario analysis of residential demand response at network peak periods[J]. Electric Power Systems Research， 2012， 93（01）：32-38.

[2] KUN XIE， HONG YI， GANGYI HU， et al. Short-term power load forecasting based on Elman neural network with particle swarm optimization[J]. Neurocomputing， 2019， 416（11）： 136-142.

[3] GUNDU V， SIMON S P. PSO-LSTM for short term forecast of heterogeneous time series electricity price signals[J]. Journal of Ambient Intelligence and Humanized Computing， 2020， 12（02）： 2375-2385.

[4] YIN L， SUN Z， GAO F， et al. Deep forest regression for short-term load forecasting of power systems[J]. IEEE Access， 2020， 8：49 090-49 099.

[5] NIU D， SHI H， LI J， et al. Research on short-term power load time series forecasting model based on BP neural network[C].∥2010 2nd International Conference on Advanced Computer Control， 2010.

[6] 郭海燕， 李英娜， 李川. 基于模拟退火算法优化BP的短期负荷预测控制策略[J]. 陕西理工大学学报， 2021， 37（01）： 36-42.

[7] YLDZ C， AKGZ H， KORKMAZ D. An improved residual-based convolutional neural network for very short-term wind power forecasting[J]. Energy Conversion and Management， 2021， 28（01）： 113731.

[8] 杨毅， 雷霞， 徐贵阳， 等. 采用PSO-BF算法的微电网多目标电能优化调度[J].电力系统保护与控制， 2014， 42（13）： 13-20.

Research on User Electricity Consumption Prediction Method

Based on Improved Deep Neural Network

CAI Xiang¹，ZHU Li²

（1 School of Electrical and Electronic Engineering， Hubei Univ. of Tech.，Wuhan 430068， China；

2 Hubei Provincial Key Laboratory of Solar Energy Efficient

Utilization and Energy Storage Operation Control，

Hubei Univ. of Tech.， Wuhan 430068， China）

Abstract：With the rise of artificial intelligence， researchers have widely used deep neural networks in the field of electric power. However， due to the uncertainty of the parameters of neurons in the hidden layer of deep neural networks， the prediction accuracy of electric power is low， resulting in an imbalance between the supply and demand of electric power and in power redundancy. To this end， we propose the Sin Particle Swarm Optimization Number of Neurons of Deep Neural Networks （SPSONN-DNN） algorithm， which is based on the mutation operation and inertia weight of the particle swarm algorithm improvement， to optimize the parameters of the hidden layer neurons of the deep neural network. The experimental results show that compared with DNN， extreme gradient boosting， linear regression， and the two improved PSONN-DNN algorithms， the prediction accuracy of the SPSONN-DNN algorithm is improved by 1.926%， 2.820%， 1.500%， 0.633%， and 0.582%， respectively; Compared with the two improved PSONN-DNN algorithms， the DNN algorithm reduces the number of iterations by 6 and 4 times， respectively.

Keywords：power prediction; deep neural network; particle swarm optimization; prediction accuracy

[責任编校：张岩芳]