基于变量分组降维的辛烷值损失预测模型

申平 田德生

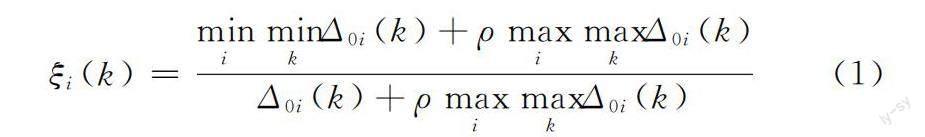
[摘 要]针对精炼汽油辛烷值损失的问题，基于灰色关联度分析方法与最大信息系数方法，给出变量分组降维的特征选择方法，以有效选择出具有独立性代表的特征；与随机森林算法相结合，提出一种辛烷值损失量预测模型。由于操作变量之间具有高度非线性和相互强耦联的关系，采用变量分组降维，即考虑操作变量、性质变量与产品硫含量、辛烷值损失的关系来筛选特征。利用灰色关联度筛选出对辛烷值损失和产品硫含量的关联程度较强的特征，排序后由最大信息系数筛选出28个独立变量。收集研究生数学建模竞赛试题数据，采用随机森林算法进行仿真预测计算。计算结果表明，基于变量分组的特征选择和辛烷值损失预测模型得到的均方误差为0.0086，拟合值R²为92.5%。

[关键词]变量分组; 灰色关联度; 最大信息系数; 随机森林; 辛烷值损失预测

[中图分类号]TE62[文献标识码]A

成品汽油是由原油经过一系列的工艺加工而成，其中催化裂化就是将原油中40%～60%重油轻质化的一个重要工序，经过这一工序得到的催化裂化汽油具有高硫、高烯烃的缺点，为了达到可使用的汽油质量要求，就必须进行脱硫和降烯烃的精制处理。在对催化裂化汽油进行脱硫和降烯烃的精制过程中，往往会导致汽油辛烷值下降。

高品质的汽油具有较高的辛烷值和低的含硫量。影响辛烷值损失的因素包括原料性质、待生吸附剂性质、再生吸附剂性质和产品性质等变量以及300多个操作变量（控制变量）。辛烷值是反映汽油燃烧性能的重要指标，人们把它作为汽油的商品牌号（例如89#、92#、95#），它的高低直接与经济收益相联系。为了经济效益的最大化，在减少环境污染（即控制硫含量）的基础上，进行降低辛烷值损失研究就显得尤为重要，权衡深度脱硫与辛烷值损失之间的關系，也成为人们关注的问题。很多学者在影响汽油辛烷值损失因素、优化降低辛烷值损失的操作变量等方面进行广泛研究。高洁等^[1]为了降低辛烷值损失，制定了优化操作条件的相关措施；齐万松等^[2]采用吸附剂低活性、降低氢油比、提高反应温度等操作条件去降低汽油脱硫的辛烷值损失；黄宏林等^[3]在分析装置辛烷值损失原因后制定了优化调整措施，分阶段进行优化调整装置的参数，优化调整后产品辛烷值损失得以降低；张玉瑞等^[4]经过调和实验，建立了非线型回归模型，调和辛烷值模型的预测模型。

学者大多侧重于化工过程的建模研究，即在化工条件下降低辛烷值损失因素的研究。实际上，由于炼油工艺过程的复杂性以及设备的多样性，操作变量（控制变量）之间具有高度非线性和相互强耦联的关系，若是采用化工过程建模研究，仅仅通过数据关联或机理建模的方法来实现优化控制，往往达不到理想的效果。因此，笔者采用不同的方法建立辛烷值损失预测模型。这个问题涉及变量数量众多，对于有大量变量的工程技术应用问题经常采取先降维后建模的方法。由于不同的变量相互耦联关系强度不同，且它们对辛烷值损失的影响程度不一样，因此本文在进行变量降维之前先对变量进行分组，对不同的组别分别进行降维，确定筛选出主要变量后，再建立辛烷值损失预测模型。

本文研究的是精炼汽油生产过程辛烷值损失量的预测问题，这也是一个涉及变量多的非线性问题，常用的统计方法解决这类问题都不奏效。为了达到良好的预测效果，采取变量分组降维思路结合灰色关联度与最大信息系数方法，处理高维变量降维问题。文本数据集来源于2020年“华为杯”第十七届中国研究生数学建模竞赛B题。数据中有7个原料性质变量、2个待生吸附剂性质变量、2个再生吸附剂性质变量和354个操作变量。先通过过滤型算法方差选择法去掉方差小的变量；再根据对催化裂化汽油精制脱硫装置的工艺操作特点，将变量分为操作变量组和性质变量组。对不同组别分别计算变量与产品汽油的辛烷值和含硫量的灰色关联度，得到一个排序（显示这些变量对辛烷值损失和产品硫含量的关联性程度）；之后运用最大信息系数计算变量之间的信息系数，确定筛选出具有代表性和独立性的变量；最后采用随机森林算法进行辛烷值损失量的预测。

1 主要原理和核心算法

针对变量数量多且不同的变量相互耦联关系强度不同的情况，本文采取分组降维，采取的方法是灰色关联度法和最大信息系数法。灰色关联度法对于变量间相互耦联关系强度不同的排序问题具有优势，最大信息系数方法更适合筛选出独立特征（变量）。最大信息系数能够将最大的特征去除，得到相对独立的特征去除相关性较大的特征，在保证特征关联度的同时也考虑特征之间的独立性，使选择的特征尽可能具有独立性和代表性。

在建立预测辛烷值损失模型时，本文选择随机森林预测算法。这种算法在很多数据集上建立随机的树，树与树之间（即特征子集之间）具有相互独立的特点，因此以部分的特征数据进行预测，仍可以维持结果准确度。

1.1 灰色关联度分析

灰色关联度（GRA）^[5]可以通过对比参考数据列与比较数据列的相似程度去衡量两者的关系是否具有关联性。关联系数

其中：Δ_0i（k）表示第k点X₀与X_i的绝对差；ρ为分辨系数，其作用是减少因Δmax数值失真而导致的误差，ρ一般取0.5。

1.2 最大信息系数

最大信息系数（MIC）^[7]主要用于衡量两个变量X和Y之间的线性或非线性耦合关联强度。

设X，Y是取值于数据集D中的两个随机变量，两个随机变量（X，Y）联合概率密度函数为p（x，y），边缘概率密度函数为p（x）和p（y），定义两个随机变量取值x和y之间的互信息为

将数据集D 中两个随机变量的不同取值用网格分布的方式划分，即将随机变量X和Y的取值分别划分为a个网格和b个网格，形成a×b个网格划分。由于随机变量X和Y取值的随机性，它们在不同的网格划分方法中的分布也不同，将不同网格划分方法中的互信息MI（x；y）的最大值作为最大互信息值。经过归一化处理可得最大信息系数MIC的表达式^[8]为

其中，B（n）=n^0.6。最大信息系数的取值在[0，1]之间，取值越接近1，代表随机变量X、Y之间的依赖关系越强；取值越接近0，代表随机变量X、Y之间的依赖关系越弱。

1.3 随机森林预测算法

随机森林算法（RF）是一种有监督学习算法，在处理分类和回归问题方面具有优越的性能。它通过构建多棵相互独立的决策树组成的森林来完成决策、分类和回归的任务^[9]。经过训练后，算法中设立森林的每一棵决策树会分别对新输入的样本进行预测，由多颗树预测值的均值决定最终预测结果。

构造随机森林算法的步骤为3步^[15]：1）确定用于构造的树的个数；2）对数据进行自助采样；3）基于新数据集构造决策树。

2 结果

2.1 数据的收集

本文数据集来源于2020年“华为杯”第十七届中国研究生数学建模竞赛B题（https： //cpipc.chinadegrees.cn//cw/4924b7f01749981b29502e9）。该数据集是某石化企业的催化裂化汽油精制脱硫装置积累的大量历史数据，包括从催化裂化汽油精制装置采集的325个数据样本，每个数据样本中有7个原料性质变量、2个待生吸附剂性质变量、2个再生吸附剂性质变量（以上被称为性质变量）和354个操作变量。这些数据采自于中石化高桥石化实时数据库（霍尼韦尔PHD）及LIMS实验数据库。其中操作变量数据来自于实时数据库。

2.2 计算结果及分析

2.2.1 数据预处理

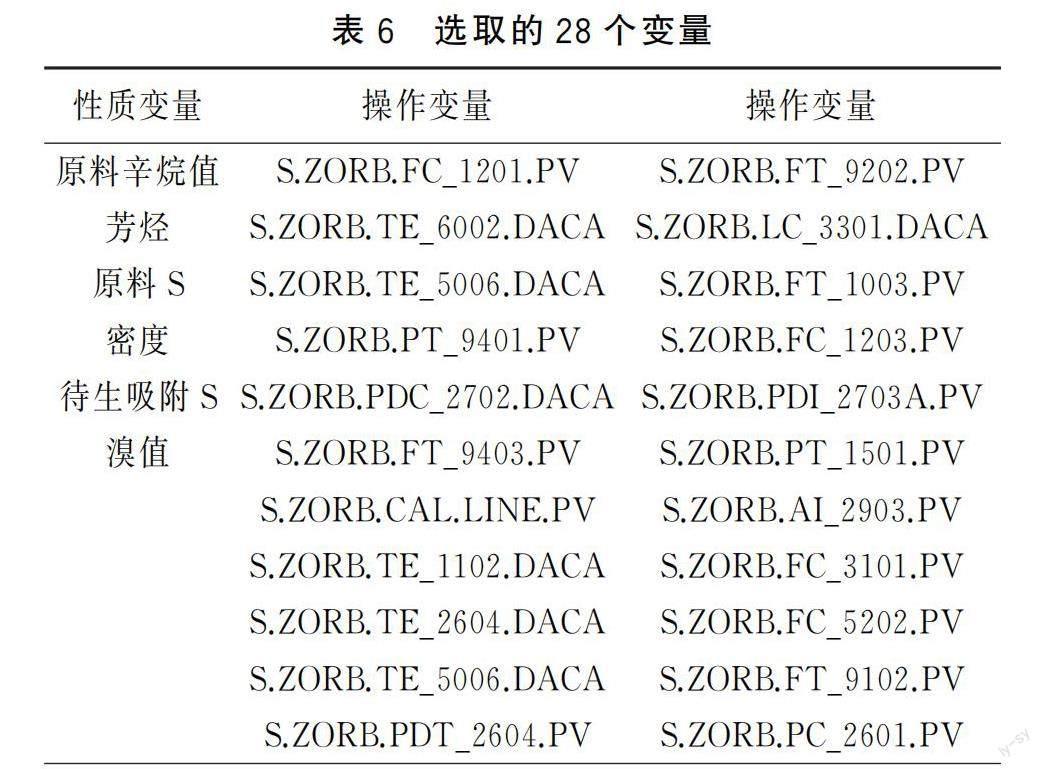
1）去除异常值 去除异常值的根据是3σ原则处理，并采用3σ边缘数值进行替换。对于超过操作变量取值范围的变量，删除异常比例为较高的操作变量，即删除7个变量，它们是S.ZORB.TE_2005.PV，S.ZORB.PT_9403.PV，S.ZORB.LC_1201.PV，S.ZORB.FT_1004.TOTAL，S.ZORB.FT_9101.TOTAL，S.ZORB.TE_5007.DACA，S.ZORB.PT_2106.DACA.PV。处理后的数据包含11个性质变量和347个操作变量。

2）线性过滤法预处理 线性过滤法预处理就是对数据进行相关性和共线性的度量处理，删除数据中的方差较小变量。这一过程中，对于347个操作变量，去除强共线性>0.9的138个操作变量，剩下209个操作变量。10个性质变量保持不变。

2.2.2 特征的选取

1）变量分组降维 考虑到数据性质变量和操作变量与对辛烷值损失的不同影响程度，故将变量分为性质变量组和操作变量组。通过Python语言计算灰色关联度选出变量，将因变量辛烷值损失和产品硫含量分别作为参考序列，分组后的变量作为自变量序列，分开分析筛选变量。将变量进行归一化处理（区间化），采用式（1）计算出关联系数，计算出10个性质变量与209个操作变量分别对产品硫含量和辛烷值损失的灰色关联度，计算结果如表1和表2。

根据表1和表2结果，将得到的灰色关联度进行排序。为保证选取的变量在30个以内，在选取与产品硫含量较大关联度的变量时，可选取GRA1>0.5644的前6个性质变量、GRA2>0.8244的前20个操作变量，共26个变量；在选取与辛烷值损失较大关联度的变量时，可选取GRA2>0.6990的前6个性质变量、GRA4>0.7602的前24个操作变量。表3和表4分别表示选出的变量对于产品硫含量和辛烷值损失的灰色关联度排序。

对表3和表4筛选出的变量进行汇总，去掉重复和关联度相对较低的变量，最终选出8个性质变量和39个操作变量，共计47个变量（表5）。

2）独立性的判别 为了去除表5中具有较为复杂耦合关系的变量（独立性较差），采用最大信息系数方法进行筛选。运用R软件对式（2）计算出的47个变量之间的互信息进行编程，将其代入式（3），得到特征之间的最大信息系數。最大信息系数的图像如图1a所示。

在图1中，横纵坐标表示不同的变量，中间的圆形色点色度代表两个变量之间最大信息系数的强弱，偏向红褐色表明两个变量之间的相关性强度较强。色度变化范围为0～1，其值越接近1，颜色越接近红褐色。

为选出独立性强的变量，首先剔除最大信息系数大于0.5的变量。通过对辛烷值的模拟计算和结果对比，选取28个变量，其中性质变量6个，操作变量22个（表6）。

对选择出28个变量（特征），计算28个重要特征的最大信息系数，如图1b所示。图1b中色点颜色值均在0.5以下，这表明变量之间耦合关系不强，即所选变量具有较好的独立性。

2.2.3 辛烷值损失预测结果与分析 对辛烷值损失预测计算，拟建立随机森林算法^[10]模型。Scikit-learn工具包是一个开源的基于Python编程语言的机器学习工具库。

1）确定森林中树的数目，即决策数树数目^[11]。在Scikit-learn工具包中RandomForestRegressor函数，决策数树目以参数n_estimators表示。理论上讲n_estimators越大越好，但由于计算机资源的占用会导致训练和预测时间的增加^[12]。在Scikit-learn中n_estimators默认为10，本文通过设定为20，50，80测试，最终设定为50。

2）对数据进行自助采样。从样本集中有放回地重复随机抽取一个样本，共抽取n_sample次，组成新的数据集。新数据集的样本容量与原数据集的相等，本文数据集的样本容量为325。

3）基于新数据集来构造决策树。在每个结点处选取特征的一个子集，选取的特征子集中特征的个数通过max_features参数来控制，一般max_features参数的设置不宜过小。在Scikit-learn中，max_features有以下几种设置：auto，sqrt，log₂，None^[12]。这里设置为None。

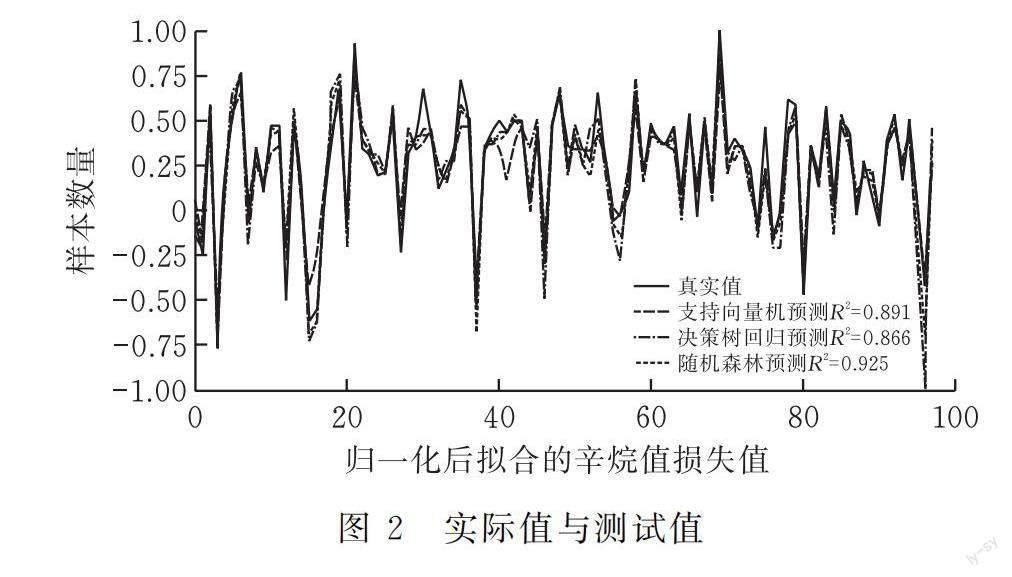
在计算中，产品辛烷值作为被解释变量，变量数据进行归一化处理后，将随机选取的228个样本数据作为训练集数据，选取97个样本数据作为测试集数据，利用测试集数据对拟合好的模型进行辛烷值损失的预测。计算结果见图2。

图2中：红色的曲线为真实值的波动情况；绿色为随机森林模型^[13]预测曲线，拟合值R²为92.5%；蓝色的曲线为支持向量机回归模型^[14]预测曲线，拟合值R²为89.1%；浅绿色为决策数回归模型^[15]预测曲线，拟合值R²为86.6%。从图2可知，基于随机森林算法的预测值曲线与真实值曲线的重叠程度最高，说明所建立的预测模型预测效果较好。

比较不同的算法预测模型的预测性能。表7为预测性能评价指标MSE值、MAE值、R²的值。

从表7结果可知，本文使用的随机森林算法的均方误差（MSE）为0.0086，平方绝对误差（MAE）为0.0653，MSE和MAE值均比支持向量机回归和决策树回归的小，这进一步说明随机森林算法的预测精度优于支持向量机回归和决策树回归，而且基于变量分组降维的随机森林算法的可决系数达到92%以上。在模型能力的解释方面，该方法能解释样本数据中92%以上的信息，体现其具有合理性。

3 结束语

针对选取具有独立性和代表性的重要特征，以及建立预测辛烷值损失预测模型的问题，提出了基于变量分组的特征选择和辛烷值损失预测模型。通过变量分组，将性质变量和操作变量分别处理，分析其与产品硫含量、辛烷值损失的关系；通过灰色关联度方法得到关联度强的特征，排序进行筛选；再利用最大信息系数筛选出独立性特征，最终得到28个特征。在预测模型方面，采用随机森林构建辛烷值损失预测模型，与支持向量机回归和决策树回归算法比较，构建的随机森林辛烷值损失预测模型得到的均方误差为0.0086，R²为92.5%。通过将变量分组并采取融合灰色关联度分析方法和最大信息系数方法，在选择具有代表性特征的同时，更保证操作变量之间的独立性。

[ 参 考 文 献 ]

[1] 高洁，王莉娟，孙丽琳. 优化操作条件降低汽油辛烷值损失[J]. 石油化工应用，2011， 11（11）：97-101.

[2] 齐万松，姬晓军，侯玉宝，等. SZorb装置降低汽油辛烷值损失的探索与实践[J].炼油技术与工程， 2014，44（11）：5-10.

[3] 黄宏林，李烨，谷晓琳. 优化操作条件降低汽油加氢装置辛烷值损失[J]. 石油化工应用， 2015， 34（12）： 116-118.

[4] 张玉瑞，陈微微，周晓龙，等. 一种改进的调合辛烷值模型预测汽油研究法辛烷值[J]. 石油炼制与化工， 2011，1（03）：14-28.

[5] 江世艳，王燕青，徐越峰，等. 基于灰色关联分析的电网安全事故关键致因分析[J].中国电力，2020（10）：56-59.

[6] 张晓娜. 我国服务业与城镇化的灰色关联度实证考察[J]. 统计与决策，2020（09）：97-100.

[7] RESHEF D N， RESHEF Y A， FINUCANE H K， et al. Detecting Novel Associations in Large Data Sets[J].Science， 2011，334（6062）： 1518-1524.

[8] 张莹，杜井涛，吴怀岗. 基于最大信息系数的主成分分析贝叶斯分类算法[J]. 信息与电脑， 2020，32（11），63-66.

[9] TIN K H. The random subspace method for constructing decision forests[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1998， 8（10）： 832-844.

[10]YU F B， WEI C H， DENG P. Deep exploration of random forest model boosts the interpretability of machine learning studies of complicated immune responses and lung burden of nanoparticles[J]. Science Advances， 2021， 5（26）： 7-22.

[11]盧维学，吴和成，万里洋. 基于融合随机森林算法的PLS对降水量的预测[J]. 统计与决策.2020，8（18）：27-31.

[12]暮雪成冰，随机森林n_estimators参数max_features参数[EB/OL].[2019-06-19]https：//blog.csdn.net/u012768474/article/details/92829985.

[13]BREIMAN L. Random forests[J]. Mach Learn，2001， （45）： 5-32.

[14]周洲，焦文玲，任乐梅，田兴浩. 蚁群算法分配权重的燃气日负荷组合预测模型[J].哈尔滨工业大学学报，2021（06）：177-183.

[15]王马强. 数据挖掘方法在信用卡违约预测中的应用[D]. 武汉：华中师范大学.2020.

Feature Selection and Octane Number Loss Prediction

Model Based on Variable Grouping

SHEN Ping， TIAN Desheng

（School of Science， Hubei Univ. of Tech.， Wuhan 430068，China）

Abstract：This paper studies the octane number loss of refined gasoline. In order to effectively select the features with independent representation， based on the grey relational analysis method and the maximum information coefficient method， the feature selection method of variable grouping dimension reduction is given. Combined with stochastic forest algorithm， a prediction model of octane number loss is proposed. In view of the highly nonlinear and strongly coupled relationship among operational variables， variable grouping is adopted to reduce dimension， that is， the relationship between operational variables and property variables and sulfur content and octane number loss of products is considered to screen features. The features with strong correlation between octane number loss and sulfur content of products were screened by grey correlation degree， and 28 independent variables were screened by maximum information coefficient after sorting. The data of postgraduate mathematical modeling contest are collected， and the random forest algorithm is used for simulation and prediction calculation. The calculation results show that the mean square error of feature selection and octane number loss prediction model based on variable grouping is 0.0086， and the fitting value R²is 92.5%.

Keywords：variable grouping; grey correlation degree; maximum information coefficient; random forest; octane number loss predict

[責任编校：张 众]