基于Gabor小波和SSA优化的SVM人脸表情识别研究

张 辉,王 杨,,王子凡,朱强军,张广海

(1.安徽师范大学皖江学院 电子工程系,安徽 芜湖 241003;2.安徽师范大学 计算机与信息学院,安徽 芜湖 241000)

0 引言

自20世纪60年代出现人脸识别技术以来,至今已有大半个世纪的发展史。人脸识别技术也在人们的生活之中得到了广泛的应用。随着人工智能技术的发展,用智能技术去识别生物特征已成为目前最受欢迎的技术之一。人脸表情蕴含着大量的信息,从表情中可以提取出非常丰富的信息,在商业方面,可以根据顾客的喜好进行商品的推荐;在教育方面,表情识别可以监控学生在课堂上的状态,从而达到更好的教育水平,在交通安全方面,可以监控驾驶员的是否疲劳,减少交通事故的发生。基于人工智能的方法去识别人脸表情已成为目前的研究热点。

人脸表情识别一般包括4步[1]。第1步,进行图像采集,既包括静态的采集,也包括动态的采集;第2步,进行图像中人脸的检测和定位,目的是定位人脸在图像中的位置坐标;第3步,图像的预处理,因为在采集图像的过程中不可避免地会有一些噪声的干扰;第4步,特征提取和通过分类器进行分类。人脸表情识别技术的关键在于特征的提取,特征提取的好坏可以直接影响到算法的识别结果。人脸表情识别最早是基于几何结构的算法、基于隐马尔克夫法等。目前的主流特征提取有基于局部二值特征模式(local binary patterns,LBP)[2]、基于局部方向的模式(local directional pattern,LDP)[3]、Gabor小波+主成分分析法[4]。随着深度学习的发展,新的方法不断出现,如基于卷积神经网络(convolutional neural networks, CNN)[5-6]、基于生成式对抗网络(wasserstein generative adversarial net,WGAN)[7]等。

本文提出了一种基于Gabor小波和麻雀搜索算法(sparrow search algorithm,SSA)优化支持向量机(SVM)的人脸表情识别方法。实验在JAFFE数据集和CK+数据集进行训练和测试,使用Gabor小波先对图像进行特征提取,将提取之后的特征输入到主成分分析法(principal component analysis,PCA)进行降维,把降维之后的特征用麻雀优化算法优化之后在SVM之中进行表情分类。麻雀优化算法的优点是快速而且准确地搜索到SVM的核函数参数c和惩罚参数g,从而达到快速训练的目的。通过实验和分析得出,本文所提算法在正确率上达到比较高的程度,在寻优速度方面领先于传统的网格搜索法。

1 Gabor小波纹理特征提取

目前,对数字图像的处理主要可以分为两个方面,分别为空域和频域。空域也就是空间域,是指对图像进行像素级的处理;频域是通过将数字图像从像素级别转换成频率级别进行分析。频域分析法在目前的图像处理技术中有着广泛的应用,例如,在可以利用频率成分和图像外表之间的关系,将一些空域上很难表述的任务变得简单,滤波在频率域更加直观,它可以解释空间域滤波的某些性质。从空域分析变换成频域分析就要用到傅里叶变换。傅里叶变换将空域变换成频域,为图像的处理提供了一个新的方法。但是傅里叶变换有很大的局限性,因为,在对数字图像进行变换时是对整个时域图像进行积分变换,很难关注到一些局部的变化,导致傅里叶变换很难提取到图像的边缘特征,不利于纹理特征的提取。

为了解决傅里叶变换的缺点,D·Gabor在1946年提出了Gabor小波变换[8],在变换之中引入了时间局部变化的窗函数,使图像的边缘特征明显,更加能够关注到图像的局部空间变化,Gabor小波对图像的边缘敏感,能够提供良好的方向选择和尺度选择。设f为具体的函数,且f∈L2(R),则Gabor变换的定义式为

(1)

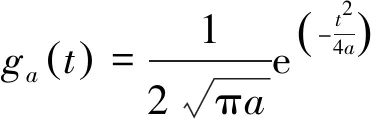
(2)

信号重构的表达式为

(3)

Gabor小波是由Gabor变换推导而来,其中二维的Gabor小波的表达式为

(4)

式中:γ表示Gabor滤波器的方向;δ表示滤波器的频率;z表示图中像素的坐标;σ表示滤波器的方向;i是算子,为复数。

2 麻雀优化算法优化的SVM

2.1 SSA优化算法原理

麻雀搜索算法是2020年XUE et al[9]提出的一种智能优化算法。算法主要模拟麻雀的觅食行为和反捕食行为。算法比较新颖,具有寻优能力强,收敛速度快等特点。主要的规则如下:

该算法将麻雀的种群按个体在种群中的分工分为发现者和跟随者。

1)发现者通常在种群中储存较高的能量,负责在整个种群中寻找食物丰富的区域,并为所有参与者提供觅食的区域和方向。在建立模型时,能量储备的高低取决于个体麻雀的适应度值。

2)当麻雀发现捕食者时,个体麻雀会发出警报信号。如果报警值高于安全值,发现者会将跟随者带到另一个安全的地方进行觅食。

3)发现者和追随者的身份是动态不固定的。只要能找到更好的食物来源,每只麻雀个体都可以成为发现者,但发现者和追随者在整个种群中的比例保持不变。换句话说,当一只麻雀个体成为发现者时,另一只麻雀个体成为追随者。

2.1.1发现者位置更新

(5)

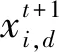
2.1.2更新跟随者位置

(6)

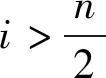
2.1.3侦查预警行为

(7)

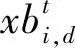
麻雀优化算法主要是不断的迭代更新发现者和跟随者的位置,最终找到全局的最优值,本算法的主体流程如图1所示。

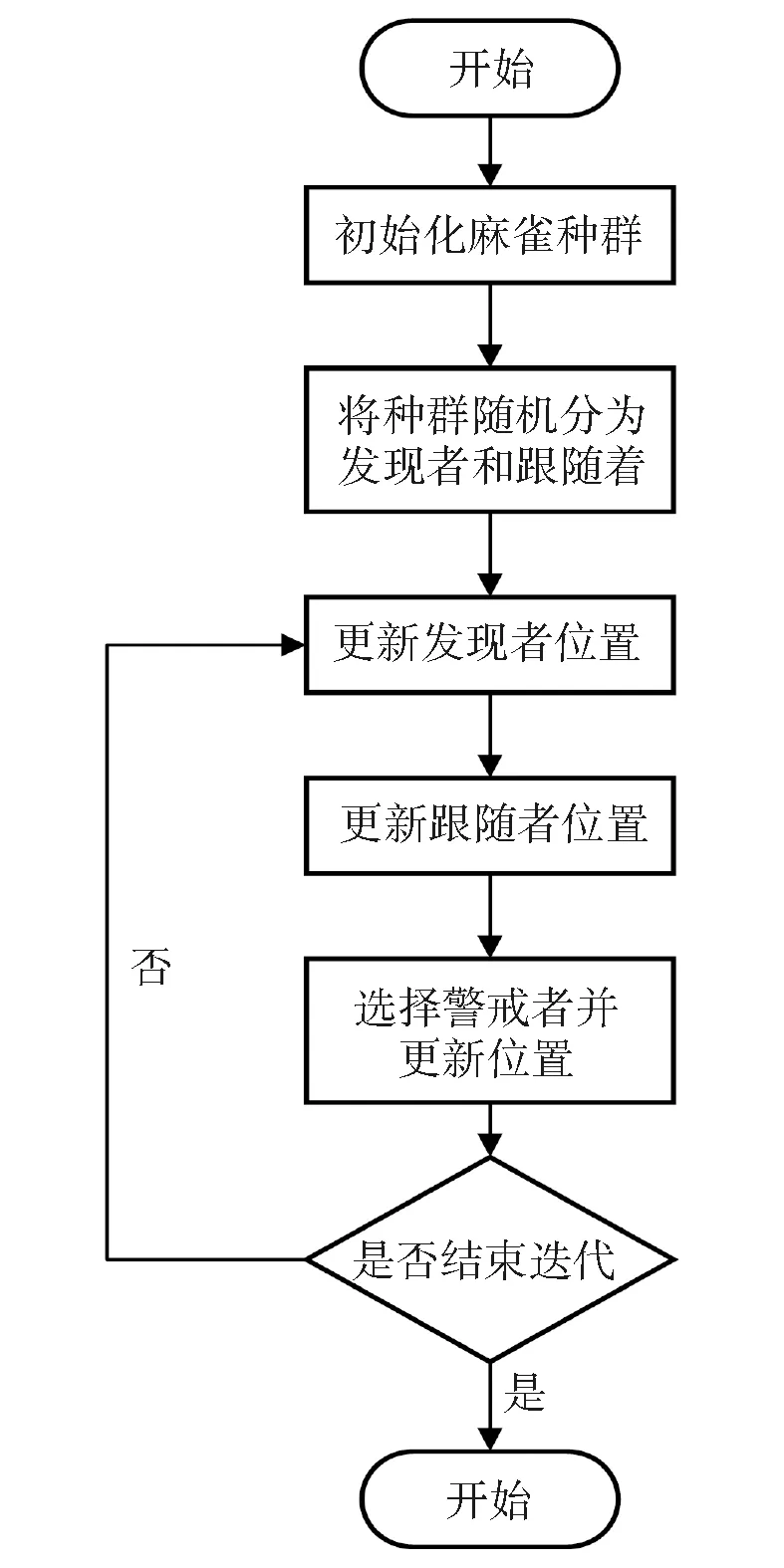
图1 麻雀搜索算法优化流程

2.2 主成分分析法(PCA)

主成分分析法(PCA)是一种对多维特征进行降维的算法。在用SVM分类器对数据进行分类之前,如果输入的特征维度较高,就要对特征的维度进行降维。PCA就是目前应用最为广泛的数据降维算法。

PCA算法的主要思想是将在特征中关系可能比较紧密的变量,通过计算将其变成尽可能少的变量,这些新的变量能够最大程度地保留原来的特征,去除原来的冗余特征,使维度变低,减少样本的存储空间,能够加速计算速度,减少训练模型出现过拟合的情况。

2.3 支持向量机算法(SVM)

支持向量机(SVM)是一种有监督方式的机器学习算法。机器学习算法是能够按照监督的方式很好地完成二分类的广义线性分类器。SVM是在特征空间中最大化间隔的线性分类器。将SVM进行推广即可以完成数据线性不可分的问题。首先,SVM通过选择一个核函数K,将低维的非线性数据映射到高维的空间中。在高维空间中完成线性分割,构造出最优分类超平面。

核函数是计算两个向量在隐式空间映射后空间中的内积函数。核函数的定义为

φ(x)X→H

(8)

式中:X为输入特征;H为映射之后的希尔伯特空间特征。使所有的x,y∈X函数K(x,y)=φ(x)φ(z),则K(x,y) 为核函数;φ(x) 为映射函数;φ(x),φ(y)为x,y映射到特征空间的内积。

目前主要的核函数有:

线性核函数,主要用来解决线性可分的数据,直接在原始空间进行分类,对于线性可分数据,其表现良好;多项式核函数,可以将低维的输入特征空间映射到高维的输入特征空间,比较适用于正交归一化的数据;高斯核函数,是一个局部性很强的核函数,目前应用非常广泛。

本实验采用高斯核函数。

高斯核函数也称径向基函数,其定义式为

(9)

式中:x′ 为核函数中心;x-x′2为x和x′ 的欧式距离,值随两个向量之间的距离增加而增加;σ2控制着核函数的作用范围。核函数无论是在大样本还是小样本数据中都有着很广泛的应用。

2.4 使用SSA优化SVM

SVM中的核函数参数c与惩罚参数g会直接影响SVM分类器的分类性能。核函数参数c过大,会造成模型结构复杂,容易出现过拟合;核函数参数过小,会造成模型结构过于简单,对样本的拟合能力就会下降。而惩罚参数g过大或过小,都会在测试时导致泛化能力下降。因此选择一对合适的核函数参数c与惩罚参数g是SVM分类器分类性能高低的关键。使用SSA优化SVM就是对SVM的核函数参数c与惩罚参数g进行寻优。算法主要步骤如下:

1)初始化麻雀种群规模的总数,确定最大迭代次数,分配发现者和跟随者的比例,并确定需要优化参数的个数及每个参数的上限1、上限2,下限1、下限2。

2)计算种群之中每个麻雀的适应度,并为其分配种类。

3)根据公式(5)-公式(7),对麻雀种群进行位置更新,并重新计算每个麻雀的适应度,重新分配麻雀种类。

4)是否达到最大迭代次数,若未达到继续执行步骤3,若达到则结束迭代。

5)计算种群中最优位置的适应度,所对应的位置就为最优的核函数参数c与惩罚参数g。

3 实验设计及分析

3.1 数据集和实验设备描述

本文采用的数据集为JAFFE和CK+人脸表情数据库。

JAFFE数据集一共有213张图片,分别来自10名日本女学生。每人做出7种表情,分别为愤怒、厌恶、恐惧、高兴、悲伤、惊讶、中性。每种表情的数量分布如表1所示。

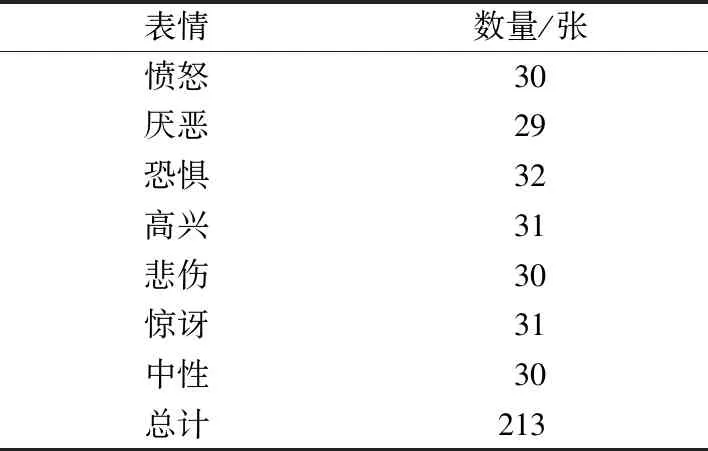
表1 JAFFE每种表情的数量分布

CK+数据集[10]由123名年龄从18岁到30岁的参与者组成,共593张图片序列。7种表情分别为愤怒、厌恶、恐惧、高兴、悲伤、惊讶、蔑视。本实验从每次序列中提取最后3个帧,共981张图片。每种表情的数量分布如表2所示。

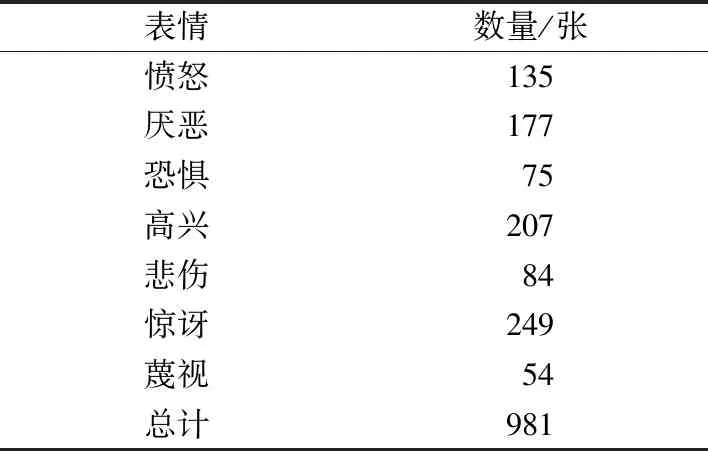
表2 CK+每种表情的数量分布

采用MATLAB R2021a进行实验,在Intel(R) Core(TM) i5-7300HQ 2.50 GHz,8 GB内存,win10的设备上进行。

3.2 实验过程设计

本文结合Gabor小波、麻雀搜索算法、快速主成分分析法、支持向量机技术,完成对7种人脸表情的分类。通过Gabor小波技术先进行图片纹理特征提取,之后,通过快速主成分分析法进行降维,将降维之后的数据输入SVM分类器。将人脸分类器分为两组,一组用于训练,剩下的用于测试。算法的主要步骤如下:

1)完成人脸表情数据库的训练集和测试集的分类,将训练集输入Gabor小波进行纹理提取,每个Gabor小波提取的特征有1 440维。

2)由于Gabor小波提取出的特征过高,不能直接输入SVM分类器进行分类。将提取出的特征输入主成分分析法进行降维。

3)将降维之后的特征输入经过麻雀搜索算法优化后的SVM分类器进行分类。

重复1) 和2) 两个步骤,调整测试集和训练集的比例和主成分分析法的维度。

实验总体流程如图2所示。

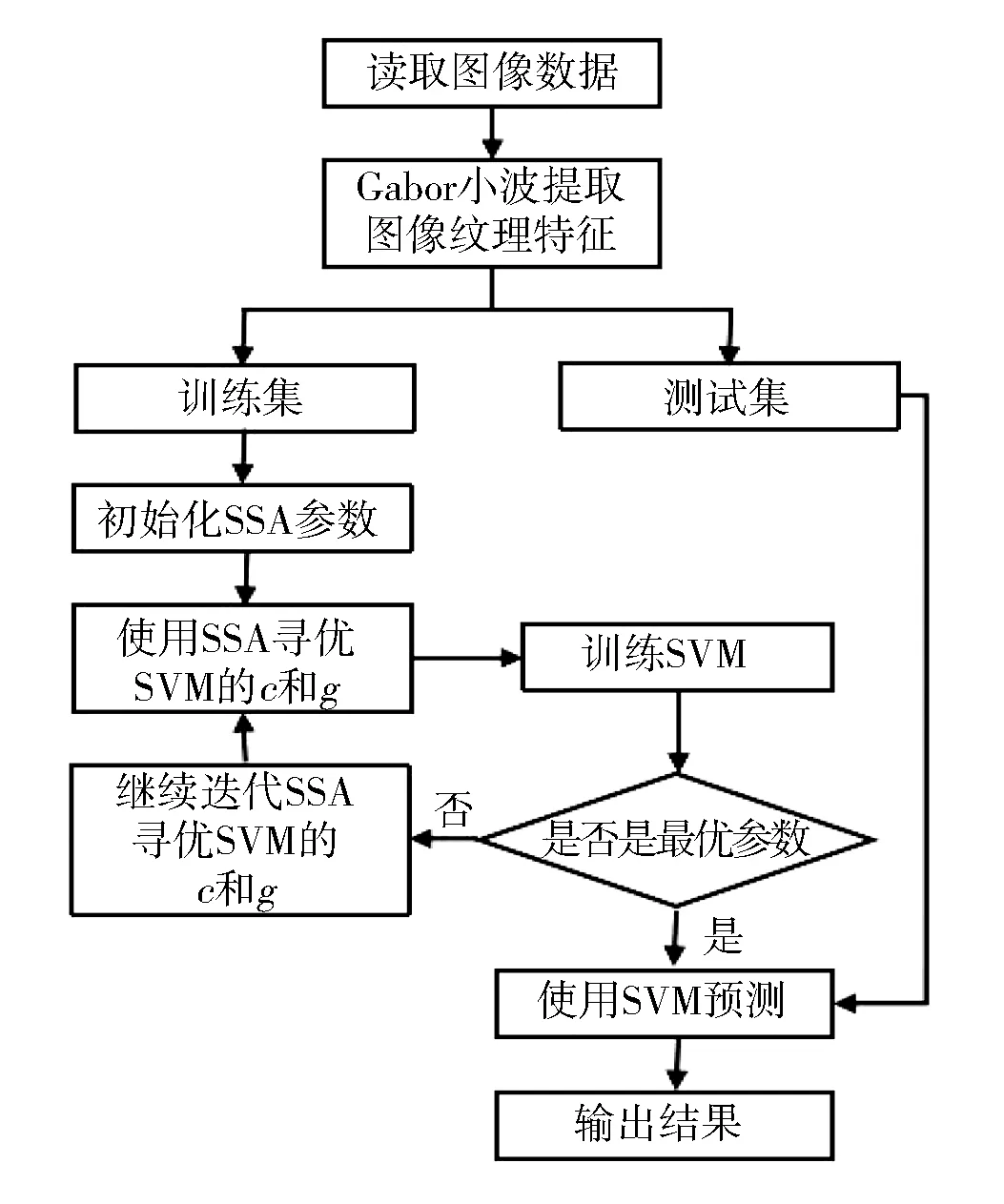
图2 实验总体流程图

3.3 实验结果及分析

JAFFE数据集中划分的数量比例为7∶3或8∶2,每张图片的维度从5维开始。测试的结果如表3所示。

表3 JAFFE数据集测试结果

由表3数据可知,当JAFFE数据集的训练集和测试集的比例达到8∶2且维度达到30维时可以到达最佳的识别率90%,当维度达到30时,正确率不再上升。达到最高识别率时测试集的识别情况如图3所示。

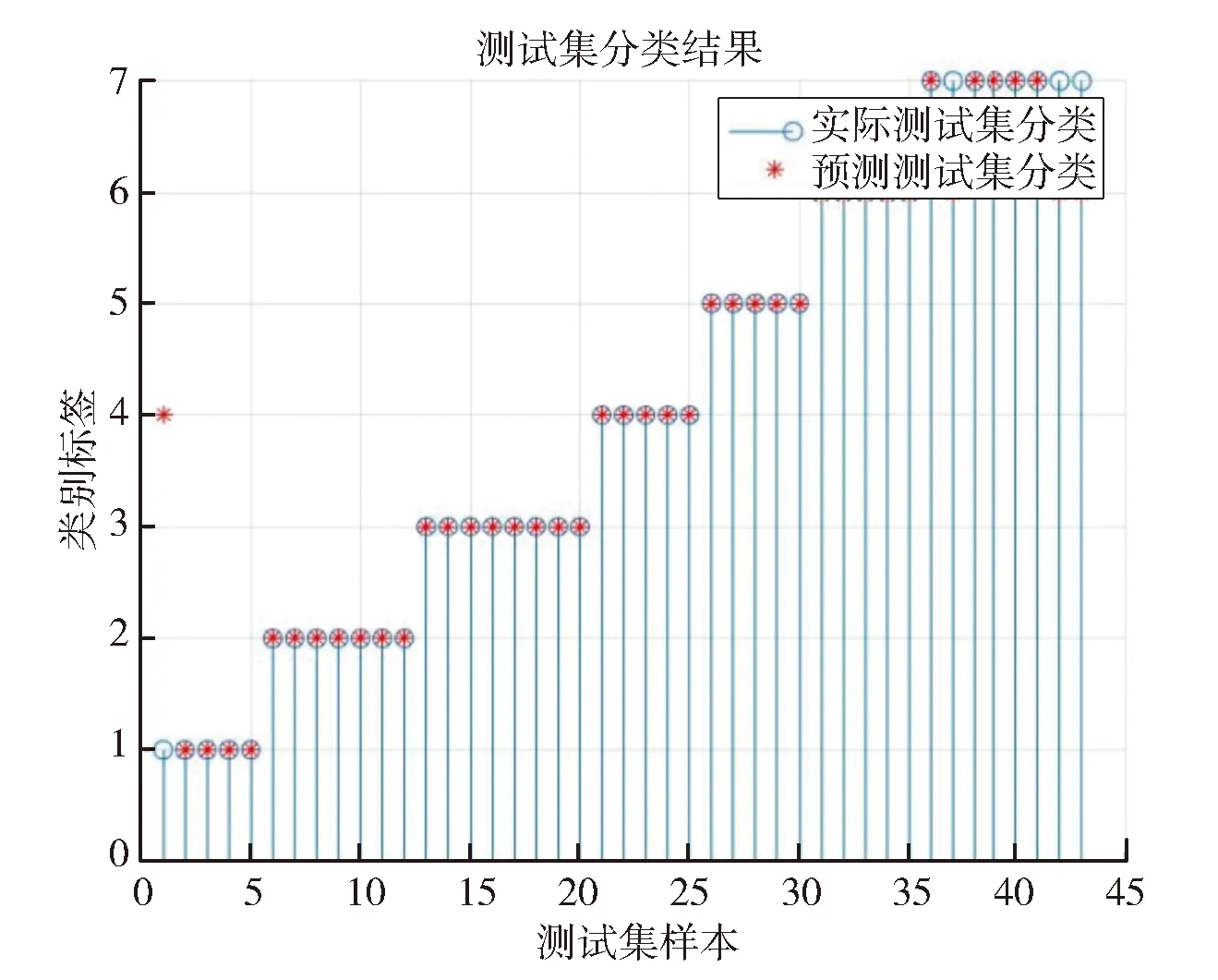
图3 JAFFE数据集的最高识别率图

CK+数据集中训练集和测试集划分的数量比例为7∶3或8∶2,每张图片的维度降到5维开始。每次测试的平均正确率如表4所示。

表4 CK+数据集测试结果

由表4可知,训练集和测试集比例为7∶3或8∶2时都有较高的识别率,当比例为7∶3、维度为15维时,最高识别率可达97%。当训练集和测试集的比例达到8∶2时,在25维就可以达到平均99%的准确率。在CK+数据集上的表现较为优越。当CK+数据集达到最高识别率时,测试集的识别情况如图4所示。

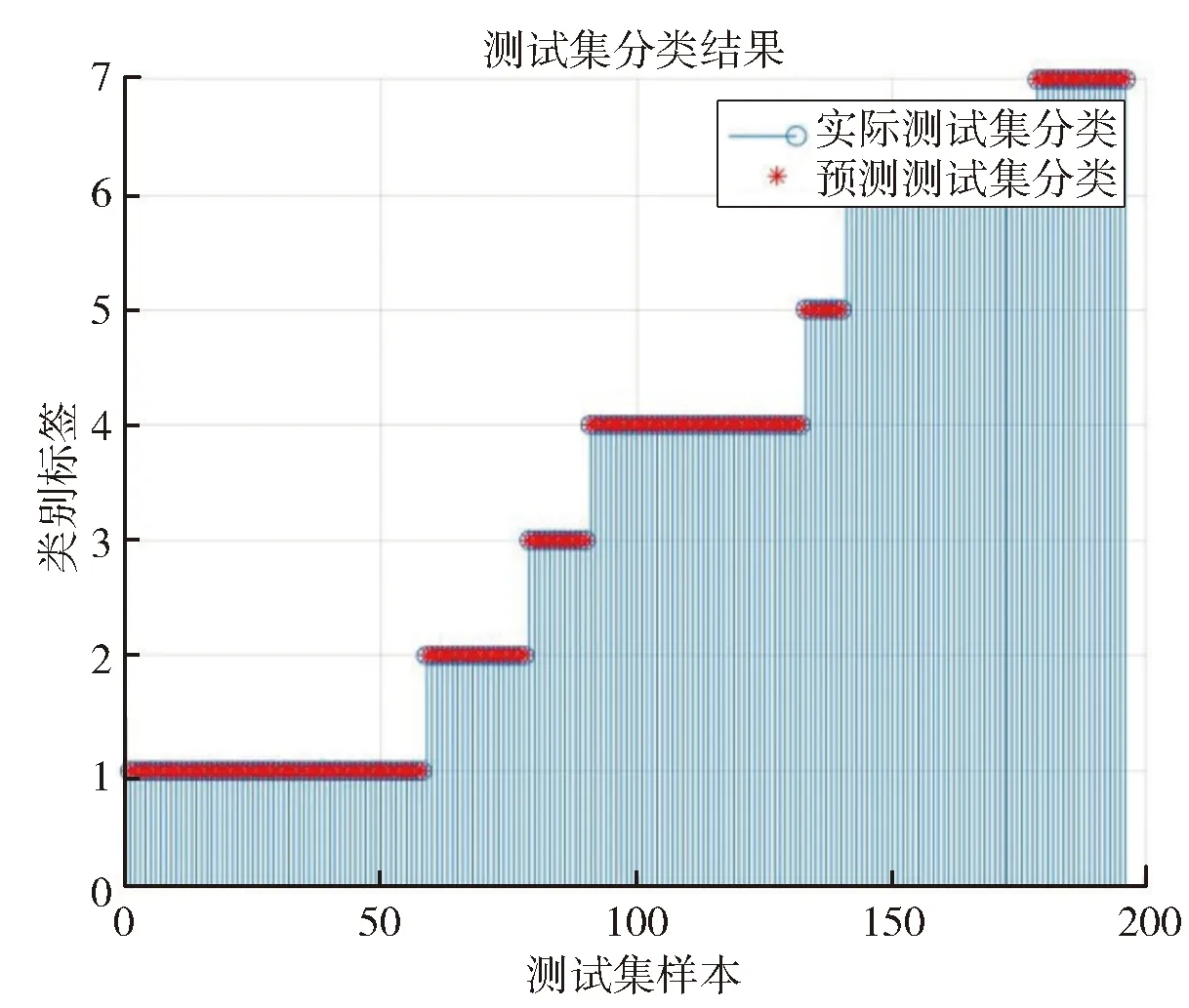
图4 CK+数据集的最高识别率图

由表3和表4可知,本文算法在JAFFE数据集上的识别率最高可以达到90.69%,在CK+数据集上的识别率最高可达99%。

3.4 实验结果对比

3.4.1算法寻优时间对比

在JAFFE数据集上选取训练集和数据集之比为8∶2、主成分分析法降维到35维时,将本文所提麻雀搜索算法(SSA)和传统网格搜索算法优化的SVM进行比较。设置传统网格搜索算法的搜索步长为0.2,将麻雀搜索算法和传统网格搜索算法的时间进行比较,两个算法的平均寻优时间如表5所示。

表5 算法寻优时间的对比

从表5可以看出,本文所采用的麻雀搜索优化算法与传统的网格小步长搜索算法相比,在寻优间上大幅度领先。

3.4.2算法识别率对比

将本文算法与已有的机器学习算法进行对比,在JAFFE数据集上进行实验,训练集与测试集的划分为8∶2,PCA将Gabor小波提取的特征降维到30维,如表6所示,可以看出本文所提算法在正确率上较为有优势。

表6 算法识别率对比

4 结语

针对传统支持向量机的网格搜索算法寻优速度慢,提出了一种采用SSA优化SVM的策略。先对数据集采用Gabor小波提取特征,将提取的特征经PCA降维之后,输入到经SSA优化后得到核函数参数c与惩罚参数g的SVM中进行分类。实验结果表明,本文算法在JAFFE数据集上平均可以达到90% 左右的识别率;在 CK+ 图片序列数据集上最高可达100% 的正确率。将本文所提算法在JAFFE数据集上与传统网格搜索算法对比,其在寻优时间上优势明显。在今后的研究中,还可以针对麻雀搜索算法进行优化改进,根据其在寻优过程中种群数量减少等问题,增加其寻优能力,或者使用特征融合策略进一步提高正确率。