曲率半径和桥面不平度对大跨弯连续刚构桥冲击系数的影响

王俊霞,申 林,郭大虎,卓亚娟,韩智强

(1.山西工程职业学院 交通工程系,山西 太原 030009;2.中路高科交通检测检验认证有限公司, 北京 100088;3.山西裕欣凯工程检测有限公司,山西 太原 030000;4.太原科技大学 车辆与交通工程学院,山西 太原 030024)

0 引言

大跨弯连续刚构桥是采用墩、梁、基础三者固结联成整体、共同参与受力的结构,具有较大的抗弯和抗扭性能,在国内公路建设中应用广泛,如广东洛溪大桥、湖北黄石长江大桥、虎门大桥辅航道桥等均采用此类结构[1]。但随着跨越能力的提高,受多种因素共同影响,尤其是移动荷载作用下,桥梁振动问题较为显著,进而影响车辆的正常行驶。这种车辆与桥梁之间的相互作用问题称为车桥耦合振动。随着科学技术进步和计算机水平的提高,车辆与桥梁间的动力响应引起了相关学者的广泛关注。1844年,英法工程师对Britannia桥进行模型试验,为现阶段可追溯到较早开展车桥振动分析的研究成果[2]。1847年,WILLS推导了忽略桥梁质量的简支梁在移动荷载作用下振动微分方程。1956-1959年,BIGGS等采用数值积分法求解车桥耦合振动问题[3-4]。易晋生等[5]采用达朗贝尔原理,分别组建车辆和桥梁的动力学方程,分析了桥面不平度对简支梁桥动力响应的影响。罗浩[6]采用三轴整车模型,分析了不同曲率半径和桥面不平度对连续梁桥冲击系数的影响,结果表明:曲率半径和桥面不平度均对桥梁的冲击系数有较大影响。综上可知:车桥耦合振动问题在常规桥梁中较为成熟,但大跨弯连续刚构桥由于墩梁固结的受力特点,有关此类桥梁冲击系数的相关研究则相对较少。因此,针对此类桥梁动力响应显著,而计算方法不够健全完善的现状,开展不同曲率半径和桥面不平度对桥梁冲击系数影响的研究具有重要意义,相关成果可为此类桥梁的动力安全评估提供技术支持。

1 车桥耦合基本理论

1.1 基本假定

1)桥梁刚度和阻尼特性均匀分布,横隔板就近布置在相应节点处;2)忽略桥梁横截面翘曲变形的影响;3)忽略桩土效应的影响。

1.2 三轴平面车辆动力学模型

目前,有关车辆动力学模型相对较多[7],包括两轴平面和空间车型、三轴平面和空间车型等,本研究选取了1/2三轴平面五自由度车辆模型进行分析,其中包含车体竖向位移自由度、车体点头自由度、车轮与悬架支撑系统竖向位移自由度,如图1所示。

mc-车体质量(kg);α-车体点头自由度(°);z-车体竖向位移(mm);m1、m2、m3-车轮与悬架支撑系统质量(kg);z1、z2、z3-车轮与悬架支撑系统竖向位移(mm);ks1、ks2、ks3-悬架系统刚度系数(kN·m-1);cs1、cs2、cs3-悬架系统阻尼系数(kN·s·m-1);kt1、kt2、kt3-轮胎刚度系数(kN·m-1);ct1、ct2、ct3-轮胎阻尼系数(kN·s·m-1);ai(i=1～3)-第i个车轴与车辆质心水平距离(mm);lu-车辆前轴与后轴间水平距离(m)。

根据虚功原理[8],建立车辆动力学方程:

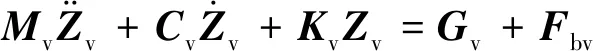
(1)

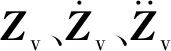
1.3 桥梁动力学方程

基于模态叠加法相关理论[9-10],建立桥梁动力学方程,如式(2)所示:

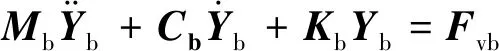
(2)

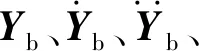
1.4 车-桥相互作用

将车辆和桥梁结构视为两个独立体系,两个体系通过轮胎和桥面之间的接触耦合联合起来,则车辆与桥梁间相互作用力Fti：

(3)

式中:ui为第i个轮胎与桥梁接触点处竖向位移,mm。

2 桥面不平度

桥面不平度为桥面偏离理想平面的程度。本文采用三角级数叠加法数值模拟桥面不平度[11],其相关公式如下所示:

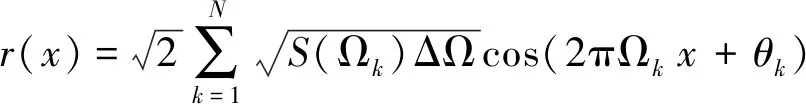
(4)

式中:r(x)为桥面不平度样本值,m;S(Ωk)为谱密度函数,m/cycle;Ωk为空间频率,cycle/m;ΔΩ为频率带宽,cycle/m;k为随机相位;N为采样频段。

通过调研,建立3种典型桥面不平度样本曲线(A、B、C级),如图2所示。

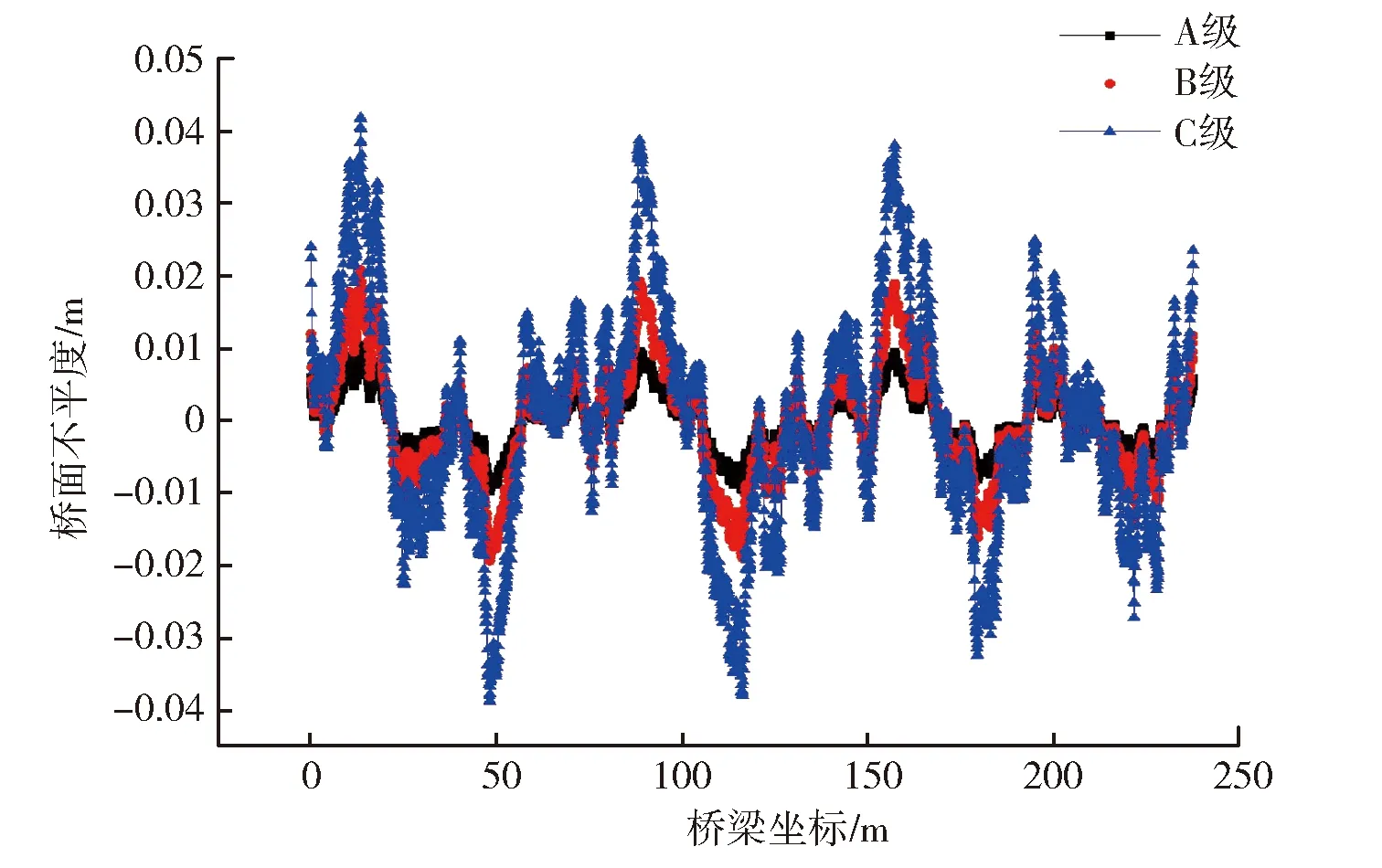
图2 典型桥面不平度曲线

3 工程简介

以三跨单箱单室截面的大跨弯连续刚构桥为工程实例,其中桥梁跨径组合为(65+108+65)m,曲率半径R=960 m,相关尺寸如图3所示。

(a) 立面图

4 不同敏感参数下桥梁冲击系数计算研究

冲击系数作为评价车桥动力响应的关键指标,十分重要。

4.1 冲击系数定义

4.1.1理论法

当采用理论法[12]进行桥梁冲击系数计算分析时,其计算公式如(5)所示:

μ=1-Ydmax/Yjmax

(5)

式中:μ为桥梁冲击系数;Ydmax为桥梁动力效应最大取值;Yjmax为桥梁静力效应最大取值。

4.1.2规范法

当采用规范法[13]计算冲击系数时,计算公式如(6)所示:

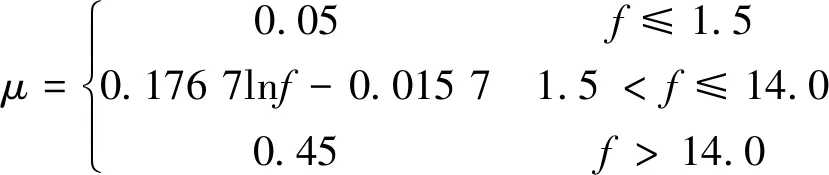
(6)

式中:f为桥梁基频,Hz。

4.2 敏感参数的确定

大跨弯连续刚构桥受多个敏感参数的共同影响,动力响应较为显著,本文选取曲率半径和桥面不平度两个敏感因素进行分析,其中车辆相关参数取值[14]如表1所示。

表1 车辆技术参数指标

本文选取曲率半径分别为R=250 m、R=500 m、R=750 m和R=960 m共4种桥型,桥面不平度分别为A级、B级、C级3个等级,通过单一参数法分别分析敏感参数对桥梁关键位置结构冲击系数的影响。

4.3 桥梁冲击系数影响研究

4.3.1曲率半径的影响

通过ANSYS软件的APDL二次开发,编写车桥耦合分析系统,模拟三轴车辆以车速v=60 km/h行驶并分别通过曲率半径R=250 m、R=500 m、R=750 m和R=960 m共4种桥型时,分析桥梁关键截面的冲击系数影响,结果如图4所示。

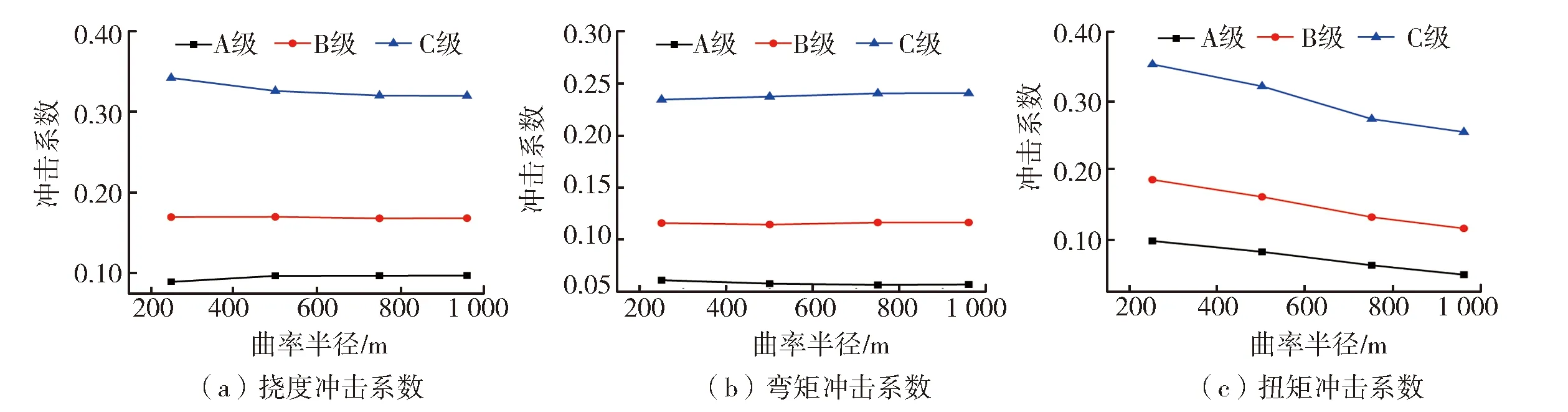
图4 桥梁冲击系数随曲率半径变化曲线图

结果表明:挠度、弯矩、扭矩冲击系数,均呈现在桥面不平度为C级最大,B级次之,A级最小,见图4(a)、(b)、(c);且随曲率半径的减小,结构的挠度和弯矩冲击系数较为平稳,变化幅度相对较小,表明曲率半径变化对结构挠度和弯矩冲击系数的影响较小,见图4(a)、(b);扭矩冲击系数随曲率半径的增大而减小,而当曲率半径R≤750 m时,扭矩冲击系数的变化随曲率半径的变化更为明显,且呈现为随曲率半径的减小即桥梁弯曲程度的增大,其扭矩冲击系数逐渐增大,见图4(c)。

4.3.2桥面不平度的影响

当车辆以车速v=60 km/h行驶通过不同等级桥面不平度的桥梁时,分析桥梁关键截面的冲击系数情况,结果如图5所示。

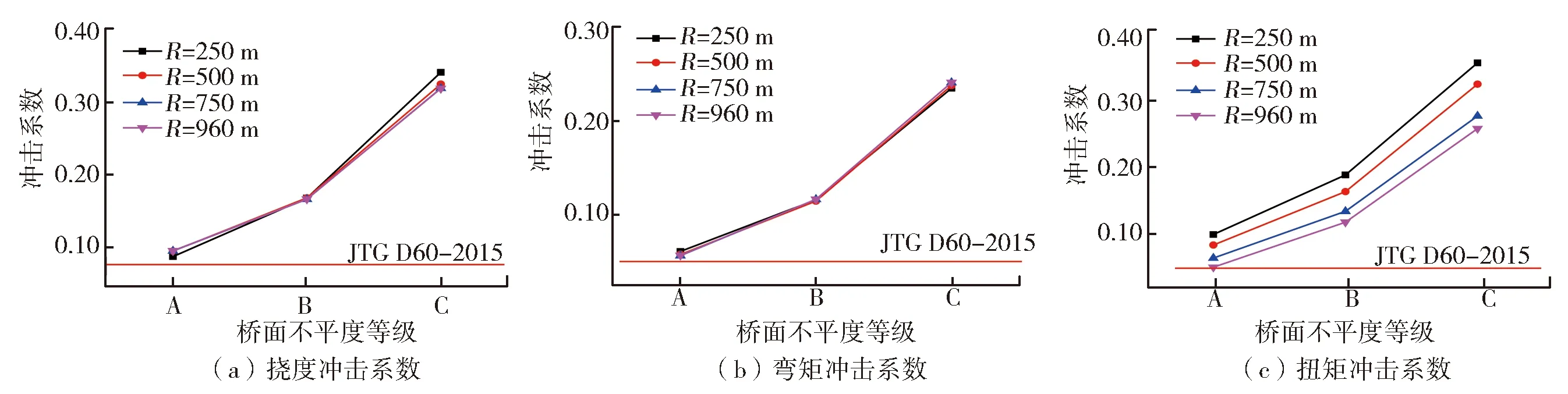
图5 冲击系数随不平整度变化曲线图

结果表明:随着桥面状况恶化,桥梁结构冲击系数整体有较大增幅,均超过了桥梁规范取值,尤其当桥面不平度处于B级和C级时,远超桥梁规范取值,说明现有规范在桥面状况较差时,此类桥梁冲击系数取值不太安全,建议在后续规范修订时考虑该因素的影响。

5 结论

1)通过模态综合法相关理论,分别建立车辆和桥梁的动力方程,通过车轮与桥梁的耦合关系,理论推导了引起桥梁动力响应的瞬时耦合荷载向量的计算公式,并采用三跨弯连续刚构桥工程实例,通过ANSYS中APDL二次开发,验证了方法的适用性。

2)基于车桥耦合理论,选取三轴平面车型为例,采用单一参数法研究了曲率半径和路面不平度对桥梁冲击系数的影响。结果表明:曲率半径变化对结构挠度和弯矩冲击系数的影响相对较小,对扭矩冲击系数的影响较为明显,即随着曲率半径的减小而增大;而随着桥面不平度变化时,各个指标的冲击系数取值有较大变化,随着桥面恶化呈增大趋势,尤其是B级和C级桥面下,冲击系数取值均远超规范取值。