An effective method to calculate the electron impact excitation cross sections of helium from ground state to a final channel in the whole energy region

Rui Sun(孙瑞), De-Ling Zeng(曾德灵), Rui Jin(金锐),Xiao-Ying Han(韩小英), Xiang Gao(高翔),‡, and Jia-Ming Li(李家明)

1Key Laboratory for Laser Plasmas,Ministry of Education,School of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China

2Collaborative Innovation Center of IFSA,Shanghai Jiao Tong University,Shanghai 200240,China

3Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

4Institute of Electron&Electronic Measurement Technology,Shanghai Institute of Measurement and Testing Technology,Shanghai 201203,China 5Max-Planck-Institut f¨ur Kernphysik Saupfercheckweg 169117,Heidelberg,German

6Department of Physics and Center for Atomic and Molecular Nanosciences,Tsinghua University,Beijing 100084,China

Keywords: the electron impact excitation cross sections, correction function, helium, the partial wave Rmatrix plus the first Born approximation method

1.Introduction

Electron impact excitation (EIE) cross sections of an atom/ion in a wide energy range(i.e.,from thresholds to above 10× thresholds) are indispensable physical parameters in astrophysics studies,inertial confinement fusion researches and so on.For example,helium is an abundant element in the universe.Accurate and reliable helium abundances are needed to calculate the primordial helium abundance by unit massYp,which is important for the study of cosmology and the chemical evolution of galaxies.[1–3]To obtain the helium abundance in astrophysics studies, one needs to estimate the contribution to the He I line intensities due to the collisional excitation, where the accurate EIE cross sections are essential.[4,5]Clegg showed for a sample of planetary nebulae (PNs) that the collision-to-recombination (C/R) correction (strongly dependent on the EIE cross sections)lowered the calculated He abundances by an average value of 10%.[4]

Many experimental studies[6–8]and theoretical calculations[9–14]have been carried out to investigate the EIE cross sections of He in the last decades.However, most of the calculations focus on a specific energy region (either on low or high energy region).The studies of EIE cross sections in the whole energy region are very limited.Fursa and Bray applied the convergent close-coupling(CCC)method to calculate e+He scattering cross sections excited from the ground state in the incident energy range from 1.5 eV to 500 eV,[13]

where the overall agreement with the experimental data is good, but without detailed resonance structures.It will also take large computational efforts for the CCC method to exhibit the cross sections in the whole energy region because it can only concentrate on a single energy at a time.It is known that,in the low incident energy region,the EIE cross sections with complex resonant structures near thresholds can be accurately calculated by the partial wave expansion method such asR-matrix method.[15–17]In the high incident energy region,the first Born approximation(FBA)is applicable and the EIE cross sections can be obtained from the generalized oscillator strengths(GOS).[18–22]Note that the quality of the target state wavefunctions is crucial for both partial wave expansion and GOS calculations.[14,18]Therefore, to calculate the EIE cross sections in the whole energy region efficiently,different methods should be used for different energy regions.[21]We have demonstrated for the e + He collision processes that the EIE cross sections of partial waveR-matrix method calculations can interface with the Born cross sections.[21]

In the present work, we propose an effective method to conveniently calculate the EIE cross sections with enough accuracy in the whole energy region.The e+He collision processes are used as an illustration example to show the validity and efficiency of our method.To facilitate the discussion,we will focus on the spin-allowed transitions.Because the spin-forbidden transitions are caused by the exchange interaction, then the FBA calculation should involve the matrix elements between the bound target electron and the scattering plane wave,[23,24]which makes these transitions usually less important in the high energy region[22]and would induce other complexity such as the non-orthogonality problem.[25]Considering the computational efforts are very large to use theR-matrix method alone below the FBA calculation region,we extend the calculation scheme presented in Ref.[21]by using the distorted wave (DW) approximation[26,27]calculations in the intermediate energy region between theR-matrix calculation region and FBA calculation region.The application of the DW method makes the interface of the EIE cross sections between different energy regions more effective.The accurate EIE cross sections of optical forbidden 11S–n1S (n=2–4)and optical allowed 11S–n1P(n=2–4)transitions are calculated using our extended scheme,which are in good agreement with the available experimental measurements.[28–32]Based on these accurate cross sections, we find that the ratios between these cross sections and the Born cross sections are nearly the same for different excitation final states belonging to the same channel.Then a universal correction function(CF)is proposed[16]and given to calculate the accurate EIE cross sections in the whole energy region with the same computational efforts of the Born cross sections,which may satisfy the needs in the related application fields.

2.Theory

To obtain the EIE cross sections of an atom/ion in the whole energy region from low to high, one should use different methods in the corresponding energy region.At low energy region, the interactions between the colliding electron and the target electrons involve electron exchange and correlation interactions, which is a many-body problem.The partial wave expansion method such asR-matrix method[15–17,34]is good to deal with these problems.At high incident energy region,the first Born approximation(FBA)is applicable[22,35–40]and various cross sections can be readily calculated as a whole instead of partial wave expansion.At the intermediate energy region,the distorted wave calculation can be applied,making the interface of EIE cross sections from low to high more effective.These three methods are all well-established methods detailed in many references.[22,27,34,35,41–43]Only some useful formulas are reviewed here for the sake of our following discussions.

The scattering matricesSis related to the transition matricesTby

The total cross sections from theR-matrix method for excitation from target stateito target statejin LS coupling is given from theTmatrices by[34]

HereNrepresents the number of all relevant partial waves,L,Sandπare the total orbital angular momenta,spin angular momentum and parity,respectively.[L]=(2L+1),[S]=(2S+1),landk2are the channel angular momenta and energies.σLis the corresponding partial cross section.

In high energy region, the FBA is valid and the incident and scattered electrons can be treated as plane waves.Within the FBA,the generalized oscillator strength(GOS)is defined as[22,35–39]

where ∆Eis the energy transfer(i.e.,excitation energy).Kis the momentum transfer related to the scattering angle.ΦiandΦjare the wavefunctions of the target atom for the initial and final states, respectively.rαrepresents the coordinate of theαth target electron,the coordinate origin is the center of mass of the target.

The differential cross section(DCS)is proportional to the GOS as

Thekandk′are the scattered electron momentums of the initial and final states, respectively.After performing the summation of the final state and the average of the initial state,we can obtain the FBA total cross section as

3.Computational results

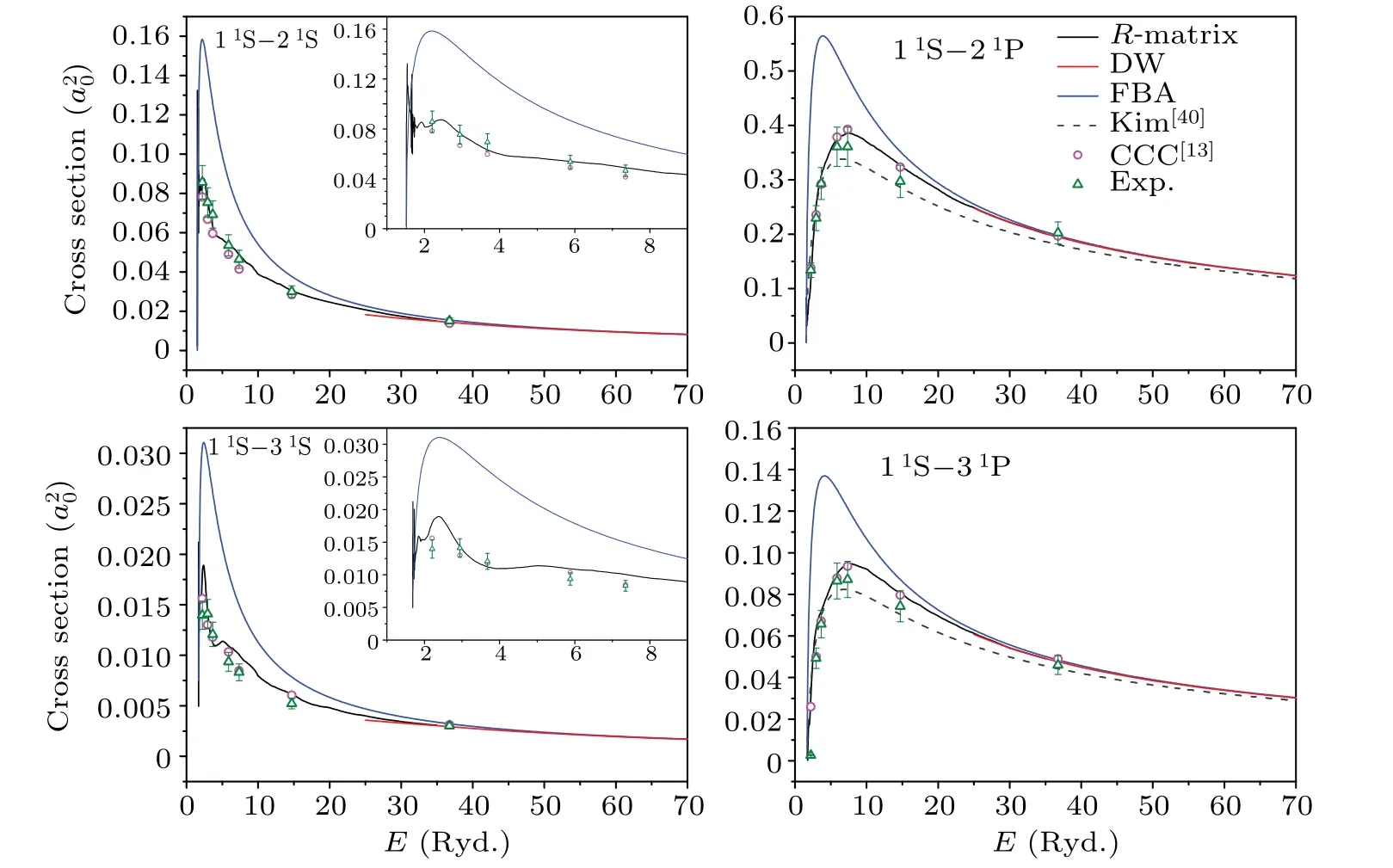
Fig.1.Our calculated EIE cross sections for the 11S–n1S (n=2, 3) and 11S–n1P (n=2, 3) transitions, and the comparison with other calculations[13,40] and experimental measurements.[28–32]

The corresponding coefficientsC1,T1,C2,T2,C3,T3in the formula are shown in Table 3.With these coefficients,the CF curve is well reproduced as shown in Fig.2(b).

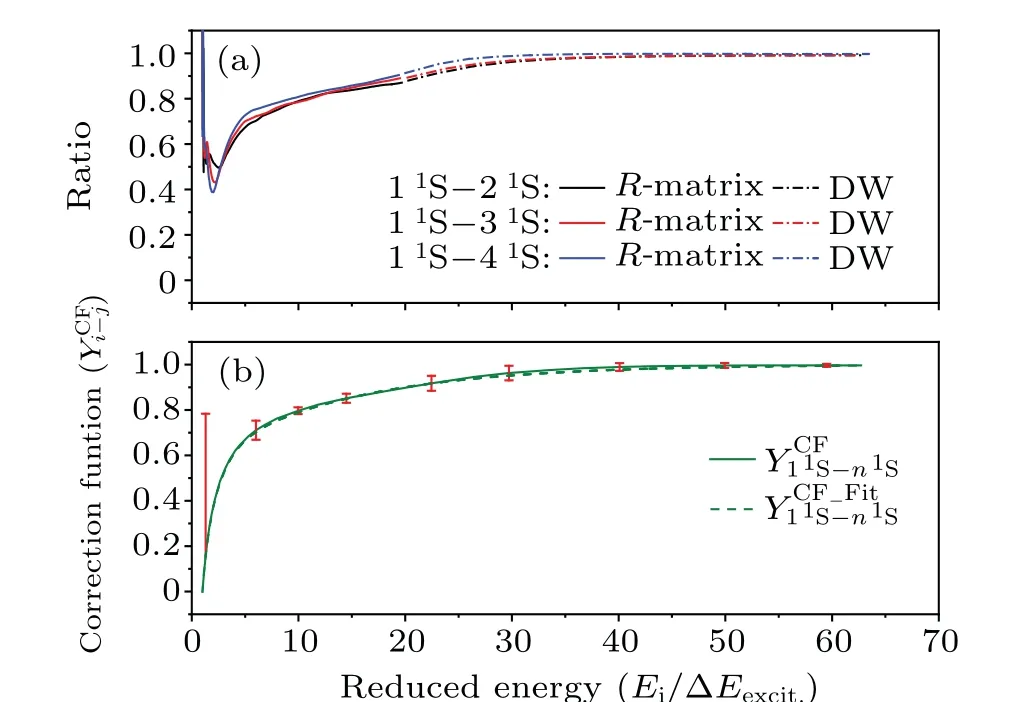
Fig.2.(a) Ratios (accurate total cross sections over the total FBA cross sections) for 11S–21S, 11S–31S and 11S–41S transitions.The colored solid lines are ratios for R-matrix calculations, i.e.,σ(R-matrix)total /.The colored dash lines are ratios for DW calculation, i.e., /.(b) Correction functions for [1s2] 11S–[1sns] n1S transitions and corresponding analytical curve Correction function for 11S–n1S is obtained by summarizing the ratios in (a).Reduced energy is the ratio between the incident energy Ei and the transition excitation energy Eexcit.

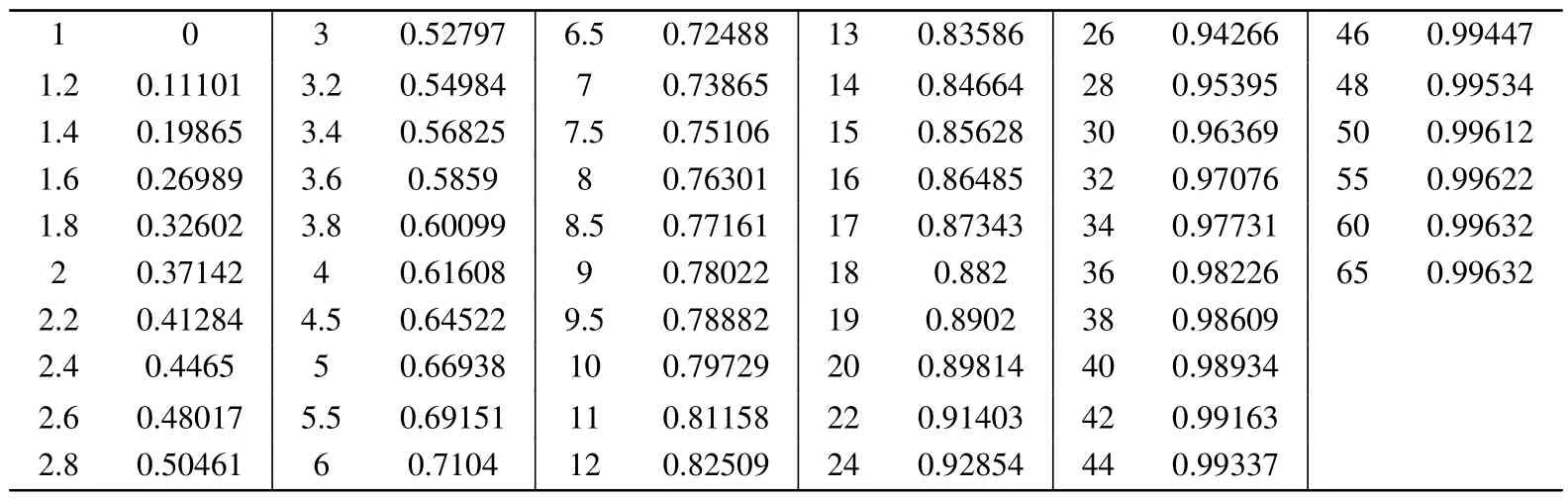
Table 1.Correction function data for[1s2]11S-[1sns]n1S transitions.

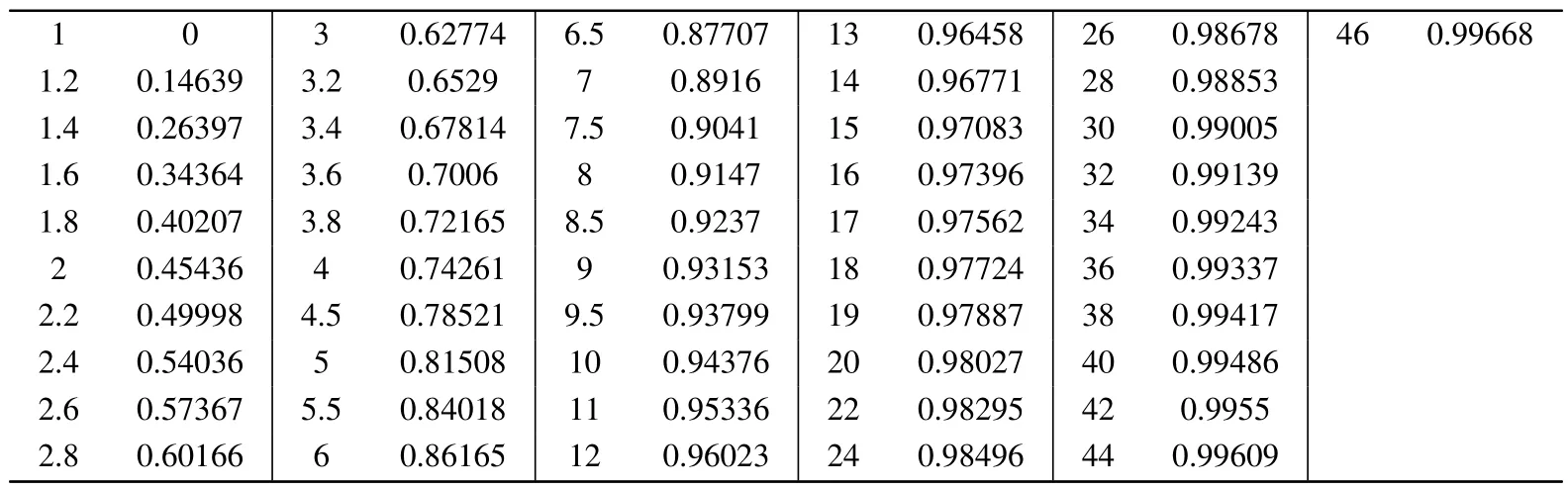
Table 2.Correction function data for[1s2]11S-[1snp]n1P transitions.

Table 3.The coeffciients of the analytical formulasfor the correction functions(a(b)represent a×10b).

Table 3.The coeffciients of the analytical formulasfor the correction functions(a(b)represent a×10b).

i-j 11S–n1S 11S–n1P C1 4.39(-1) 5.37(0)T1 1.35(1) 3.05(–1)C2 9.44(–1) 1.12(0)T2 1.48(0) 2.30(0)C3 1.47(0) 8.00(–2)T3 3.89(–1) 1.39(1)

Figure 3(a) shows the ratios of accurate total cross sections and total FBA cross sections of our calculations for 11S–n1P (n=2–4) transitions in reduced incident energies.The ratios forR-matrix calculation naturally interface with the corresponding ratios for DW calculation at around the reduced energy about 15 for all the 3 11S–n1P (n=2–4) transitions.Similar to the 11S–n1S transitions,there exist resonant structures in the low reduced energy region.While in the high energy region,the ratios for DW calculation gradually merge to 1,which means the cross sections calculated by distorted wave method are equal to those by FBA.The ratios of Kim’s scaled cross sections[40]are also displayed.Compared to our ratios,

Fig.3.(a) Ratios (accurate total cross sections over the total FBA cross sections) for 11S–21P, 11S–31P and 11S–41P transitions.The colored solid lines are ratios for R-matrix calculations, i.e.,σ(R-matrix)total /.The colored dash lines are ratios for DW calculation, i.e., /.(b) Correction functions for [1s2] 11S–[1snp]–n1P transitions and corresponding analytical curve.Correction function for 11S–n1P is obtained by summarizing the ratios in(a).Reduced energy is the ratio between incident energy Ei and the transition excitation energy Eexcit.

4.Discussion and conclusion

Finally,we would like to conclude with the following remarks.With our proposed effective method to calculate the EIE cross sections with enough accuracy in the whole energy region by combination ofR-matrix method, DW method and FBA methods in the low,intermediate and high energy regions respectively,accurate e+He collisional excitation cross sections from the ground state to the finaln1S(n=2–4)andn1P(n=2–4) states are calculated, which are in good agreement with the available experiments.[28–32]By studying the ratios(accurate total cross sections over Born cross sections)within the same channel, we find that these ratios have similar behaviors and are close to each other, which means they have the same channel properties.Although the calculated ratios in Figs.2(a) and 3(a) do not show strict convergent behavior, it is interesting to note that the channel property of these ratios in the high energy region is understandable from the analysis of the related cross sections.More specifically,the ratio in the high energy region could be calculated as the ratio between the DW cross section and FBA cross section.As shown in Ref.[44]for the DW electron impact excitation cross sections and Eq.(5) for those FBA cross sections, both cross sections can be factorized as a one-body matrix element defined only on the involved target states and a smooth function of the excitation energy.The channel property of the first part stems from the channel property of the excited target wavefunctions,[45,46]whereas that of the second part stems from the fact that the change in the excitation energy would be smaller and smaller when the excitation degree increases (the excitation energy would ultimately converge to the ionization energy).Based on this argument, we expect the channel property in our defined ratio would be a universal one in general atomic systems.Therefore we propose a universal correction function(CF)YCFi-jbased on these properties for the calculation of all highly excited final states in the same channel.By utilizing the correction function, one can conveniently obtain the EIE cross sections of any transition in the same excitation channel in the whole energy region based on the Born cross sections.The CF is a smooth curve with error bars in different energy regions,which should be convenient for one to estimate the accuracy of the calculated cross sections.In our case,the largest error bars are in the low energy region due to various resonant structures.For applications sensitive to the precisions of EIE cross sections in that region, a direct usage of theR-matrix calculation results is preferred.The CF for He EIE cross sections from the ground state to the final n1S and –n1P states with arbitrarynare provided as shown in Tables 1 and 2(also Ref.[33]for a fortran subroutine in the supplementary materials in PDF format),as well as the fitting formula Eq.(10)with the corresponding coefficients shown in Table 3.In this way,the accurate EIE cross section can be acquired by the formula) for the transitionsi-j(11S–n1S and 11S–n1P).

Note that although some empirical quasi-universal scaling factors to correct the first Born cross sections have been proposed,[40,47–50]they are not applicable in general cases and with limited accuracies.For instance,Tian and Li[48]proposed a correction function by which one can obtain the spin-allowed EIE cross sections from FBA cross sections with an accuracy of about 50%.Kim introduced a correction using three atomic properties (i.e., the ionization energy, the excitation energy and the dipolefvalue)to improve the plane-wave Born cross sections for electron-impact excitation of neutral atoms[40]and singly charged ions[50]for spin and electric dipole-allowed transitions with an accuracy of about 20%.On the other hand,the universal correction functions we proposed can not only apply to spin-allowed transitions, which have been shown in the present work, but also to the spin-forbidden transitions.Because they are obtained from the ratios of the calculated accurate cross sections and the readily obtained approximated cross sections, which should be very flexible.In addition to neutral atoms, our proposed correction functions should be also valid for various degrees of ionized atoms by considering the Elwert factor at the thresholds.[51]Furthermore, the calculations from the ground state to the final channels in the present work can be extended to the case of any excited states to final channels,[18]and even for the case of any initial channels to any final channels,[52]which could be very useful in providing precise total cross sections in the whole energy region for many research fields,such as astrophysics studies and inertial confinement fusion research.

Data availability statement

The data that support the findings of this study are openly available in Science Data Bank at https://doi.org/10.57760/sciencedb.j00113.00142.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.12241410).