Algebraic form and analysis of SIR epidemic dynamics over probabilistic dynamic networks

Hongxing Yuan·Zengqiang Chen·Zhipeng Zhang·Rui Zhu·Zhongxin Liu

Abstract The outbreak of corona virus disease 2019 has profoundly affected people’s way of life.It is increasingly necessary to investigate epidemics over social networks.This paper studies susceptible-infected-removed(SIR)epidemics via the semitensor product.First,a formal susceptible-infected-removed epidemic dynamic model over probabilistic dynamic networks(SIRED-PDN)is given.Based on an evolutionary rule,the algebraic form for the dynamics of individual states and network topologies is given,respectively.Second,the SIRED-PDN can be described by a probabilistic mix-valued logical network.After providing an algorithm,all possible final spreading equilibria can be obtained for any given initial epidemic state and network topology by seeking attractors of the network.And the shortest time for all possible initial epidemic state and network topology profiles to evolve to the final spreading equilibria can be obtained by seeking the transient time of the network.Finally,an illustrative example is given to show the effectiveness of our model.

Keywords SIR epidemic·Probabilistic dynamic networks·Final spreading equilibria·Semi-tensor product of matrices·Algebraic form

1 Introduction

The outbreak of corona virus disease 2019 (COVID-19)has profoundly affected people’s way of life.In fact, every outbreak of epidemics has seriously affected people’s production, life and even lives.Therefore, people have been studying epidemics since ancient times.The classical differential equation epidemic models are presented to describe the spreading process of the epidemic, analyze the number of infected people and explore means to stop the spread of epidemic[1,2].However,these classical models do not take the evolution of spreading networks into account, that is,spreading networks of these models are static.

In real life, if a susceptible individual realize that their neighbors are infected, he or she is likely to disconnect from these neighbors and establish neighbor relationships with other susceptible individuals rather than infected individuals.That is to say, with the evolution of an epidemic,spreading network is always dynamic.Therefore, it is very practical and necessary to study epidemics whose spreading networks are dynamic.Most scholars use computer simulation and statistics[3–6]to study these epidemics.Recently,[7] has put forward a new type of matrix product called the semi-tensor product(STP)of matrices which has shown its superiority in many fields,including finite automata [8–10],games[11–13],networked evolutionary games[14–16],logical networks [17–25], etc.Logical networks are classified as deterministic and probabilistic [7].So we define that a dynamic network is deterministic,if its every network is deterministic.A dynamic network is probabilistic, if it contains a probabilistic network.If not specified, dynamic networks refer to deterministic dynamic networks.Based on theSTP,Guoetal.[26,27]establishedasusceptible-infectedsusceptible epidemic dynamic model over dynamic networks(SISED-DN), providing a method for mathematically analyzing epidemics with deterministic dynamic networks.In SISED-DN,the spreading networks are deterministic,rather than probabilistic, so probabilistic events in the spread of epidemics cannot be fully described.

Compared to the SIS epidemics model, the SIR epidemics model has a wider range of applications and has more research value [28–30].For example, the outbreak of COVID-19 at the end of 2019 can be analyzed by establishing a SIR epidemic dynamic model.That is because for the epidemic with highly infectious,infected individuals are more likely to become immune or dead,rather than becoming susceptible again.To our knowledge,most of the research results on SIR epidemics whose spreading networks are dynamic are obtained by computer simulation[31]and mean-field method[3,32].The computer simulation method can not fully study the probabilistic events in the spread of epidemics, and it is difficult to find the shortest time and all possible final spreading equilibria, which are key global information in the analysis of epidemics.The mean-field method can only reflect the average trend of the spread of epidemics.So we would like to solve the above problems by using the semitensor product of matrices.

Motivated by the above, we use the STP to establish a susceptible-infected-removed epidemic dynamic model over probabilistic dynamic networks(SIRED-PDN)which can be described by probabilistic mix-valued logical networks.The number of each node’s possible states is finite.The main contributions of this paper are as follows:

• A formal SIRED-PDN is provided and the algebraic form for the dynamics of individual states and network topologies is given,respectively.

• All possible final spreading equilibria and the shortest time for all possible initial epidemic state and network topology profiles to evolve to the final spreading equilibria can be obtained by the algorithm given in this paper.

• An illustrative example is given to show the effectiveness of our model.One can check the result of the example with the help of MATLAB toolbox.

The rest of this paper is arranged as follows.Section2 introducessomepreliminariesabouttheSTP.Section3establishes the algebraic form of the SIRED-PDN.Section4 gives two algorithms and analyzes the SIRED-PDN by calculating the final spreading equilibria and the shortest time.An illustrative example is also given in Sect.4.Section5 gives a brief conclusion.

2 Preliminaries

2.1 Notations

2.2 Semi-tensor product of matrices

In this section, we introduce some necessary preliminaries about the semi-tensor product.One can refer to[7].

Definition 1 [7] LetY∈Mu×v,Z∈Mk×t, andc=lcm(v,k) (the least common multiple ofvandk).Define the semi-tensor product(STP)ofYandZas

where“⊗”is Kronecher product.

Whenv=k,Y⋉Z=Y Z,so we will omit“⋉”hereafter.

Proposition 1 [7]

(1)For any Y∈Mu×1,A∈Mk×t,we have

(2)Let Y∈Mu×1and Z∈Mv×1.Then

where W[u,v]∈Muv×uv denotes the swap matrix,

(3)Assume Y∈Δu,then we get

where

stands for the order reducing matrix.(4)For any Y∈Δu,Z∈Δv,we have

whereis the rear(front)deleting operator.

(5)Let yi∈Δu,i= 1,2,...,n and y=,then we get

where

Definition 2 [7] Define the Khatri-Rao product ofA∈Ma×candB∈Mb×cas

Proposition 2 [7]

(1)Assume g:Dnu→Du is a u-valued logical function which is represented by

Identify i∼δiu,i= 1,2,...,u.Then there exists a unique logical matrix Mg∈Lu×un which we call the structure matrix of g.The algebraic form of(7)is

where y,xi∈Δu,i=1,...,n.

(2)If in item(1)Δu is changed to Υu,the result remains true except that the structure matrix Mg∈Lu×un in(8)is changed to a Mg∈Υu×un.

3 Algebraic form of SIR epidemic dynamics over probabilistic dynamic networks

In this section,by using the STP,the algebraic form of SIR epidemic dynamics over probabilistic dynamic networks is given.In Sect.3.1,a formal SIRED-PDN is provided.Sections3.2and3.3calculatethealgebraicformforthedynamics of individual states and network topologies,respectively.

3.1 SIR epidemic dynamic model over probabilistic dynamic networks

This part presents a formal SIRED-PDN,it consists of four basic components:

(1)nindividuals,whose states are susceptible(S),infected(I)orremoved(R).xi(t)∈{S,I,R}standsforthestate of individualiat timet.“xi(t)=2”indicates the state of individualiat timetis “I”, “xi(t) = 1” indicates the state of individualiat timetis“S”and“xi(t)=0”indicates the state of individualiat timetis“R”.N={1,2,...,n}represents the set of individuals.

(2) An undirected graphG=(N,ε(t))stands for a timevarying network topology,whereε(t) = {(i,j)|i,j∈N,i/=j} represents the social connections between pairs of individuals.The adjacent matrix ofGat timetis

(3) The dynamics of individual states: In each period,susceptible individuals have a certain probability of becoming infected due to social connections with their infected neighbors.Infected individuals have a certain probability of becoming removed.Removed individuals are dead or have a strong immunity,so they will not become infected any more.

(4) The dynamics of network topologies:For each SI connection(connection between an infected individual and a susceptible individual),the susceptible individual has a certain probability of breaking this SI connection,and establishing a new connection with a susceptible or removed individual who do not have a social connection with this susceptible individual.Every susceptible individual breaks at most one connection in each period to avoid repeated connections.

Based on the above,the dynamics of individual states and network topologies is represented by

whereX(t) =(x1(t),x2(t),...,xn(t)) stands for the state of all individuals at timet,E(t)is defined as(9),PandQare evolutionary functions of individual states and network topologies,respectively.

3.2 Algebraic form for the dynamics of individual states

Thispartgivesthealgebraicformforthedynamicsofindividual states via the STP approach.We first present the dynamics of individual states.

In each period,each susceptible individual is infected by each of its infected neighbors with the probabilityβ, each infected individual is cured or dead from the epidemic with the probabilityα,becoming removed.

To give the algebraic form of SIR epidemic dynamics over probabilistic dynamic networks,we express individual states and network topologies into vector form.

For each kind of individual state,we identify the infected stateI∼δ13,the susceptible stateS∼δ23and the removed stateR∼δ33, then {S,I,R} ∼Δ3can be obtained.Considering probability of the epidemic, letxi(t+ 1) ∈Υ3.xi(t+1) = [r1,r2,r3]′indicates the state of individualiat timetis infected with probabilityr1,susceptible with probabilityr2,removed with probabilityr3.

For each kind of network topology, because its adjacent matrixEsatisfiesei j=e jiandeii= 0,Ecan be uniquely determined by itsupper triangular elements.Therefore we can express the network topology as(c1,c2,...,cq) :=(e12,...,e1n,...,ei,i+1,...,ei,n),whereca(i,j)(t)=ei j(t),

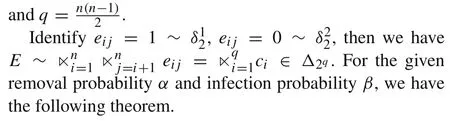
Theorem 1In a formal SIRED-PDN,the algebraic form of individual states’dynamics is calculated by

ProofFor the given removal probabilityαand infection probabilityβ, when the state of individualiat timetis infected,the state of individualiat timet+1 will become removed with the probabilityαand retain infected with the probability 1-α.When the state of individualiat timetis susceptible, the state of individualiat timet+ 1 will become infected with the probability 1 -(1-β)bi(t)and retain susceptible with the probability(1-β)bi(t), wherebi(t)denotes the number of individuali’s infected neighbors at timet.When the state of individualiat timetis removed,the state of individualiat timet+1 will retain removed with the probability 1.Combining with the vector form of the individual state,we have

whereT(β) =(1-(1-β)bi(t),(1-β)bi(t),0)′,H(α) =(1-α,0,α)′.

For the process of removal,we have

Therefore,Eq.(15)can be converted into

Multiplying all equations together yields Eq.(13).It is the algebraic form of (10),based on which we can analyze the dynamics of individual states.■

3.3 Algebraic form for the dynamics of network topologies

This part gives the algebraic form for the dynamics of network topologies via the STP approach.We first present the dynamics of network topologies.

In each period, each SI connection (connection between an infected individual and a susceptible individual) breaks with the probabilityw.When it breaks,the susceptible individual in this SI will randomly establish a new connection with a susceptible or removed individual who do not have a social connection with this susceptible individual,if such an individual exists.Every susceptible individual breaks at most one connection in each period to avoid repeated connections.Therefore we can get the following theorem.

Theorem 2In a formal SIRED-PDN,the algebraic form of network topologies’dynamics is calculated by

For each connection(iz,jz) in ¯Ju,v, we denote the state of(iz,jz)at timet+1 byaz.az=(1,0)′denotes breaking this connection at timet+1,it happens with the probabilityw.If this connection breaks,the increment ofuwill be

4 Analysis of SIR epidemic dynamics over probabilistic dynamic networks

Substituting(13)into(17)yields

Therefore,the algebraic form of(10)and(11)is

Multiplying the above two equations together yields

Denote

whereL=L′Q∗L P,Y(t)=E(t)X(t).

In the previous content,we hadX(t)∈Δ3n,E(t)∈Δ2q,X(t+1)∈Υ3n,E(t+1)∈Υ2q,which may be a little confused,so we give the following explanation.To simplify,we use profile to stand for epidemic state and network topology profileY(t)hereafter.Epidemics are usually studied for prediction purposes,thus the profile at this moment is generally deterministic rather than probabilistic.So we definedX(t) ∈Δ3n,E(t) ∈Δ2q.In practice,the infection probability and removal probability are generally used to describe an epidemic, thus the predicted profile at the next moment is uncertain.So it makes more sense to represent a predicted profile with a probability vector, that is,X(t+1) ∈Υ3n,E(t+1)∈Υ2q.

Through Eq.(19), we can see that the structure matrixLcontains each deterministic profile’s next moment profile.We can multiply each deterministic profile’s next moment profile by the probability of the deterministic profile occurring,then put them together to get the next moment profile of a probabilistic profile.This operation can be easily accomplished by taking the STP ofLwith this probabilistic profile.Therefore, although Eq.(19) is obtained under the premise that all profiles at this moment are deterministic,it still holds when the profile at this moment is probabilistic according to the meaning of taking the STP.

To sum up,all information about the SIR epidemic dynamics over probabilistic dynamic networks can be obtained by analysing the probabilistic matrixLwhose detailed calculation process is in Algorithm 1.

Algorithm 1 The algebraic form of the SIRED-PDN for each integer i ∈[1,n]do Calculate Li =images/BZ_120_1570_919_1584_954.pngMH MT δ33 ⊗1′2q·3nimages/BZ_120_1862_919_1876_954.pngW[2q·3i-1,3](I2q·3i-1 ⊗O3)end for Calculate the structure matrix of X(t +1)=L P E(t)X(t) as L P =L1 ∗···∗Ln.for each integer u ∈[1,2q]do for each integer v ∈[1,3n]do if | ¯Ju,v|≥1 then Calculate Col(u-1)2n+v(L Q)=2| ¯Ju,v|images/BZ_120_1357_1292_1394_1327.png| ¯Ju,v|Π t=1 z=1([w1-w]az)·δu′2q.else Calculate Col(u-1)2n+v(L Q)=δu2q.end if end for end for Calculate the structure matrix of E(t +1)=L′Q E(t)X(t) as L′Q =L Q(I2q ⊗L P)O2q.Calculate the structure matrix of E(t +1)X(t +1)= LE(t)X(t) as L = L′Q ∗L P.

The following two propositions provide the method of calculating attractors and the transient time for deterministic mix-valued logical networks.

Proposition 3 [7]

(1)For a mix-valued logical network,the number of cycles of length u,indicated by Au,is inductively determined by

where P(u)represents the set of u’s proper factors.Fixed points stand for the cycles of length1,and Ae expresses the number of fixed points.Attractors are composed of fixed points and cycles.

Proposition 4 [7]The transient time of a mix-valued logical network is indicated by

where u represents the number of all possible L.

BecauseLin our model is a probabilistic matrix,we cannot directly use the above two propositions.If we directly substituteLinto the above two propositions to calculate attractors and the transient time,there are two places that will not work properly,so we give the following two assumptions to approximate the probabilistic events as deterministic,thus we can get attractors and the transient time properly.

Assumption 1 When the probability of an event is greater than a given valuep,the event is an inevitable event.

Assumption 2 When the norm of the difference between two probability matrices is less than a given valuee, the two probability matrices are regarded as the same.

Remark 1There are many kinds of norms.For any norm,ereflects the degree of neglect of low probability events.In practice,wecanchoosearelativelylowe,suchas0.01,0.001.

According to the probabilistic mix-valued logical network(19) and Assumption 1, we defineM(k)as follows.Figure out all elements greater thanpin matrixLk.For each of these elements,we denote it as(Lk)s,t.Let Colt(Lk)=.We denoteLkafter these operations asM(k).

In accordance with the above approximation,we give the following definitions for attractors and the transient time of the probabilistic mix-valued logical network(19).

Definition 3 Under Assumptions 1 and 2, attractors which are composed of fixed points and cycles for the probabilistic mix-valued logical network(19)are defined as follows:

(1) IfM(1)Y0=Y0,Y0∈Δ2q·3n,thenY0is a fixed point.

(2) IfM(u)Y0=Y0andanytwoelementsinset{Y0,M(1)Y0,...,M(u-1)Y0} are distinct, then {Y0,M(1)Y0,...,M(u)Y0}is a cycle with lengthu.

Denote the limit set asΩ,which consists of all attractors.

Definition 4 Under Assumption 1 and 2,the transient time is the smallestksatisfying that for anyY0∈Δ2q·3n,M(k)Y0∈Ω.

Thedefinitionsoftheabovetwoconceptsfordeterministic networks can refer to[7].The differences between the definitions in probabilistic networks and deterministic networks are the descriptions about the inevitable event and matrix equality.The differences are the reason why Propositions 1 and 2 cannot be used on the probabilistic matrixLproperly.SowhenweapplyPropositions1and2onL,weshoulddothe following two approximations.We should replaceLkwithM(k),that is to say,the relatively high probability events in the probabilistic network should be approximately regarded as inevitable events.We should replaceA=Bwith that the norm ofA-Bis less thane, that is to say, the relatively low probability events in the probabilistic network should be approximately regarded as zero probability events.

Then we can obtain all attractors in the probabilistic mixvalued logical network,that is,final spreading equilibria of the SIR epidemic dynamics,where an equilibrium means that both individual state and network topology be stationary or change periodically.Meanwhile,we can obtain the transient time of the probabilistic mix-valued logical network,that is,the shortest time for all possible initial profiles to evolve to the final spreading equilibria of the SIR epidemic dynamics.The detailed calculation process is in Algorithm 2.

for each integer i ∈[1,r]do Let Z be the first matrix in cell LL, and delete it from the cell LL.for each integer j ∈[1,|LL|]do if the norm of Z -LL{j}is less than e then The transient time is i.Break.end if end for end for

Remark 2The computational complexity of any algorithm based on the STP of matrices is exponential[33].However,it is worth pointing out that most of the elements ofLin Eq.(18)are zeros,so it does not require a lot of storage space in the computer and the calculation speed is relatively fast.

Example 1There are three retailers in the market,and trade may occur between them.If some retailers are infected by an epidemic,others are likely to adjust their trade relations to avoid infection.In addition,retailers who suffer from this epidemic will develop immunity after being cured or die from the epidemic.If a retailer is cured or dead,he or she will not be infected again.

The above epidemic can be modeled as a SIRED-PDN,whereN= {1,2,3}.Next, we give the parameters in this example.In each period, each susceptible retailer is infected by each of his infected neighbors with the probabilityβ= 0.5, each infected retailer is cured or dead from the epidemic with the probabilityα= 0.6, becoming removed.Each SI connection breaks with the probabilityw= 0.4.When it breaks,the susceptible retailer in this SI will randomly establish a new connection with a susceptible or removed retailer who do not have a social connection with this susceptible retailer, if such an individual exists.Every susceptible individual breaks at most one connection in each period to avoid repeated connections.When the probability of an event is greater than a given valuep=0.78,the event is an inevitable event.When 2-norm of two probability matrices is less than a given valuee=0.001,the two probability matrices are regarded as the same.

whereL∈Υ216×216.

Through Algorithm 2,all final spreading equilibria and the transient time can be obtained.According to the calculation results,there are 64 final spreading equilibria,that is,whenE(t)X(t)takes these 64 values,the network will no longer change.In each final spreading equilibrium,three retailers’states areδ33orδ23,that is,RorS.This is in line with common sense.Because only when there is no infected retailer in network, the network will no longer change.According to the calculation results,the transient time is 10,which means that any initial network will evolve to an spreading equilibrium after at most 10 times of evolution,and will not change any more,as in Fig.1.

5 Conclusions

This paper gave a formal susceptible-infected-removed epidemic dynamic model over probabilistic dynamic networks(SIRED-PDN),then the algebraic form for the dynamics of individual states and network topologies was given using the STP.SIRED-PDN can be regarded as a probabilistic mixvalued logical network.When the probability of an event is greater than a given value, the event is considered as an inevitable event in this paper.Then all possible final spreading equilibria and the shortest time for all possible initial epidemic state and network topology profiles to evolve to the final spreading equilibria can be obtained.Two algorithms were given to show the detailed calculation process and an example was provided to verify the validity of our results.In conclusion,this paper provided a method for mathematically analyzing SIR epidemics whose spreading networks are dynamic,rather than using computer simulation and statistics methods.In the future,we would like to apply the semi-tensor product of matrices to more types of epidemics.

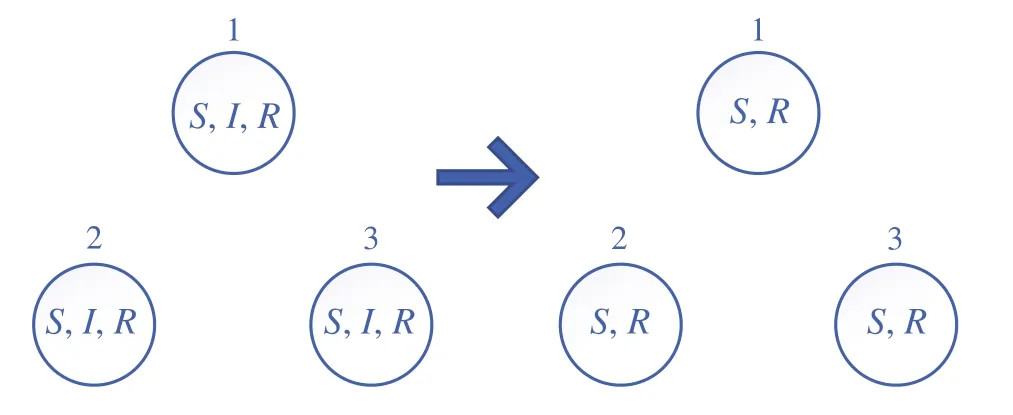
Fig.1 No matter how three retailers are connected and what three retailers’states are,every retailer’s state will evolve into susceptible or removed and no longer change after at most 10 times of evolution

Declarations

Conflict of interest The authors declare that there is no conflict of financial or non-financial interests that are directly or indirectly related to the publication of this paper.