Robust non-aggressive three-axis attitude control of spacecraft:dynamic sliding mode approach

Javad Nikyar·Farhad Bayat·MohammadAli Mohammadkhani

Abstract Conventional sliding mode control (SMC) has been extensively applied in controlling spacecrafts because of its appealing characteristics such as robustness and a simple design procedure.Several methods such as second-order sliding modes and discontinuous controllers are applied for the SMC implementation.However, the main problems of these methods are convergence and error tracking in a finite amount of time.This paper combines an improved dynamic sliding mode controller and model predictive controller for spacecrafts to solve the chattering phenomenon in traditional sliding mode control.To this aim,this paper develops dynamic sliding mode control for spacecraft’s applications to omit the chattering issue.The proposed approach shows robust attitude tracking by a set of reaction wheels and stabilizes the spacecraft subject to disturbances and uncertainties.The proposed method improves the performance of the SMC for spacecraft by avoiding chattering.A set of simulation results are provided that show the advantages and improvements of this approach (in some sense) compared to SMC approaches.

Keywords Dynamic sliding mode control·Attitude control·Model predictive control·Spacecrafts

1 Introduction

The design of attitude control systems for satellites has been considered widely during the past decades.Various methods of robust and optimal control design have been used because in uncertain situations, the satellite’s performance and achieving mission objectives can be significantly reduced.The developments on satellite can be split into three maincategories.Thetwofirstcategoriesincludeoptimalcontrol methods and the state feedback controllers[1].The third category applies data-driven techniques for stabilizing orbital or angular motion [2].Optimal open loop systems require an exact predetermined pointing which includes the solution of two-point boundary value problem, and research shows that there are no solutions for these problems of uncertain dynamical systems.Therefore,robust satellite attitude control system plays a vital role in the satellite’s performance,because a small error can decrease mission duration even for years which leads to a great cost[3].The sliding mode control in[4]and[5]for spacecraft pointing and regulation uses both a Rodrigues representation and a quaternion representation.Chattering and tracking error are most important factors of a robust sliding mode control technique.Xu et al.[6]considered the problem of controlling attitude and position states by applying a genetic algorithm-based optimization problem to get a better performance.During most of the flight time,Hui and Li[7]proposed terminal sliding mode control(TSMC) to reduce chattering.Different varieties of TSMC method are widely used in different applications[8,9].A disturbance observer is proposed in[10]to decrease chattering and improve the stability of the spacecraft platform.Secondorder sliding mode control(2-SMC)is an efficient method for especially second-order uncertain plants to reduce chattering and improving the performance.An asymptotic 2-SMC is proposed in[11]and used for satellite,and a Lyapunov function was applied to prove the asymptotic stability problem.Nair et al.[12] combined SMC technique and data-driven techniques for path planning to design a robust controller.They also applied a fuzzy controller to decrease the chattering inherent in the SMC.By using Lyapunov’s direct method to lessen the disturbance effects, Cao et al.[13]applied the integral sliding mode control method.Lee and Singh[14]considered the notion of geometric homogeneity and designed a higher-order SMC system which includes a nominal nonlinear finite-time-stabilizing control law.Kang et al.[15] proposesd a roust fractional order sliding mode control for the deployment of satellite with uncertainty of unknown disturbances.They have proposed fractional order sliding mode control includes two sub-sliding surfaces that are designed separately.The controller which is proposed in[15]produces a controller to make all states converge to the desired states.Finally, they compared the performance with the PD, fractional PD and sliding mode controller.In recent years, researchers have extended adaptive sliding mode control scheme by applying uncertainty and disturbanceestimatortoavoidchattering.Wangetal.[16]proposed adaptive terminal sliding mode control(ATSMC)technique that includes adaptation methodology for removing external disturbance effects.

While this paper extends a robust method for attitude control of spacecraft, it is well suited to use similar method systems in many industrial as well as civil engineering environments, in which safety and economical constraints are significant factors.Similar to satellite, a growing interest has arisen about the design of sliding mode controllers for container cranes.Event-triggered global sliding mode control (GSMC) is an interesting method for removing chattering and to upgrade the performance for stabilizing spacecraft.Zanjani and Mobayen [20] proved that GSMC minimizes communication resources and execution time,while it reaches the manifold and equilibrium point from any initial state in a limited time range.The main benefits of the GSMC are higher robustness against parameter variation and disturbances, eliminating the reaching phase of traditional sliding mode control,optimizing resources at the implementation phase and removing the Zeno phenomenon.Applying augmented disturbance observers and filters is another effective method to remove the chattering of the SCM industrially[21, 22].Sindhuja et al.[23] proposed a robust augmented derivative-free Kalman filter in association with sliding mode controller,which effectively removes the input disturbances and can be a basis for future research of this paper.

Fig.1 A satellite with appendages such as the solar panels and antennas

Unmodeled parameters, frictions and other uncertainties are significant factors for the control system of the spacecrafts.Spacecrafts are highly vulnerable to disturbances and uncertainties in space.The orbital spacecraft maneuvers are very challenging because of mass constraint uncertainties and payload complexity.For spacecraft control system,these uncertainties are usually addressed by robust methods.SMC has widely been utilized for robust control of speed loop by utilizing high frequencies to converge the system trajectories onto a sliding surface and remain toward the equilibrium point which causes chattering.Chattering problem causes limitation for some existing robust methods,such as sliding mode control laws.To remove these drawbacks,we combine an improved dynamic sliding mode controller and model predictive controller for spacecrafts to solve the chattering phenomenon in traditional sliding mode control.The proposed controller is capable of improving the performance of the SMC for spacecraft by avoiding chattering, reducing overshoot and increasing the response speed.Dynamic sliding model control (DSMC) makes extra dynamics into a sliding surface and helps to remove many difficulties in implementation,such as reducing chattering of control loops.The main contributions of this paper include the following subjects:

• Thispaperdealswithparameteruncertainties,unmatched model uncertainties and external disturbances.

• It aims to achieve the advantages of the dynamic sliding surface.This paper proposes a new sliding surface for satellite controller by calculating the first derivative of the input and removes chattering fundamentally.

The rest of the paper is organized as follows.Section2 considers the spacecraft attitude control problem.The design process of the dynamic sliding mode is given in Sect.3.In Sect.4, the effectiveness of the proposed dynamic sliding mode control method is verified by simulation and Sect.5 includes the conclusion.

2 Spacecraft attitude control problem

The spacecraft model is assumed to be uncertain,with variation and uncertainty of spacecraft.The MPC is used by constraining the control torque and controlling gimbaling servo angular velocity.MPC implementation guarantees feasibility and stability for the nominal system, but reaction wheels (RW) generate control torque and the control input using only an approximated model of the spacecraft and it fails to control the spacecraft in the presence of uncertainties and disturbances.To handle the existing problems,a dynamic sliding mode control scheme is combined with MPC to guarantee the convergence of the state variables of the closed-loop system.It is necessary to provide strong theoretical analysis to guarantee the feasibility and stability of the proposed method.We prove that the proposed dynamic sliding mode controller stabilizes the satellite position in the presence of uncertainties and external dynamic disturbances,while MPC implementation is used to generate feedforward trajectories and control input for angular velocity.In this section, the spacecraft attitude control problem considered in [17] and[18] and the main modeling dynamics are summarized.In this paper, a satellite is formally regarded as a rigid body which includes the solar panels and antennas(Fig.1).

whereJ∈R3×3is the inertial matrix at pointGof the bodyB,Fextandτextidentify the forces and torque acting onG,respectively.aGandΩare the inertial acceleration vector and absolute angular velocity vector of the bodyB.We assume that the external torque includes the control,gravity gradient and disturbance.Then,the dynamics of a rigid spacecraft is modeled by the following equation:

In Eq.(3),τggis(k0×Jk0)andΩ⊗is given as

3 The double-loop control structure

We apply double-loop control system which consists of an angle loop (Euler angle loop) and angular rate loop.The block diagram representation of the double-loop control system is shown in Fig.2.The MPC and the DSMC are applied for the angle and angular rate loops,respectively.The MPC algorithm is used in the outer layer as shown in Fig.2.We applied DSMC for an inner layer structure of spacecraft attitude tracking problem.The desired angular velocities(Ωd)are calculated by the MPC algorithm and given to the DSMC layer.A robust control torque (τctrl) should be found such that in the presence of disturbances/uncertainties,the angular velocities of the spacecraftΩconverge to the desired valuesΩdin finite time.

3.1 Angle loop

We applied the MPC algorithm proposed in[19]for the position loop.By spacecraft equations at sampling timeTs,a time invariant model can be achieved by the following equation:

whereA=B=C=I3×3,v(t) =Ts R(θ)ωd(t) implies the control input andy(t) is measured altitude angles.It is clear that the pairs(A,B) and(C,A) are controllable and observable,respectively.MPC looks for the minimum value

Fig.2 The proposed control structure

of a constrained optimal control problem as follows:

Changes of the inputδˆvt+k|kand ˆyt+k|kimply a future value at timet+kof the input changes(δv)and output prediction(y(t))that is assumed at timet.HpandHvare the prediction andthecontrolhorizon,respectively.itisnotedthatHv≤Hpand it is also assumed that ˆvk+i|k=vHvfor allHv≤i.The constraints are defined as

We can rewrite the cos function Eq.(7)as follows:

where

To solve the MPC problem,an estimate of the future system states must be obtained according to the current state(θ(t)),the current and future inputs.The system state prediction can be written based on the last input and the initial state as follows:

We can rewrite Eq.(11)as follows:

The prediction of the output is easily obtained from Eq.(13).

By recalling Eq.(12),the cost function can be rewritten as

where

We also rewrite cost function Eq.(14)constraints Eq.(8)in the following format:

whereEandFare easily obtained from Eqs.(14)–(16).We apply the MATLAB-based solvers (quadprog) to solve the quadratic programming problem with linear constraints.

Theorem 1The closed-loop system under the designed control law in Eq.(16)is asymptotically stable in the feasible space.

3.2 Angular rate loop

Classic sliding mode control includes two main steps.In the first step,a set of switching surfaces that represents some sort of a desired motion is represented and a continuous control law is designed in the second step to ensure convergence to the switching surfaces.We assume that the desired trajectory(Ω)is the output of the angle loop and the problem is finding the control command to force the angular rates of the spacecraft to track the desired values(Ωd),for which we need to rewrite mathematical model Eq.(3)as follows:

where

Hence,let ˜fand ˜gbe the estimate off(Ω)andg(Ω)with the known upper estimation error bound.

whereδ fis constant andδg≤1.LetΩe=Ωd-ΩandS(Ω;t)=(d/dt+λ)Ωebe the tracking error in the angular rateΩand a time varying surface with strictly positiveλ,respectively.The traditional sliding mode problem of finding robust control input can be obtained by choosing the control law outside of the sliding surface to guarantee that the system trajectories remain on the surface.

whereηis strictly positive.For obtaining the approximation of the control law(ˆu),the dynamics ˙S= 0 is solved.Then to satisfy the sliding condition(16),a term discontinuous is added to ˆu.

Itisusualtochooseklargeenoughthatguarantees(16)which causes the chattering problem.The fact is that because of the system’s inertia, the system’s state does not remain on the switching surface and starts to fluctuate near the switching surface.The small switching gain results in slowing the convergence; on the other hand, large gain yields a large chattering.A DSMC with integral switching gain will help to obtain fast convergence and low chattering.We have to define a sliding surface as follows:

whereΩe(t)=Ωd(t)-Ω(t),CandDrepresent the angular velocity error, the non-singular three-dimensional diagonal matrix and a constant scalar,respectively.

Theorem 2For the system dynamics(2)with sliding surface defined in(22),the following control law stabilizes the satellite attitude in the presence of uncertainties and external dynamic disturbances.

ProofBy taking derivation from(22),we have

We replace ˙SΩ= 0 in (24), thenC˙Ωe-D˙u1= 0.The derivative of theΩeis

According to(24)and(25),we have

Noticing the function(17),we have

It is easy to show thatV(Ω,θ)≥0 for all(Ω,θ),V(Ω,θ)=0 if and only ifΩ=θ=0 and all sublevel sets ofV(Ω,θ)are bouded.We concluded that ˙Vmpc< 0 for allθand we have to show that ˙V(Ω)≤0 for allΩ.We try to find the total derivative of the Lyapunov function candidates(˙Vdsmc).Now,taking(24)in the derivative of Lyapunov function candidates and it is noted that

From (25) and (29), one calculates ˙Vdsmc=ST(C( ˙Ωd-˙Ω)-D˙u).Consequently,the above equation gives

Transporting the above equation yields

Obviously,the derivative of the Lyapunov function is negative everywhere,then the trajectory tends to the origin,i.e.,the system is stable.

Fig.3 Trajectories of η=[φ,θ,ψ],ω and ωe for Case 1

4 Numerical examples

Numerical examples are prepared to show the advantages of the proposed design scheme.We consider the satellite model which is considered in[17].Three rotating wheels are aligned with the principal axes of the spacecraft’s body-fixed frame withJω= diag(10,6,4)×10-3.We also assume that all initial angular velocities and angles are zero and the inertia in different axes are as follows:

Then, we consider that the variation and uncertainty of spacecraft inertia matrix are 30% (δg= 1.3 andδ f=0.5).The parameterτdwhich denotes the disturbance is±[-0.4,0.4,-0.4].Other parameters of simulation are selected as follows:

Fig.4 Illustration of v(t),u(t)and Ωe(t)for Case 1

Fig.5 Trajectories of η=[φ,θ,ψ],ω and ωe for Case 2

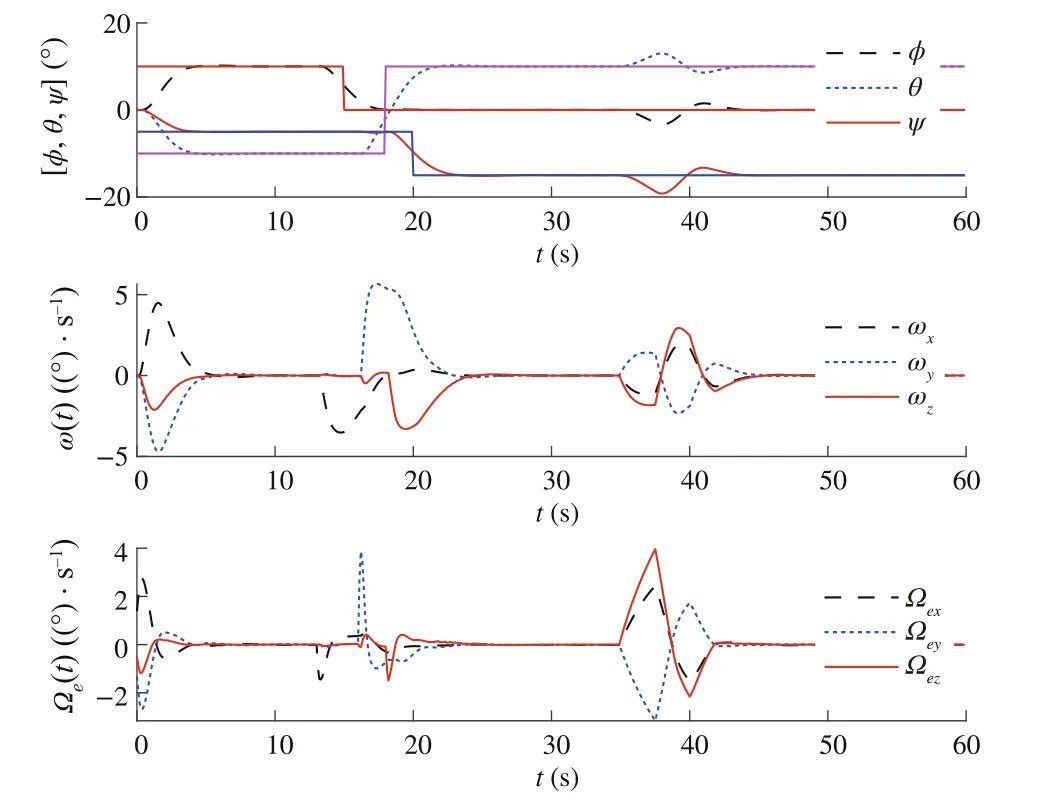
Fig.7 Trajectories of η=[φ,θ,ψ],ω and ωe for Case 3

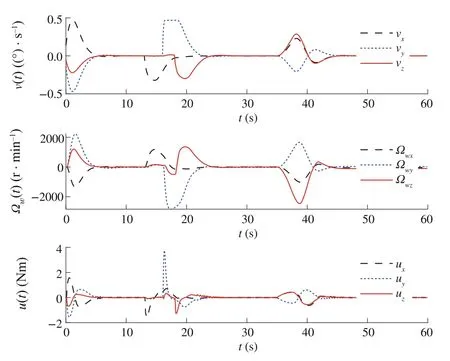
Fig.8 Illustration of v(t),u(t)and Ωe(t)for Case 3

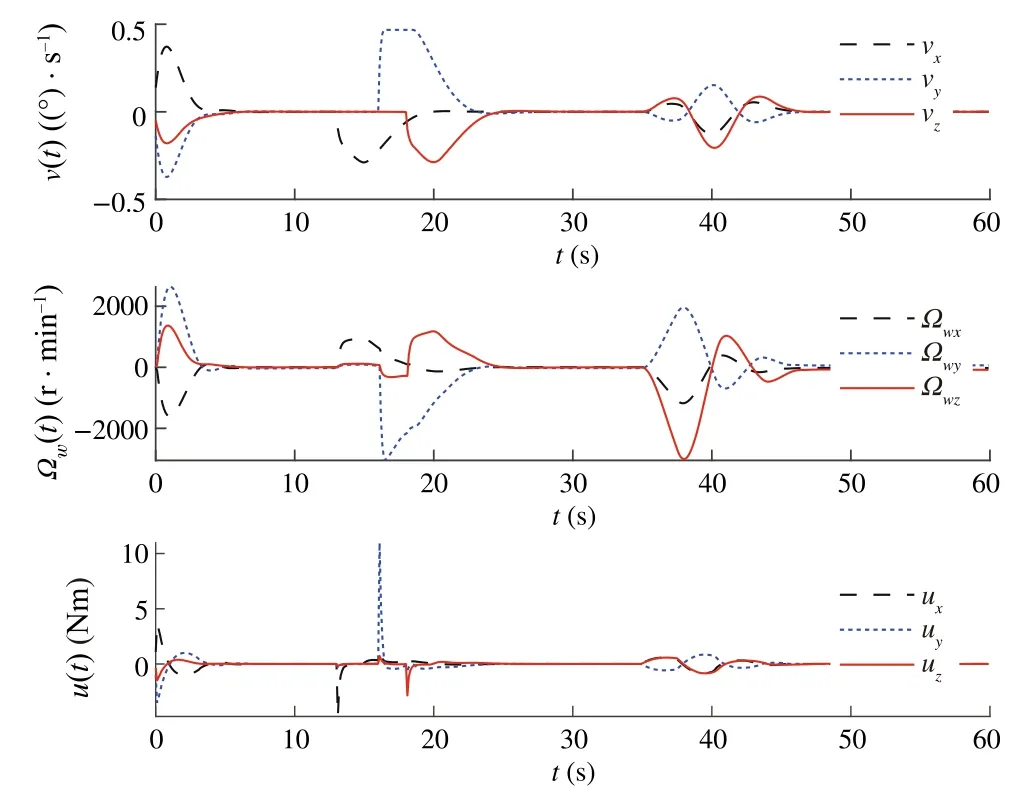
Fig.6 Illustration of v(t),u(t)and Ωe(t)for Case 2

Our goal is to illustrate the effectiveness of the DSMC method for satellite position, while MPC is used by constraining the control torque and controlling gimbal servo angular velocity.To illustrate the advantages of the proposed method from different vision, three sliding modebased model predictive approaches were performed.Three approaches include MPC with conventional sliding control(Case 1),model predictive terminal sliding control[17](Case 2) and our proposed method (Case 3).After spacecraft inertia matrix changes 30%, the controllers are put into operation; the time–response curves of three cases are depicted in Figs.3, 4, 5, 6, 7 and 8.The simulation results show that the proposed controller is robust against the simulated uncertainties.However,control torque passes over the maximum control torque produced by the RWs.Therefore,the performance of the closed-loop system in the presence of actuator saturation is considered.We determine the saturations for angular velocities of wheels and producible torque.

From the comparison,one can find that,under the presented DSMC,the states converge faster than with the SMC method.However,it is worth noting that the model predictive terminalsliding mode which is proposed by Bayat[17]is also robust against the unknown disturbances and can obtain the objectives.To have a detailed comparison between the proposed method and model predictive terminal sliding control,maximum overshootMpand settling time are compared(Tables 1 and 2).These two methods have almost the same settling time; however, the time response of the proposed method yields a small percentage overshoot compared with the model predictive terminal sliding control.On the other hand, the most important advantages of the proposed method rather than applying terminal sliding control approach for speed loop is smallerMp.

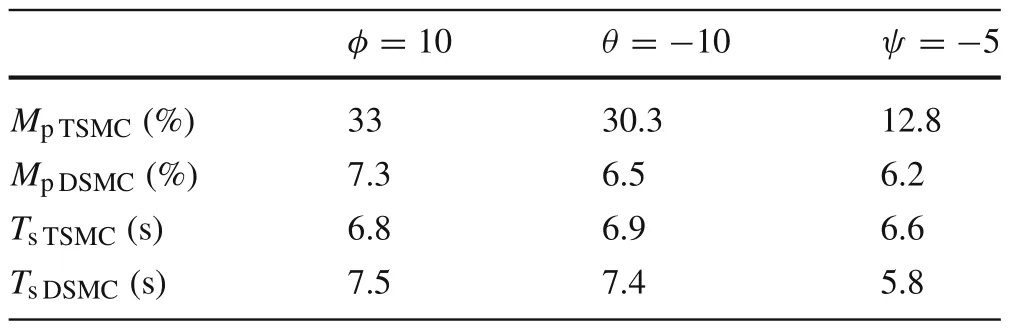
Table 1 Comparison of maximum overshoot Mp and settling time Ts(with saturation)

Table 2 Comparison of maximum overshoot Mp and settling time Ts(without saturation)

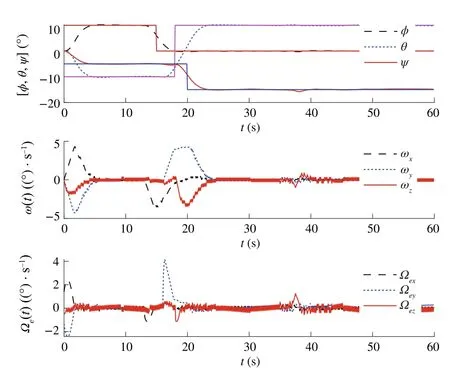
Fig.9 Trajectoriesofη=[φ,θ,ψ],ω andωe forCase1withsaturation

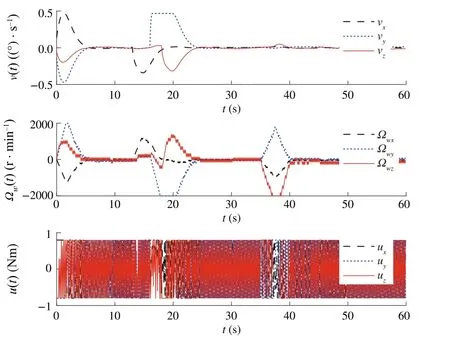
Fig.10 Illustration of v(t),u(t)and Ωe(t)for Case 1 with saturation

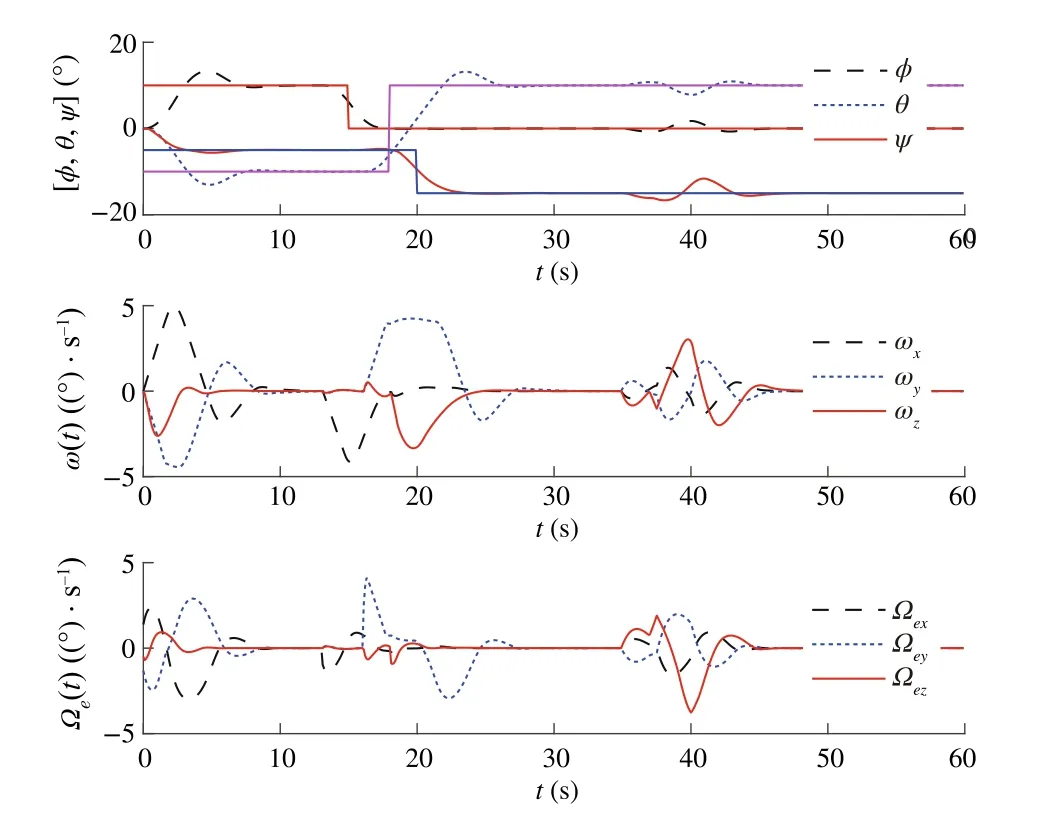
Fig.11 Trajectories of η = [φ,θ,ψ],ω and ωe for Case 2 with saturation

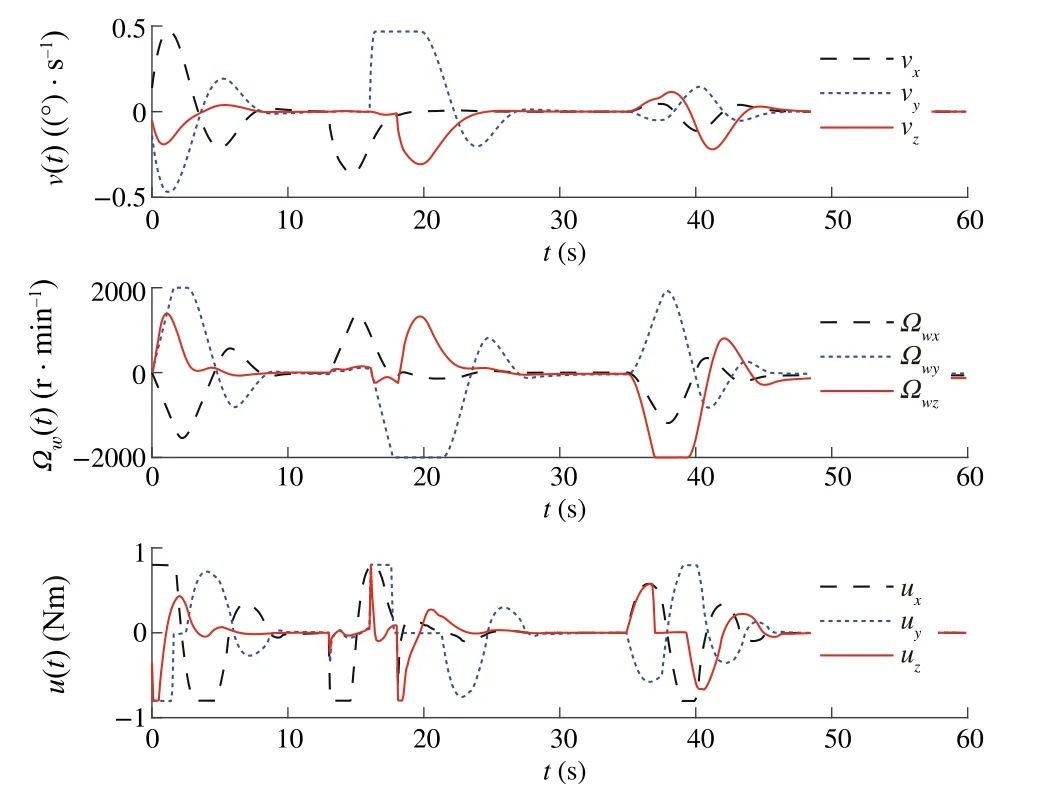
Fig.12 Illustration of v(t),u(t)and Ωe(t)for Case 2 with saturation

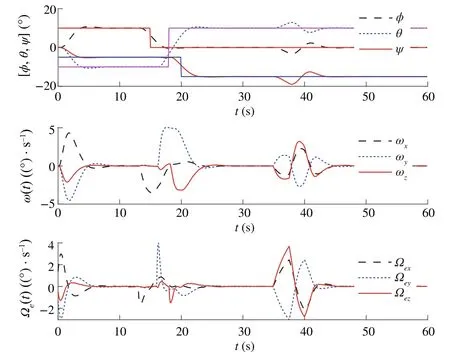
Fig.13 Trajectories of η = [φ,θ,ψ],ω and ωe for Case 3 with saturation

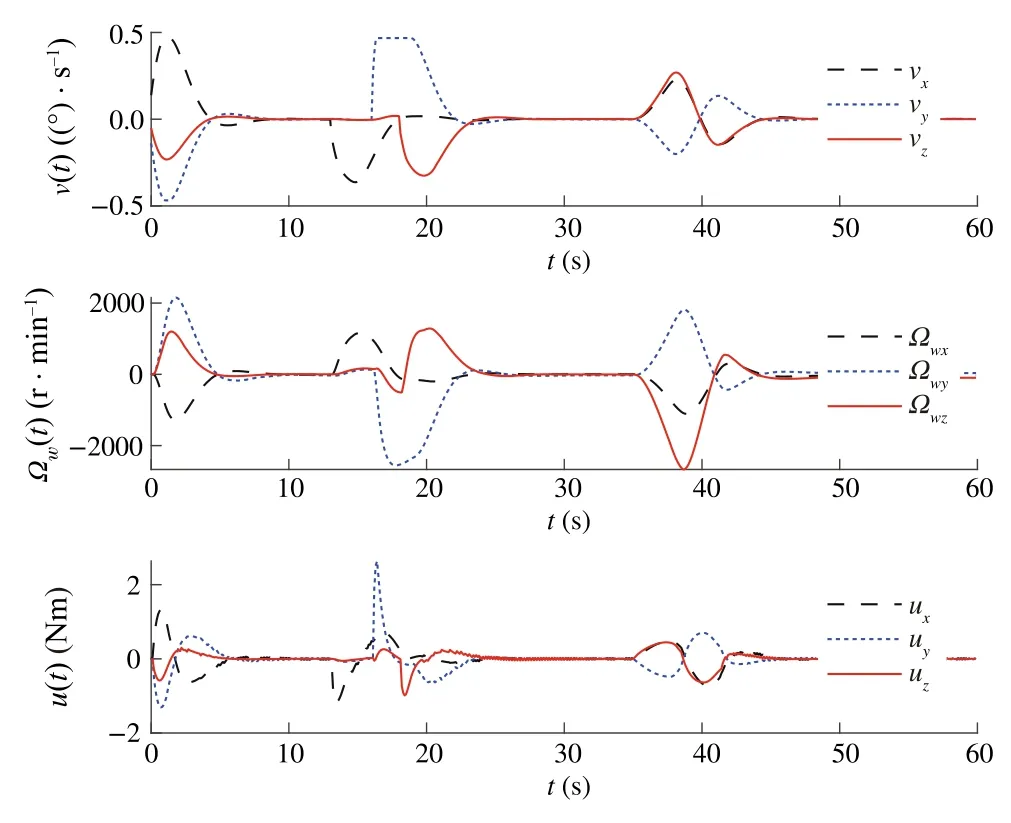
Fig.14 Illustration of v(t),u(t)and Ωe(t)for Case 3 with saturation

5 Conclusion

This study proposed a dynamic sliding mode controller for spacecrafts.The proposed controller guaranteed the stability and robust three-axis attitude tracking goal in the presence of uncertainties and disturbances given that true target points are achieved.This control strategy includes the benefits of dynamic sliding mode and integral gain.It is also shown that our algorithm is asymptotic stable.At the end of this paper, simulation results show that the DSMC control strategy have control peak decreasing, chattering removal,fast convergence, and efficient robustness to disturbances,and parametric and nonparametric uncertainty.It has to be mentioned that integration of model predictive control into dynamic sliding mode control to produce a robust nonaggressive controller should not limit the controller’s speed.The challenging factor of the proposed controller is the relatively online computational effort associated with the model predictive control, which limits its applicability.It can be concluded that what remains in designing the proposed controller for speed control is to analyze online which factors could increase the area of use for this kind of controllers.