Adaptive feedback control for nonlinear triangular systems subject to uncertain asymmetric dead-zone input

Minghui Feng·Yanjie Chang·Zhiyu Duan·Xianfu Zhang

Abstract In this paper, an adaptive control strategy is proposed to investigate the issue of uncertain dead-zone input for nonlinear triangular systems with unknown nonlinearities.The considered system has no precise priori knowledge about the dead-zone feature and growth rate of nonlinearity.Firstly,a dynamic gain is introduced to deal with the unknown growth rate,and the dead-zone characteristic is processed by the adaptive estimation approach without constructing the dead-zone inverse.Then,by virtue of hyperbolic functions and sign functions,a new adaptive state feedback controller is proposed to guarantee the global boundedness of all signals in the closed-loop system.Moreover,the uncertain dead-zone input problem for nonlinear upper-triangular systems is solved by the similar control strategy.Finally, two simulation examples are given to verify the effectiveness of the control scheme.

Keywords Dead-zone input·Dynamic gain·Adaptive estimation·Global boundedness

1 Introduction

Theresearchfieldofnonlineartriangularsystemhasobtained accumulating attention in the past several years.Quite a few mathematicalmodelsandengineeringproblemsinrealitycan be converted to the issues of global stabilization or boundedness of nonlinear triangular systems,see[1–7].Recursive design comprising forwarding and backstepping design technique is a powerful technique for studying the nonlinear triangular systems[1,2].Based on backstepping design and Razumikhin lemma, [1] studied the robust control problem for a class of nonlinear time-delay systems with triangular structure where the state feedback controllers were designed such that the global regulation was achieved.Besides, two novel control schemes were developed to solve the timedelay problem for upper-triangular nonlinear system through recursive design approach in [2].In recent years, dynamic gain becomes a creative control approach for the research of nonlinear triangular systems and plays an important role in coping with nonlinearities,which facilitates the design of the control strategy.Using dynamic gain technique,the constructivecontrolstrategieswereproposedfortime-delaynonlinear triangular systems in [3–5], and globally asymptotical stability was achieved with the help of Lyapunov–Krasovskii functionals.

When system parameters or the bounds of system parameters are unknown, the adaptive control has been widely studied.Recently, a growing number of adaptive control problems appear in practical industrial systems, see [8, 9].On the basis of this framework of backstepping design,fuzzy logic systems and neural network technique were applied to approximate the uncertain nonlinear terms, which made it convenient to compensate the complex nonlinear terms,see[10,11].Using the adaptive backstepping technique,a novel adaptive control algorithm for uncertain nonlinear systems was developed in[12]to offset the effect of uncertain input parametersbyintroducingahyperbolictangentfunction.Different with the above literature, under the circumstance of unknown growth rate,two dynamic gains were introduced to deal with the uncertain system parameter,see[13].In[14],the problem of time-delay nonlinear systems with unknown parameters was investigated using dynamic gain approach,and an adaptive state feedback control scheme was proposed.It can be seen from the above results that the backstepping design and neural network technique are commonly applied to cope with the uncertain system parameters.

In addition, uncertain dead zone input is an universal issue and occurs in many practical applications.The existence of uncertain dead-zone affects the system performance seriously.Therefore,for the sake of compensating for negative effects brought by dead-zone input,a series of relevant studies have been executed by constructing the inverse of dead-zone, see [15, 16].With further study on dead-zone input, [17] decomposed the dead nonlinearity into a linear part and a disturbance-like term.Based on this idea, some excellent results were obtained,see[18,19].Ibrir et al.[18]solved the adaptive tracking problem for nonlinear linearizable uncertain systems without constructing the dead-zone inverse.By constructing a smooth adaptive controller, the tracking control problem for a class of nonlinear system subject to time delay and dead-zone input was investigated in [19].For a class of nonlinear systems subject to fuzzy dead zone, the adaptive fuzzy controller was constructed,which guaranteed that all the signals of closed-loop system were semi-globally uniformly bounded,see[20,21].Without preciseinformationaboutthedeadzoneinput,anoutputfeedback controller was developed in [22] to ensure the global boundedness of all states, so that the problem of tracking was solved for systems in lower-triangular form.However,cognate researches on state feedback control problem for nonlinear triangular systems with uncertain dead-zone input based on dynamic gain approach have received little attention.

This paper explores the state feedback stabilisation problem for nonlinear triangular systems subject to dead-zone input.Influenced by[4,23],the dynamic gain is developed to cope with the nonlinear terms for lower-triangular system.Then, it is extended to nonlinear upper-triangular system,where a new form of dynamic gain is presented.The adaptive feedback controllers for both nonlinear lower-triangular systems and nonlinear upper-triangular systems are proposed to guarantee the boundedness of all signals in the closedloop system.The main contributions of this paper is listed as below.

(i) Unlike existing works using adaptive fuzzy backstepping design control approach, the dynamic gain technique is applied to settle the state feedback problem of nonlinear triangular systems with dead-zone input,which simplifies the form of controller as well as avoids complex iterative steps.In particular, a new dynamic gain is proposed for nonlinear upper-triangular systems.

(ii) Different from [20, 21], the global boundedness of all states of the closed-loop system is obtained.Furthermore, the convergence region around zero of all states in the closed-loop system can be small enough by adjusting relative design parameters.

(iii) Most of the existing literature about dead-zone input are aimed at nonlinear lower-triangular systems, and it has shown the feasibility of handling the effects of dead-zone and inherent nonlinearities through adaptive control strategy,see[24].Specially,it is a remarkable fact that the adaptive controller in this paper is also effective for nonlinear upper-triangular systems.

The rest of this paper is indicated as below.Section1 devotes to the problem formulation and preliminary work.Next,the main results of this work are presented in Sect.3,which includes the design of adaptive control schemes and the boundedness analysis of dynamic gain and all states for lower-triangular system as well as upper-triangular system.Then,Sect.4 provides two simulation examples to manifest the effectiveness of the adaptive control strategy.Finally,Sect.5 presents the conclusions.

Notations R, R+and Rnrepresent the set of real numbers,the set of nonnegative real numbers andn-dimensional Euclidean space,respectively.Irepresents an identity matrix with suitable dimension.The sign function sign(a)denotes that whena> 0,sign(a)= 1;whena< 0,sign(a)= -1;whena= 0, sign(a)= 0.‖·‖denotes the Euclidean norm of a vector or matrix.λmax(·) andλmin(·) stand for the maximum eigenvalue and minimum eigenvalue of a matrix,respectively.

2 Preliminaries and problem formulation

Consider the following uncertain nonlinear system

wherex(t) = [x1(t),...,xn(t)]T∈Rnandu(t) ∈R are the system state and input,respectively.The nonlinearityfi(·):R+×Rn→R is a continuous function.Assume that all states in system(1)are measurable and can be utilized in the design of control strategy.The form of uncertain actuator dead zoneN(u(t))is as follows:

where the unknown parametersmr> 0 andml> 0 represent the right and left slope of the dead-zone characteristic,respectively,br> 0 andbl> 0 denote the break points of dead-zone input.

To simplify the controller design,one can redescribe the dead-zone model(2)as follows:

where

The control objective of this paper is to develop an adaptive controller to ensure all signals of close-loop systems are globally bounded.To achieve the control objective, several necessary assumptions and lemmas are required.

Assumption 1 [19]The parametersmr>0,ml>0,br>0 andbl>0 are unknown but bounded.

Remark 1Assumption1isanecessaryconditionusedtoindicate the parameters of dead input,see[18,19,22].Obviously,one can get thatη(u)andψ(u)are bounded form(4),(5)and Assumption 1.Therefore,there exist two unknown constantsθ1andθ2satisfying thatand

Assumption 2 For eachi= 1,...,n, there exists an unknown positive constantγsuch that

Assumption 3 For eachi=1,...,n,the system nonlinearitiesfi(·)satisfy the following conditions:

whereγis an unknown constant,andfn-1=fn=0.

Remark 2In general,system(1)is known as lower-triangular system when Assumption 2 holds.On the contrary, system(1) is called upper-triangular system when Assumption 3 holds.Under Assumptions 2 or 3,system(1)includes a great quantity of nonlinear physical systems,such as mechanical interaction system of robots and nonlinear liquid level control resonant circuit system,see[6,7].Besides,many renowned studies have investigated the stability problem for a class of nonlinear systems without dead-zone input under conditions of Assumptions 2 and 3,see[4,13].

Lemma 1 [25]Let A∈Rn×n,C∈Rn×1,F∈R1×n,D1∈Rn×n and D2∈Rn×n be matrices defined as

D1= diag{1,...,n}and D2= diag{n,...,1}.Then there exist two positive constants d1,d2,one positive definite matrice P>0,and a vector Ka=[a1,a2,...,an]with ai,i=1,2,...,n being Hurwitz polynomial coefficients,such that

where B=A-CKa,P∈Rn×n,and pi,n denotes the elements in row i and column n of the matrix P,i=1,...,n.

Lemma 2 [26]For any λ∈Rand ε∈R+,the following inequality holds:

3 Main results

3.1 Adaptive controller design for lower-triangular systems

In this section, a new state feedback controller for system(1) under Assumption 2 will be developed by introducing hyperbolic functions and sign functions.One can see that system (1) satisfying Assumption 2 is indeed a nonlinear lower-triangular system,see[3,7].

Theorem 1Under Assumptions1,2,the global boundedness of all states in system(1)can be guaranteed by the state feedback controller of the following form:

with dynamic gain L being updated as

where parametersˆγ1, ˆθ1, ˆθ2are the estimated values of γ1,θ1,θ2correspondingly,and adaptive updating laws are as below:

To facilitate understanding,one divides the proof into two parts.

PartI:IntroductionofcoordinatetransformationsandLyapunov functions.

The following coordinate transformations are introduced

Therefore,system(1)can be transformed into

Next,choose the Lyapunov function candidate

where

Part II:Stability analysis.

By(14)and(16),the time derivative ofV1is given by

From Assumption 2 and(13),one gets

which implies

Significantly,

then,calculate the last term of(17)by the aid of(3)and(20)

Combining(9)and(17)–(21),one can derive that

It is not difficult to derive by Lemma 2 that

Withthehelpof(9),(11),(16),(22)and(23),thederivative ofVis calculated as

From(12),one has

After simple calculation, the following inequalities also hold

Substituting(25)–(27)into(24),one can arrive at

Note that

It follows from(29)that similar inequality can be obtained

Further,one has

Using the definition ofVin(15)and(16),there holds

Remark 3Notably,according to the form of(33),increasing∊i,i=1,2,3 and decreasingσi,i=1,2,3,one will obtain smaller convergence domain.Since the design parameters can be chosen at random, the convergence domain can be rendered small enough.Besides,increasingσ1,σ2,ρwhile decreasing∊1,∊2can make dynamic gain as well as input smaller.Therefore, to balance the size of input and convergence domain and meet the practice demand,the design parameters should be chosen appropriately.

Remark 4In this section, the adaptive controller design for lower-triangular systems is designed.The main difficulty is to deal with the uncertain dead-zone input and unknown growth rate since the lack of prior information about their bounds.Different with the[19],dynamic gain and coordinate transformation approach is introduced to deal with nonlinear terms.Besides, our systems include more nonlinear terms.Compared with [22], the proposed control scheme in this paper can make the convergence region around zero of all states (x1,...,xn) in the closed-loop system can be small enough.And using the scaling change technique,the method of stability analysis in this paper is more direct.Moreover,the design approach of controller for lower triangular systems is also applicable to upper triangular systems.

3.2 Adaptive controller design for upper-triangular systems

In this section, by introducing hyperbolic functions and sign functions, a new control strategy for system (1) under Assumption 3 is proposed to ensure that all signals are bounded.It is clear that system (1) under Assumption 3 is indeed a nonlinear upper-triangular system,see[4,7].

Theorem 2Under Assumptions1and3,the global boundedness of all states in the closed-loop system(1)can be guaranteed by the state feedback controller of the following form:

with the gain L updated by

where parametersˆγ1, ˆθ1, ˆθ2are the estimated values of γ1,θ1,θ2correspondingly,and the adaptive updating laws are as below:

Next,one divides the proof into two parts.

PartI:IntroductionofcoordinatetransformationsandLyapunov functions.

Let

Thus,system(1)can be converted into

where

wherePis given in Lemma 1.

Part II:Stability analysis.

Using Lemma 1,a simple derivation is given

Then, by Assumption 3 and coordination transformation(38),one gives the estimation of the nonlinearity terms 2zTP Fin(42)

whereγ1is an unknown constant.

From (34), (43), and Lemma 2, the following inequality holds:

Recalling(29)and(30),it is derived that

Remark 5Aimedatuncertainnonlinearupper-triangularsystems with unknown actuator input, the developed control scheme is also valid.The desired control performance can be obtained by adjusting relative design parameters similar with Remark 3.It is worth noting that the accurate information of growth rate and the characteristic about the actuator nonlinearities of nonlinear system are unnecessary,and their bounds are not required to be known.The adaptive controller in this paper can compensate for the effects of uncertain actuator nonlinearities.

Remark 6On the one hand,for ∀t∈[0,+∞),the dynamic gainL(t)is designed to satisfyL(t)≥1.It should be pointed out that the introduction of dynamic gainLis effective to estimate the unknown nonlinear terms.Note that the real but unknown parameterγ1cannot be used in the design of dynamic gain,which means the effects of the unknown nonlinear terms cannot be eliminated directly.Therefore, ˆγ1is introduced into dynamic gainL.It can be seen from the above calculation process, by designing ˆγ1delicately and incorporating the properties of such a special structure ofL,one can cope with the unknown nonlinearities efficiently.On the other hand,instead of the renowned backstepping design approach,the dynamic gain design approach is used in this paper,which avoids the problem of explosion of complexity.

4 Two simulation examples

In this section, two examples are given to verify the effectiveness of the control strategies proposed in this paper.

Example 1Consider the following system

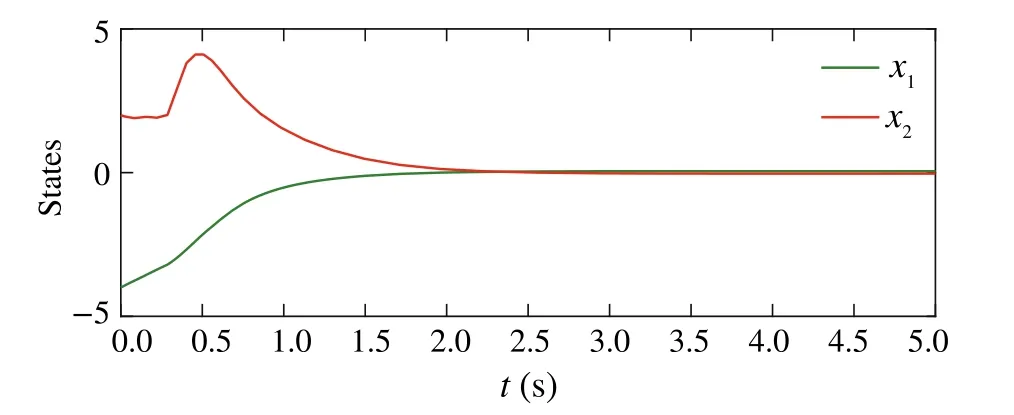
Fig.1 Trajectories of x1 and x2 in systems(47)–(51)

whereN(u)denotes the dead-zone input

It is easy to see the nonlinearities satisfy Assumption 2 withγbeing an unknown constant.To dispose of the difficulty brought by the uncertain dead-zone input and uncertain nonlinearities in system (47), one can construct the following state feedback control scheme according to Theorem 1:

whereLis the state of system

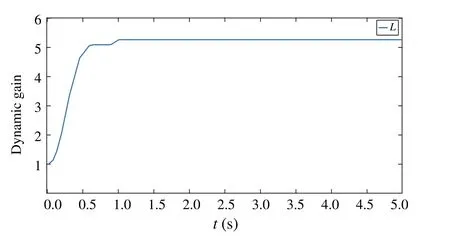
Fig.2 Trajectory of L in systems(47)–(51)

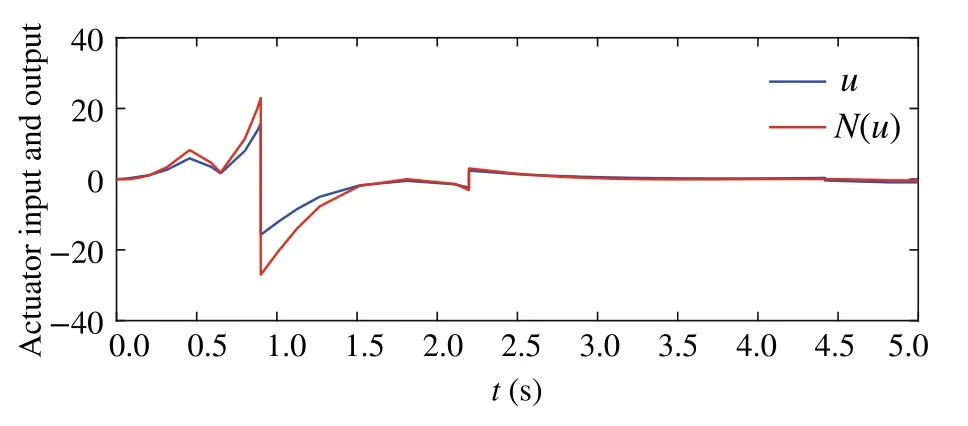
Fig.3 Trajectories of u and N(u)in systems(47)–(51)

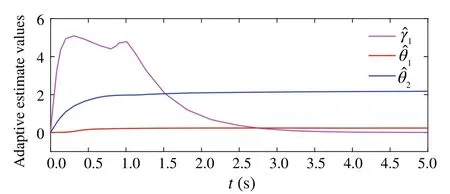
Fig.4 Trajectories of ˆγ1, ˆθ1, ˆθ2 in systems(47)–(51)

One can obtain that the control scheme can guarantee the boundedness of all states of the closed-loop system.Particularly,one can make the region of convergence of states small enough by adjusting the values of parametersρ,∊1,σ1,∊2,σ2,∊3,σ3andε.Besides, it is clear that dynamic gain and controller are bounded by Figs.2 and 3.Example 2Consider the following system

whereN(u)has the following form

It is easy to see the nonlinearities satisfy Assumption 3 withγbeing an unknown constant.One can employ the following state feedback controller from Theorem 2 to deal with the uncertain dead-zone characteristics as well as nonlinearities

Fig.5 Trajectories of x1 and x2 in systems(52)–(56)

Fig.6 Trajectory of L in systems(52)–(56)

of system(52)and achieve the control goal.

withLbeing the state of system

and updated laws of ˆγ1, ˆθ1and ˆθ2are as follows:

Similarly with Example 1, selectingKa= [1,3, 2],one gets.Then, choose the parametersρ= 0.9,∊1= 11,σ1= 0.02,∊2= 1,σ2= 0.001,∊3= 150,σ3= 0.001,ε= 2.5 and set the initial valuesx1(0),x2(0),x2(0),L(0), ˆγ1(0), ˆθ1(0), ˆθ2(0)T=[-1,1,2,1,0,0,5]T.Figures5,6,7 and 8 show the results and illustrate the validity of control strategies(54)–(56).

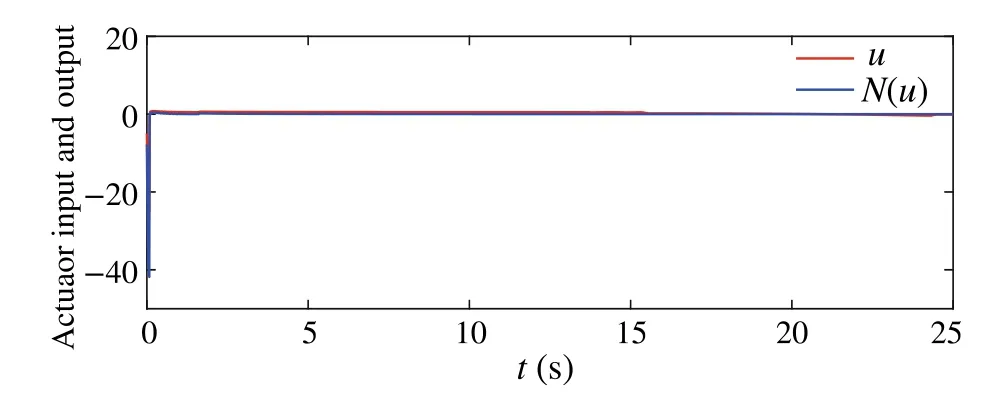
Fig.7 Trajectories of u and N(u)in systems(52)–(56)

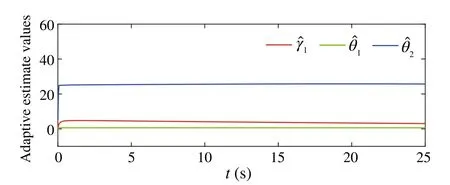
Fig.8 Trajectories of ˆγ1, ˆθ1, ˆθ2 in systems(52)–(56)

It can be observed from Fig.5 that the control scheme proposed for nonlinear upper-triangular system can also accomplish the control goal.Besides,from Figs.6 and 7,one can see that dynamic gain and the controller are bounded.

Remark 7In fact,different parameters have variable effects on the convergence region,one can make the region of convergence of all states small enough by adjusting the values of parametersρ,∊1,σ1,∊2,σ2,∊3,σ3andε.Besides,recalling control strategies we proposed,it is clear that dynamic gain and adaptive laws are also dependent on the design parameters,one can obtain appropriate dynamic gain and adaptive estimator by adjusting design parameters properly.

5 Conclusion

Inthispaper,wehaveinvestigatedtheissueofuncertaindeadzone input for nonlinear triangular system with unknown nonlinearities.Due to the lack of precise priori knowledge about the dead-zone feature and growth rate of nonlinearity for the considered system,a dynamic gain has been adopted to deal with the unknown growth rate,and the adaptive estimation approach has been employed to tackle the dead-zone characteristic without constructing the dead-zone inverse.Combined with hyperbolic functions and sign functions,two new adaptive state feedback control schemes have been proposed to ensure the global boundedness of all signals in the closed-loop system.The performance of the control scheme has been illustrated through two given simulation examples.