基于SHO-NSGA混合算法的飞机油舱管路自动布局方法

屈力刚 苏岩 邢宇飞

摘要：针对飞机油舱内部管路路径规划问题，提出一种基于改进斑鬣狗算法的飞机油舱管路自动布局方法。为了提高斑鬣狗算法的全局搜索能力以及收敛速度，在种群进化过程中引入扩散搜索机制对迭代过程中最优解进行扩散，以达到提高全局搜索能力的目的；在算法迭代后期引入深度包围机制，使其在最优解中随机搜索以提高算法的收敛速度。采用栅格法构建敷设空间数学模型，以管路路径最短为优化目标，以管路路径不与障碍物发生干涉、管路折弯角度及管路折弯半径为约束，建立管路布局优化数学模型。进一步，考虑管路的支臂布局问题，以支臂总长和支臂姿态作为支臂布局双目标优化函数，运用遗传算法NSGA-Ⅱ对管路支臂布局方案进行编码生成初始个体，设计交叉、变异规则，求解管路支臂布局的Pareto解集，进而获得管路支臂布局方案。最后，通过数值算例及管路敷设仿真验证所提方法的有效性。

关键词：管路布局；斑鬣狗算法；支臂；遗传算法；多目标优化

中图分类号：TP18

DOI：10.3969/j.issn.1004-132X.2023.15.011

Automatic Layout Method of Aircraft Tank Pipelines Based on SHO-NSGA Hybrid Algorithm

QU Ligang SU Yan XIN Yufei

School of Mechanical and Electrical Engineering，Shenyang Aerospace University，Shenyang，110136

Abstract： An automatic aircraft tank pipeline layout method was proposed based on the improved spotted hyena algorithm to address the problem of internal aircraft tank pipeline path planning. To improve the global search ability and convergence rate of the spotted hyena algorithm， the diffusion search mechanism was introduced to spread the optimal solution in the iteration processes， and then it was introduced to randomly search in the optimal solution to improve the algorithms convergence rate. The grid method was used to build the laying space mathematical model and the pipeline layout optimization mathematical model was established with the shortest pipeline path， the pipeline bending angle and the pipeline bending radius were as constraints. Furthermore， considering the pipeline arms layout problem， with arm length and arm posture as the arm layout double target optimization function， using a genetic algorithm（NSGA-Ⅱ）to code the initial individual， design cross， variation rules， to solve the Pareto solution of the pipeline arm layout sets， and to obtain the pipeline arm layout scheme. Finally， numerical examples and pipeline laying simulation were used to validate the effectiveness of the proposed method.

Key words： pipeline layout； spotted hyena algorithm； bracket； genetic algorithm； multi-objective optimization

0 引言

管路系统是飞机传递油、气、水、电等介质或动力的通道，其布局结构复杂。管路布局的优劣程度关系著产品的可靠性、可维修性。根据美国通用电器公司的总结，飞机在空中出现故障多半是由管路的破坏而导致的［1］。飞机油舱中的管路系统已经相当复杂，并且需要考虑管路在工程上的各种约束，这就使敷设的难度大大增加，因此研究飞机油舱管路的布局有重要意义。

管路系统的布局引起了广大学者的关注。樊江等［2］运用一种改进的迷宫算法并结合各种启发式规则开发了航空发动机外部管路自动敷设系统。范小宁等［3］提出一种变长编码的遗传算法，解决了船舶管路三维布局优化问题。付宜利等［4］采用混沌技术对栅格进行预处理，降低了解空间的维度，从而降低了运算的难度，提高了布局的效率，并采用改进粒子群算法对管路进行求解。张禹等［5］提出一种改进人工蜂群算法（artificial bee colony algorithm，ABC），引入锦标赛策略以解决算法过早收敛和停滞问题。赵柏萱等［6］采用快速扩展随机树和模拟退火算法完成了管路布局及优化，提出一种ASP推理机的管路系统自动评价技术，实现了管路布局的综合评价。刘佳顺等［7］采用任意时间算法和快速扩展随机树（rapidly exploring random tree，RRT）算法完成了初始化，并提出一种基于障碍物的磁吸算法，完成了线缆的贴壁处理。吴宏超等［8］提出一种基于改进A*算法的管路自动布局方法，这种方法的优点是运算速度快，但是不能保证路径为最优路径。于嘉鹏等［9］在基础天牛须算法中加入自适应变步长机制，提高了算法的搜索性能并且保留了原算法的优异性能，算法的效率大大提高了，并应用自适应天牛须算法，提出了航空发动机的管路布局优化方法。QIANG等［10］将航空发动机模型离散化，然后通过映射的方法将模型简化为多个二维平面，应用一种采用离散算子和固定长度编码机制的改进粒子群算法求解航空发动机的管路布局。YIN等［11］通过模拟人对障碍的思维，采用人工智能的手段完成了航空发动机管路的布局。REN等［12］提出了一种新的空间表示方法，简化了搜索空间，并应用改进的遗传算法求解了航空发动机的管路布局。WANG等［13］将人工解与算法解进行组合，提出一种人机合作改进的蚁群优化算法，应用这种方法不仅提高了收敛速度，而且提高了解的质量。WU等［14］提出一种结合改进启发式函数、突变机制和动态参数机制的改进蚁群优化算法，解决了半潜式生产平台油气处理系统的PRD（pipe routing design）问题。ZHOU等［15］利用Lee算法与轮盘赌相结合的方法建立了遗传算法的初始种群，并采用遗传算法对航空发动机外部管路布局进行求解，提出一种基于Lee算法和遗传算法的飞机发动机外部管路自动布局方法。关于飞机舱室上的管路布局，NEUMAIER等［16］通过一种管路与管路之间的距离处理方法与管路弯曲处理方法来处理非法的路径，采用模拟退火算法对路径进行优化。关于飞机上线束布局，ZHU等［17］采用A*算法完成了飞机线束的布局；ZHU等［18］设计了一种两步混合优化策略，实现了飞机线束的自动布局。

上述文献对船舶、航空发动机等复杂空间内管路的自动布局问题开展了广泛且深入的研究，取得了相应的成果，然而，直接运用投影法或视线法［19］难以直接适用于飞机油舱内的管路自动布局；另外，针对船舶管路的自动敷设主要解决正交管路的自动敷设问题［20］，但油舱中的管路以非正交路径为主。本文提出一种基于改进斑鬣狗算法与双目标遗传算法的飞机油舱管路路径敷设与支臂优化布局算法，针对飞机油舱的复杂敷设空间建立栅格模型，运用改进斑鬣狗算法、遗传算法对该问题进行求解，最后进行了管路敷设与支臂布局的仿真验证。

1 管路自动布局问题分析

1.1 总体思路

飞机油舱的空间较大，路径求解计算耗时相对较长，为提高算法效率并兼顾路径求解精度，本文采用等比例缩小模型的方法对模型进行处理，通过对斑鬣狗算法进行改进来设计管路自动求解算法。然后根据管路支臂的长度、支臂安装的便利性（即支臂的姿态设计）对管路支臂进行布局优化，生成管路的布局信息。这样采取分步处理策略的好处是可以提高管路自動布局求解的运算效率，更符合实际工程需求。

1.2 管路布局数字化模型表达

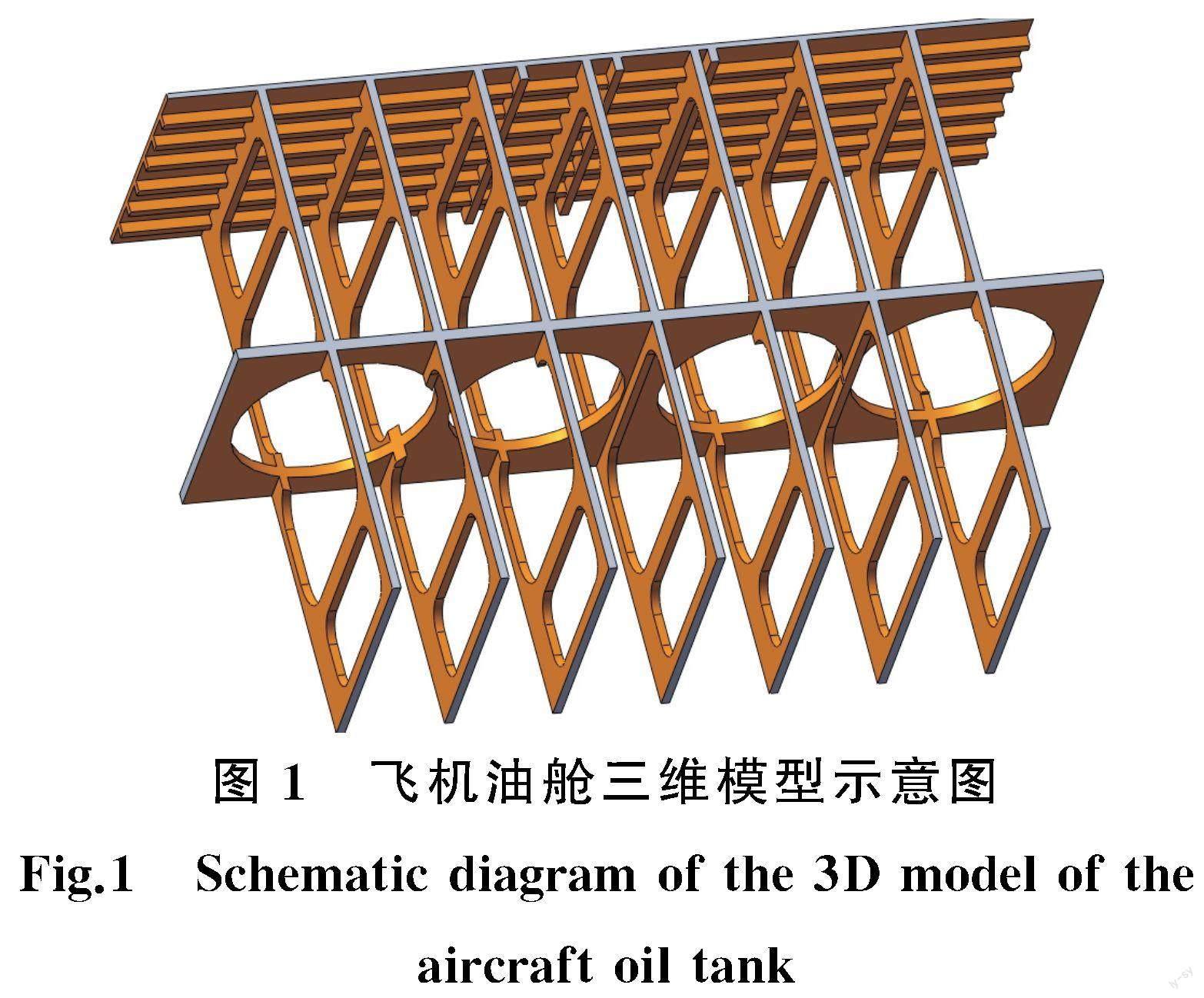
目前路径规划中通常采用栅格地图，栅格地图索引具有简单直观的优点，在管路布局中栅格地图通常是首选，所以本文采用栅格地图来建立布局模型，其三维模型如图1所示，局部栅格划分如图2所示。

1.3 飞机管路布局考虑的工程约束

（1）管路长度应最小，以减小管路质量及占用空间。

（2）管路路径不能与障碍物发生干涉。

（3）管路折弯角度不应小于90°。

（4）管路折弯半径一般为管路直径的3倍。

（5）管路折弯跨距应大于折弯半径的3倍。

（6）为避免振动，需要在管路上安装支臂。

1.4 飞机管路布局优化数学模型

根据飞机管路布局的工程规则，构建管路布局优化数学模型如下：

（1）管路路径不能与障碍物发生干涉，该目标通过惩罚函数来实现，具体方法为：采用直线插补的方法对管路路径离散化形成若干点的集合，并分别判断每个点在栅格地图上是否为障碍，并保留路径与模型干涉点的数量，计算公式为

式中，O为路径干涉惩罚值；m为路径穿过障碍的个数。

（2）管路折弯角度，该约束条件通过惩罚函数来解决，计算公式为

式中，A为路径折弯角度的惩罚值；Ai为第i个节点处的折弯角度惩罚值；dVar为种群维度即管路折弯次数（未算起点终点）；θi为路径第i个节点处的折弯角度。

（3）管路折弯跨距，该约束条件通过惩罚函数来实现，计算公式为

式中，S为折弯跨距惩罚值；Sj为第j段路径的跨距惩罚值；d为折弯跨距的最小限度，其值为管路折弯半径的3倍；dj为管路的折弯跨距。

综上，将管路节点坐标作为变量、上述工程条件作为约束条件建立管路敷设的数学模型：

minF=Lp+Oα+Aβ+Sγ（6）

式中，F为管路适应值；Lp为管路的总长度；α、β、γ为常数，其值根据管路的长度设定，以避免与管路的长度相差过大而导致计算结果不精确。

关于支臂优化目标，本文考虑采用管路支臂总长度f1和管路支臂位置姿态f2两个优化目标，具体公式如下：

式中，dp为支臂间距；HDk为第k和第k+1个支臂间距惩罚值；H为惩罚值；δ为常数，其值据实际情况而定；m为当前管路的支臂数量；Lb为支臂总长度；φl为第l个支臂相对于垂直方向的角度；φ为每个支臂相对于垂直方向向上的角度平均值。

2 改进斑鬣狗算法

斑鬣狗算法是由DHIMAN等［21］提出的一种新型的优化算法。斑鬣狗算法具有运行效率高、收敛速度快等特点，与灰狼算法、遗传算法、多元宇宙优化算法等诸多算法相比，斑鬣狗算法对较复杂的求解有较好的表现，在诸多函数计算方面表现均优于其他算法［22］。

2.1 斑鬣狗算法

斑鬣狗算法主要模拟了斑鬣狗捕杀猎物的行为，包括搜索、包围、狩猎、攻击四个过程。

2.1.1 包围

斑鬣狗具有熟悉并判断猎物的位置从而有包围它们的能力。该行为的数学模型具体描述为

Dh=|B.Ps（t）-Pb（t）|（12）

B=2r1（13）

式中，Dh为斑鬣狗个体与猎物的距离；t为迭代次数；Ps为猎物的位置；Pb为斑鬣狗个体位置；B为摇摆因子。

斑鬣狗的个体位置更新为

式中，E为收敛因子；r1、r2为［0，1］间的随机数；h为控制因子，随迭代次数的增加而减少，取值范围为［0，5］；tmax为最大迭代次数。

2.1.2 狩猎

斑鬣狗通常依赖群体之间的可信赖网络以及识别猎物的位置来捕杀猎物，该机制的数学模型描述为

Dh=|B.Ph-Pk|（17）

Pk=Ph-E.Dh（18）

Ch=Pk（1）+Pk（2）+…+Pk（N）（19）

式中，Ph为当前迭代最优解；Pk为斑鬣狗位置；N为当前迭代最优解中适应值相近的个数；Ch为N个最优解的集群。

N的计算公式如下：

N=Countn（Ph，Ph+1，…，（Ph+M））（20）

式中，M在原算法中为［0.5，1］区间内的值，在本问题中更改为当前最优解的适应值的20%。

2.1.3 攻击

斑鬣狗在最后的捕食阶段开始攻击猎物，斑鬣狗会向猎物发起攻击，其攻击方式为多个斑鬣狗攻击一个猎物。通过攻击后斑鬣狗的适应值来确定新的种群，攻击猎物的数学模型如下：

Pt=Ch/N（21）

式中，Pt为发起攻击后斑鬣狗的位置。

2.1.4 搜索

斑鬣狗根据位于最优解集群Ch中的斑鬣狗集群的位置来搜寻猎物，当|E|>1时，斑鬣狗将会分散开，远离当前的猎物，并寻找更合适的猎物位置，这种搜索机制视为全局搜索。

2.2 改进斑鬣狗算法

由于原算法不足以满足管路敷设的需求，故需要引入改进策略，例如重心邻域反向学习［22］、在包围时随机引入额外个体［23］、引入黄金正弦算法和混沌策略［24］等。本文提出一种深度包围的进化机制，以提高种群的多样性，特别是在迭代末期能提高算法的收敛性能；另外提出一种基于初始化的扩散搜索机制，在进化过程中每迭代一次就运用种群初始化生成一个新的个体，并基于该个体使最优种群向外扩散，以达到全局搜索的能力且降低算法进入局部最优的概率。

2.2.1 深度包围

斑鬣狗算法有着前期大范围搜索、后期小范围搜索的特点，但是由于小范围搜索时间较短，可能导致收敛力度不够，并不能得到全局最优解，故提出一种深度包围机制，在迭代次数达到一定层次时对最优种群进行深度包围，进化机制如图3所示。具体做法如下：①生成2个随机整数Bwz1、Bwz2；②应用下式计算最优个体之间距离：

Dh=|B.Ph（Bwz1）-Ph（Bwz2）|

③应用下式计算更新后个体位置：

Pd=Ph（BBwz1）-E.Dh

式中，Pd为深度包围后个体位置；Bwz1、Bwz2为随机整数，取值范围为［1，nvar］，nvar为种群数量。

④计算种群适应值。

2.2.2 扩散搜索

斑鬣狗算法有着较好的收敛性，但是可能由于过早的收敛而陷入局部，无法得到全局最优解。为了提高算法的全局搜索性，本文提出一种扩散搜索的机制，具体原理如下：①应用初始化生成一个新的个体；②通过下式计算新个体与最优种群的距离：

Dh=|B.Ph-Pz|

式中，Pz为初始化生成一个新的个体。

③通过下式计算搜索后个体位置：

Px=Ph-E.Dh-h.Dh

④计算搜索后种群适应值。

3 基于改进斑鬣狗算法和多目标遗传算法的管路布局

3.1 改进斑鬣狗算法编码方式

改进斑鬣狗算法首先需要进行编码将待优化问题转化为算法能够搜索的参数形式。由于飞机油舱管路的布局具有连续性的特点，故将管路模型转化为若干节点，这些节点坐标组成路径矩阵P：

P=

［（x1，y1，z1） （x2，y2，z2） … （xdVar，ydVar，zdVar）］

矩阵P中存放管路节点信息，一条完整的路径还需要有起始点（x0，y0，z0）及目标点（xe，ye，ze）。

3.2 基于多目标遗传算法的支臂布局

工程中为了降低管路的振动，需要在管路上安装管路支臂，管路支臂是支撑和固定管路的重要装置，合理的布局支臂能有效减轻管路的振动。

3.2.1 编码生成初始种群

本文采用可变长度编码即将一条路径上一个支臂坐标作为一个基因片段，并将这些基因片段合并成一个染色体即一个个体，且不限制基因片段的个数，并且要求支臂坐标不会脱离管路。

初始种群由一定数量的染色体组成，因为初始种群是算法进化的起点，所以初始种群的优劣程度会对算法产生巨大影响，需要对种群初始化进行设计。具体方法如下：

（1）通过直线插补的方式对管路路径进行离散化，将路径转化为点集，如图4所示。

（2）如图4b所示，在路径线段p（p=1，2，…）上随机生成一个支臂q（q=1，2，…）。

（3）计算支臂q与节点p的距离是否满足必须安装支臂的条件，并判断该节点是否为最后一个节点。

（4）如果该节点不是最后一个节点且满足安装支臂条件，则p←p+1，否则p不变。q←q+1并转步骤（2）；如果是最后一个节点且不满足安装支臂的条件，则转步骤（5）。

（5）结束，保存支臂信息并显示最后结果，保存支臂信息。

3.2.2 交叉

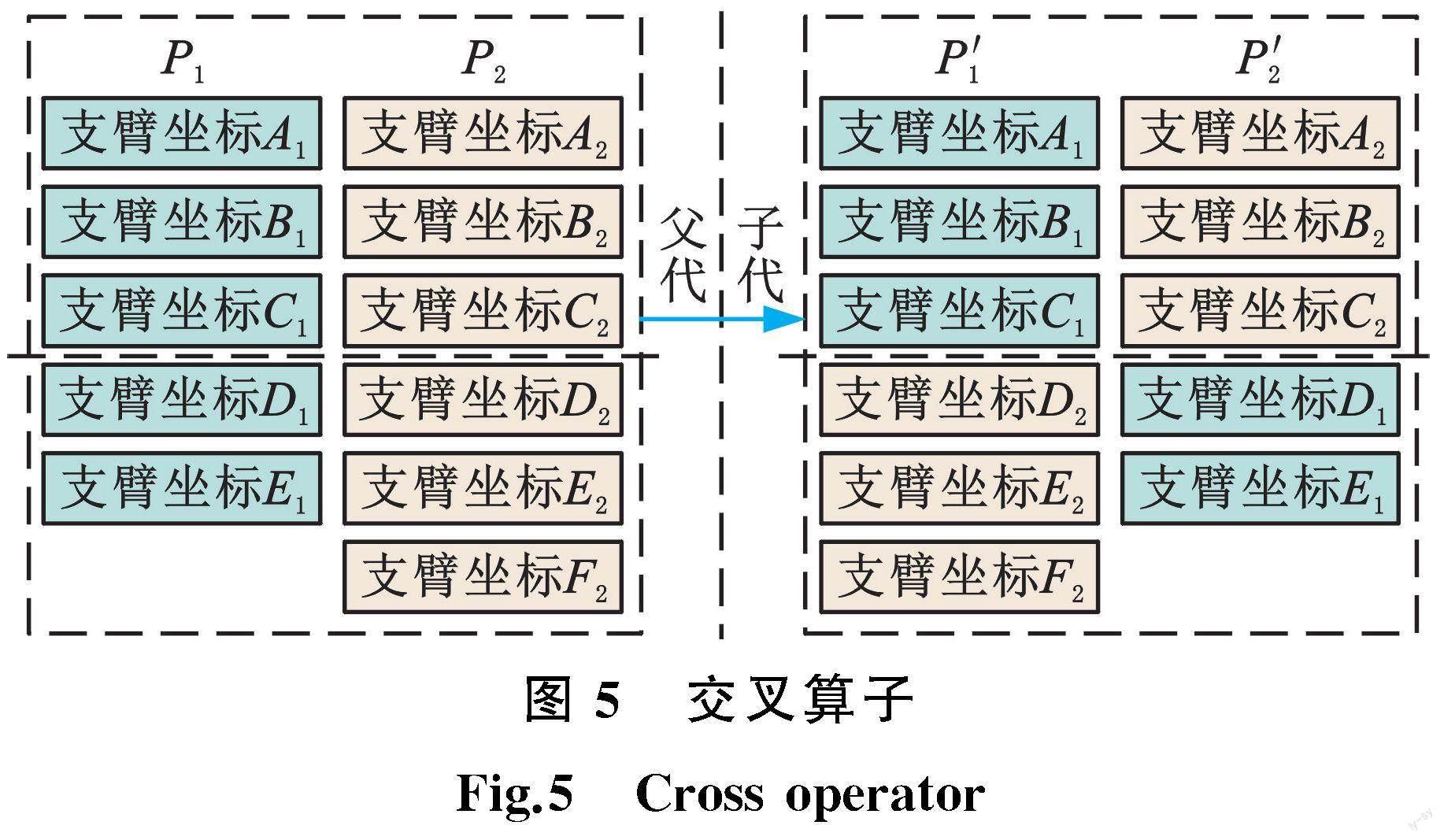
交叉算子原理如图5所示，首先在父代個体中选择支臂数量少的一个，并在父代个体P1和P2支臂数量少的个体中随机选择一个支臂作为交叉节点，以交叉节点为限将P1和P2支臂坐标交叉互换，形成子代个体P1′和P2′。

3.2.3 变异

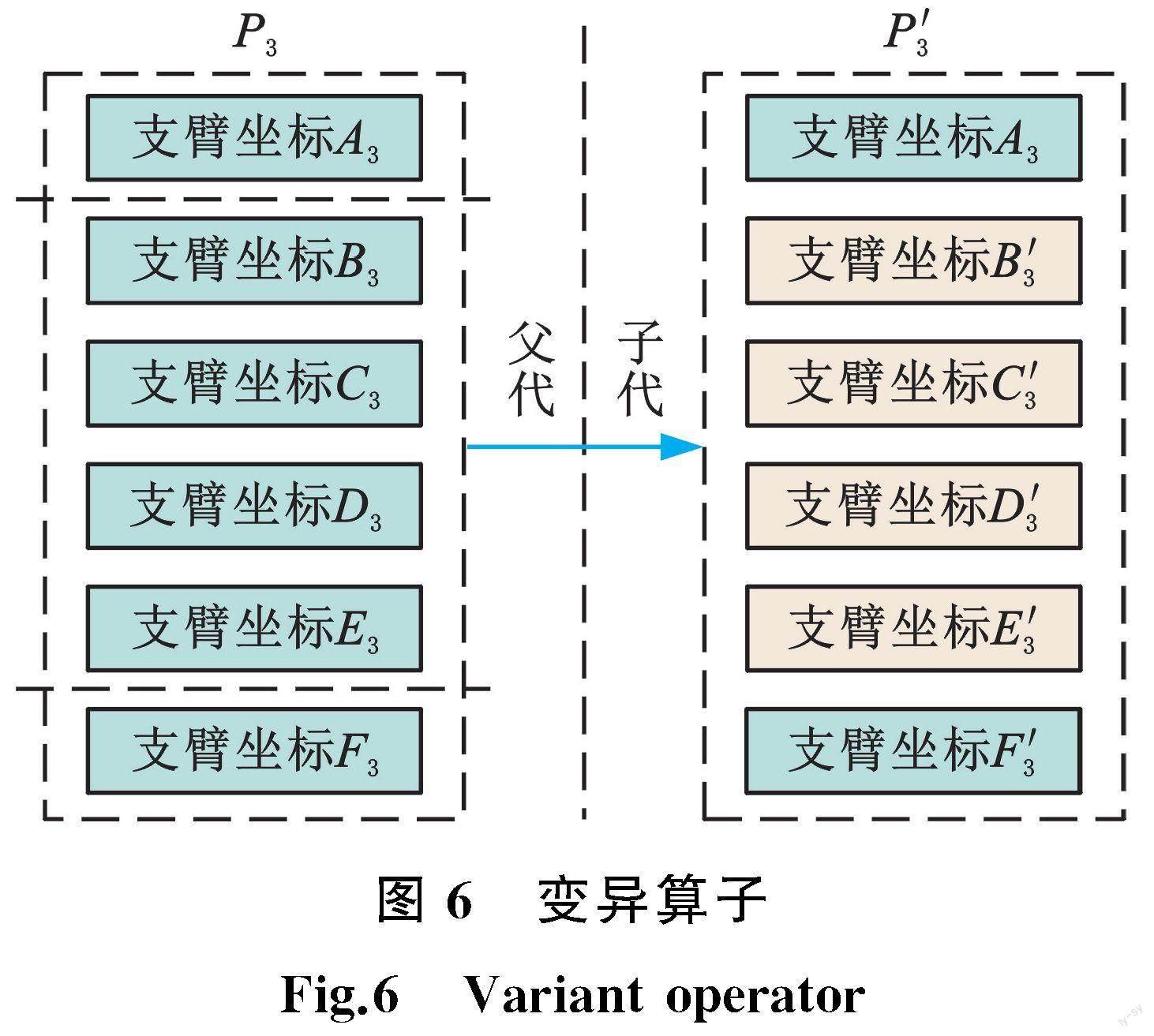
变异算子原理如图6所示，首先在父代个体P3中随机选择一个或几个支臂坐标，使其在本段管路上随机偏移并代替原来的个体，形成子代个体P3′。

3.3 算法流程图

算法流程图见图7。

4 实例验证

为了验证改进算法的可行性，对算法进行数值算例与管路敷设算例验证。测试的硬件环境如下：Intel（R）Core（TM）i5-7300HQ CPU@2.50 GHz，内存8 GB，编程环境为MATLAB 2022a。

4.1 数值算例

为验证改进斑鬣狗算法的有效性，本文分别通过以下4个典型的测试函数对改进算法的性能进行测试：

其中，f1（x）是单峰值的二次函数；f2（x）是一个单峰值函数，其最小值位于一个抛物线谷中，尽管抛物线谷容易找到，但是很难收敛到最小值；f3（x）在区间内存在多个分布均匀的极小值点，因此很难找到最优解；f4（x）是原斑鬣狗算法的测试函数之一，存在多个极小值点。

实验参数设置如下：改进斑鬣狗算法、原斑鬣狗算法的种群数量均为30，迭代次数为1000。粒子群算法种群数量为30，惯性权值为1，每次迭代减小0.01，c1=c2=2。三种算法独立运行10次的平均最优解见表1。

由表1和图8可以看出，对于这4个测试函数，在相同的迭代次数下运行，改进斑鬣狗算法的平均最优解均优于粒子群算法和斑鬣狗算法。图8a和表1的数据显示，相比原算法和粒子群算法，改进算法的收敛能力大大提高；图8b显示，改进算法前期的搜索能力大大提高；由图8c、图8d可以看出，改进算法比原算法和粒子群算法的收敛效果都好，其中f3（x）、f4（x）存在大量的局部最优解，所以改进算法跳出局部最优和克服早期收敛的能力大大提高。通过对比原算法［21］的测试函数可以发现，改进算法在计算复杂函数上有较强的搜索能力，且保留了原算法优异的性能。由于适应度函数的变化范围较大，为了便于比较，图8a、图8b、图8d中各进化曲线的横坐标采用迭代次数，纵坐标采用适应值的对数值，由于图8c观察不明显，故以适应值和迭代次数作为坐标轴。

4.2 路径规划算法对比实验

为验证改进斑鬣狗算法的高效性，与原斑鬣狗算法、粒子群算法、遗传算法［25］进行对比。实验参数设置如下：斑鬣狗算法与改进斑鬣狗算法的种群数量均为30，管路节点数量为4。粒子群算法的种群数量为30，管路节点数量为4，惯性权值为1，最小值为0.4，本文采取凹函数递减策略［26］，c1=c2=2。遗传算法参数设置如下：种群数量30，交叉率0.9，变异率0.1。T型地图见图9，其中红色为起点，坐标为（35，28，3），黑色为终点，坐标（35，20，3），图9中只给出二维图。

为了便于测试算法的性能，分别采用迭代次数50、300、500，分别独立运行3次来测试算法对管路布局方面的性能，测试结果见表2，其数据皆为路径长度。图10所示为三种算法在迭代次数为500时的最优路徑。由于改进斑鬣狗算法和PSO算法所得解x轴、y轴数值相同，z轴数值不同，所以图10a和图10c相同。由表2和图10可以发现，相比原算法，改进斑鬣狗算法的收敛能力变强了，由表2中数据可以看出，改进后算法收敛效果略优于粒子群算法和遗传算法，并且能计算出全局最优解66.8658。

4.3 管路仿真测试

为了验证本文改进算法的有效性，以飞机油舱内部管路为例，在图2中尺寸为2000 mm×1000 mm×3000 mm的飞机油舱内敷设4根管路且管路间距不小于2 mm，考虑到油舱体积过大算法计算速度过慢，将模型等比例缩小80%，实际布局空间为400 mm×200 mm×600 mm，其中管路直径为30 mm，管路的折弯半径为90 mm，管路的直线长度不小于270 mm。改进斑鬣狗算法的参数设置如下：种群大小nvar=30，种群维度（管路节点数量）dvar=4，迭代次数tmax=1000，管路半径R=15 mm，管路折弯半径r=90 mm，折弯跨距倍率3，α=β=γ=Lp。基于本文方法应用MATLAB得到4条管路的布局结果，如图11所示。

4.4 管路支臂仿真测试

本文采用图11中绿色的管路为优化支臂的管路，应用遗传算法对管路支臂进行求解，其中遗传算法参数设置如下：种群大小为50，迭代次数为100，交叉率为0.7，变异率为0.02，δ=100。

经过计算得出支臂布局如图12所示，图8a非支配解1中存在8个支臂，是支臂总长度最长的一个但也是支臂角度最平滑的一个；图8b非支配解2和图8c非支配解3中存在7个支臂，其中图8b非支配解2的支臂3和4要比图8c非支配解3的长，但角度要比非支配解3平滑；图8d非支配解4中存在6个支臂，是这4个解中长度最小的一个，但角度的平滑程度没有前3个解好。所对应支臂的Pareto解集分布如图13所示。结果表明，在飞机油舱管路的支臂布局中能够得到满足条件的支臂Pareto解集，支臂布局可以根据实际情况选取所需要的敷设方案。

5 结语

针对飞机油箱管路布局问题，本文提出了基于改进斑鬣狗算法的管路自动布局方法，引入扩散搜索和深度包围机制，提高了算法的广域搜索能力与收敛性，最终通过数值算例与T型地图证明了所提方法的有效性，并通过实例验证证明了该方法的可行性；进一步提出一种管路支臂的评价方式，以支臂长度和支臂姿态作为优化目标，应用NSGA-Ⅱ算法对管路支臂进行优化，验证了所提方法的可行性。

参考文献：

［1］ 樊江， 陈志英， 王荣桥. 航空发动机外部管路多Agent协同设计系统框架［J］. 航空动力学报， 2006， 21（1）：186-189.

FAN Jiang， CHEN Zhiying， WANG Rongqiao. Aviation Engine External Pipeline Multi-agent Collaborative Design System Frame［J］. Journal of Aviation Dynamics， 2006， 21（1）：186-189.

［2］ 樊江， 马枚， 杨晓光. 航空发动机外部管路自动敷设研究［J］. 机械设计， 2003， 20（7）：21-23.

FAN Jiang， MA Mei， YANG Xiaoguang. Research on Automatic Laying of Aero-engine［J］. Machine Design， 2003， 20（7）：21-23.

［3］ 范小宁， 林焰， 纪卓尚. 船舶管路三维布局优化的变长度编码遗传算法［J］. 中国造船， 2007， 48（1）：82-90.

FAN Xiaoning， LIN Yan， JI Zhuoshang. Variable Length Coding Genetic Algorithm for Optimized 3D Layout of Ship Pipeline［J］. Chinese Shipbuilding， 2007， 48（1）：82-90.

［4］ 付宜利， 封海波， 孙建勋， 等. 机电产品管路自动敷设的粒子群算法［J］. 机械工程学报， 2007， 43（11）：194-198.

FU Yili， FENG Haibo， SUN Jianxun， et al. Automatic Pipe-routing Particle Swarm Optimization Algorithm in Electromechanical Products［J］. Chinese Journal of Mechanical Engineering， 2007， 43（11）：194-198.

［5］ 张禹， 白晓兰， 武芄睿. 基于ABC算法的航空发动机管路自动优化布局［J］. 东北大学学报（自然科学版）， 2013， 34（10）：1461-1464.

ZHANG Yu， BAI Xiaolan， WU Wanrui. Automatical Optimization of Aero-engine Pipe-routing Layout Based on ABC Algorithm［J］. Journal of Northeastern University（Natural Science Edition）， 2013， 34（10）：1461-1464.

［6］ 赵柏萱， 刘检华， 宁汝新， 等. 一种基于工程规则的管路自动布局与综合优化技术［J］. 机械工程学报， 2015， 51（21）：121-131.

ZHAO Boxuan， LIU Jianhua， NING Ruxin， et al. An Automatic Pipe Routing and Optimization Technology Based on Engineering Constraints［J］. Journal of Mechanical Engineering， 2015， 51（21）：121-131.

［7］ 刘佳顺， 刘检华， 张之敬， 等. 基于任意时间 RRT 算 法的三维自动布线技术［J］. 机械工程学报， 2016， 52（13）：156-165.

LIU Jiashun， LIU Jianhua， ZHANG Zhijing， et al. Anytime RRT Based Cable Automatic Routing under Three-dimensional Environment［J］. Journal of Mechanical Engineering， 2016， 52（13）：156-165.

［8］ 吴宏超， 刘检华， 唐承统， 等．基于改进A*算法的管路自动布局设计与优化方法［J］. 计算机集成制造系统， 2016， 22（4）：945-954.

WU Hongchao， LIU Jianhua， TANG Chengtong， et al. Automatic Pipe Layout Design and Optimization Method Based on Improved A* Algorithm［J］. Computer Integrated Manufacturing Systems， 2016， 22（4）：945-954.

［9］ 于嘉鵬， 袁鹤翔， 杨永华， 等. 基于自适应天牛须算法的航空发动机管路布局优化［J］. 机械工程学报， 2020， 56（20）：174-184.

YU Jiapeng， YUAN Hexiang， YANG Yonghua， et al. Optimization of Aero-engine line Layout Based on Adaptive Antenna Algorithm［J］. Journal of Mechanical Engineering， 2020， 56（20）：174-184.

［10］ QIANG L， WANG C. Pipe-assembly Approach for Aero-engines by Modified Particle Swarm Optimization［J］. Assembly Automation， 2010， 30（4）：365-377.

［11］ YIN Y H， ZHOU C， ZHU J Y. A Pipe Route Design Methodology by Imitating Human Imaginal Thinking［J］. CIRP Annals—Manufacturing Technology， 2010， 59（1）：167-170.

［12］ REN T， ZHU Z L， DIMIROVSKI G M， et al. A New Pipe Routing Method for Aero-engines Based on Genetic Algorithm［J］. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering， 2014， 228（3）：424-434.

［13］ WANG Y L， YU Y Y， KAI L， et al. A Human-computer Cooperation Improved Ant Colony Optimization for Ship Pipe Route Design［J］. Ocean Engineering， 2018， 150：12-20.

［14］ WU L， TIAN X， WANG H， et al. Improved Ant Colony Optimization Algorithm and Its Application to Solve Pipe Routing Design［J］. Assembly Automation， 2019， 39（1）：45-57.

［15］ ZHOU Qian， LYUYanjie. Research Based on Lee Algorithm and Genetic Algorithm of the Automatic External Pipe Routing of the Aircraft Engine［J］. International Journal of Mechanical Engineering and Applications， 2020， 8（1）：40-44.

［16］ NEUMAIER M， KRANEMANN S， KAZMEIER B， et al. Automated Piping in an Airbus A320 Landing Gear Bay Using Graph-based Design Languages［J］. Aerospace， 2022， 9（3）：9030140.

［17］ ZHU Zaoxu， van TOOREN M J L， ROCCA G L. A KBE Application for Automatic Aircraft Wire Harness Routing［C］∥53rd AIAA/ASME/ASCE/AHS/ASC Structures， Structural Dynamics and Materials Conference. Honolulu， 2012：AIAA2012-1843.

［18］ ZHU Z， ROCCA G L， van TOOREN M J L， et al. A Methodology to Enable Automatic 3D Routing of Aircraft Electrical Wiring Interconnection System［J］. CEAS Aeronaut Journal， 2017， 8：287-302.

［19］ 柳強， 王成恩， 任涛， 等. 基于粒子群算法的航空发动机管路布局方法［J］. 东北大学学报（自然科学版）. 2009， 30（7）：940-943.

LIU Qiang， WANG Chengen， REN Tao， et al. PSO-based Pipe Routing Approach for Aircraft Engine［J］. Journal of Northeastern University（Natural Science Edition）， 2009， 30（7）：940-943.

［20］ 熊勇， 张加， 余嘉俊， 等. 船舶三维管路智能布局优化算法［J］. 计算机应用， 2020， 40（7）：2164-2170.

XIONG Yong， ZHANG Jia， YU Jiajun， et al. Intelligent Layout Optimization Algorithm for 3D Pipelines ofShips［J］. Computer Application， 2020， 40（7）：2164-2170.

［21］ DHIMAN G， KUMAR V. Spotted Hyena Optimizer：a Novel Bio-inspired Based Meta Heuristic Technique for Engineering Applications［J］. Advances in Engineering Software， 2017， 114：48-70.

［22］ 李杰. 斑鬣狗优化算法及其应用研究［D］. 南宁：广西民族大学， 2019.

LI Jie. The Optimization Algorithm of Spot Hyena and Its Application［D］. Nanning：Guangxi University for Nationalities， 2019.

［23］ SABAHNO M， SAFARA F. ISHO：improved Spotted Hyena Optimization Algorithm for Phishing Website Detection［J］. Multimedia Tools and Applications， 2022， 81：34677-34696.

［24］ 戴天虹， 孙春雪， 黄建平， 等. 基于黄金正弦混沌斑鬣狗优化算法的高光谱波段选择［J］. 激光与光电子学进展， 2022， 59（10）：519-528.

DAI Tianhong， SUN Chunxue， HUANG Jianping， et al. Hyperspectral Wave Band Selection Based on Golden Sine and Chaotic Spotted Hyena Optimizer Algorithm［J］. Progress in Laser Light And Optoelectronics， 2022， 59（10）：519-528.

［25］ 汪定伟， 王俊伟， 王洪峰， 等. 智能优化方法［M］. 北京：高等教育出版社， 2007.

WANG Dingwei， WANG Junwei， WANG Hongfeng， et al. Intelligent Optimization Method［M］. Beijing：Higher Education Press， 2007.

［26］ 陈贵敏， 贾建援， 韩琪. 粒子群优化算法的惯性权值递减策略研究［J］. 西安交通大学学报， 2006， 40（1）：53-56.

CHEN Guimin， JIA Jianyuan， HAN Qi. Study on the Strategy of Decreasing Inertia Weight in Particle Swarm Optimization Algorithm［J］. Journal of Xian Jiaotong University， 2006， 40（1）：53-56.