矩形管辊弯成形角部充满度分析及试验验证

邢梦龙 杜凤山 付玉涛

摘要：为了提高矩形管辊弯成形角部的成形精度，根据体积不变定律和金属秒流量相等原则对矩形管角部欠充满原因进行分析；结合工廠实际生产参数建立辊弯成形有限元模型，分析圆管管径和壁厚对成形过程中增厚系数、角部充满度的影响；根据角部欠充满区域中性层弧长线性对应关系进行圆管管径修正，确定系数修正关系式；对角部成形过程进行损伤判定，筛选出合适的圆管管径，将其仿真结果与试验进行对比。结果表明：辊弯成形过程中壁厚的增大使得角部处于欠充满状态；壁厚越小，成形过程中的增厚系数越小，所需圆管管径越小；圆管管径越大，角部充满度越好，同时管径的增大会增加辊弯出口处角部内侧损伤的可能性；仿真与试验结果的误差较小，验证了仿真模型的准确性。

关键词：辊弯成形；角部充满度；系数修正；角部损伤

中图分类号：TG306

DOI：10.3969/j.issn.1004132X.2023.07.013

Analysis and Experimental Verification of Corner Filling Degree of

Rectangular Tube Roll Forming

XING Menglong1 DU Fengshan1 FU Yutao2

1.National Cold Rolling Strip Equipment and Process Engineering Technology Research Center of

Yanshan University，Qinhuangdao，Hebei，066004

2.Qinhuangdao Chen-Ming Special-shaped Pipe Manufacturing Co.，Ltd.，Qinhuangdao，Hebei，066000

Abstract： In order to improve the forming accuracy of square rectangular tube corners formed by roller forming， the causes of underfilling rectangular tube corners were analyzed according to the law of constant volume and the principle of equal metal flow per second. The finite element model of roll forming was established according to the actual production parameters in the factories， and the influences of pipe diameter and wall thickness on the thickening coefficient and corner filling degree in the forming processes were analyzed. According to the linear relation of arc length of neutral layer in underfilled regions of the corner， the tube diameter was corrected and the coefficient correction relation was determined. The damage of the corner forming processes was judged， and the appropriate diameter of the round pipe was selected. The simulation results were compared with the experimental ones. The results show that the corners are underfilled with the increase of wall thickness during roll forming. The decrease of wall thickness leads to the decrease of thickening coefficient， and the required diameters of circular pipes are smaller. With the increase of pipe diameters， the corner filling degree is better， at the same time， the increase of pipe diameters will increase the possibility of damage in the inner corner at the exit of roll forming. The errors between the test results and the experimental results are small， which verifies the accuracy of the simulation model.

Key words： roll forming； corner filling degree； coefficient modification； corner damage

0 引言

辊弯成形的断面钢材广泛应用于建筑、汽车、交通运输、石油化工等领域［1］。连续辊弯成形是将板带或管材通过辊弯机成形输出各种异型管的工艺。辊弯成形根据原材料几何类型的不同，可以分为开式辊弯成形和闭式辊弯成形。其中，圆管成形方矩形管为闭式辊弯成形，优点是产品质量更好，机组成形速度更快，效率更高，所以得到了更广泛的应用。

在闭式辊弯成形的相关研究中，NAGAMACHI等［2-3］通过仿真与试验研究了立辊偏置成形对方管角部充满度的影响，并对方管管端变形进行了分析。ABRINI等［4］和FARAHMAND等［5］根据辊弯过程中的金属流动规则，对管坯的变形区和自由区进行划分，基于上限法推导了辊弯过程的解析解，并结合试验验证了解析模型的准确性。BAYOUMI［6-7］给出了圆管冷拔正多边形管的解析解，研究了截面形状、摩擦因数对力能参数的影响，并通过与试验结果及有限元模拟对比，验证了解析模型的准确性，该方案可应用于低碳钢标准圆管。LEU等［8］基于更新的拉格朗日弹塑性有限元模型研究了多因素对圆管缩方过程中不对称程度的影响。HOSSEINZADEH 等［9］基于有限元法（FEM）和响应面法（RMS）对方管拉拔工艺参数进行了优化，通过与有限元结果对比可知，该方法能够高度预测最优工艺参数组合。YAO 等［10-12］基于有限元法提出了一种预测残余应力和等效塑性应变的方法，通过获得不同参数的数据建立了残余应力和等效塑性应变的解析模型。彭雪锋等［13］对高强钢方管角部进行在线感应加热，并对不同温度角部内侧裂纹的演化进行了研究。韩飞等［14］对不同材料和厚度的方管进行不同部位的取样，通过拉伸测试发现R角区域的屈服强度大于平面区域；曾国等［15］对辊弯方矩形管采用X射线衍射的方法对其内外表面进行了残余应力的测试，发现采用圆成方的纵向残余应力水平比采用方成方的残余应力大；徐树成等［16-17］采用三维大变形弹塑性有限元法，考虑材料和几何的非线性，描述了圆管成形方矩形管的非稳定轧制到稳定轧制的过程；杜凤山等［18-20］采用三维大变形理论模拟了四辊辊弯成形过程，并对管壁壁厚进行了研究。

尽管大多数学者都对闭式辊弯过程金属流动进行了研究，但在圆管辊弯成形方矩形管过程中会出现管壁增厚现象［21］，尤其是角部更加明显。本文基于体积不变定律和金属秒流量相等原则对圆管辊弯成形方矩形管过程中的参数变化进行分析，建立辊弯成形有限元模型，分析圆管管径和壁厚对辊弯过程中增厚系数和角部充满度的影响，基于角部欠充满状态，根据角部中性层弧长对圆管管径进行系数修正，并对可能存在的角部损伤问题进行损伤判定，对确定的圆管管径进行辊弯试验，将仿真结果与试验进行对比，验证了仿真模型的準确性。

1 理论方法

1.1 体积不变定律

在圆管辊弯成形方矩形管过程中满足体积不变定律［22］：

式中，K为总扩展系数；S0为圆管截面面积；Sn为矩形管截面面积；tn为方矩形管壁厚；t0为圆管壁厚；μ为延伸系数；ε为增厚系数。

在孔型设计中，ε=1，即K=μ，但在实际生产中，由于金属的流动tn会出现不同程度的增大，从而导致辊弯成形后Sn增大，容易造成角部处于欠充满状态。

1.2 金属秒流量相等原则

在辊弯成形过程中，轧辊整体由一台电机驱动，各个道次轧辊角速度相同，假设机架间满足金属秒流量相等原则［22］：

式中，Rn为轧辊最后变形道次平均半径；R0为轧辊第一次变形道次平均半径；δ为平均延伸系数。

理论上δ=μ为常数，但在实际生产中，由于轧辊孔型上接触点的变化使得质点速度不同，δ会产生变化，δ的变化会产生一定的张力来保持辊弯成形的稳定。

1.3 辊弯成形参数变化分析

由于在实际生产过程中存在管壁增厚的现象，同时角部容易处于欠充满状态，故需要考虑增大圆管管径对角部进行补偿填充，但这样又会导致壁厚的继续增大，即圆管管径的增大一部分用于纵向延伸，一部分用于管壁的增厚，其中参数变化如表1所示。

2 有限元仿真

2.1 有限元建模

图1为闭式辊弯成形示意图，其中第一道次为定径道次不参与变形，从第二道次开始进行压下分配，经过多道次辊弯成形后输出异型管。

对图1过程进行有限元建模来分析增厚系数分布及角部充满度情况，结合工厂生产的40 mm×27.5 mm×3 mmSUS304不锈钢矩形管，在MSC.MARC中根据辊花图建立辊弯成形仿真模型，由于成形具有对称性，所以采用1/4有限元模型，如图2所示。

圆管管径根据孔型设计计算获取。对圆管角部成形区域进行网格细化，其中平辊为驱动辊，立辊为从动辊，各个道次角速度相同均为1 rad/s，平辊摩擦因数为0.2，立辊摩擦因数为0.001。由于第一道次不参与变形，所以模型从第二道次开始建立，第二道次变形轧辊直径为160 mm，最后道次轧辊直径为164 mm，中间道次中后一个道次比前一个道次按比例逐渐递增。咬入阶段由推板将圆管推入孔型，咬入后撤去推板，根据金属秒流量相等原则推板的速度为79.7 mm/s。

在材料模型中，弹性阶段设定泊松比为0.3，弹性模量为210 GPa；塑性阶段流动应力采用Swift模型对SUS304不锈钢进行拟合，如图3所示，可以看出试验结果与流动模型拟合度较高，能够应用于仿真模型中。

2.2 仿真结果分析

根据辊花图计算圆管外半径为20.87 mm，设计孔型与仿真结果对比如图4所示。可以看出：外表面长边与短边重合度很高，内表面存在一定的内移，说明管壁的增厚是通过内壁的内移实现的，这是因为外表面由于轧辊的限制作用，导致金属只有通过向内流动实现管壁的增厚；在角部成形方面，内侧与外侧均出现了欠充满的现象，且存在一定误差，其中金属在内侧及外侧剪应力矢量分布如图5所示。根据变形区（Ⅰ区）可以看出，角部内侧剪应力整体高于外侧，内侧剪应力在角部与长短边过渡区域附近最高，由于金属的流动阻力造成了金属堆积；同时根据角部外侧剪应力分布可知，角部外侧处于向角部填充状态，从而引起了角部增厚，随着成形的结束（图中Ⅱ区和Ⅲ区）剪应力逐渐减小，并逐渐改变方向，趋向于残余应力分布，即外拉内压［15］。根据体积不变定律可知平衡增厚系数与角部充满度对矩形管成形有着至关重要的影响。

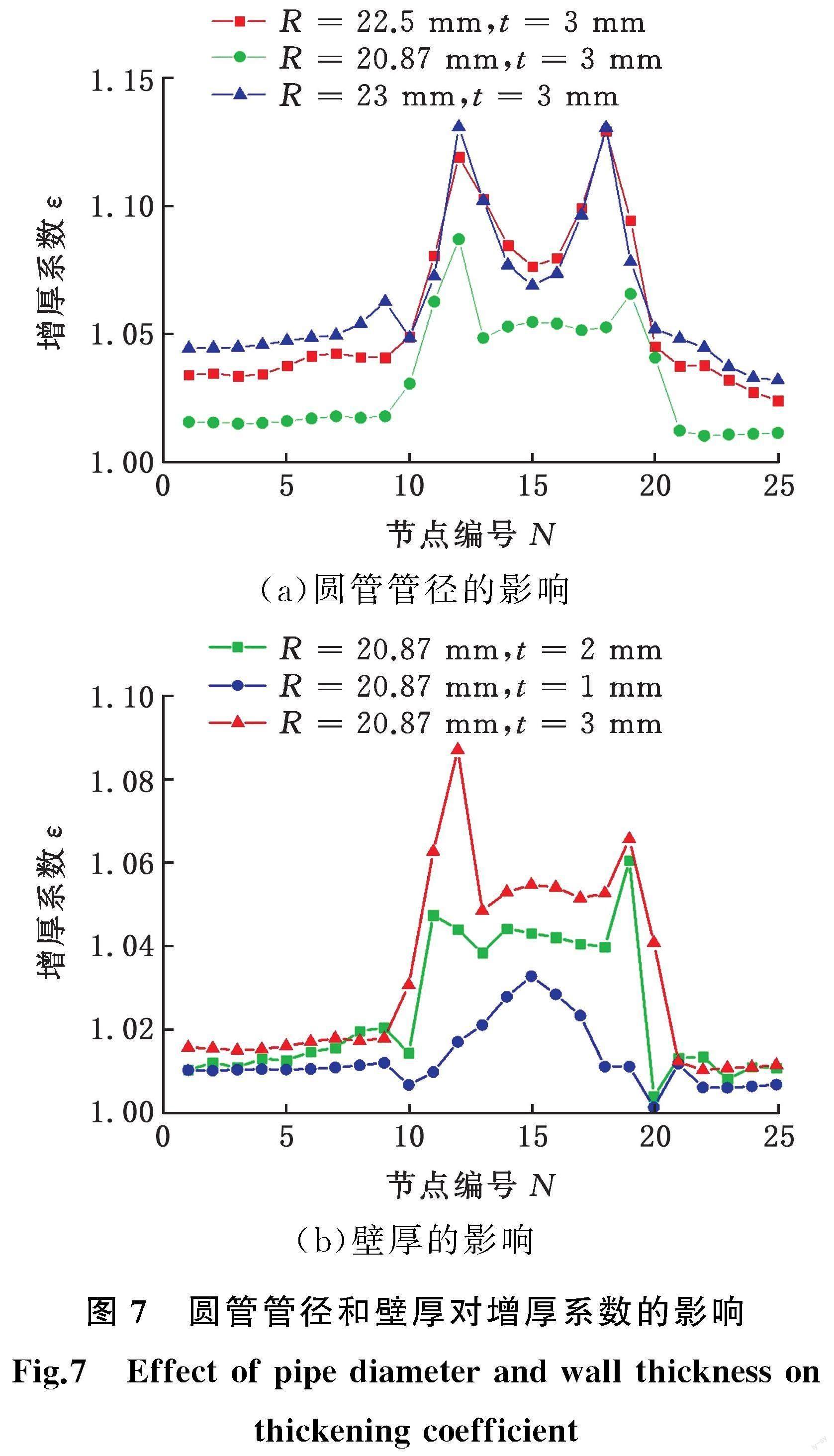
2.3 圆管半径和厚度对增厚系数的影响

对1/4圆管网格节点进行编号，如图6所示，分别采用圆管壁厚为1，2，3 mm和圆管外半径R为20.87，22，22.5 mm进行仿真模拟，在保持40 mm×27.5 mm×3 mm矩形管孔型不变的前提下，分析厚度为3 mm不同圆管管径对增厚系数的影响。由图7a可以看出，随着管径的增大，增厚系数也呈现增大趋势，在节点编号12和18附近增厚系数最大。这是因为角部处于自由成形区，角部与长边及短边交界区域金属流动剧烈，但由于管壁相对较厚，阻碍了其金属流动，便在该区域堆积，造成增厚。分析在相同圆管管径下不同厚度对增厚系数的影响，如图7b所示。可以看出，随着厚度的增大，增厚系数逐渐增大，但当t=1 mm时，增厚系数变化不大，最大增厚系数出现在节点编号15附近，此时管壁厚度较小，阻碍金属流动的能力变弱，造成了15号节点附近金属堆积，这与图5的剪应力矢量分布情况一致。

2.4 圆管半径和厚度对充满度的影响

图8所示为圆管半径和壁厚对角部充满度的影响，可以看出，在厚度t为3 mm时，采用圆管外半径R=22.5 mm效果较好，R=20.87 mm和R=22 mm时角部处于欠充满状态；当厚度为2 mm时，采用R=22 mm效果较好，R=22.5 mm时会使角部处于过充状态，R=20.87 mm时出现欠充满；当厚度为1 mm时，采用R=22.5 mm和R=22 mm时会出现角部过充满的情况，R=20.87 mm时效果较好。可以看出在同一种孔型下，不同厚度应匹配不同圆管管径。

3 线性补偿与损伤判定

3.1 圆管的线性补偿

理论上，延伸系数应根据式（2）选取，但由于孔型上每个质点的速度不同以及张力的作用，所以一般取值为1.02～1.04之间，由于辊弯过程中壁厚的增加及角部的欠充满状态，所以需要根据角部区域中性层弧长对圆管进行系数修正，以补偿角部欠充满区域。

以40 mm×27.5 mm×3 mm的矩形管孔型为例，设计圆管外半径为20.87mm，根据图4角部欠充满状态进行补偿计算，对设计孔型与仿真孔型进行系数修正。充满度采用成形后角部平均弧长与设计平均弧长比值作为评价指标，即

式中，C3、C1分别为成形后角部区域内侧、外侧弧长；C2、C4分别为设计角部区域外侧、内侧弧长。

补偿量计算如下：

式中，yc為1/4段圆管对应补偿量。

系数修正后圆管外半径为

式中，γ为修正系数；t-n为矩形管平均壁厚；Cn为圆管中性层长度。

γ=1时，计算结果如表2所示。

3.2 角部内侧损伤判定

由有限元结果可知，在矩形管角部区域内侧出现了应力集中，增加圆管管径进行补偿的同时会增加角部内侧损伤的可能性，所以采用全解耦的韧性损伤准则作为判定依据对角部区域进行损伤倾向判定。

应力三轴度定义为

式中，σm为静水压力；σe为等效应力；σ1为第一主应力，即最大主应力；σ2为第二主应力；σ3为第三主应力。

根据应力三轴度的大小采用LeRoy准则和Oh准则分别进行损伤判定。LeRoy准则能够准确预测低应力三轴度下的损伤，其定义为

式中，εf为断裂应变；εp为等效塑性应变；C为断裂阈值。

采用剪切缺口试样对LeRoy准则进行标定，损伤区域进行局部网格加密，具体标定结果如图9所示。为了更好地说明辊弯过程中角部损伤位置，取圆管R=22.5 mm，建立辊弯损伤模型，对其角部及圆管尾部进行网格加密。在MSC.MARC中采用PLOTV子程序输出应力三轴度和LODE角参数，损伤值可以采用PLOTV或UDAMAGE_INDICATOR进行输出。由于两种方法迭代计算方式不同，会产生一定的偏差，本文采用计算结果偏保守的PLOTV子程序，在子程序中三个主应力需要根据应力分量进行转换计算求得。损伤值计算

结果如图10a所示，可以看出其损伤值未达到损伤阈值，初步判定不会发生损伤。但在实际成形过程中，产品需要在成形截面尺寸满足要求的情况下，确保角部不发生损伤，由于成形时角部复杂的应力状态、角部成形时的塑性变化以及准则标定误差，所以需要考虑一个合理的“安全因子”进行评价。采用工程应变作为“安全因子”进行损伤判定，结果如图10b所示，可以看出辊弯结束状态角部内侧损伤值超过损伤阈值，即图10b中A区域，此时应力三轴度处于低水平，LODE角参数θ-在［-1，1］区间内的分布情况如图10b所示，可以判断该区域为危险区域。

Oh准则对高应力三轴度和负应力三轴度的预测结果较好［23］，所以采用Oh准则对高应力三轴度和负应力三轴度区域进行损伤判定，表达式为

采用圆角缺口试样对Oh准则进行标定，同样在损伤区域进行局部网格加密，标定结果如图11所示。取圆管R=22.5 mm进行辊弯仿真，损伤值分布如图12a所示，可以看出仿真结果未达到损伤阈值，初步判定不发生损伤。采用工程应变的计算结果如图12b所示，当应力三轴度小于-1/3时，认定断裂应变为无穷大，即材料永远不会发生韧性断裂［24］，可以看出在负应力三轴度条件下，会出现少量的损伤区域。综上，角部的损伤区域处于低应力三轴度或负应力三轴度状态。

由图8可以看出，采用圆管R=22.5 mm、t=3 mm时辊弯成形角部充满度较好，但在工程应变的预测下，角部内侧存在损伤危险区域，故不能采用。采用圆管R=22 mm时，提取工程应变计算结果，如图13所示，由角部内侧损伤云图可以看出，在低应力三轴度下，未出现损伤区域，但在负应力三轴度下，仍然存在少部分的区域超过损伤阈值，故不能采用。图14所示为R=21.5 mm时，在工程应变条件下LeRoy准则和Oh准则的损伤值分布，可以看出并未超过损伤阈值。由于在R=22.5 mm时采用张量应变计算损伤值是安全的，所以当R=22 mm和R=21.5 mm时采用张量应变计算也不会发生损伤，即当R=21.5 mm时，采用张量应变和工程应变计算都满足损伤判据，所以采用R=21.5 mm可行。同时，根据GB/T6728—2002可知，采用R=22.5 mm和R=23 mm时，在金属堆积节点位置会出现壁厚超差的情况（图7）；采用R=21.5 mm时满足壁厚偏差要求及R角要求。

4 试验验证

采用修正后圆管外半径21.5 mm进行40 mm×27.5 mm×3 mm的SUS304不锈钢矩形管辊弯成形试验。将矩形管的仿真、试验、设计结果进行对比，由图15可以看出，在外表面，长边与短边仿真结果、设计结果与试验结果吻合度很高；在内表面，长边与短边出现了一定程度的内移，导致壁厚出现少量增加，仿真、设计结果与试验结果吻合度较高；在角部区域，外表面与内表面均出现了欠充满现象，同时厚度增加明显，仿真结果与试验结果吻合度较高，但与设计结果存在一定差距，在可接受范围内。这与上述分析结果一致，从而验证了仿真模型的准确性。辊弯圆管管径尺寸整体确定具体流程如图16所示。

5 结论

本文根据体积不变定律和金属秒流量相等原则对圆管辊弯成形方矩形管进行了参数分析，针对40 mm×27.5 mm×3 mm的SUS304不锈钢矩形管建立了辊弯成形有限元模型，分析了管径和壁厚对增厚系数和角部充满度的影响。根据线性对应关系对圆管管径进行了系数修正，并基于韧性损伤准则对角部内侧可能出现的损伤区域进行判定，将确定的圆管仿真结果与试验结果进行了对比，得到以下结论：

（1）圆管成形方矩形管过程中由于内侧无约束存在，外侧受到轧辊的限制，会使金属沿壁厚方向产生流动，使得管壁厚度增加，厚度的增加會使方矩形管角部处于欠充满状态。

（2）通过增加圆管管径能够有效缓解角部欠充满问题，但管径的增加会使壁厚再次增大，同时角部内侧区域在辊弯成形结束阶段发生金属堆积，有引起角部损伤的可能。

（3）在工程应变条件下，采用R≥22 mm的圆管在辊弯结束阶段会在角部内侧出现低应力三轴度或负应力三轴度的损伤；采用R=21.5 mm圆管的试验与仿真结果吻合度较高，但与设计结果存在一定差距，在可接受范围内，验证了有限元模型的准确性。

参考文献：

［1］ HALMOS G T. Roll Forming Handbook［M］. Boca Raton：CRC Press，2006：2-5.

［2］ NAGAMACHI T， NAKAKO T， NAKAMURA D. Effects of Forming Conditions of Roll Offset Method on Sectional Shape at the Corner of Square Steel Pipe［J］. Materials Transactions， 2013， 54：1703-1708.

［3］ NAGAMACHI T， NAKAKO T， NAKAMURA D. Mechanism of Pipe End Deformation after Cutting of Square Steel Pipe Formed by Roll Forming［J］. Materials Transactions， 2013， 54：1910-1915.

［4］ ABRINI K， FARAHMAND H R. An Upper Bound Analysis for the Reshaping of Thick Tubes with Experimental Verification［J］. International Journal of Mechanical Sciences， 2008，50：342-358.

［5］ FARAHMAND H R， ABRINI K. An Upper Bound Analysis for Reshaping Thick Tubes to Polygonal Cross-section Tubes through Multistage Roll Forming Process［J］. International Journal of Mechanical Sciences， 2015，100：90-98.

［6］ BAYOUMI L S. Cold Drawing of Regular Polygonal Tubular Sections from Round Tubes［J］. International Journal of Mechanical Sciences， 2001，43：2541-2553.

［7］ BAYOUMI L S. Analysis of Flow and Stresses in Flattening a Circular Tube by Rolling［J］. Journal of Materials Processing Technology， 2002， 128：130-135.

［8］ LEU D K， WU J Y. Finite Element Simulation of the Squaring of Circular Tube［J］. International Journal of Advanced Manufacturing Technology， 2005， 25：691-699.

［9］ HOSSEINZADEH M， MOUZIRAJI M G. An Analysis of Tube Drawing Process Used to Produce Squared Sections from Round Tubes through FE Simulation and Response Surface Methodology［J］.International Journal of Advanced Manufacturing Technology， 2016，87：2179-2194.

［10］ YAO Y， QUACH W M， YOUNG B. Finite Element-based Method for Residual Stresses in Cold-formed Steel Hollow Sections［J］. Engineering Structures， 2019， 188：24-42.

［11］ YAO Y， QUACH W M， YOUNG B. Cross-section Behavior of Cold-formed Steel Elliptical Hollow Sections—a Numerical Study［J］. Engineering Structures， 2019，201：109797.

［12］ YAO Y， QUACH W M， YOUNG B. Simplified Models for Residual Stresses and Equivalent Plastic Strains in Cold-formed Steel Elliptical Hollow Sections［J］. Thin-Walled Structures，2020，154：106835.

［13］ 彭雪锋，陈强，王宇，等.局部感应加热对高强钢方管二次辊压成形的影响［J］.工程科学学报，2016，38（7）：973-978.

PENG Xuefeng， CHEN Qiang， WANG Yu， et al. Effect of Local Induction Heating on Secondary Roll-forming of High Strength Square Tubes［J］. Chinese Journal of Engineering， 2016，38（7）：973-978.

［14］ 韩飞，张涛.中厚壁方管冷弯成形效应研究［J］. 焊管，2016，39（7）：61-64.

HAN Fei， ZHANG Tao. Experimental Investigation on Cold-forming Effect of Middle Thick-walled Square Tube［J］. Welded Pipe and Pipe， 2016，39（7）：61-64.

［15］ 曾国，郭永进，于忠奇，等.辊弯成形方形型钢的残余应力［J］. 钢铁研究学报，2008，20（11）：29-32.

ZENG Guo， GUO Yongjin， YU Zhongqi， et al. Residual Stresses of Roll-formed Shape with Square Section［J］. Journal of Iron and Steel Research， 2008，20（11）：29-32.

［16］ 徐树成，刘才.方矩形管第一道次辊弯成形过程的变形和应力场［J］. 燕山大学学报，2000，24（1）：15-18.

XU Shucheng， LIU Cai. The Deformation and Stress Field for Square Rectangle Tube Roll Forming Process in First Pass［J］. Journal of Yanshan University， 2000，24（1）：15-18.

［17］ 徐树成，刘才.方矩形管连续辊弯成形过程的变形和应力场［J］. 机械工程学报，2000，36（3）：93-96.

XU Shucheng， LIU Cai. Deformation and Stress Field of Square Rectangle Tube in Continue Roll Forming Process［J］. Chinese Journal of Mechanical Engineering， 2000，36（3）：93-96.

［18］ 杜凤山，陆卫平，张建宇，等.方管闭式辊弯成形过程的变形及流场［J］. 东北重型机械学院学报，1997，21（2）：100-103.

DU Fengshan，LU Weiping，ZHANG Jianyu， et al. Deformation and Flow Fields of the Square Tube Forming of 4-roll Bending［J］. Journal of Northeast Heavy Machinery Institute， 1997，21（2）：100-103.

［19］ 杜鳳山，付志强，于辉.矩形管冷弯成形的辊花设计及成形规律［J］. 中国机械工程，2016，27（21）：2841-2845.

DU Fengshan，FU Zhiqiang，YU Hui．Roll Flower Design and Forming Mechanism of Rectangular Pipes in Cold Roll Forming Processes［J］. China Mechanical Engineering， 2016，27（21）：2841-2845.

［20］ 付志强，安子军，杜凤山，等.方矩形管连续辊弯成形延伸规律［J］. 吉林大学学报（工学版），2015， 45（2）：487-493.

FU Zhiqiang， AN Zijun， DU Fengshan， et al. Elongation of Rectangular Tube in Continuous Roll Forming［J］. Journal of Jilin University （Engineering and Technology Edition）， 2015， 45（2）：487-493.

［21］ 曹国富，卢启威.方矩管管壁增厚的原因分析［J］. 焊管，2010，33（7）：55-59.

CAO Guofu， LU Qiwei. Discussion on Thickening Reason of Rectangular Pipe Wall Thickness［J］. Welded Pipe and Tube， 2010，33（7）：55-59.

［22］ 杜凤山，邢梦龙，裴新元，等.一种考虑增厚系数的圆管成型方矩形管孔型设计方法：CN， 202110057360.5［P］. 2022-03-15.

DU Fengshan，XING Menglong，PEI Xinyuan，et al. Circular Tube Forming Square Rectangular Tube Pass Design Method Based on Thickening Coefficient：CN，202110057360.5［P］. 2022-03-15.

［23］ MA H， XU W C，JIN B C， et al. Damage Evaluation in Tube Spinnability Test with Ductile Fracture Criteria［J］. International Journal of Mechanical Sciences， 2015，100：99-111.

［24］ BAO Y B， WIERZBICKI T. On the Cut-off Value of Negative Triaxiality for Fracture［J］. Engineering Fracture Mechanics， 2005， 72：1049-1069.